PSSN在TM T宽视场光谱仪中的应用研究∗

陈力斯 胡中文

(1中国科学院国家天文台/南京天文光学技术研究所 南京 210042) (2中国科学院天文光学技术重点实验室 南京 210042) (3中国科学院大学 北京 100049)

PSSN在TM T宽视场光谱仪中的应用研究∗

陈力斯1,2,3†胡中文1,2

(1中国科学院国家天文台/南京天文光学技术研究所 南京 210042) (2中国科学院天文光学技术重点实验室 南京 210042) (3中国科学院大学 北京 100049)

光学系统像质评价是光学设计的核心,通过对常用像质评价方法与在30m望远镜(Thirty M eter Telescope,TMT)的像质评价中提出的归一化点源灵敏度函数(Norm alized Point Source Sensitivity,PSSN)的分析比较,对PSSN在TM T宽视场光谱仪(W ide Field Optical Spectrom eter,W FOS)中的应用进行了研究.包括对大气视宁度的简化模拟、TM T中M 3的移动对系统PSSN的影响、W FOS中准直镜的移动对系统PSSN的影响、在不同大气湍流的条件下PSSN与天顶角的关系以及PSSN与波像差的均方根值(root m ean square of wavefront error,RMSW FE)µ之间的关系.结果表明,PSSN对视宁度受限下的TMT的像质评价是有效的.

望远镜,像质评价,方法：数值

1 光学系统像质评价概述

所有的像质评价方法,都可以归结为基于几何光学的方法和基于衍射理论的方法.点列图是由一点发出的多条光线经过光学系统成像后,由于像差的存在,在像面不再集中于一点,而是形成一个弥散图形.它的优点是直观、易算,但用它来评价像质,在很多场合下与实际情况并不符合.光学系统的分辨率是指能被光学系统分辨开的两个物点(或像点)之间的最小距离.它反映了光学系统分辨物体细微结构的能力.分辨率和点列图方法,主要考虑像差对成像质量的影响,仅仅适用于大像差系统,不适用于小像差系统[1].

瑞利判断是实际波面与参考球面波之间的最大波像差不超过λ/4时,此波面是无缺陷的.瑞利判断是一种较为严格的像质评价方法,便于实际应用,适用于小像差光学系统,但瑞利判断是不够严密的,它只考虑了波像差的最大值,而未考虑波面上缺陷部分在整个面积中所占的比重.中心点亮度是指光学系统存在像差时,其成像衍射斑的中心亮度和不存在像差时衍射斑的中心亮度之比SD.斯托列尔准则是当SD≥0.8,认为光学系统的成像质量是完善的.斯托列尔准则是一种高质量的像质评价标准,适用于小像差光学系统,但是由于其计算复杂,很少作为评价方法使用[2].

物体经光学系统成像,其传递结果是物体的空间频率不变,像体的频率发生平移.光学传递函数是以空间频率为变量,表征成像过程中调制度和横向相移的相对变化的函数.光学传递函数同时适用于大像差系统和小像差系统,但它仅仅考虑对物体不同频率成分的传递能力,不能全面评价成像系统的性能[1].

专门针对TMT视宁度受限提出的PSSN反映了望远镜的科学效率,刻画了在望远镜的观测时间内能量的损失[3].PSSN最重要的特性是可乘性,即全部误差共同存在于系统时系统的PSSN等于各个误差单独存在于系统时系统PSSN的乘积[4].

2 归一化的点源灵敏度函数PSSN

2.1 PSSN的定义[3]

PSSN的定义为:

由于光学传递函数OTF(Optical Transfer Function)是PSF的傅里叶变换[4],根据Parseval能量定理,有[5]

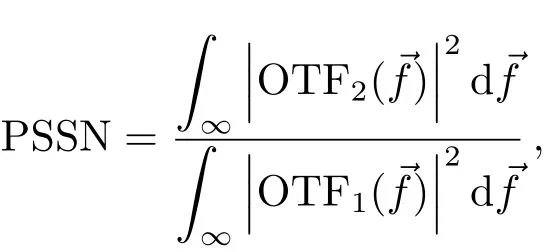
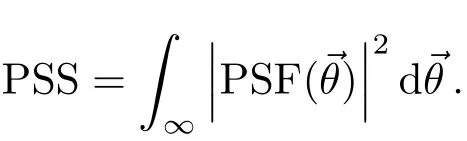
PSSN有如下性质[5]:

(1)0≤PSSN≤1;

(2)对于低频和小像差的望远镜系统,系统的PSSN具有可乘性.若一个系统中存在n个误差e1,e2,···,en,它们单独存在时,系统的PSSN分别为PSSN1,PSSN2,···, PSSNn.它们同时存在于一个系统中时系统的PSSN为pssn,有

2.2 PSSN与其他像质评价方法的关系

(1)在波像差很小时,PSSN与波像差的均方根值µ存在如下关系：

其中α是一个常数,是波长λ、光程差OPD(Optical Path Difference)和Fried参数r0的函数.事实上,µ很小时,有[5]

(2)当相差的性质近似是白噪声时,PSSN与Streh l比率σ的关系为[5]:

(3)PSSN与中心点亮度CIR(Central Intensity Ratio)的关系为[5]

3 PSSN在W FOS中的应用

3.1 TM T和W FOS光学系统简介

TMT是一台RC(Ritchey-Chretien)式光学望远镜.如图1所示,其主镜M 1和副镜M 2均为双曲面.三镜M 3将来自副镜M 2的光线反射至观测所用的科学仪器中.M 1口径30m;M 2口径3.1m;M 3是椭圆形的平面镜,M 3的有效通光口径长轴为3500mm,短轴为2450mm,机械尺寸大小为3594mm×2536mm.材料选用低膨胀系数的微晶玻璃.

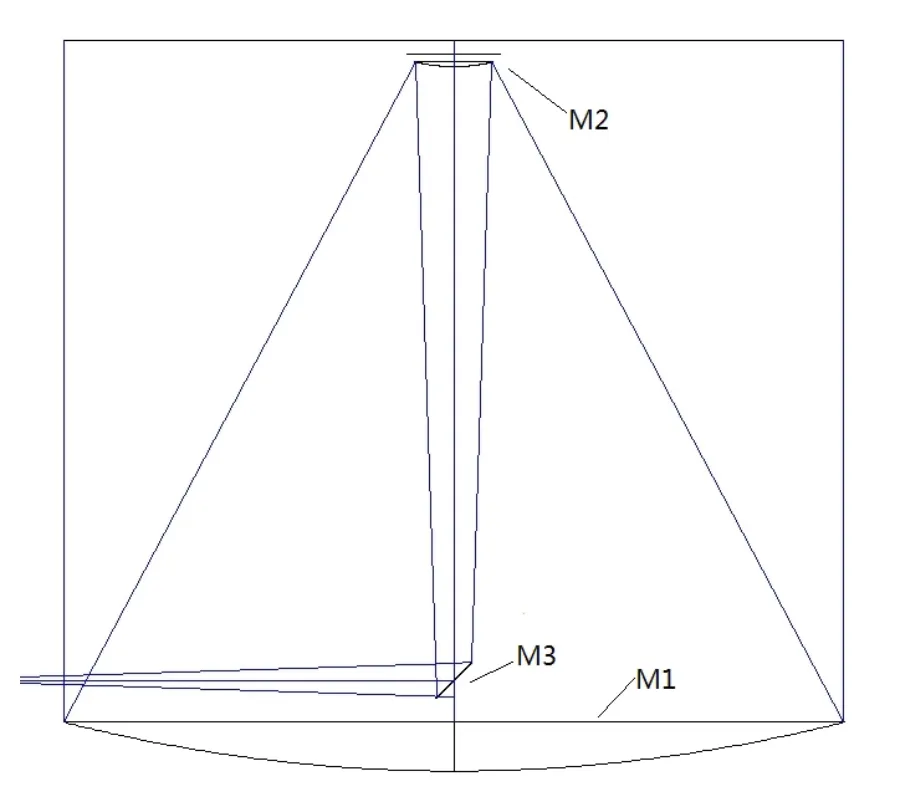
图1 TM T中M 1、M 2、M 3Fig.1 M 1,M 2,and M 3 o f TM T

WFOS是工作在视宁度受限的成像光谱仪,如图2所示,它可用于0.31–1.0µm的全光学波段对暗弱天体进行多目标光谱观测、单目标光谱观测或者直接成像观测.图中,dia.代表直径(diameter),Disp.代表色散(dispersion),GEX是光栅切换系统.规划中的W FOS光束口径300mm,采用分色镜具有红区和蓝区两个相机,可一次曝光覆盖整个波长范围.

本文首先对大气湍流进行了近似模拟,利用模拟的大气,在Zemax软件和M atlab中仿真计算各种情况下系统的PSSN.

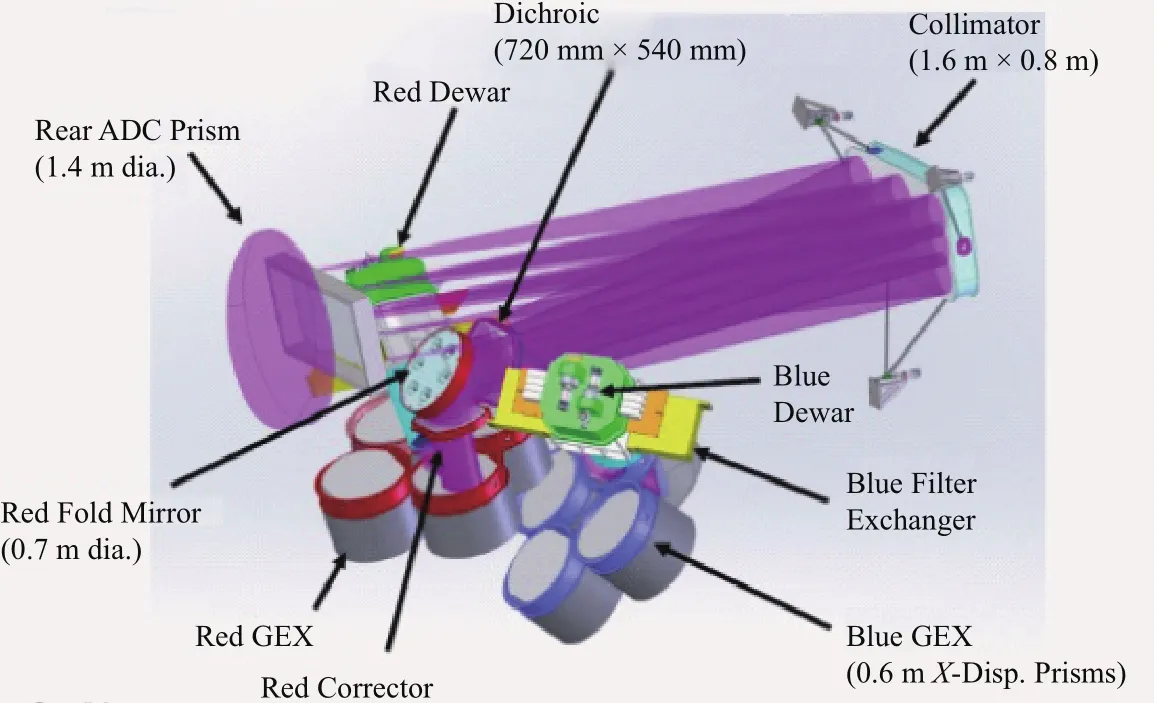
图2 W FOS的结构1h ttp://www.tm t.org/Fig.2 The structu re o f W FOS1

3.2 大气视宁度的近似模拟

大气湍流对光学波前的影响可以用Zernike模式分析,由于Zernike模式并非统计独立,Roddier通过Zernike模式的加权构造了统计独立的Karhunen-Loeve(简称K-L)函数[6].本文先用K-L函数构造随机波前[7],通过K-L函数可以将随机波前展开为Zernike多项式的形式.然后在Zemax软件中,不断调整Zernike系数,用Zernike面模拟视宁度是1′′的大气.

受大气湍流(这里指弱湍流)影响的光学波前可以分解为Zernike多项式的形式,即:

式中Zj(r)为Zernike多项式各项,aj为加权系数.大气波前的Zernike系数ap可以认为是具有零均值的Gauss随机变量,考虑展开成有限项Zernike多项式,记:

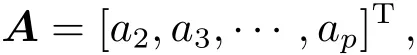
其协方差阵为

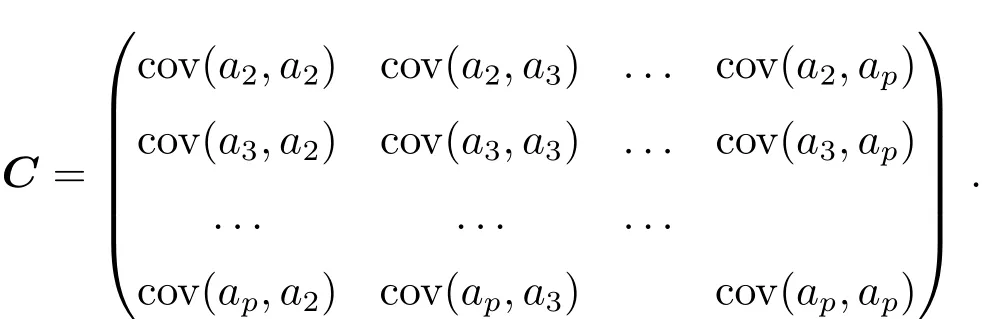
Noll从能量的角度考虑,推导出任意两项Zernike系数的协方差表达式[8],因此我们可以看出C为对称矩阵.Zernike系数之间存在一定协方差,即Zernike多项式并不是统计独立.

为产生湍流随机波前,利用K-L函数,波前展开为:

系数bj是统计独立的随机量,即其协方差矩阵是对角矩阵,Kj(r)为K-L函数各项. Kj(r)是Zernike多项式各项的线性组合,有

考虑展开成有限项多项式,记

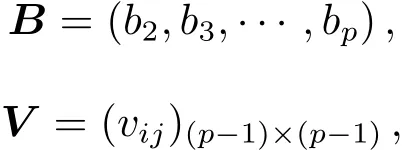
其中矩阵B的元素是(6)式各项的系数,矩阵V的元素是(7)式各项的系数,有A=B V.

考虑到矩阵C,由矩阵理论可知,存在一酉阵U,使得

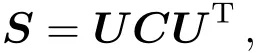
其中S为对角阵.S中的元素是各个Zernike系数的方差.

取V=U−1,根据(6)式可以得到K-L函数的各项.生成p−1个具有零均值且方差由对角阵S给出的Gauss随机变量,这些随机变量就是K-L函数的系数B.由关系A= V B=U−1B,我们可以得到仿真波前的Zernike系数A.

K-L函数的不足之处是没有统一的解析表达式,通过对Zernike多项式各项的线性组合,使得随机波前展开成K-L函数的各项系数统计独立.

对于视宁度是1′′的大气,一束平行光通过大气后,通过一个焦距为f=100mm的理想透镜,在该理想透镜焦平面上得到光斑大小为d,有

解得d=0.48µm.

在Zemax软件中,用K-L函数构造随机波前得到的Zernike系数构成Zernike面,在其后方加入一个焦距为100mm的理想透镜,通过不断调节Zernike系数,使理想透镜焦平面上得到的光斑大小接近0.48µm,得到各项的Zernike系数如表1.本文使用上述Zernike系数作为对大气湍流的模拟.

表1 大气视宁度近似模拟的Zernike系数Tab le 1 The Zern ike coefficien ts o f atm osp heric seeing in an ap p rox im ate sim u lation

3.3 PSSN的应用[9−11]

3.3.1 M 3的移动对系统PSSN的影响

对TMT官方提供的文件名为130819v286-red-imaging.zmx的文件,在光瞳面前加入Zernike面,Zernike系数由3.2节的方法获得.天顶角为25°,考虑M 3的误差对系统PSSN的影响[3,5].

计算有像差情况下的PSS

理想情况下PSS

对波长λ=0.3µm,天顶角为25°的情况,在Zemax软件中导出PSF图形如图3.

在Zem ax软件中，导出PSF的矩阵,应用如下公式,

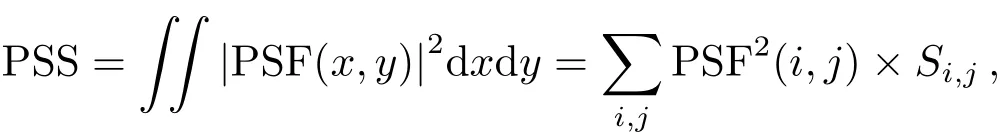
其中Si.j为第i行第j列矩形的面积,分别求得有误差和没有误差情况下的PSS.根据公式

当X方向倾斜XTilt=0°、Y方向倾斜YTilt=0°、Z方向倾斜ZTilt=0°时,X方向离轴XDecenter=0mm、Y方向离轴YDecenter不断变化和Y方向离轴YDecenter=0mm、X方向离轴XDecenter不断变化时,PSSN的值如图4所示.X方向离轴XDecenter=0mm、Y方向离轴YDecenter=0mm、Z方向倾斜ZTilt=0°时,Y方向倾斜YTilt=0°、X方向倾斜XTilt不断变化与X方向倾斜XTilt=0°、Y方向倾斜YTilt不断变化时,PSSN的值如图5所示.

从上述结果中可以看出,M 3是椭圆形的平面反射镜,沿X方向和Y方向移动,系统的PSSN变化很小,考虑到计算PSSN时点扩散函数取样点个数有限,可以认为PSSN基本不变.M 3分别沿X轴倾斜和Y轴倾斜时,对系统的PSSN有影响.总体来说,随着倾斜角的变大,PSSN变小.

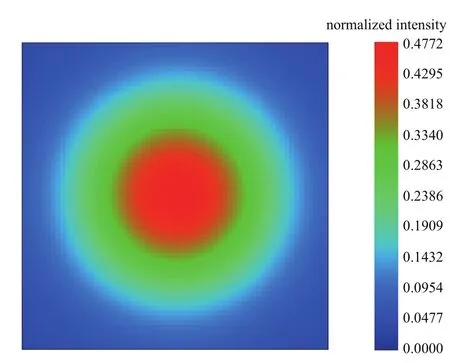
图3 TM T系统的点扩散函数Fig.3 The PSF of TM T system

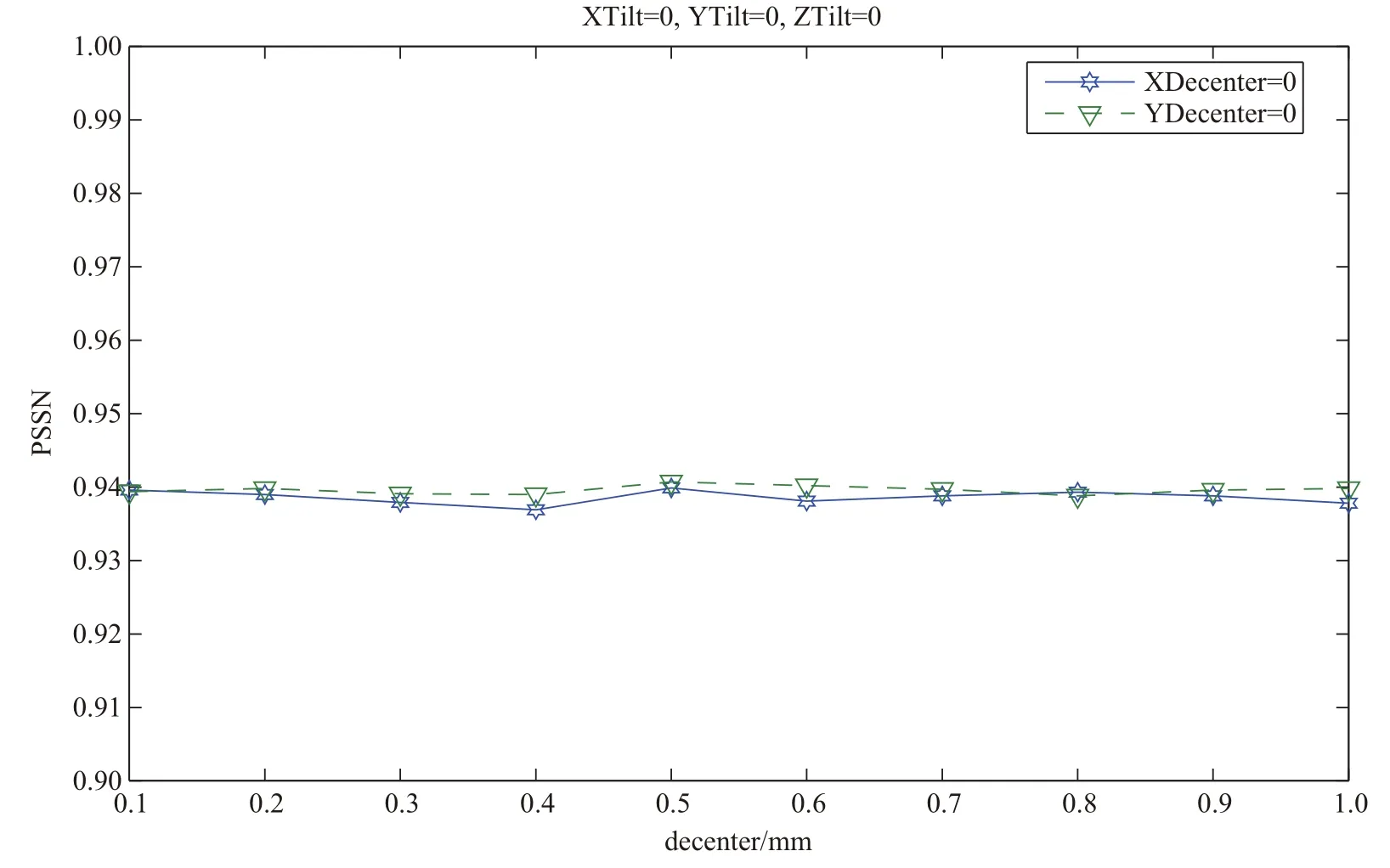
图4 X方向和Y方向分别偏移时系统的PSSNFig.4 The PSSN resp ectively w ith X-and Y-shift

图5 X方向和Y方向分别倾斜时系统的PSSNFig.5 The PSSN resp ectively w ith X-and Y-tilt

3.3.2 准直镜的移动对系统PSSN的影响

对TMT官方提供的文件名为130819v286-red-imaging.zm x的文件,在光瞳面前加入Zernike面,Zernike系数是由3.2节的方法获得.考虑准直镜的偏移对系统PSSN的影响.通过不断移动准直镜,计算系统的PSSN.

当X方向倾斜XTilt=0°、Y方向倾斜YTilt=0°、Z方向倾斜ZTilt=0°时,X方向离轴XDecenter=0mm、Y方向离轴YDecenter不断变化和Y方向离轴YDecenter=0mm、X方向离轴XDecenter不断变化时,PSSN数值如图6所示.X方向离轴XDecenter=0mm、Y方向离轴YDecenter=0mm、Z方向倾斜ZTilt=0°时,Y方向倾斜YTilt=0°、X方向倾斜XTilt不断变化与X方向倾斜XTilt=0°、Y方向倾斜YTilt不断变化时,PSSN的数值如图7所示.

可以看到,随着偏移量和倾斜角的变大,系统的PSSN变小.

3.3.3 系统的PSSN与天顶角的关系

根据Fried参量r0与大气视宁度ε0的关系ε0=0.98λ/r0,可以计算出大气视宁度.在Zemax软件中,通过不断改变天顶角,用3.2节的方法模拟r0=50,100,···,600mm的大气,分别计算系统的PSSN.当W FOS在轴上(OnAxis)时,给定相同的误差,系统的PSSN与天顶角的关系如图8所示.

在大气视宁度不变的情形下,随着天顶角的不断增大,系统的PSSN不断减小.在天顶角不变的情形下,随着Fried参量r0的不断增大,系统的PSSN不断减小.

图6 X方向和Y方向分别偏移时系统的PSSNFig.6 The PSSN resp ectively w ith X-and Y-shift

图7 X方向和Y方向分别倾斜时系统的PSSNFig.7 The PSSN resp ectively w ith X-and Y-tilt

图8 天顶角与系统的PSSN的关系Fig.8 The relation between zen ith angle and PSSN

3.3.4 系统的PSSN与波像差的关系[12]

不断偏移M 3,使系统的波像差较小时,PSSN与波像差的关系近似满足PSSN≈1−αµ2,如图9所示.

当不断较大程度地偏移M 3,使系统的波像差较大时,PSSN与波像差的关系,如图10所示.

可以看到,当波像差较大时,公式PSSN≈1−αµ2不再适用.

4 结论

本文模拟了大气视宁度的简化模型,利用该简化模型,对PSSN在WFOS中的应用进行了研究.结果表明该大气视宁度的简化模型能够应用在考虑大气湍流影响下复杂望远镜系统的像质评价,以及PSSN对视宁度受限下的TMT的像质评价是有效的,验证了在波像差较小的情况下,PSSN与波像差之间的关系.本文首次尝试将近年发展的仅用于望远镜的分析方法扩展到包含宽视场光谱仪器的研究,对仪器及与望远镜的接口开展了相关的应用研究分析.

图9 波像差与系统的PSSN的关系Fig.9 The relation betw een W FE and PSSN o f system

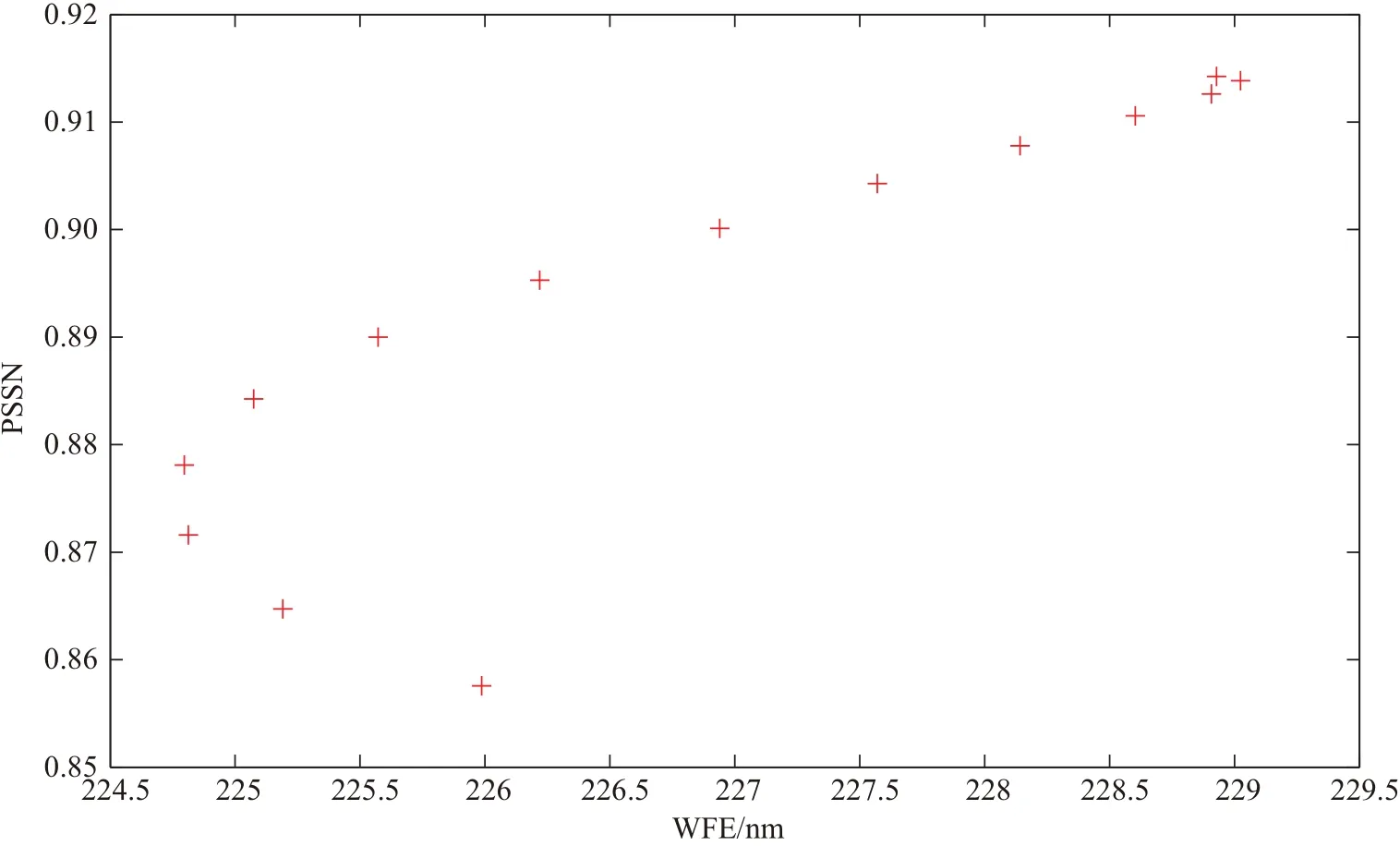
图10 波像差较大时,波像差与PSSN的关系Fig.10 The relation betw een W FE and PSSN w ith a large W FE

参考文献

[1]郁道银,谈恒英.工程光学.第2版.北京:机械工业出版社,2008:193

[2]高波.科技资讯,2008,12:228

[3]Byoung-Joon S,Carl N,George A,et al.ApOp t,2009,48:5997

[4]Goodm an J W,秦克诚.傅里叶光学导论.第3版.北京:电子工业出版社,2011

[5]Byoung-Joon S,Carl N,George A,et a l.SP IE,2008,7017:70170T-1

[6]Rodd ier N A.O p tEn,1990,29:1174

[7]胡朝晖,姜文汉.光电工程,1995,22:50

[8]No ll R J.JOSA,1976,66:207

[9]K onstan tinos V,G eorge Z.SP IE,2008,7017:70170V-1

[10]Byoung-Joon S,Carl N,M itchell T,et a l.A pOp t,2013,52:4111

[11]Doug las G,Carl B,G eorge Z.SP IE,2015,7017:70170W-1

[12]Byoung-Joon S,Carl N,M itchell T,et al.ApOp t,2013,52:3910

The Research on the A pp lication of Norm alized Point Sou rce Sensitiv ity in W ide Field Op tical Spectrom eter of the Th irty M eter Telescope

CHEN Li-si1,2,3HU Zhong-wen1,2

(1 Nationa l A stronom ica l Observatories/N an jing Institute o f A stronom ica l O p tics&Techno logy, Chinese A cadem y o f Scien ces,Nan jing 210042) (2 K ey Laboratory o f A stronom ica l O ptics&Techno logy,Nan jing Institu te o f A stronom ica l O p tics& Techno logy,Chinese A cadem y o f Scien ces,Nan jing 210042) (3 Un iversity of Chinese Academ y o f Scien ces,Beijing 100049)

The image evaluation of optical system is the core of optical design.Based on the analysis and com parison of the PSSN(Normalized Point Source Sensitivity)proposed by the image evaluation of the TMT(Thirty Meter Telescope)and the common image evaluation method,the application of PSSN in the TMT WFOS(W ide Field Optical Spectrometer)is studied.It includes a sim plified simulation of the atmospheric seeing,effects of themovement ofM 3 on PSSN of the system,effects of the collimating m irror movement in the W FOS on PSSN of the system,the relation between PSSN and the zenith angle under the conditions of different atmospheric turbulences,and the relation between PSSN and wavefront aberration.The results show that the PSSN is effective for the evaluation of the TMT under a lim ited atmospheric seeing.

telescopes,image evaluation,methods:numerical

P111;

A

10.15940/j.cnki.0001-5245.2016.05.008

2016-01-07收到原稿,2016-03-05收到修改稿

∗国家自然科学基金项目(11273038)和中国科学院先导B项目(XDB09040104)资助

†lschen@niaot.ac.cn