基于精密光压模型的GRACE卫星加速仪校标新方法∗

汪宏波 熊永清 赵长印

(1中国科学院紫金山天文台 南京 210008) (2中国科学院空间目标与碎片观测重点实验室 南京 210008) (3宇航动力学国家重点实验室 西安 710043)

基于精密光压模型的GRACE卫星加速仪校标新方法∗

汪宏波1,2,3†熊永清1,2赵长印1,2

(1中国科学院紫金山天文台 南京 210008) (2中国科学院空间目标与碎片观测重点实验室 南京 210008) (3宇航动力学国家重点实验室 西安 710043)

以精密光压模型为工具,计算GRACE(G ravity Recovery and C lim ate Experim ent)卫星受到的太阳光压摄动力,以此对加速仪的y轴、z轴的尺度因子进行估算并固定为常值,然后通过动力学定轨方法对另外4项加速仪校标参数(x轴尺度和偏差,y、z轴的偏差)进行求解,得到了2002–2014年每一天的加速仪校标参数.统计结果如下: GRACE-A卫星x、y、z 3个轴的尺度因子分别为0.9435±0.0187、0.9393±0.0444、1.0371±0.0391,GRACE-B卫星3个轴的尺度因子分别为0.9313±0.0170、0.9488± 0.0452、1.0274±0.0446.与早期工作的差异在于,在动力学法定轨之前,先利用精密光压模型对y、z轴的尺度因子进行约束,有助于减小资料误差对弱信号轴(y,z)的影响,从而提高校标结果的稳定性.以GRACE-A卫星的y、z轴为例,尺度因子的标准差约0.0391–0.0444,而未加光压模型约束的动力学校标方法的标准差为0.21–0.31,新方法得到的标准差降幅超过78%;同样,线性偏差的标准差降幅超过85%.因此,新方法得到的校标参数更加稳定,对于研究大气旋转效应以及热层大气风场具有特殊的价值.

天体力学:人造卫星运动,仪器:探测器,地球:大气层

1 引言

GRACE(Gravity Recovery and Climate Experiment)计划是美国国家航空航天局(NASA)与德国宇航中心(DLR)联合实施的重力场卫星探测计划[1].2002年3月两颗GRACE卫星(GRACE-A、GRACE-B)被送入500 km高度、89.5°倾角的极轨近圆轨道.卫星的初始设计寿命为5 yr,至今已经正常工作了14 yr,为地球时变重力场的研究提供了大量的观测资料.为了精确探测引力场,卫星搭载了新型加速仪(Super-STAR),用于测量卫星受到的非引力加速度(太阳光压、大气阻力等).该设备由法国空间技术研究院(ONERA)研制,是CHAMP(CHA llenging M ini-satellite Payload)卫星[2]搭载加速仪的改进版,测量精度达到10−10m/s2.

但是,加速仪的测量值并不是真实的加速度,需要经过一个校标过程,才能得到卫星实际受到的非引力加速度[3−4].国际上通行的校标过程是采用两个参数(尺度因子scalei、线性偏差biasi),加速度aicorrected按照(1)式进行校标:

其中i=1,2,3,分别代表加速仪的3个轴,aiobs为加速度观测值,定义在科学参考系(SF)下,见图1,图中还给出了SF系与轨道坐标系(径向、沿迹和轨道面法向)的关系.

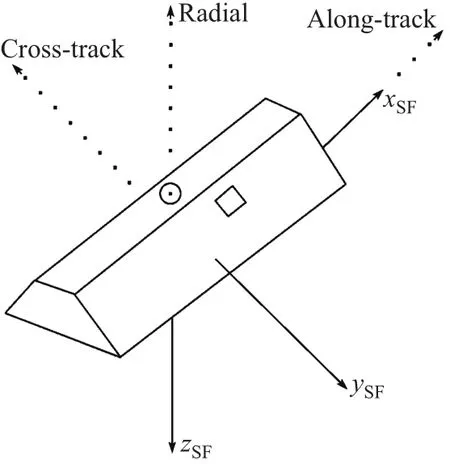
图1 GRACE-A卫星加速仪在SF系中的3轴指向及其与轨道坐标系的关系[5]Fig.1 The defin ition of GRACE-A’s th ree axes in science fram e and its relation w ith orb it coordinate system[5]

针对GRACE卫星的校标,熊永清等人早前提出利用多天资料联合校标的方法,得到了加速仪每天的校标参数[5],其中x轴的结果非常稳定,尺度因子(scale)的标准差为0.02,线性偏差(bias)的标准差为4×10−8m/s2.这主要是因为多天资料联合构建的法方程,采用7 d不变尺度的策略,对阻力信号最强的飞行方向(x轴)进行了很好的约束,保证了结果的稳定性.在x轴资料的基础上,我们反演得到了400–500 km的高层大气密度,并开展了相关研究[6−9].然而,早期结果中y轴和z轴的校标参数却不是很稳定.对于尺度因子, y轴和z轴的结果分别为:0.985±0.31和0.947±0.21,标准差量级较大;对于线性偏差,标准差也达到10−6–10−7m/s2,显著高于x轴偏差的量级(10−8m/s2)[5].本文将针对y轴和z轴,提出一种基于精密光压模型的校标新方法,目标是得到y、z轴更加稳定的校标参数,这对于完整地利用加速仪资料研究高层大气的密度、中性风场、大气旋转等具有重要价值.

2 基于精密光压模型的校标方法

2.1 y、z轴校标存在的困难

2.1.1 y、z轴方向的非引力信号相对较弱

GRACE加速仪的x轴被安置在飞行方向,是3个轴中信号最强的,通常在10−7m/s2量级,大气阻力加速度直接作用在该方向上.而z轴和y轴分别指向天底(顶)和轨道面法向,测量的非引力主要是太阳光压以及大气旋转效应产生的摄动力,数值上比x轴低1–2个量级,信号相对较弱.

2.1.2 轨道在y、z轴方向上变化不显著

对于低轨卫星,较短时间内轨道变化最显著的方向是沿迹方向,即x轴所在的飞行方向.因此,在动力学定轨中x轴的校标参数能较好地确定.而在y、z轴方向轨道变化幅度较小,要从细微的轨道变化中提取加速度信息,存在较大难度.正是由于以上两个特点,使得y、z轴的校标参数在定轨中处于相对次要位置,利用最小二乘求解时,对测量和模型误差特别敏感,从而表现出较大幅度的、不规则的起伏,掩盖了校标参数的固有信息.

为了求解更稳定的y、z轴校标参数,我们认为在轨道信息之外,应该增加一个独立的强约束.具体做法是:在基于动力学方法的统计定轨之前,选择精密光压摄动模型作为独立的强约束条件,把y轴和z轴的尺度因子提前确定下来,降低测量误差对尺度参数的影响;然后在动力学定轨中仅求解这两个轴的偏差参数,使得y、z轴的待估参数从2个降为1个,降低参数间的相关性.而对x轴的校标仍沿用文献[5]的方法,这里不再详述.

2.2 精密光压摄动模型

该方法的前提是精确地计算太阳光压摄动加速度,这不仅要严格计算有效光压面积,还要考虑每个外表面材料的反射系数和散射系数.对于一般的卫星,如果星体信息不清楚,姿态不稳定,是很难准确计算太阳光压的.但是GRACE卫星所受的太阳光压加速度可以精确地计算,这主要得益于以下几个条件:

(1)明确的姿态信息(LEVEL-1B级卫星姿态数据(SCA)文件提供的四元数信息)

(2)准确的轨道信息(LEVEL-1B级快速科学轨道数据(GNV)文件提供的科学轨道,精度达分米级)

(3)精细的星体模型(Macro-Model,包含卫星星体构造、外表面面积、材料反射系数、外表面法向矢量等)

官方详细给出了GRACE-A/B双星的表面材料、外表面法向和面积以及反射系数表.具体可参见文献[10]的I.5.3.5节.在这些信息的基础上,我们选择Box-W ing光压模型精确计算太阳光压.该模型是M ilani等人在1987年提出的太阳光作用在平坦表面的压力加速度计算模型,它是一种精密的光压模型,常用在重力、测高、海洋、导航等卫星的事后数据处理中[11].模型如下:

该模型将卫星本体分成若干个平坦表面,利用每个表面的有效截面积和光压系数计算太阳光压加速度矢量,然后求和得到卫星受到的总加速度.其中,ν是地影因子;ρs是距离太阳表面1 au处(地球附近)的光压强度;m为卫星质量;nface是被光线照射的表面个数,除去了被遮挡的表面;θi是各个表面的法向与光线照射方向的夹角,cosθi=ni·ˆs,ˆs是卫星到太阳的单位矢量,即=rs−r,rs和r分别为太阳和卫星的位置矢量;ni是每个被照射表面的单位法向,注意它和ˆs都应该是在J2000坐标系下;是每个表面的散射系数;是每个表面的镜面反射系数.

通过以上参数和模型,能够计算任意时刻卫星受到的太阳光压加速度.那么,如何利用这个信息计算出y轴和z轴的尺度因子,下面将分别阐述.由于z轴的情况相对简单,先介绍z轴尺度因子的计算方法.

2.3 利用太阳光压摄动在z轴的分量求解z轴的尺度因子

GRACE卫星加速仪的z轴是在轨道面内指向天底或天顶方向(取决于A星或B星).在这个方向,卫星受到的非引力摄动源主要有太阳光压、地球反照等.太阳光压在z轴的加速度分量约1.0×10−8–7.0×10−8m/s2;而地球反照的加速度量级则比较小(约10−10m/s2),接近仪器的极限精度,这里暂不考虑.数值计算还表明:z轴方向还有很小量级的大气旋转加速度分量,通常小于1.0×10−9m/s2,在总加速度中占比小于5%.因此,z轴所记录的加速度几乎绝大部分是由太阳光压所引起的.只要精确计算出太阳光压在这个方向上的加速度分量,就可以对z轴进行校标.

图2是GRACE-A卫星2008年1月3日测量的z轴加速度(图中上半部分)以及理论光压模型计算值(图中下半部分).测量值在5.6×10−7m/s2左右,恒为正值;而理论值在−2×10−8–6×10−8m/s2之间变化,当卫星进入地影后理论值变为0,而实测值也变成了平缓的曲线.实测与理论曲线的形状和趋势完全一致,证明太阳光压在z轴起主导作用,这与前文关于摄动源的分析是一致的.

图2 z轴方向的实测加速度和太阳光压摄动模型理论计算值Fig.2 The acceleration m easu rem ents in z-axis and the theoretical values calcu lated by the solar rad iation pertu rbation m odel

由于两条曲线的相关系数达到0.964,一个直接的想法是将理论曲线与实测曲线拟合,直接得到(1)式中的尺度和偏差.但是更多的数值试验发现,这种方法得到的尺度因子很不稳定,可能是由于加速度曲线是非连续、非闭合的,拟合过程容易受到资料分布的影响,所以不采用直接拟合两条曲线的方法.我们提出,利用卫星每一次进、出地影过程中加速度数值的突变量求解尺度因子.

我们注意到,在图2中的5个轨道周期内卫星9次进出了地影,实测和理论加速度都存在9次突变.通过放大局部曲线可以看到更多的加速度变化细节(图3).在这一天世界时4–6 h之间,卫星经历一次出地影过程(图3中A区域),一次进地影过程(图3中B区域).以A区域为例,卫星先是在地影中,理论光压加速度为0(对应右坐标轴),实测加速度为一条平缓直线(对应左坐标轴);之后卫星出地影,理论值从0突变到−1.726×10−8m/s2,实测加速度也开始从5.491×10−7m/s2下降到5.307×10−7m/s2,降幅1.840×10−8m/s2.若记理论光压加速度的突变量为δmodel,实测加速度的突变量为δobs,那么可以证明尺度因子s为:

证明方法见本节最后部分.

图3 一个轨道周期内的两次地影事件(2008-01-03)Fig.3 The tw o p rocesses o f passing in/ou t earth-shadow du ring one orb it cycle(2008-01-03)

对于区域A发生的出地影事件,可以简单计算出尺度因子sA为:

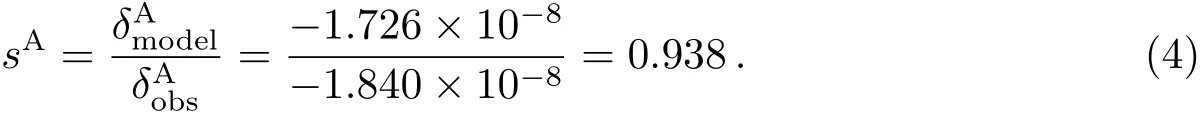
同样,根据区域B发生的进地影事件,可得:

那么尺度因子sB为:

一般而言,每天的资料中大约有29次(最多的情形)进出地影的事件发生,对于每次进出地影事件都能计算一个尺度因子.但是,由于仪器测量值有较多的不规则跳变,在统计δobs时容易受到偶然误差的影响,利用单次地影事件中的δobs直接计算尺度因子会存在不规律的起伏,例如图3中A和B两次地影事件得到的尺度因子就有一定的差别(0.938和0.987).因此需要先对多组地影事件中的突变量δobs和δmodel进行统计平均,然后再求尺度因子.记每次事件的理论突变量和实测突变量分别为和,那么它们的统计平均值分别为:

(7)式求平均值时,先对加速度突变量取绝对值,主要是因为进、出地影时突变量有正负号的差别,如果不取绝对值则会导致求和时正负数相抵消,失去很多有效位数,降低了精度.最后,每一天的平均尺度因子计算公式为:

仍然以2008年1月3日的资料为例,共统计到17次有效进、出地影事件,得到理论和实测突变量的平均值分别为:

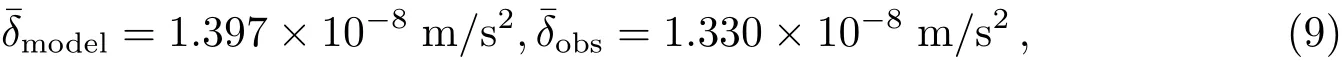
代入(8)式可求出这一天的尺度因子s=1.050.

至此,我们建立了z轴尺度因子的计算方法,通过处理2002年4月至2014年12月的资料,可以得到每一天的z轴尺度因子,见图5.绝大部分尺度因子在0.9–1.1之间变化,总体的平均值为1.0371,标准差为0.0391.为了与文献[5]的结果(前300 d统计,z=0.947±0.210)对比,我们也计算了前300 d尺度因子的平均值和标准差为z= 1.0447±0.0417,可以看出本文方法的标准差显著降低了80%,证明该方法得到的尺度因子更加稳定.

为了分析z轴尺度的长期变化,我们统计了尺度因子的年平均值和标准差,见图6.尺度因子最大值为1.0544(2003年),最小值为1.0048(2014年);标准差最大值为0.051(2012年),最小值为0.029(2010年).总体上看尺度因子呈长期下降趋势.

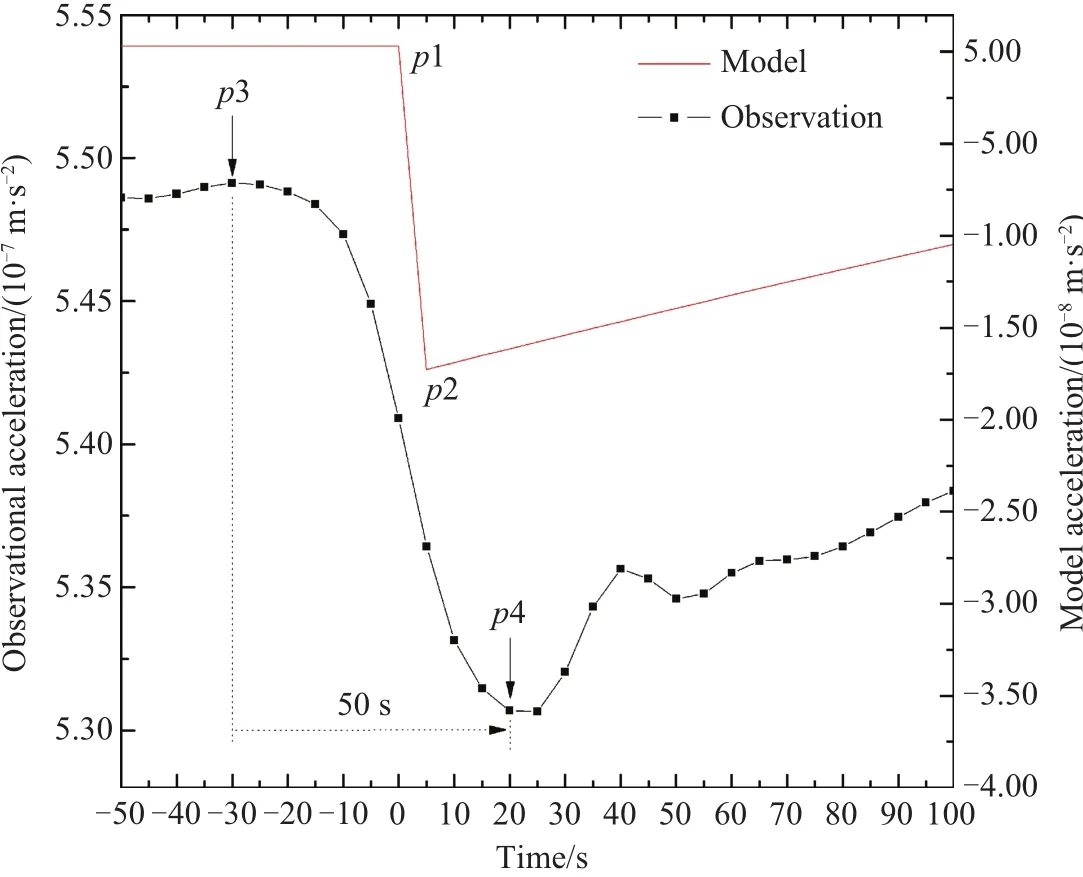
图4 图3区域A所示的出地影事件中加速度曲线图Fig.4 The acceleration cu rves w hen passing ou t earth-shadow show n in region A o f Fig.3

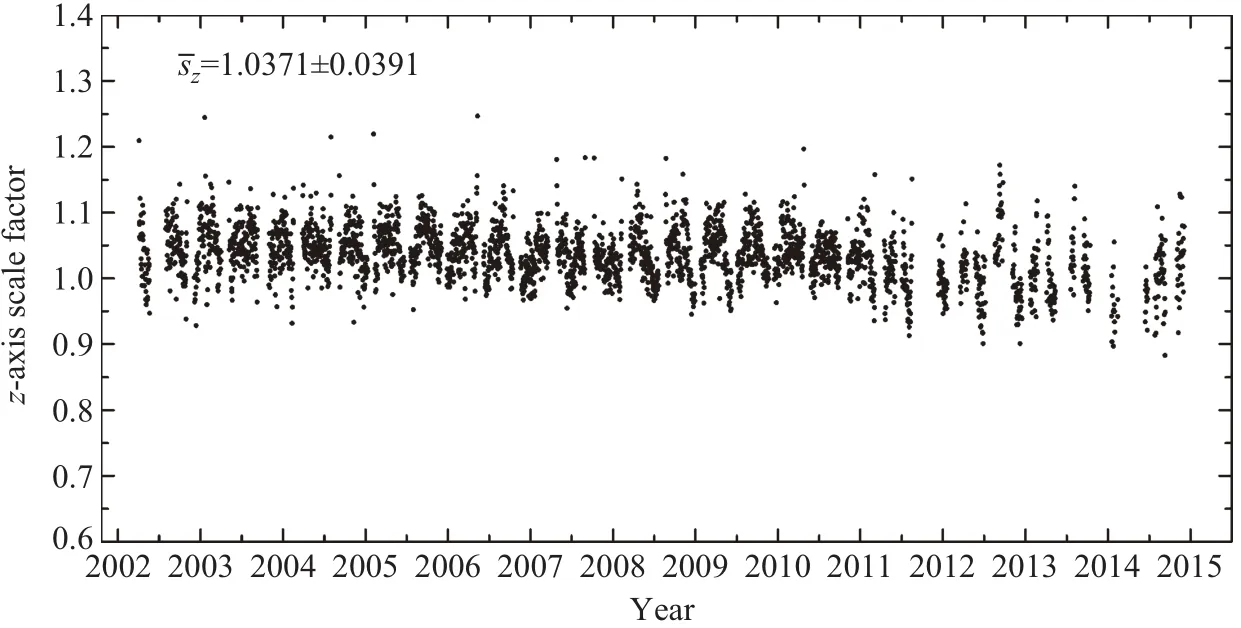
图5 GRACE-A卫星z轴的尺度因子Fig.5 The sca le factors o f z-ax is of GRACE-A

下面给出尺度因子计算(3)式的证明.从校标(1)式出发,略去3个轴的标记i,记校标前的加速度测量值为aobs,校标后的加速度为areal,意味着校标后加速度为实际加速度.以卫星从地影区进入非地影区的事件为例,在地影区内有:

出了地影区之后有:

对于一次出地影的加速度突变事件,把(10)式和(11)式相减,消去方程右边的偏差bias后整理得到:

加速度突变事件发生前,卫星在地影内不受太阳光压(用0表示),卫星只受量级很小的大气阻力(大气旋转引起),即:

卫星出了地影区后,除了大气阻力之外,还会受到太阳光压,那么有:

将(13)式和(14)式相减,得到

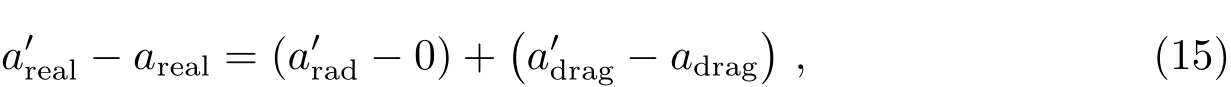
(15)式右边第1部分为光压加速度从无到有所产生的突变,可用理论光压模型计算得到,也就是图2中的光压模型曲线的突变量δmodel;(15)式右边第2部分为出地影前后大气阻力加速度的差异,由于它在短时间(1–2m in内)的变化量仅为10−10m/s2,相对于光压加速度突变量δmodel的10−8–10−7m/s2量级而言,这种变化量是可以忽略的,即认为:

所以(15)式改写为

再代入(12)式,有

证明完毕.

2.4 利用太阳光压摄动在y轴的分量求解y轴的尺度因子

加速仪的y轴是轨道面外法向(与轨道面垂直),在这个方向上,主要的非引力摄动源是大气旋转引起的加速度分量和太阳光压.我们仍然以2008年1月3日的数据为例(图7).图的上半部分是加速仪y轴的实测值,而下半部分是理论光压模型计算得到的加速度.对比发现,实测值与理论值的曲线走势基本一致,说明光压加速度仍然在y轴加速度中占较大比重,主导了曲线的走势.

图7 y轴方向的加速度测量值和太阳光压摄动模型理论计算值Fig.7 The acceleration m easu rem en ts in y-axis and the theoretical va lues ca lcu lated by the so lar rad iation pertu rbation m odel

当卫星进、出地影时y轴加速度实测和光压理论值都有显著的突变.图7中标记了3次加速度突变现象(区域A、B、C),这一特征与之前z轴的情形相似.不同之处在于, y轴的实测加速度中还有一定程度的大气阻力加速度(大气旋转引起),但可以肯定A、B、C区域的加速度突变是由太阳光压单独造成的,因为大气阻力加速度是连续变化的,不会出现突变.

在利用y轴加速度突变量计算尺度因子时,基本原理与z轴的处理方法一致,但是需要额外考虑大气旋转所引起的阻力加速度对突变量δobs的影响.因为在y轴方向,这种加速度与光压基本在同一个量级上(10−8m/s2),突变前后阻力加速度的差异不再是可以忽略的小量,即(16)式不再成立,所以(15)式等号右边第2部分不能忽略,需要完整计算,这里采用通用的大气旋转计算公式[12]计算大气旋转阻力加速度在y轴的分量.

图8是对2002–2014年GRACE-A卫星的y轴校标结果,大部分尺度因子在0.8–1.2之间变化,平均值为0.9393,标准差为0.0444,总体上存在递减的趋势.为了与早期结果对比,我们还统计了GRACE-A卫星前300 d资料的校标结果,显示平均值为0.981,标准差为0.072.对于相同时期的资料,文献[5]的结果是0.985,标准差为0.310.由此可见,本文结果的标准差比早期结果显著减小(降幅约77%),尺度因子更加稳定.

图8 GRACE-A卫星y轴尺度因子Fig.8 The sca le factors o f y-ax is o f GRACE-A

为了分析尺度因子的长期变化,我们统计了2002–2014年的年平均值和标准差,结果见图9.GRACE-A的y轴尺度因子最大值0.9738,最小值0.9149,标准差最大值0.076 (2014年),最小值0.021(2006年).总的来看,尺度因子整体呈现下降趋势,标准差在太阳活动谷年较小,在太阳活动峰年较大.

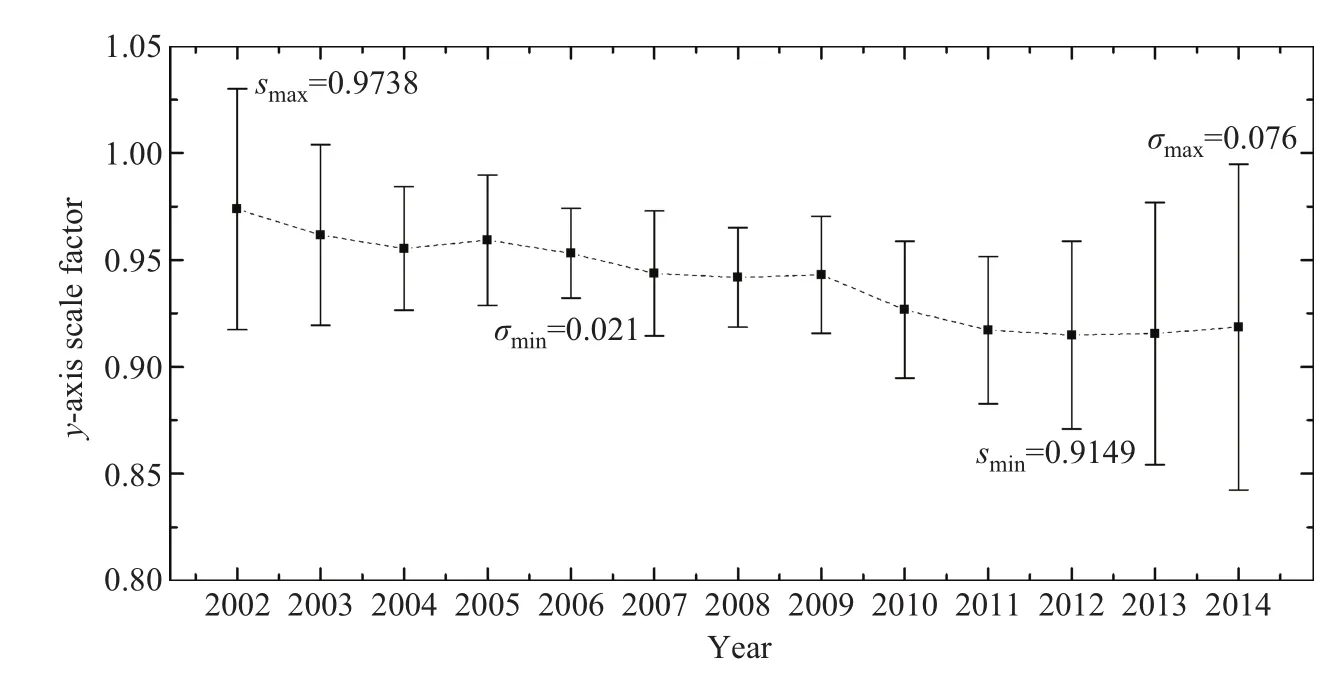
图9 GRACE-A卫星y轴尺度因子的年平均值和标准差Fig.9 The sca le factors’yearly averages and standard deviations o f y-ax is o f GRACE-A

至此,我们已经完整地给出了用卫星进、出地影前后加速度的突变现象估计y、z轴的尺度因子的方法,并解算了2002年4月至2014年12月的尺度因子序列.在动力学定轨环节,将尺度因子固定下来,仅求解两个轴的线性偏差参数.

需要补充说明:当卫星轨道面与太阳位置呈特定关系时(一般在轨道面处于晨昏线附近),卫星在整个轨道周期内都处在地影区之外,不进入地影,也就不产生加速度突变现象,那么这种方法就失效了.对于这种情况,则采用前一天的尺度因子作为先验值代替,或者用这一天所在年份的平均值代替.尽管y、z轴尺度采用先验值近似,但在定轨中还是会重新估计这两个轴的线性偏差,因此即使尺度因子存在一定误差,在动力学校标阶段也可以被线性偏差参数所吸收,使得利用(1)式修正后的总加速度值不会有误差.

2.5 定轨资料与动力学模型

采用的数据是德国地球科学研究中心GFZ(Helmholtz-Centre Potsdam-German Research Centre for Geosciences)发布的GRACE卫星LEVEL-1B GNV,作为轨道的“伪观测量”,并辅以姿态数据和加速仪数据(ACC),取代大气阻力经验模型和光压模型.动力学法精密定轨采用的模型和基本参数见表1.

表1 动力学定轨所采用的摄动模型和基本参数Tab le 1 M odels an d p aram eters used in the d ynam ica l orb it determ ination

3 校标结果与合理性检验

3.1 校标结果的统计平均(2002–2014)

通过处理GRACE-A/B双星2002–2014年的资料,得到了每颗卫星3个坐标轴的6个校标参数序列,表2是各参数的统计平均值和标准差.以GRACE-A的y轴和z轴为例,尺度因子约为0.9393和1.0371,线性偏差在10−5–10−7m/s2的量级.两颗星的结果比较相似,因为它们搭载的是完全相同的仪器.

相对于早期结果(取自文献[5]的表1),本文方法得到的参数标准差显著降低,意味着校标参数的稳定性得到显著提升.从GRACE-A卫星y轴和z轴统计结果看,尺度因子的标准差从早期的0.21–0.31降低到0.045左右,降幅超过78%;对于线性偏差,y轴的标准差从原来的8.57×10−6m/s2下降到4.68×10−7m/s2,z轴从1.49×10−7m/s2下降到2.12×10−8m/s2,降幅超过85%.

3.2 与不加外部约束的动力学法对比(2002–2008)

本节把不加外部约束的动力学定轨方法(文献[5])和本文方法进行对比,同时给出官方在2009年发布的推荐值[3],它是在一组线性公式中输入简约儒略日计算得到,一般用作迭代过程的初始值.

图10是x轴的对比,图的上半部分是尺度因子,图的下半部分是线性偏差,未加精密光压约束的方法结果标记为灰色点,本文方法标记为黑色点实线,官方推荐值是直线.图中POD为精密定轨,从尺度因子的结果可以看出灰色点比较离散,表明未加约束的方法得到的参数有较大的起伏,而本文方法相对稳定一些,线性偏差的图也有这种特征.这说明,即使没有对x轴做额外约束,精密光压模型对y、z轴尺度因子的约束作用也能一定程度上减弱x轴参数的不规则起伏.

表2 GRACE-A/B双星校标参数的统计Tab le 2 The statistic o f GRACE-A/B tw in satellites’calib ration param eters

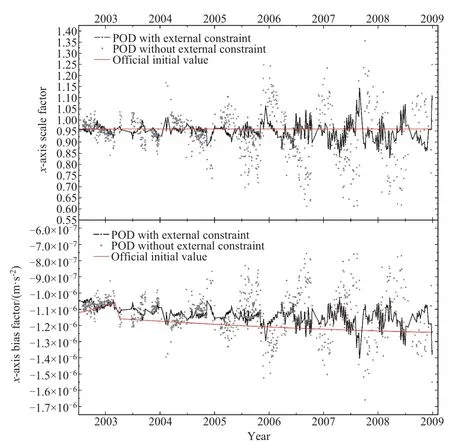
图10 不同校标方法估计的x轴尺度因子及线性偏差和官方推荐值对比(GRACE-A)Fig.10 The com parison am ong the sca le and b ias factors o f x-axis estim ated by d ifferent m ethods and officia l recomm endation va lue(GRACE-A)

图11和图12分别是y轴和z轴的对比,都显示本文方法得到参数更加稳定,整体趋势与官方推荐值在长期趋势上保持一致.

图11 不同校标方法估计的y轴尺度因子及线性偏差和官方推荐值对比(GRACE-A)Fig.11 The com parison am ong the scale and bias factors o f y-ax is estim ated by d ifferen t m ethods and officia l recomm endation va lue(GRACE-A)

3.3 校标结果的合理性检验

为了检验校标结果是否合理,根据常用的做法[4−5],我们分析了动力学定轨残差以及两颗星校标后在飞行方向的加速度差值.

(1)动力学定轨后的资料残差

如果校标参数是合理的,那么动力学定轨后资料残差应当尽量小,表明定轨过程是收敛的,校标参数在最大程度上还原了非引力加速度.根据2002–2014年的定轨结果, GRACE-A星的资料残差平均值为24.3 cm,GRACE-B星的残差平均值为24.1 cm,已经非常接近定轨所用GNV数据的精度水平(20 cm),可见收敛效果是非常好的,校标结果是合理可信的.

(2)A星和B星在飞行方向(x轴)加速度差值

由于两颗星是共轨的,前后相距约220 km,到达同一空间位置的时间差约30 s,这么短的时间内可以近似认为大气密度没有显著变化,所以两颗卫星在飞行方向(x轴)同一空间位置上所受到的大气阻力应该是近似相等的.根据这一个特点,在任一时刻以A星为基准,把B星的加速度插值到A星所在的空间位置,得到同一位置下B星的x轴加速度,然后与A星相比较,得到两个加速度的差值.图13是2008年1月3日A星和B星加速度曲线对比(匹配插值后,前6 h的局部放大),可见两条加速度曲线完全重合,绝对差异在这一天内的平均值为3.7×10−10m/s2,这个量级已经与加速仪的测量精度非常接近,可以忽略不计,把两者看作近似相等.当然,这仅仅是一天的个例,我们还统计了2002—2014年两颗卫星的全部资料,得到飞行方向的加速度差值的统计平均值为2.3×10−10m/s2,证明两颗星独立校标后,在飞行方向的加速度完全吻合,校标结果得到了相互印证.

图12 不同校标方法估计的z轴尺度因子及线性偏差和官方推荐值对比(GRACE-A)Fig.12 The com parison am ong the sca le and b ias factors o f z-axis estim ated by d ifferen t m ethods and officia l recomm endation va lue(GRACE-A)

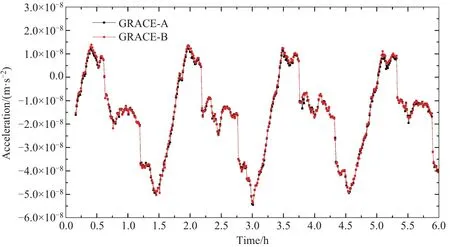
图13 校标后两颗卫星在飞行方向加速度的比较Fig.13 The com parison betw een the corrected accelerations o f GRACE-A and GRACE-B in a long-track d irection

4 结论

本文以精密光压摄动模型为工具,对GRACE卫星加速仪的y轴、z轴的尺度因子进行了约束,然后通过动力学定轨方法对2002—2014年每一天的加速仪校标参数(x轴的尺度和偏差,y,z轴的偏差)进行了求解.统计结果如下:GRACE-A卫星x、y、z等3个轴的尺度因子分别为0.9435±0.0187、0.9393±0.0444、1.0371±0.0391,GRACE-B卫星3个轴的尺度因子分别为0.9313±0.0170、0.9488±0.0452、1.0274±0.0446.相对于早期的结果,y轴和z轴尺度因子的标准差降幅超过78%,线性偏差的标准差降幅超过85%.因此,本文方法更加稳定地标定了加速仪3个轴,特别是对信号强度较弱的y、z轴改进明显,这对于科学、完整地分析和使用GRACE卫星的星载加速仪资料具有促进作用.

[1]Tap ley B D,Bettadpu r S,W atkins M M,et al.GeoRL,2004,31:L09607

[2]Reigber C,L¨uh r H,Schw in tzer P.A d SpR,2002,30:129

[3]Srin ivas B.Recomm endation for A-p riori B ias&Sca le Param eters for Level-1B ACC Data(Version 2),GRACE TN-02,2009

[4]熊永清,汪宏波,赵长印.天文学进展,2011,29:228

[5]熊永清,汪宏波,许晓丽.中国科学:物理学力学天文学,2011,41:1319

[6]汪宏波.天文学报,2010,51:435

[7]汪宏波,赵长印.天文学报,2008,49:168

[8]W ang H B,Zhao C Y.ChA&A,2008,32:388

[9]W ang H B,Zhao C Y.ScChG,2009,52:7

[10]Srin ivas B.G ravity Recovery and C lim ate Exp erim en t P roduct Sp ecification Docum en t,GRACE 327-720(CSR-GR-03-02),2006

[11]M ilani A,Nobili A M,Farinella P.Non-gravitational Pertu rbations and Satellite G eodesy.B risto l: A dam H ilger,1987

[12]Liu L.O rb it Theory of Spacecra ft.Beijing:Nationa l Defense Industry P ress,2000

The N ew Calib ration M ethod of A ccelerom eter in GRACE Satellites Based on P recise Solar Rad iation M odel

WANG Hong-bo1,2,3XIONG Yong-qing1,2ZHAO Chang-yin1,2

(1 Pu rp le M oun tain O bserva to ry,Chinese A cadem y o f Scien ces,Nan jing 210008)
(2 K ey Laboratory o f Space Object and Debris Observation,Pu rp le M oun tain Observatory,Chinese A cadem y o f Scien ces,Nan jing 210008) (3 State K ey Laboratory o f A stronau tic D ynam ics,X i’an 710043)

In this paper,we adopt the precise solar radiation model to com pute the realperturbation force caused by solar radiation on the GRACE satellites,and estimate the scale factorsofaccelerometer’s y-axisand z-axis,which are set to be constant values in the follow ing calibration process.Then,we estimate the rest of four parameters by the dynam ic orbit determ ination(OD),such as the scale factor of x-axis,and the biases of three axes.Through these steps,we get the daily calibration parameters from 2002 to 2014.The average value and standard deviation of scale factors of x-,y-, and z-axis are 0.9435±0.0187,0.9393±0.0444,1.0371±0.0391 for GRACE-A,and 0.9313±0.0170,0.9488±0.0452,1.0274±0.0446 for GRACE-B,respectively.Different from our early work,the new method constrains the scale factors of y-axis and z-axis w ith the precise solar radiation model,which could decrease themeasurement error’s effect on the weak-signal axes(y,z)as well as reduce the correlation between scale factor and bias,and eventually improve the stability of calibration parameters.Taking the results of y-and z-axis of GRACE-A as examp le,the standard deviation of scale factors w ith the new method is about 0.0391–0.0444,while the early results by the unconstrained dynam ic orbit determ ination are about 0.21–0.31.It is shown that the standard deviations of scale factor w ith this paper’smethod have been decreased by more than 78%,and those of bias have been decreased by more than 85%.Therefore, the calibration parameters estimated w ith the new method aremore stable than our early results,and w ill have a special value for the study on the rotation speed and w ind field of the earth’s thermosphere.

celestialmechanics:themotion ofman-made satellite,instrumentation: detectors,earth:atmosphere

P138;

A

10.15940/j.cnki.0001-5245.2016.05.005

2016-03-03收到原稿

∗宇航动力学国家重点实验室开放基金资助

†whb@pmo.ac.cn