基于天体测量法探测系外行星的仿真模拟与轨道求解算法∗

黄平辉 季江徽

(1中国科学院紫金山天文台 南京 210008) (2中国科学院行星科学重点实验室 南京 210008) (3中国科学院大学 北京 100049)

基于天体测量法探测系外行星的仿真模拟与轨道求解算法∗

黄平辉1,2,3†季江徽1,2‡

(1中国科学院紫金山天文台 南京 210008) (2中国科学院行星科学重点实验室 南京 210008) (3中国科学院大学 北京 100049)

天体测量法是探测系外行星一种有效的手段,具有其他探测方法所不具备的独特优势,如可以探测到行星的3维轨道参数及确定行星的质量等,这些将为现有的行星样本提供重要补充.高精度的空间天体测量卫星Gaia(G lobal Astrometric Interferometer for Astrophysics)在2013年成功发射升空,可以预期未来基于其探测数据,将可能发现大量的长周期类木行星.针对αCentauri A、HD 62509和GJ 876系统,根据Gaia单次天体测量精度生成对应的仿真数据,使用Lomb-Scargle周期谱分析行星轨道周期信号,并采用M arkov Chain Monte Carlo(MCMC)算法对行星系统进行轨道反演,得到的结果与行星的初始参数相吻合.

天体测量学,行星与卫星:演化,天体测量卫星:Hipparcos,Gaia,方法:Lomb-Scargle周期谱,MCMC

1 引言

1995年,Mayor等人通过地面视向速度观测发现第1颗围绕主序星公转的系外行星——飞马座51 b[1],迄今已有3000多颗系外行星通过不同的方法被发现(见图1).目前探测系外行星主要有以下方法:视向速度法(Radial Velocity),凌星法(Transit), TTV(Transit Tim ing Variation)法,直接成像法(Direct Imaging),微引力透镜法(M icrolensing),脉冲星计时法(Pulsar Tim ing)和天体测量法(Astrometry).由图1可知,目前发现大多数系外行星通过视向速度法和凌星法被发现.在早期,系外行星主要通过地面上的视向速度观测发现,而在2009年美国航空航天局(NASA)发射的Kelper卫星通过凌星法发现了4600多颗有凌星信号的系外行星候选体,其中大部分据信是行星.2010年,M uterspaugh等人基于天体测量法利用Palomar天文台的PHASE(Palomar High-precision Astrometric Search for Exoplanet System s)巡天计划发现了一颗疑似质量为1.5MJupiter的行星HD 176051 b[2].2013年,欧空局(ESA)成功发射了新一代高精度天体测量卫星Gaia,这将会极大推动系外行星的发现,进而揭示行星系统的多样性与复杂性.

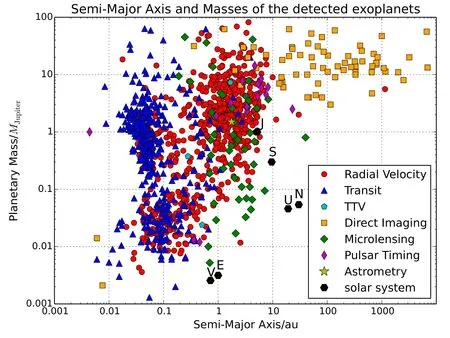
图1 已被发现的系外行星的半长径与行星质量.横坐标为行星的轨道半长径,纵坐标为行星质量,太阳系内的行星由黑色六边形表示,数据来源于exop lanet.eu.Fig.1 The sem i-m a jor axes and m asses of the detected exop lanets.The x-coord inate ind icates the sem i-m a jor ax is o f p lanets,and the y-coord inate ind icates the p lanetary m ass.The p lanets of so lar system are show n as b lack hexagons.The data cam e from exop lanet.eu.

与视向速度法和凌星法比较,天体测量法有如下特点:(1)可以给出行星的轨道倾角i,解除行星质量与轨道倾角的简并,从而导出行星的质量,结合视向速度观测可求解出行星的全部动力学参数,从而建立行星的3维轨道[3];(2)视向速度法和凌星法更容易发现偏心率大的行星系统,而天体测量法则容易观测到偏心率小的行星系统[4];(3)视向速度法和凌星法易于探测短周期和edge on(倾角i=90°)的行星系统,而天体测量法则易于探测到长周期和face on(倾角i=0°)的行星系统,可丰富目前的行星样本;(4)视向速度法要求观测恒星是中晚型、低自转速度、色球活动性弱的恒星[2],而天体测量法对恒星类型、恒星自转速度要求较低、受恒星表面黑子、耀斑、非径向对流的影响较视向速度法要小,由此更容易探测围绕小质量恒星公转的行星[5];(5)天体测量法广泛应用于双星观测,因此易于从双星观测中发现系外行星[2].

天体测量学是古老的天文学分支,是关于位置的天文学,通过测量目标天体在天球上的位移与速度,给出天体的坐标、自行和视差等信息.地面上的天体测量历史悠久,最早完善的星表可追溯到第谷(Tycho)时期.1989年,欧空局发射了Hipparcos(High precision parallax collecting satellite),首次在太空中以高精度的天体测量对太阳附近的恒星进行观测,并给出了高精度的Hipparcos星表[6].作为Hipparcos的继任者,经过数据优化处理后,Gaia将有能力最终以最优至10µas的精度进行天体测量观测[7]. Gaia的核心科学目标是测量银河系约10亿颗恒星(银河系恒星数的百分之一)的自行、视差、视向速度和相关的恒星参数,建立3维的银河系模型,同时Gaia有能力在5 yr的工作寿命内探测约20000颗的长周期类木行星[7].而国内正积极推进的天体测量空间卫星STEP(Search for Terrestrial Extra-solar Planet),期望以最优至1µas的窄角天体测量精度来探测发现距离太阳15 pc内的类地行星.

本文第2节介绍天体测量法探测系外行星的原理；第3节介绍寻找周期信号及进行轨道拟合中所采用的方法；第4节将针对3个具体的算例(αCentauri A、HD 62509和GJ 876),开展行星轨道参数反演研究；第5节将对天体测量法探测系外行星中的问题进行讨论；第6节为总结与展望.

2 天体测量法探测系外行星

2.1 天体测量法探测系外行星原理

天体测量可给出恒星的5个天体测量参量:赤经(α),赤纬(δ),赤经自行(µ∗α),赤纬自行(µδ)和周年视差(ϖ).当恒星存在行星围绕其公转,行星会对恒星造成额外的一个小幅度的周期性椭圆摆动.因此可通过测量恒星在天球上的位置变化来探测系外行星,在恒星的运动中减去恒星自行与周年视差,然后通过对残差进行细致的傅立叶分析后,确认最强的周期信号为行星引力扰动造成,最后再对行星进行轨道拟合.

行星对恒星造成的天体测量信号α(Astrom etric Signature)[8]:

a为行星的轨道半长径,d为恒星离太阳的距离,M∗为恒星的质量,Mp为行星的质量.木星质量行星在1 pc距离、5 au处围绕太阳质量恒星公转造成的天体测量信号为5mas;地球质量行星在1 pc距离、1 au处围绕太阳质量恒星公转造成的天体测量信号为3µas.

由图2可知,目前探测到的大多数系外行星的天体测量信号都小于1mas,而通过凌星法发现的系外行星的天体测量信号大部分小于1µas[7].洋红色框表示Gaia在5 yr的工作期限内可以观测到轨道周期大于0.2 yr小于6 yr、天体测量信号大于10µas的行星[7]；靛蓝色框表示STEP预计能观测到轨道周期大于0.2 yr小于5 yr、天体测量信号大于1 µas的行星.

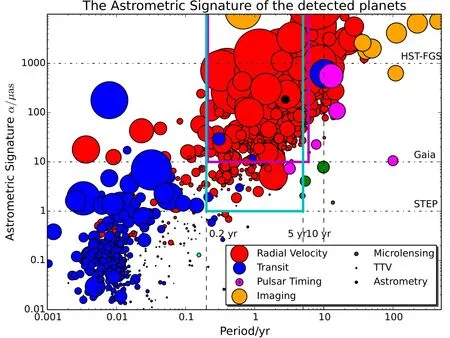
图2 已探测到的系外行星的天体测量信号,横坐标为行星的轨道周期,纵坐标为行星的天体测量信号,点的大小正比于行星的质量[7].HST-FGS(F ine G u idance Sensor)、G aia和STEP的探测精度用点虚线标注.Fig.2 The astrom etric signatu re o f detected exop lanets.The x-coord inate ind icates the period o f p lanets,and the y-coord inate ind icates the astrom etric signatu re.The size o f p oints is p rop ortiona l to the p lanetary m ass[7].The detective ab ilities of HST-FGS(Fine Gu idance Sensor),Gaia,and STEP are p resented by the dot-dashed lines.

系外行星围绕恒星运动的轨道参数定义见图3：轨道半长径a,偏心率e,轨道倾角i,升交点经度Ω,近星点角距ω和过近星点时刻τ.选取天球切平面作为系外行星轨道的参考平面,天球切平面与轨道平面的夹角定义为轨道倾角i(0°–90°),升交点经度Ω为两平面交线北点的位置角,过近星点时刻τ由真近点角ν(t)表示[8].

图3 系外行星轨道参数的定义[8]Fig.3 The definition o f orbita l elem en ts o f an exop lanet[8]

将图3轨道根数(a,e,i,Ω,ω,τ)和轨道周期P、行星质量mp转化为Thiele-Innes根数[9]:

在(2)式中A、B、F、G为Thiele-Innes根数,E(t)为行星的偏近点角.

对于存在n颗行星的系统,如果行星之间的相互引力作用在观测时间内可以忽略(线性化),则恒星在天球切平面上赤经、赤纬方向的变化分别为

Πα,t和Πδ,t分别为赤经、赤纬方向上的视差因子,˙µ∗α和˙µδ为恒星自行的加速项.对于绝大多数恒星,在短时间的观测时间段内,自行的加速项是可以忽略的.因此采取上述的线性化模型,共需要求解7n+5个参数,含5个天体测量参数(α,δ,µ∗α,µδ,ϖ)和n颗行星各7个参数(P,e,i,Ω,ω,τ,mp).

2.2 天体测量法与视向速度法结合

对于已由视向速度法发现的系外行星系统,可通过下式来联合视向速度数据和天体测量数据进行同时拟合[2]:

其中K为行星运动对恒星引起的视向速度半幅度(Radial Velocity Sem i-Amp litude),定义如下[10]:

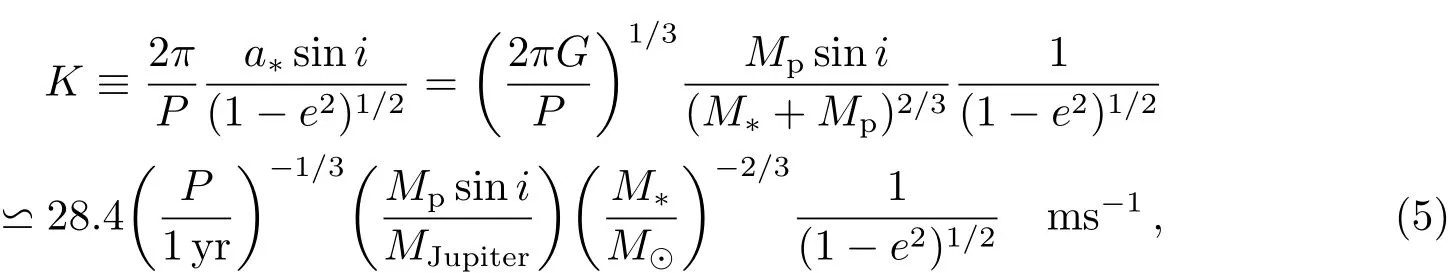
例如木星以周期为11.86 yr围绕太阳公转,对太阳造成的视向速度半幅度为12.5ms−1.

3 算法

3.1 Lom b-Scarg le周期谱

视向速度数据和天体测量数据是时序信号数据,对于非均匀采样的时序信号,可以使用改进的快速傅立叶变换算法Lomb-Scargle周期谱,找出周期信号[11−12]

tj为时间,Xj为时序信号,PX(ω)为Lomb-Scargle周期谱功率,τ由下式计算所得:

值得注意的是,Lomb-Scargle周期谱与使用正弦函数作最小二乘拟合得到的结果并无差别,同时PX(ω)并不代表真实的正弦信号拟合幅度,而是代表信号的统计显著性[12].

由于恒星自转周期、恒星活动性周期、行星间相互摄动、观测采样方案的周期性及行星轨道的偏心率,甚至随机噪声也会引起周期谱中异常的信号峰(alias),需要对周期谱中的alias进行辨认.Lomb-Scargle周期谱的FAP(False A larm Probability)功率值z0可由下式计算[12]:

p0为出现假信号的可能性,即FAP,N为选取的频率计算数目.

3.2 M arkov Chain M on te Car lo(M CM C)

从观测数据中确认行星周期信号后,需要对行星进行轨道拟合,一般使用LM (Levenberg-Marquardt)算法[13]或MCMC(Markov Chain M onte Carlo)算法[14−17]进行轨道拟合,求出行星的轨道参数.LM算法特点是计算速度快,但容易得到局部最优解,而MCMC算法能得到全局最优解,但耗费时间长,而本文的所举算例均使用MCMC算法进行轨道拟合.MCMC算法的原理可简单表示为

其中

χ为归一化的行星过近星点时刻,M1表示恒星周围存在行星,p(M1|I)为M1的先验概率分布,p(D|M1,I)为M1的似然函数,p(D|I)为全局似然函数.p(P,α,e,i,Ω,ω,χ|M1,I)为求解参数的先验概率之乘积,积分的上下限由所求解的参数范围确定.对于信噪比高的情况,可以使用均匀分布作为求解参数的先验分布.而对于信噪比低的情况,则使用Jeffrey分布作为求解参数的先验分布[15].

4 算例

为了说明拟合方法,本文中我们选取3个算例:αCentauri A、HD 62509和GJ 876.αCentauri A目前并没有发现有系外行星围绕,HD 62509则伴有1颗木星大小的行星,GJ 876则发现存在4颗行星.由文献[7]的表2可知Gaia在未来的5 yr任务中有可能分别对它们进行107次、52次和52次的观测(其单次观测精度为34.2µas).对于Hipparcos和Gaia这类广角巡天天体测量卫星,对某一天区的观测依赖于卫星本身的姿态与轨道[18].在Gaia正式释放数据之前,其轨道与姿态及对某一天区的观测方案是不可知的,因此模拟数据中暂不考虑这些因素所带来的影响,而观测时刻是均匀分布随机生成的.对于窄角天体测量观测,通常需要有背景星定标,但在本文中我们不考虑这些数据的预处理过程,同时本文作为行星轨道拟合的示例,采用的恒星的视差与自行数据在拟合过程中视为恒值,不参与拟合,也不考虑星表本身所带来的误差.因此对于n颗行星的系统,这里只拟合7n个参数.

4.1 αCen tau ri A

αCentauri是距离太阳最近的双星,距离仅为1.34 pc,同时αCentauri还与比邻星(Proxima Centauri)组成三合星系统.2012年Dumusque等人通过视向速度发现αCentauri B存在一颗地球大小、周期为3.2357 d的行星[19],但在2016年Ra jpau l等人却证实α Centauri B b是不存在的,之前的行星信号是由于视向速度观测的窗函数所造成[20],因此在这里我们不选取αCentauri B b作为例子.

αCentauri A的光谱型与太阳均为G2V型[21],质量为1.1 M⊙[22],我们模拟产生了一颗海王星质量的行星b在3 au处的椭圆轨道围绕αCentauri A公转(其他轨道根数预先假定或随机产生),加入Gaia单次天体测量观测的精度34.2µas的正态分布误差[7],生成107组天体测量的模拟数据.因为αCentauri双星的半长径为35.6 au,轨道周期为79.91 yr[19],对于5 yr的观测来说影响较小,因此模拟数据中没有考虑另一颗恒星引力作用对模拟数据的影响.

由模拟数据得到图4的Lomb-Scargle周期谱,可以看到存在一个周期约为1750 d的周期信号,信号的FAP低于0.01%,因此可以认为是真实的周期信号,而并非由于随机噪声引起.我们对这个信号进行MCMC模拟,得到表1中模拟行星b的拟合结果及拟合误差.值得注意的是,行星b的周期真值约1810 d,拟合值约1769 d,与Lomb-Scargle周期谱给出的值略有不同,这是由于Lomb-Scargle周期谱的低频率部分的分辨率不足和信噪比不高所造成.单独的天体测量观测存在简并性,升交点经度和近星点角距各有±180°的不确定性,因此表1给出的是近星点经度(longitude of pericentre,ϖ=Ω+ω).同时拟合的是开普勒运动椭圆,过近星点时刻可由过特定时刻的平近点角M0表示,采取的时刻是JD 2457023.5,即2015年1月1日0时0分(UTC),图5为归一化天体测量拟合曲线及拟合残差.

表1 αCentauri A b的拟合参数Tab le 1 The fitting p aram eters o fαCen tau ri A b

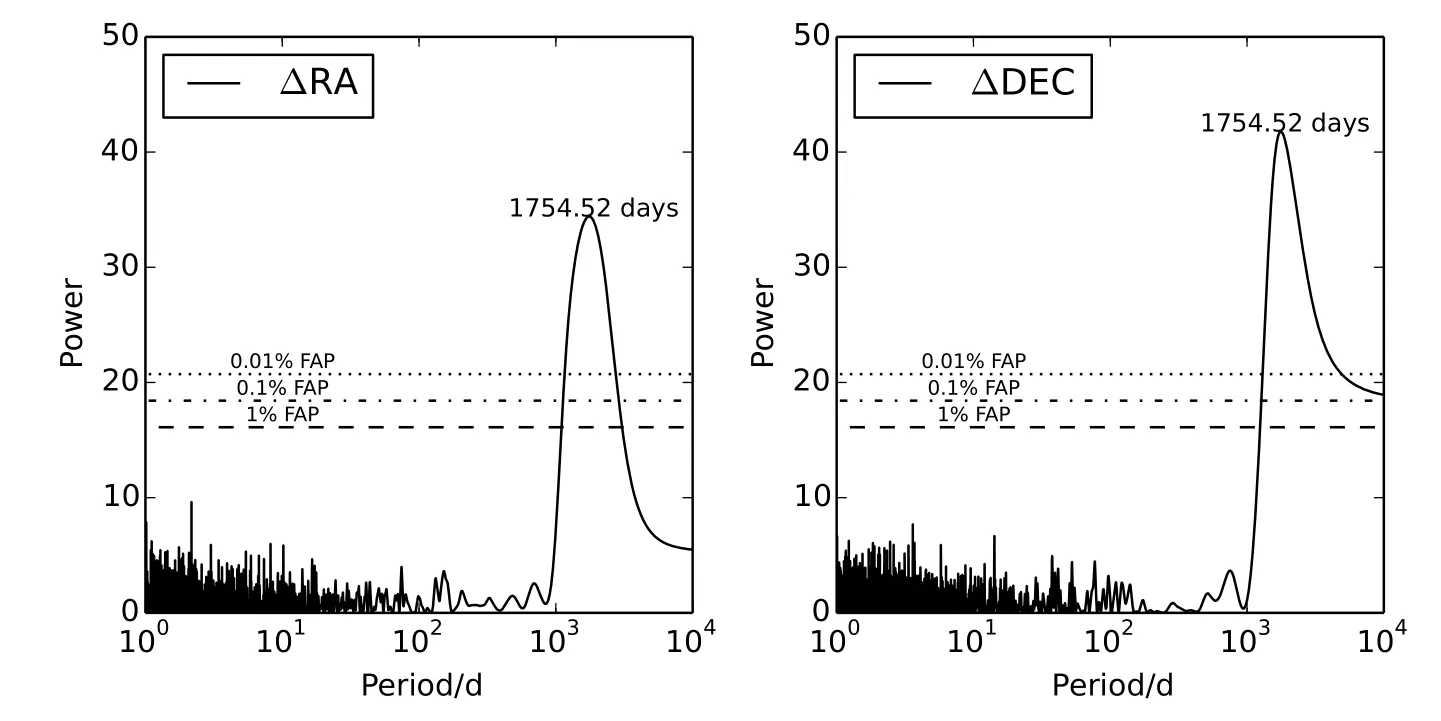
图4 αCentau ri A的模拟天体测量数据的Lom b-Scargle周期谱,其中存在一个1750 d左右的周期信号.虚线表示1%的FAP,点虚线表示0.1%的FAP,点线表示0.01%的FAP.Fig.4 The Lom b-Sarg le p eriodogram o fm ock astrom etric data o fαCen tau ri A.A 1750-day p eriod ex ists in the p eriodogram.The 1%,0.1%,and 0.01%o f FAP are ind icated by the dashed line,dot-dashed line, and dotted line,respectively.

图5 左:αCentau ri A的归一化天体测量拟合曲线和拟合行星b后的残差;右:αCentau ri A的天体测量法拟合 曲线Fig.5 Left:The norm a lized astrom etric cu rve ofαCen tau ri A and the residua l a fter fitting p lanet b; R ight:The astrom etric cu rve o fαCen tau ri A

4.2 HD 62509

HD 62509 b是一颗在2006年由Reffert等人通过视向速度法发现、围绕K 0III型主星HD 62509的系外行星[23].HD 62509 b的周期约590 d,半长径1.69 au,最小行星质量Mpsin i为2.9 MJupiter.生成模拟的天体测量数据,并结合Lick的视向速度实测数据[23],计算Lomb-Scargle周期谱,找到最强的周期信号,对周期信号进行轨道拟合.

由图6和图7的Lomb-Scargle周期谱可以看到Lick视向速度数据和模拟的天体测量数据中存在一个约590 d的周期信号,不同FAP对应的功率在图中表示.对HD 62509的Lick视向速度数据,结合模拟的天体测量数据通过(4)式,使用MCMC算法进行拟合,得到表2中拟合结果及拟合误差.由于结合了视向速度数据,天体测量观测中的升交点经度Ω和近星点角距ω可以唯一确定,不再存在±180°的不确定性.近星点时刻用特定时刻的平近点角M0表示,采取时刻为Lick首次视向速度观测时刻JD 2451808.39.图8和图9分别为归一化视向速度法拟合曲线及拟合残差、归一化天体测量法拟合曲线及拟合残差.

表2 HD 62509 b的拟合参数Tab le 2 The fitting param eters o f HD 62509 b

图6 HD 62509的Lick视向速度观测数据的Lom b-Scargle周期谱,其中存在一个590 d左右的周期信号.虚线表示1%的FAP,点虚线表示0.1%的FAP,点线表示0.01%的FAP.Fig.6 The Lom b-Sarg le p eriodogram of L ick rad ia l velocity(RV)data of HD 62509.A 590-day p eriod exists in the periodogram.The 1%,0.1%,and 0.01%of FAP are indicated by the dashed line,dot-dashed line,and dotted line,respectively.

图7 HD 62509的模拟天体测量数据的Lom b-Scargle周期谱,其中存在一个590 d左右的周期信号.虚线表示1%的FAP,点虚线表示0.1%的FAP,点线表示0.01%的FAP.Fig.7 The Lom b-Sarg le p eriodogram o f m ock astrom etric data of HD 62509.A 590-day period exists in the p eriodogram.The 1%,0.1%,and 0.01%o f FAP are ind icated by the dashed line,dot-dashed line,and dotted line,respectively.

图8 HD 62509的归一化视向速度拟合曲线和拟合行星b后的残差Fig.8 The norm a lized RV cu rve of HD 62509 and the residua l a fter fitting p lanet b

图9 左：HD 62509的归一化天体测量法拟合曲线和拟合行星b后的残差;右：HD 62509的天体测量法拟合曲线Fig.9 Left:The norm a lized astrom etric cu rve of HD 62509 and the residua l a fter fitting p lanet b;R igh t: The astrom etric cu rve of HD 62509

4.3 G J 876

GJ 876是距离地球4.689 pc[24]的M 4型恒星[25],通过长达20 yr的视向速度观测发现, GJ 876存在着4颗行星围绕其公转[26−30].GJ 876行星系统是距离地球最近的多行星系统,是首个发现存在轨道共振(Mean Motion Resonance,MMR)的行星系统[28],同时也是首个发现存在拉普拉斯共振的系外行星系统[30−32].

在GJ 876系统中,除去以约2 d周期围绕GJ 876公转的行星d外,行星c(周期约30 d)、行星b(周期约61 d)和行星e(周期约124 d)存在着4:2:1的拉普拉斯共振.由于GJ 876系统中行星与行星间的相互摄动非常强烈,传统的开普勒椭圆拟合无法很好拟合长达20 yr的视向速度观测数据.Laughlin等[33]和Rivera等[34]在2001年先后分别提出对GJ 876系统的N体积分牛顿动力学数值解,在传统的LM算法上加入N体积分算法,求出行星在特定时刻的轨道解,从而降低视向速度数据拟合的χ2.

而本文采取的是改进的开普勒椭圆拟合,采用文献[30]中表3的N体积分牛顿动力学数值求解得到的轨道根数,恒星质量为0.32 M⊙.为了与文献[30]中的结果比较,我们选取在JD 2450602.093至JD 2452428.093内生成52组模拟的天体测量数据,再对其进行改进的开普勒椭圆拟合.

对于使用开普勒椭圆拟合天体测量数据,需要拟合7个参数(α,e,i,Ω,ω,M0,mp),而对于存在2:1轨道共振的行星系统,近星点角距存在着快速的线性变化:˙ϖ= |j4|Cre|j4|−2cosϕ[35],其中ϕ为共振角,j4为共振角中的系数,Cr为含拉普拉斯系数的参数.对于处于平运动共振的行星,其共振角总是在一定范围内摆动,等式右边可以视为恒值,即位于2:1轨道共振的行星的近星点存在进动,因此可以额外增加变量˙ω共8个参数作为单行星的改进开普勒椭圆拟合,改进的开普勒椭圆拟合本质上是一个不断进动的开普勒椭圆拟合.根据文献[30]的表3,行星b和行星c的天体测量信号分别为298µas和58 µas,而行星d和行星e的天体测量信号分别只有0.28µas和9.64µas,远低于Gaia单次天体测量精度34.2µas[7],因此这里只对行星b和c进行共平面的改进开普勒椭圆拟合.

通过使用MCMC算法,最终得到表3和表4中行星b与行星c的拟合结果,可以看到使用改进的开普勒椭圆拟合有较好的拟合结果.由于我们并没有加入GJ 876的视向速度数据进行拟合,所以升交点经度Ω与近星点角距ω由近星点经度ϖ表示.图10为行星b和c的天体测量法时序拟合曲线及拟合残差,图11为行星b和c的天体测量法曲线及拟合残差.

表3 GJ 876 b的拟合参数Tab le 3 The fitting p aram eters o f G J 876 b

表4 GJ 876 c的拟合参数Tab le 4 The fitting param eters o f G J 876 c

图10 改进的开普勒拟合行星GJ 876 b和G J 876 c天体测量法时序曲线及拟合残差Fig.10 The m od ified K ep lerian astrom etric cu rve of GJ 876 b and G J 876 c and the fitting residua l

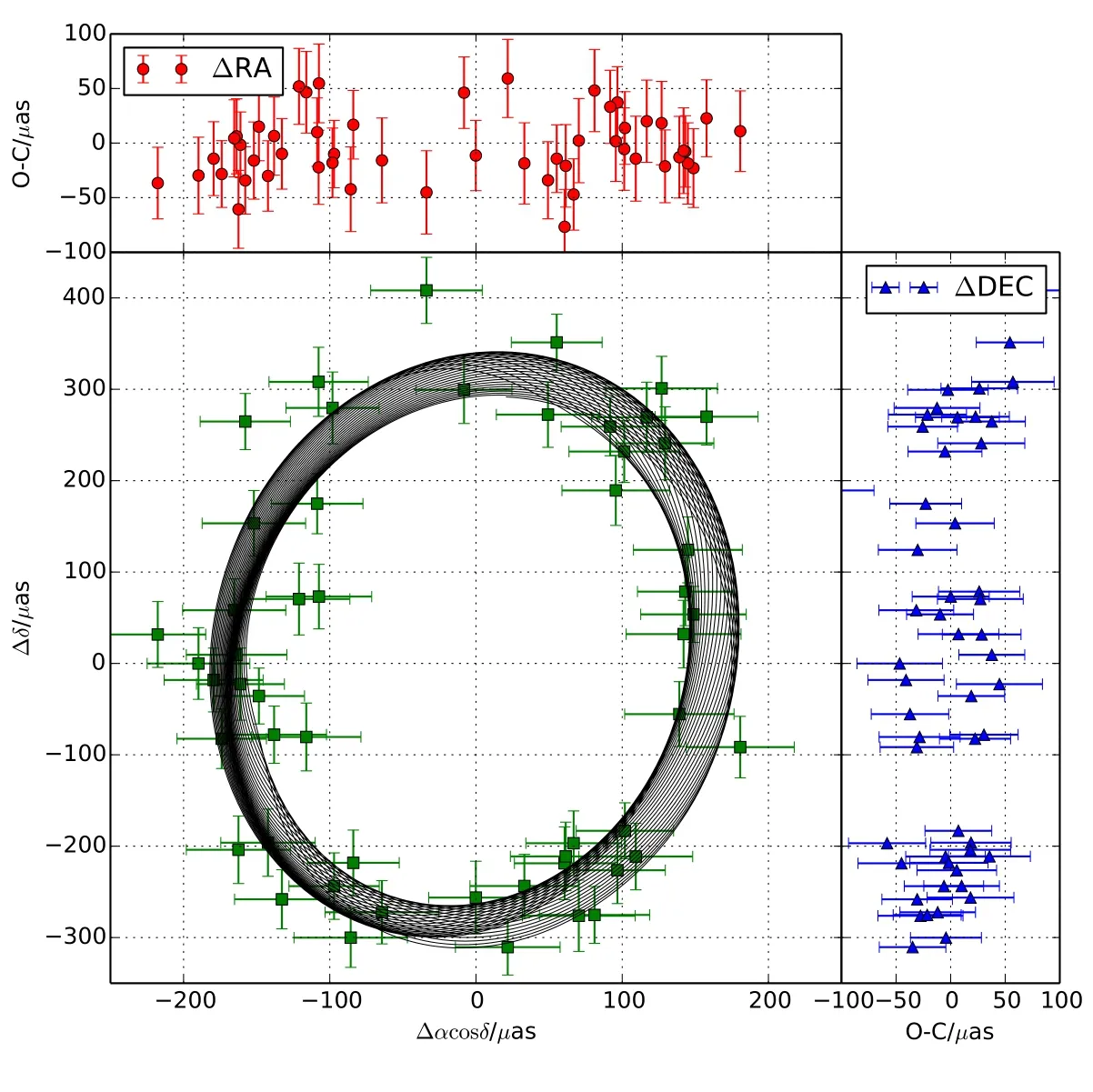
图11 行星G J 876 b和G J 876 c改进的开普勒拟合曲线及拟合残差Fig.11 The m od ified K ep lerian fitting cu rve o f G J 876 b and G J 876 c and the fitting residual

5 讨论

5.1 观测采样方案的影响

Ford曾针对SIM(Space Interferometer M ission)的观测方案讨论到,对于定点的天体测量观测,不同的观测采样方案会对行星探测效率有不同的影响[4].同时由于天体测量法探测系外行星首先要拟合出恒星的周年视差,而周年视差的周期为1 yr,天体测量法会降低轨道周期在1 yr附近行星的探测效率,因为围绕类太阳恒星的宜居带行星的轨道周期在1 yr左右,这对探测宜居带行星带来一定的困难[4].

5.2 天体物理噪声

由于恒星表面的耀斑、黑子、米粒组织和非径向对流等,会造成恒星星像的抖动,造成图像光心的偏移.这类影响是恒星自身所固有的,因此称为天体物理噪声.天体物理噪声对视向速度和天体测量法均有影响,对于平静稳定的低自转恒星,天体物理噪声对其视向速度造成3–5m/s的抖动,而对天体测量观测所造成的抖动的影响可由下式进行估计[36−41]:

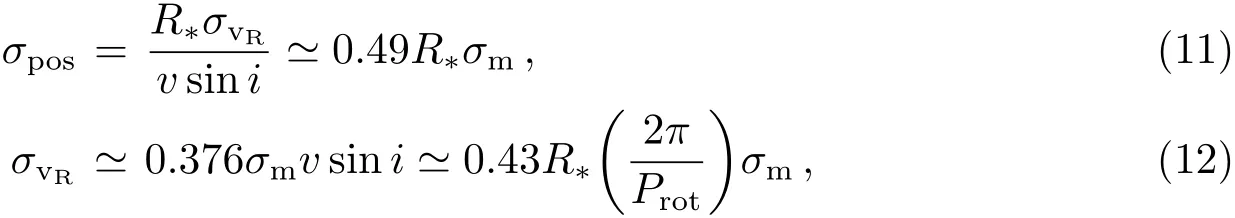
σpos、σvR和σm分别是天体测量法、视向速度和星等均方根值.R∗为恒星的半径, v sin i为恒星自转速度径向投影,Prot为恒星的自转周期.

5.3 视差和自行的加速项

恒星在银河系中围绕银心不断运动,太阳也在以约2.5亿年的周期围绕银心运动,视差和自行是由于恒星相对太阳的位置和运动引起的.由于银河系恒星运动的复杂性,视差和自行并不是不变的.恒星的视差与自行有如下变化[42]:

µ为恒星的总自行,vr为恒星的视向速度,A为天文单位.对于大多数恒星,短期内的天体测量观测中自行变化可以忽略,但对一些高自行的恒星,如Barnard星,必须考虑自行的加速项.

5.4 行星间引力作用

对于一些行星与行星间引力作用强烈的系统,行星间摄动在观测时段内造成的天体测量法变化较大,是不适合用(3)式进行轨道拟合的,例如GJ 876系统[43−46]、55 Cnc系统[47−49]等.对于这类行星间引力作用强烈的行星系统,传统的开普勒轨道解不能很好地拟合观测数据.对于存在轨道共振的系统,对于算例所示的GJ 876系统,改进的开普勒椭圆拟合有一定实用意义,但此方法不能普适于非共振的行星系统,因此求解N体积分的牛顿动力学数值轨道解有其必要性.

6 总结与展望

在本文中,我们针对αCentauri A、HD 62509和GJ 876系统,基于Gaia单次天体测量法精度生成多组对应的仿真数据,使用Lomb-Scargle周期谱分析行星轨道周期信号,进而采用MCMC算法对3个行星系统进行轨道反演,解算结果与行星的初始参数相吻合.

目前发现的大多数系外行星所造成的天体测量信号小于1 mas,而地面的天体测量法精度难以达到1 m as以下,但随着高精度的空间天体测量卫星的升空,未来将有大量通过天体测量法被发现的系外行星.哈勃空间望远镜(HST)上的FGS能以1 m as的天体测量法精度进行窄角天体测量法[50],詹姆斯韦伯空间望远镜(JWST)作为哈勃望远镜的继任者,也会安装上FGS.Gaia在释放第1批数据后,预期可发现大量长周期的类木行星.STEP预期有能力以1µas的窄角天体测量法精度发现距离太阳15 pc内的类地行星.在2016年Gaia公布其观测数据后,我们可以利用本文的行星3维轨道拟合方法来对Gaia的数据进行处理,以发现更多的系外行星并开展科学研究.另外在将来的工作中,我们还将对行星轨道的拟合方法做进一步改进,在行星开普勒解的基础上发展N体积分动力学数值轨道解,这将有助于我们更好地了解系外行星系统.

[1]M ayor M,Q ueloz D.Natu re,1995,378:355

[2]M u terspaugh M W,Lane B F,K u lkarni S R,et a l.A J,2010,140:1657

[3]Pou rbaix D,Jorissen A.A&AS,2000,145:161

[4]Ford E B.PASP,2004,116:1083

[5]M akarov V V,Beichm an C A,Catanzarite J H,et a l.A p JL,2009,707:L 73

[6]Perrym an M A C,Lindegren L,K ovalevsky J,et al.A&A,1997,323:L 49

[7]Perrym an M,Hartm an J,Lindegren L.A p J,2014,797:14

[8]Perrym an M.The Exop lanet Handbook.New York:Cam b ridge University P ress,2011

[9]K ovalevsky J,Seidelm ann P K.Fundam en tals o f A strom etry.New York:Cam b ridge Un iversity P ress, 2004

[10]Cumm ing A,M arcy G W,Bu tler R P.A p J,1999,526:890

[11]Lom b N R.A&SS,1976,39:447

[12]Scarg le J D.A p J,1982,263:835

[13]P ressW H,Teukolsky S A,Vetterling W T,et al.Num erical Recipes.New York:Cam b ridge University P ress,1992

[14]Ford E B.A p J,2006,642:505

[15]G regory P.Bayesian Logical Data Analysis for the Physical Sciences:A Com parative App roach w ith M athem atica®Supp ort.New York:Cam b ridge Un iversity P ress,2005

[16]G regory P C.M NRAS,2007,381:1607

[17]G regory P C.M NRAS,2007,374:1321

[18]Lattanzi M G,Spagna A,Sozzetti A,et a l.M NRAS,2000,317:211

[19]Dum usque X,Pep e F,Lov is C,et a l.Natu re,2012,491:207

[20]Ra jpau l V,A igrain S,Roberts S.M NRAS,2016,456:L 6

[21]Hoffleit D,Jaschek C.The B right Star Catalogue.5th ed.New Haven:Yale University Observatory, 1991

[22]K ervella P,Th´even in F,S´egransan D,et a l.A&A,2003,404:1087

[23]Reffert S,Quirrenbach A,M itchell D S,et al.Ap J,2006,652:661

[24]Van Leeuw en F.A&A,2007,474:653

[25]von B raun K,Boya jian T S,van Belle G T,et a l.M NRAS,2014,438:2413

[26]M arcy G W,Butler R P,Vogt S S,et al.Ap JL,1998,505:147

[27]Delfosse X,Forveille T,Beuzit J L,et a l.arX iv:astro-ph/9812008,1998

[28]M arcy G W,Butler R P,Fischer D,et al.A p J,2001,556:296

[29]R ivera E J,Lissauer J J,Bu tler R P,et a l.A p J,2005,634:625

[30]Rivera E J,Laugh lin G,Bu tler R P,et al.Ap J,2010,719:890

[31]W ang S,Ji J,Zhou J L.A p J,2012,753:170

[32]W ang S,Ji J.A p J,2014,795:85

[33]Laugh lin G,Cham bers J E.A p JL,2001,551:109

[34]R ivera E J,Lissauer J J.A p J,2001,558:392

[35]M u rray C D,Derm ott S F.So lar System D ynam ics.New York:Cam b ridge Un iversity P ress,1999

[36]Saar S H,Donahue R A.A p J,1997,485:319

[37]Queloz D.11th Cam b ridge W orkshop on Coo l Stars,Stellar System s and the Sun,2001,223:59

[38]Hen ry G W,Donahue R A,Ba liunas S L.A p JL,2002,577:111

[39]Saar S,Seager S.arX iv:astro-ph/0305436,2003

[40]Hatzes A P.AN,2002,323:392

[41]Pau lson D B,Coch ran W D,Hatzes A P.AJ,2004,127:3579

[42]D rav ins D,G u llberg D,Lindegren L,et a l.ASPC,1999,185:41

[43]Ji J,Li G,Liu L.A p J,2002,572:1041

[44]Ji J,Liu L,K inosh ita H,et a l.A p JL,2003,591:57

[45]季江徽,刘林.天文学报,2006,47:402

[46]Ji J H,Liu L.ChA&A,2007,31:187

[47]Ji J H,K inoshita H,Liu L,et al.A p JL,2003,585:139

[48]Ji J H,K inoshita H,Liu L,et al.RAA,2009,9:703

[49]Ji J H,Lin L,Zhou J L,et a l.ChA&A,2003,27:127

[50]Nelan E P,Lup ie O L,M cA rthu r B,et a l.SP IE,1998:237

A nalogue Sim u lation and O rb ital Solving A lgorithm of A strom etric Exop lanet Detection

HUANG Ping-hui1,2,3JIJiang-hui1,2

(1 Pu rp le M oun tain O bserva to ry,Chinese A cadem y o f Scien ces,Nan jing 210008) (2 K ey Labo ra to ry o f P laneta ry Scien ces,Chinese A cadem y o f Scien ces,Nan jing 210008) (3 Un iversity o f Chinese A cadem y o f Scien ces,Beijing 100049)

Astrometry is an effectivemethod to detect exoplanets.It hasmany advantages that other detectionmethods do not bear,such as providing three dimensional planetary orbit and determ ining the planetarymass.Astrometry w illenrich the sam ple of exop lanets.As the high-precision astrometric satellite Gaia(G lobal Astrom etry interferometer for Astrophysics)was launched in 2013,therew illbe abundant long-period Jupiter-size p lanets to be discovered by Gaia.In this paper,we specify theαCentauri A,HD 62509,and GJ 876 systems,and generate the synthetic astrometric data w ith the single astrom etric precision of Gaia.Then we use the Lomb-Scargle periodogram to analyse the signature of planets and the Markov Chain Monte Carlo(MCMC)algorithm to fit the orbit of p lanets.The simulation results are well coincide w ith the initial solutions.

astrometry,planets and satellites:evolution,astrometric satellites:Hipparcos,Gaia,m ethods:Lomb-Scargle periodogram,M arkov Chain M onte Carlo(MCMC)

P144;

A

10.15940/j.cnki.0001-5245.2016.05.007

2016-01-29收到原稿,2016-02-27收到修改稿

∗国家自然科学基金项目(11273068,11473073)、中国科学院战略性先导科技专项(XDB09000000)、中国科学院空间科学战略性先导科技专项(XDA 04060900)、中国科学院新兴与交叉学科布局试点项目(KJZD-EW-Z001)及紫金山天文台小行星基金会资助

†phhuang@pmo.ac.cn

‡jijh@pm o.ac.cn