北斗卫星单系统精密定轨方法对比分析

刘伟平 郝金明 邓科 陈逸伦

(1信息工程大学导航与空天目标工程学院 郑州 450001) (2北斗导航应用技术河南省协同创新中心 郑州 450001)

北斗卫星单系统精密定轨方法对比分析

刘伟平1,2†郝金明1,2邓科1陈逸伦1

(1信息工程大学导航与空天目标工程学院 郑州 450001) (2北斗导航应用技术河南省协同创新中心 郑州 450001)

提出了联合使用载波相位和相位平滑伪距实现北斗卫星双差动力法精密定轨,给出了北斗卫星非差动力法和双差动力法精密定轨的数据处理流程,分析了两种方法的异同.结合实测数据,对比了两种方法的实际定轨效果,结果表明:一定测站布局下,利用两种方法,GEO(Geostationary Earth O rbit Satellite)卫星3维精密定轨精度均能达到1m左右量级,IGSO(Inclined Geosynchronous Earth O rbit Satellite)和M EO(M edium Earth O rbit Satellite)卫星优于0.5 m,3类卫星的径向定轨精度均优于10 cm.较之非差动力法,双差动力法对GEO卫星精密定轨精度具有一定的改善作用,两者在IGSO卫星精密定轨上效果基本相当,但在MEO卫星定轨上,非差动力法结果更优.

天体力学,航天器,方法:数据分析

1 引言

在导航卫星单系统精密定轨中,通常使用经典的动力学法[1].根据观测量组差方式的不同,又可细分为非差动力法和双差动力法[2].非差动力法使用非差观测量进行精密定轨,无需组差,不损失观测信息,观测量间的独立性较好,可规避复杂的相关权问题,能够同时估计轨道和钟差参数,算法实现简单明了,其缺点是对误差改正模型的精度有较高要求,并且需要同时估计大量参数,会在一定程度上影响算法的数值稳定性[3];双差动力法在定轨中使用双差观测量,可消除或减弱大部分误差源的影响,并保持模糊度的整数特性,同时能够消除大量的钟差参数,从而减少待估参数个数,有助于参数估计的数值稳定性,其缺点是组差处理损失了观测信息,增加了观测量之间的相关性[4].总之,在导航卫星精密定轨中,非差动力法和双差动力法各有利弊,两种方法在主要的导航卫星精密定轨软件中都得到了广泛应用,如Bernese(Bernese GPS Software)、GAM IT(GPS Analysis at M IT)等软件主要采用了双差数据处理模式,而EPOS(Earth Parameter and Orbit System)、PANDA(Positioning and Navigation Data Analysis)等软件则主要采用了非差数据处理模式.

2012年底,北斗系统建成了由5颗GEO、5颗IGSO和4颗MEO构成的区域星座,开始为亚太地区提供无源导航服务[5−7].为推动北斗系统在高精度领域的应用发展,已有文献分别探讨了北斗系统的非差动力法和双差动力法精密定轨方法.Ge等[8]研究了北斗系统非差精密定轨方法,GEO和IGSO卫星3维定轨精度分别达到了3.3 m和0.5 m; Zhao等[9]基于武汉大学建立的北斗卫星观测实验网,实现了径向精度优于10 cm的北斗卫星非差动力法精密定轨;He等[10]分析了观测几何构形、模糊度固定等对北斗非差动力法精密定轨精度的影响;宋小勇[11]研究了基于双差伪距的北斗卫星精密定轨方法,并对基于载波相位的北斗区域定轨效果进行了分析讨论;Zhu等[12]利用国内测站及部分IGS(International Global Navigation Satellite System Service)多系统测站的实测数据,分析了北斗卫星双差法精密定轨的效果.此外，国内外相关学者还研究了基于多系统数据融合处理的北斗卫星精密定轨方法[13−19].本文主要探讨北斗单系统精密定轨方法,对这类方法不再赘述.

从目前的研究来看,虽然北斗系统的非差动力法和双差动力法精密定轨方法均有文献论及,但是两种方法在北斗系统中应用效果的分析对比还鲜有文献讨论,而这种分析对比对北斗系统精密定轨处理策略的选择以及后续精密定轨方法的改进均有重要意义.有鉴于此,本文首先介绍了北斗系统的两种精密定轨方法,分别给出了两种方法的数据处理流程,在此基础上,结合实测数据,分析对比了两种方法的实际应用效果.

2 北斗卫星非差动力法精密定轨

利用非差动力法进行北斗卫星精密定轨的数据处理流程如下:首先,对载波相位和伪距进行数据预处理,并利用广播星历提供的初值进行轨道积分,在此基础上,建立相位和伪距的非差观测方程;而后,开始组建法方程,为提高参数估计的效率,先对钟差等历元参数进行预消除,待完成轨道估计之后,再回代求解钟差等预消除参数;最后,对残差进行分析,剔除问题测站和卫星,并基于残差分析结果,对观测数据进行再编辑.迭代进行上述定轨过程,直到残差达到精度指标要求,输出最终定轨结果.整个数据处理流程见图1.需要说明的是,以上处理中还需要使用一些外部辅助信息,如测站先验坐标、地球自转参数、天线类型等.

3 北斗卫星双差动力法精密定轨

研究表明,由于北斗GEO卫星切向轨道分量与双差模糊度存在强相关性[20],如果采用经典双差动力法,仅依靠载波相位数据,无法取得足够精度的北斗系统精密定轨结果[2].本文联合载波相位和伪距观测量实现北斗卫星双差动力法精密定轨,为了进一步提高定轨结果的精度,还对伪距进行了相位平滑处理.线性化后的观测方程如下:

以观测方程(1)–(2)式为基础,利用最小二乘参数估计方法,即可进行北斗卫星的双差动力法精密轨道确定,具体处理流程为:首先,分别对载波相位和伪距观测量进行预处理,主要是剔除伪距和载波相位的粗差,并对载波相位进行周跳探测和修复;然后,利用相位数据对伪距进行平滑处理,以提高伪距的观测精度;其次,选取独立基线,形成单差观测量,并利用三差的方法对相位数据再次进行周跳探测等处理;然后,由广播星历提供初值进行轨道积分,结合以上的观测数据,组建相位和平滑伪距的双差观测方程,并进行参数估计,获得模糊度浮点解;分析参数估计的残差,进行问题测站和卫星的剔除,并据此进行观测数据的再编辑,迭代进行以上的轨道确定过程,直到残差达到精度指标要求;然后进行双差模糊度固定;最后,引入固定的模糊度,重新进行参数估计,得到整数解,并输出定轨结果.整个数据处理流程见图2.

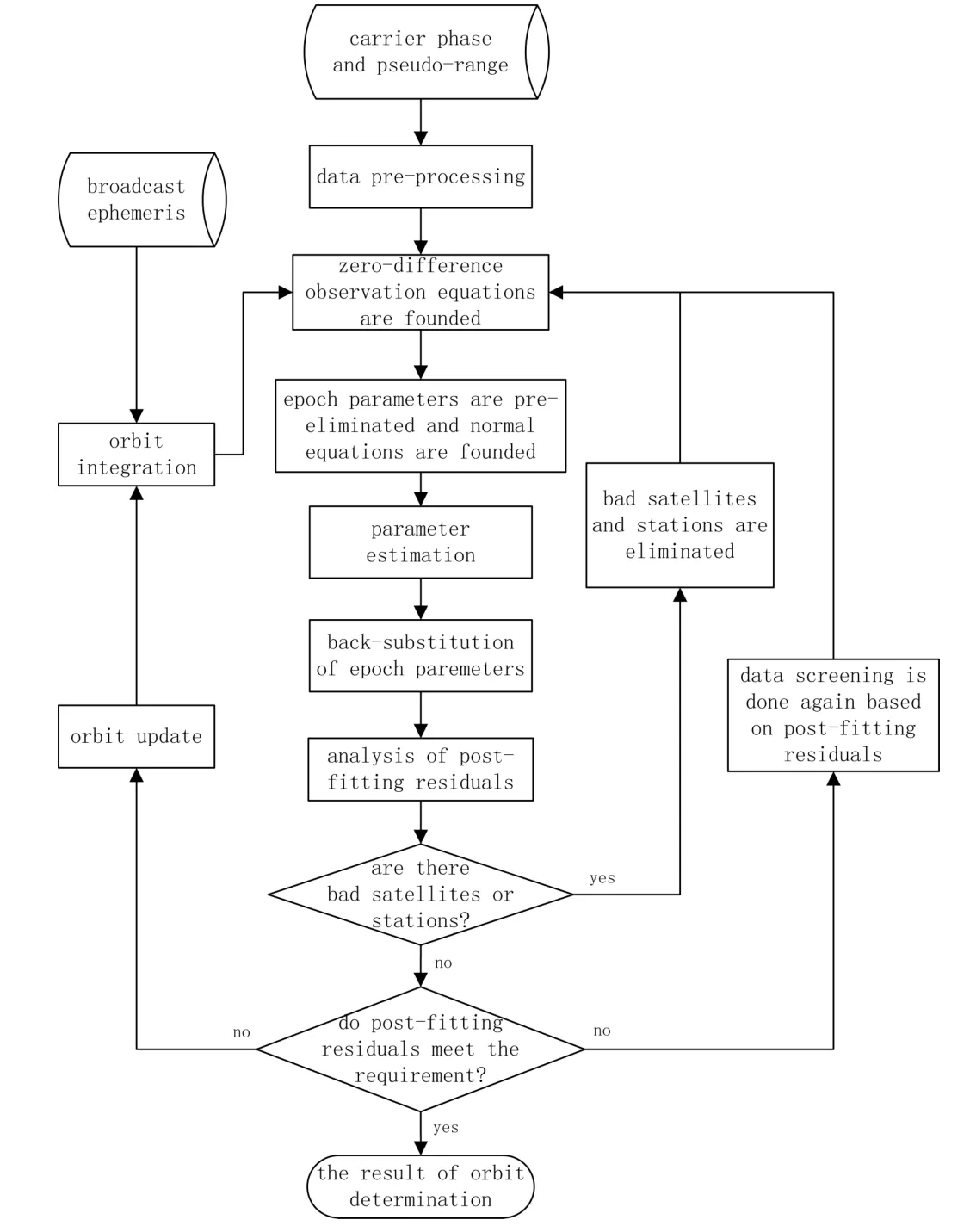
图1 北斗卫星非差动力法精密定轨数据处理流程图Fig.1 The flow chart o f p recise orb it determ ination for BeiDou satellites by using the zero-d ifference dynam ic m ethod

图2 北斗卫星双差动力法精密定轨数据处理流程图Fig.2 The flow chart o f p recise orbit determ ination for BeiDou satellites by using the doub le-d ifference dynam ic m ethod

4 算例分析

为了对比北斗卫星非差动力法和双差动力法精密定轨的精度差异,这里采用2013年年积日161–171共11 d数据进行精密定轨实验,测站分布见图3,其中,12个测站来自IGS多系统实验网M-GEX(M ulti-GNSS EXperiment),12个测站来自武汉大学北斗卫星观测实验网BETS(BeiDou Experimental Tracking Stations),分别以圆点和方框标示.

实验中以每3 d数据为一个定轨弧段,共形成9个定轨弧段及8个重叠弧段,统计重叠弧段上的轨道差值,以考察精密定轨效果.采用如下两种方案进行解算(具体处理策略见表1):方案1(S1)为非差动力法精密定轨;方案2(S2)为双差动力法精密定轨.

图3 测站分布图Fig.3 The station layou t

表1 定轨策略Tab le 1 The strategy o f orb it d eterm ination

为了增强对比性,两种方案中模糊度均采用了浮点解.需要说明的是,这里评定轨道精度使用了重叠弧段,这是一种检验内符合精度的手段.之所以没有采用激光测距评估或与其他组织提供的精密轨道比对评估等外符合精度评估方法,主要是由于:对于前者,不是所有北斗卫星都具有全球激光测距数据,因此使用这种方法进行分析,不能反映整个星座的定轨效果;而对于后者,其他组织提供的精密轨道要么使用非差法,要么使用双差法,用其作为标准检测非差动力法或双差动力法的定轨效果,会由于方法之间的自洽等因素影响评估的客观性.因此,本文选用了重叠弧段进行精度分析,更方便对比非差动力法与双差动力法本身的定轨效果.

表2和图4给出了两种方案中各颗卫星在所有重叠弧段上径向(R)、切向(T)、法向(N)和3维方向(P)轨道差值的平均RMS(Root M ean Square).

表2 北斗卫星非差动力法与双差动力法定轨精度统计表Tab le 2 The orb it d eterm ination p recision statistics o f B eiD ou satellites w ith the zero-d ifferen ce and doub le-d ifferen ce dynam ic m ethod s

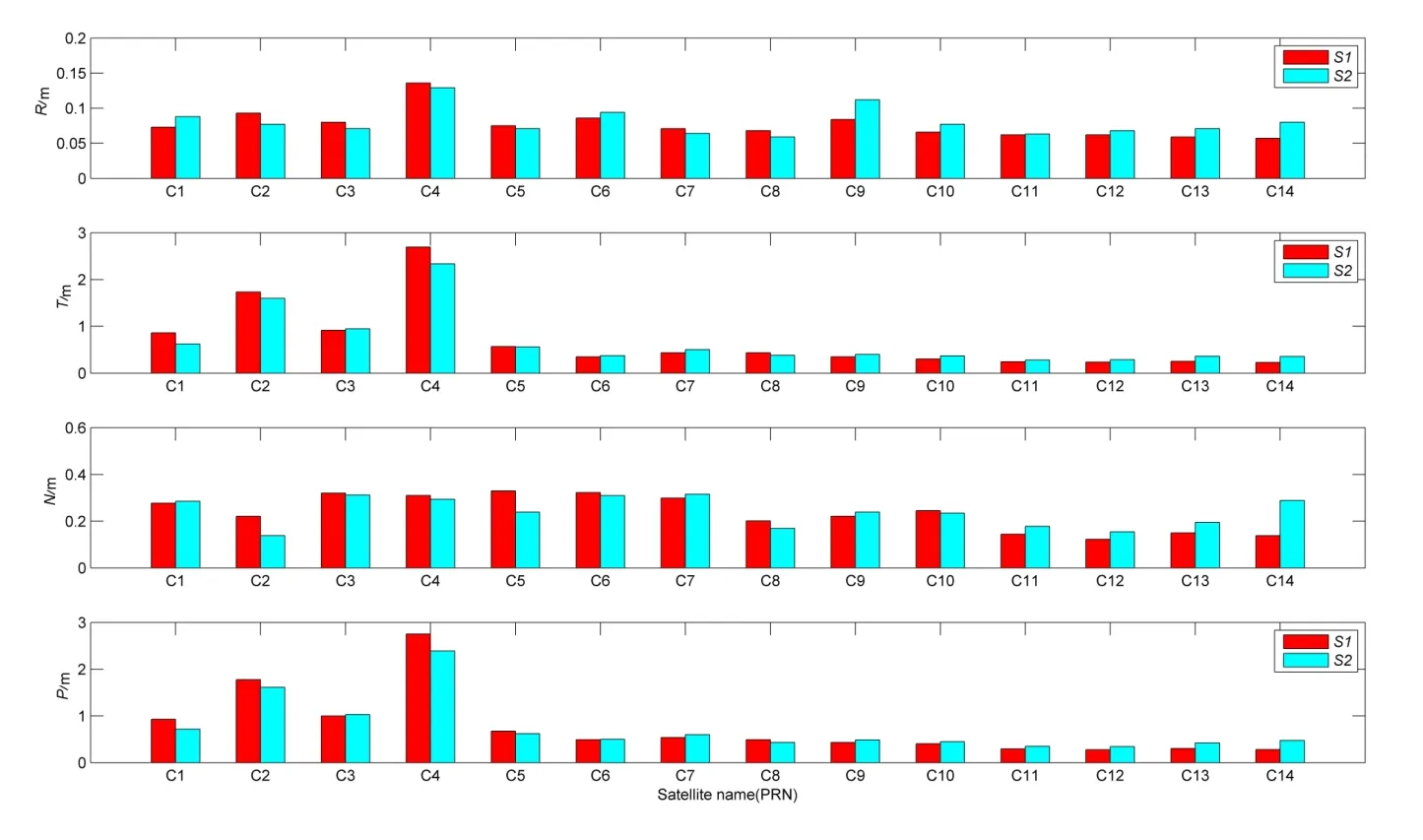
图4北斗卫星非差动力法与双差动力法定轨精度对比图Fig.4 Com parison of the orbit determ ination p recision o f BeiDou satellites w ith the zero-d ifference and doub le-d ifference dynam ic m ethods

图5 、图6以年积日165、166、167及166、167、168两组3 d的定轨弧段为例,分别给出C1(GEO)、C6(IGSO)、C11(MEO)星在两种方法中重叠弧段轨道差值的变化情况.

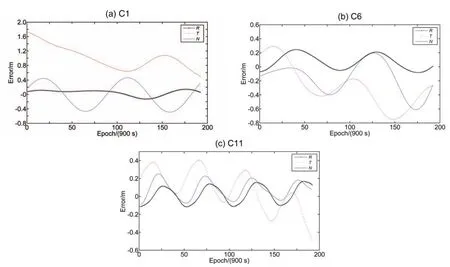
图5 北斗卫星非差动力法精密定轨重叠弧段轨道差值变化情况Fig.5 The overlapped-arc errors of BeiDou satellite orbit determ ination by using the zero-d ifference dynam ic m ethod

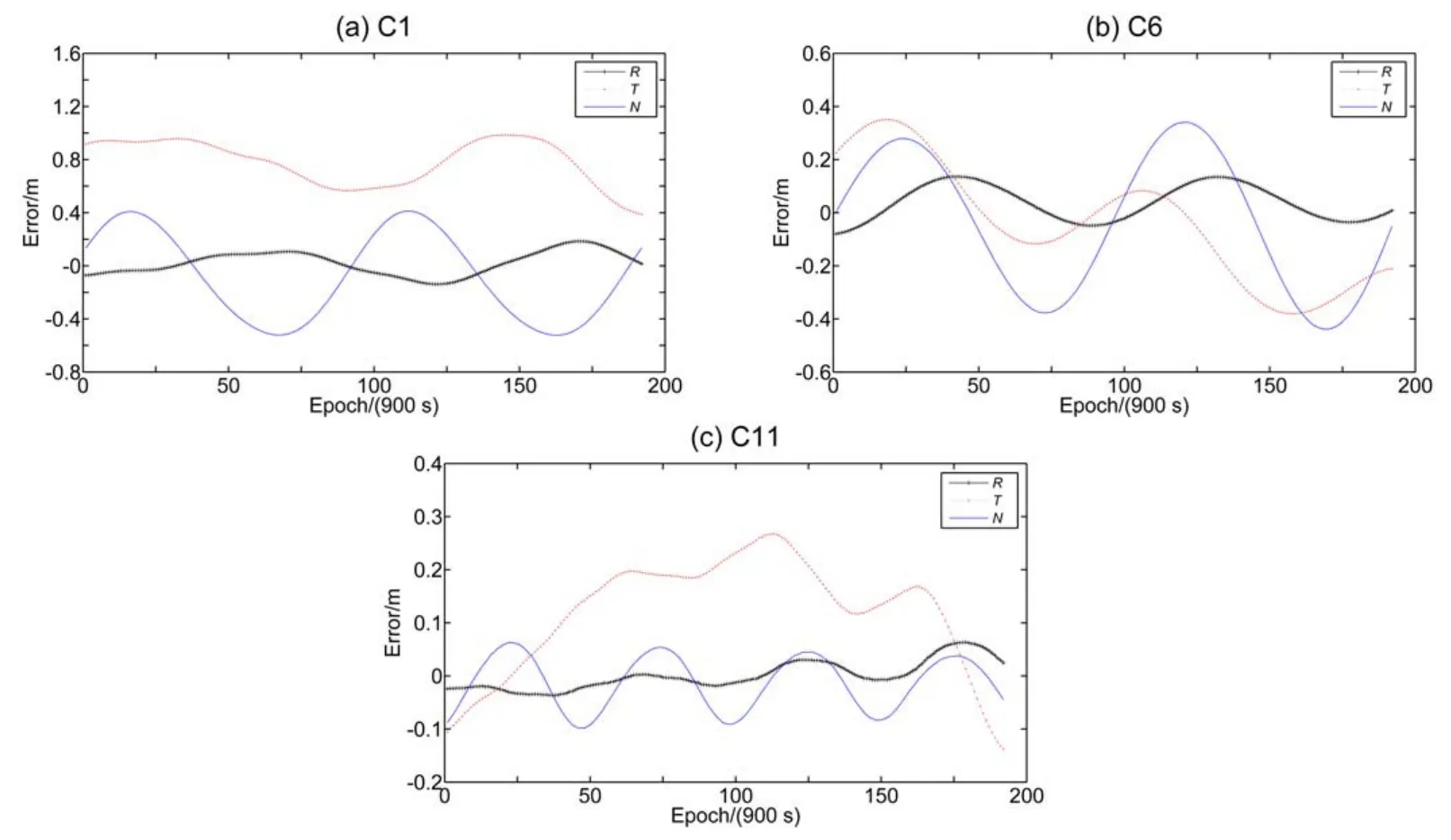
图6 北斗卫星双差动力法精密定轨重叠弧段轨道差值变化情况Fig.6 The overlapp ed-arc errors of BeiDou satellite orb it determ ination by using the doub le-d ifference dynam ic m ethod

由表2和图4的结果可见:

(1)平均来讲,非差动力法精密定轨中,GEO、IGSO和MEO卫星3维定轨精度分别达到1.426m、0.471m、0.289m,3者的径向定轨精度都优于10 cm;双差动力法精密定轨中,GEO、IGSO和MEO卫星3维定轨精度分别达到1.273 m、0.492 m、0.397 m,径向精度也均优于10 cm.无论非差动力法还是双差动力法,GEO卫星3维精密定轨精度均能达到1m左右量级,IGSO和MEO卫星优于0.5m,3类卫星的径向定轨精度均优于10 cm.在两类方法中,GEO卫星定轨精度明显低于IGSO和MEO卫星,3类卫星R、N方向定轨精度基本相当,但GEO卫星T方向的定轨精度则明显较差,主要原因是:GEO卫星对地静止,造成切向轨道分量与模糊度参数较难分离.此外,C4卫星由于观测几何结构较差,在两类方法中,定轨精度明显低于同类卫星.

(2)进一步比较分析发现,较之非差动力法,双差动力法对GEO卫星精密定轨精度具有一定的改善作用,两者在IGSO卫星精密定轨上效果基本相当,但在MEO卫星定轨上,非差动力法结果更优.分析其原因,认为是:双差法通过站星间组差,消去了卫星和测站的钟差参数,有效地减少了参数估计中的待估参数,有益于提高GEO卫星的轨道解算精度.但是,对于MEO卫星,由于在轨卫星仅有4颗且全球运行,地面测站的区域分布使其双差观测量数目受限,非差法由于具有更高的数据利用率,定轨精度更优.IGSO卫星虽然也有类似问题,但其运行仅限于亚太区域,而该区域中测站分布密集,能够形成更多的双差观测量,因此其双差法精密定轨精度仅略低于非差法,基本相当.

由图5和图6可见,在两类方法中,IGSO和MEO卫星轨道误差变化趋势基本相当, GEO卫星切向误差明显较大,对比两类方法的结果可见,同类卫星轨道误差变化基本在同一量级水平.

5 结语

本文给出了北斗系统非差动力法和双差动力法精密定轨的数据处理流程,并提出了联合使用载波相位和相位平滑伪距实现北斗卫星双差动力法精密定轨,在此基础上,对比了两种单系统精密定轨方法的异同,利用实测数据,分析对比了两种方法的定轨效果.结果表明:无论非差动力法还是双差动力法,在文中算例的测站分布条件下,GEO卫星3维精密定轨精度均能达到1 m左右量级,IGSO和MEO卫星优于0.5 m,3类卫星的径向定轨精度均优于10 cm,C4星由于观测结构较差,定轨精度明显低于同类卫星.较之非差动力法,双差动力法对GEO卫星精密定轨精度具有一定的改善作用,两者在IGSO卫星精密定轨上效果基本相当,但在MEO卫星定轨上,非差动力法结果更优,以上结果是由双差动力法和非差动力法的不同解算模式、3类卫星的不同运动特点及区域测站布局共同决定的.值得注意的是,由于GEO卫星对地静止,造成切向轨道分量与模糊度参数较难分离,两类方法中GEO卫星切向定轨精度均明显低于IGSO和MEO卫星,有必要研究适当方法以进一步改进GEO卫星切向定轨精度.

[1]葛茂荣.GPS卫星精密定轨理论及软件研究.武汉:武汉测绘科技大学,1995:37-55

[2]刘伟平.北斗卫星导航系统精密轨道确定方法研究.郑州:信息工程大学,2014:36

[3]刘伟平,郝金明,于合理,等.大地测量与地球动力学,2014,34:169

[4]刘伟平,郝金明,于合理,等.测绘通报,2014:5

[5]杨元喜.测绘学报,2010,39:1

[6]中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件2.0.北京,2013:1-10

[7]中国卫星导航系统管理办公室.北斗卫星导航系统发展报告2.2.北京,2013:1-5

[8]Ge M R,Zhang H P,Jia X L,et a l.GPSW,2012,1:29

[9]Zhao Q L,G uo J,Li M,et a l．JGeod,2013,87:475

[10]He L N,G e M R,W ang J X,et a l.Sensors,2013,13:2911

[11]宋小勇.COM PASS导航系统卫星定轨研究.西安:长安大学,2009:1-20

[12]Zhu J,W ang J S,Zeng G,et a l.Ch ina Satellite Nav igation Con ference 2013 P roceed ings,2013:77-88

[13]Liu Y,Lou Y D,Shi C,et a l.Ch ina Satellite Nav igation Con ference 2013 P roceed ings,2013:173-186

[14]M ontenb ruck O,Hausch ild A,Steigenberger P,et al．GPS Solu tions,2013,17:211

[15]Steigenberger P,Hugentob ler U,Hausch ild A,et al．JGeod,2013,87:515

[16]施闯,赵齐乐,李敏,等.中国科学:地球科学,2012,42:854

[17]LiM,Zhao Q L,Sh i C,et a l.P recise O rb it Determ ination o f Beidou Satellites by Beidou/GPS.Ch ina Satellite Navigation Con ference,Guangzhou,M ay 15-19,2012

[18]刘伟平,郝金明,李建文,等.测绘科学技术学报,2013,30:247

[19]刘伟平,郝金明,李建文,等.测绘学报,2014,43:1132

[20]孙保琪.基于三频数据的Com pass卫星精密定轨．武汉:中国科学院测量与地球物理研究院,2010:1-10

Com parison and Analysis of BeiDou Satellite Single-system P recise Orbit Determ ination

LIUWei-ping1,2HAO Jin-m ing1,2DENG Ke1CHEN Yi-lun1

(1 School of Navigation and Aerospace Engineering,In form ation Engineering Un iversity, Zhengzhou 450001) (2 Beidou Navigation Techno logy Co llaborative Innovation Cen ter o f Henan,Zhengzhou 450001)

Themethod of double-difference dynam ic precise orbit determ ination for BeiDou satellites by using both carrier phase and smoothed pseudo-range is presented. The data processing flowsof zero-difference and double-difference dynam ic precise orbit determ ination for BeiDou satellites are presented.And the twomethods are analyzed. The precision of two methods is compared based on the real data.The results show that in the condition of stations layout and by using the two methods,the threedimension precision of GEO(Geostationary Earth Orbit Satellite)can reach about 1 m,and those of IGSO(Inclined Geosynchronous Earth Orbit Satellite)and MEO (Medium Earth Orbit Satellite)can be better than 0.5m.And the radial precision of the three kinds of orbit satellites can be all better than 10 cm.Compared w ith the zero-difference dynam icmethod,the orbit precision of GEO is better w ith the doubledifference dynam icmethod,and that of IGSO is comparable,but that ofMEO isworse.

celestialmechanics,space vehicles,methods:data analysis

P135;

A

10.15940/j.cnki.0001-5245.2016.05.004

2016-02-01收到原稿,2016-03-21收到修改稿

‡lw pchxy@sina.com