基于Bayesian方法的参数估计和异常值检测

尚　华，冯　牧，张贝贝

(1. 首都经济贸易大学 统计学院 北京 100070; 2. 中国科学技术大学 管理学院,安徽 合肥 230000)



基于Bayesian方法的参数估计和异常值检测

尚华1，冯牧2，张贝贝1

(1. 首都经济贸易大学 统计学院 北京 100070; 2. 中国科学技术大学 管理学院,安徽 合肥 230000)

摘要：异常值检测是当前数据分析研究中的一个重要研究领域。模型中的异常值会直接影响建模、参数的估计、预测等问题。基于模型的异常值检测，传统的做法是先对模型参数进行估计，再进行异常值检测。而异常值的存在会影响参数估计，从而导致下一步异常值检测的不可靠；反之异常值检测也会影响参数估计。针对这些不足之处，提出了基于Bayesian方法的参数估计和异常值检测，此方法可以将参数估计和异常值检测同时实现，具体做法是在线性回归模型中引入识别变量，基于Gibbs抽样算法，给出识别变量后验概率的计算方法，通过比较这些识别变量的后验概率进行异常值定位，同时给出参数的估算方法。通过大量的模拟实验，结果表明，与传统方法相比，提出的方法对异常值更灵敏。

关键词：线性回归；识别变量；参数估计；异常值；Bayesian方法；Gibbs抽样

0引言

对现代统计数据分析来说，异常值是一个普遍存在的问题。一般来说，异常值是指那些不同于数据中大部分数据的一个或多个观察值。在线性回归中，把偏离线性模式的观测值定义为异常值。Hampel等[1]认为，数据中包含10% 的异常值是很正常的。Hubert[2]和McCann-Welsh[3]认为数据中包含0.25n(n为数据量)个异常值是一个污染上界。

在应用背景下，回归分析是一个重要的统计工具。在回归技术中，一般采用最小二乘估计(ordinary least squares,OLS)，这是因为它的传统性和易计算性。然而由于异常值的出现，会使得用最小二乘估计的参数出现很大的偏差甚至错误，若再用于预测，可能会产生误导性的结论。另外，在很多实际情况下，可能对异常值本身感兴趣，例如银行诈骗、肿瘤监测以及报警系统等。不仅响应变量可能是异常值，解释变量也可能是异常值(杠杆点)。这2类异常值都会使得传统的最小二乘估计不可信。这里我们只讨论响应变量是异常值的情况。

基于模型的异常值检测一般分为2步：第1步对模型中的参数进行估计；第2步对残差进行评价，过大残差对应的观测值为异常值。为减小异常值对参数估计的影响，有很多稳健估计方法，例如最小截断二乘法的估计[4](least trimmed squares，LTS)、M-估计(minimum)[5]和S-估计(solution)[6]等。但是，参数估计与异常值检测之间相互影响[7-8]。若第1步参数估计得不稳健，会使得第2步异常值检测的正确率降低；反之，异常值检测的精度也能影响参数估计的稳健性。

本文要探讨的是用Bayesian方法来同时进行参数估计和异常值检测。在本文中，用Bayesian的思想和原理[9-11]，并引入Gibbs抽样算法[12]，可以把参数估计和异常值检测同时实现。而不是先估计参数，再检测异常值，避免了参数估计和异常值检测相互影响的问题。为了验证该方法的正确性，本文进行了大量的模拟实验，验证了该方法的可行性和有效性。

1基于Bayesian方法的参数估计和异常值检测

多元线性回归模型一般形式为

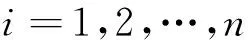
其中，p(给定)为解释变量的数目；βj(j=0,1,…,p)为回归系数；εi～N(0,σ2),i.i.d.i=1,2,…,n；β=(β0,β1,…,βp)T；σ2为未知参数。

对每个观测值，引入异常值识别变量

记δi为第i个异常程度的大小。并且假设：每个观测值受到异常扰动的先验概率都为α，即p(δi=1)=α。

1)根据共轭先验分布的选取准则和实际应用需要，取参数的先验分布分别为

其中，μ，ξ，α，β*，V，ν和λ为超参数。

根据以上假设，加入了异常值的多元线性模型为均值转移模型(mean-shift)。

为判定观测值中是否含有异常值以及确定它们的阈值，构造如下Bayesian假设检验问题。

根据Bayesian假设检验的原理，当H1对应的后验概率p(γi=1|Y)，Y=(y1,y2,…,yn)T大于H0对应的后验概率p(γi=0|Y)即p(γi=1|Y)>0.5时，认为H1成立，从而认为第i个观测值为异常值；否则，认为第i个观测值为正常值。这样，问题就归结为计算每个观测值为异常值的后验概率p(γi=1|Y)。

2基于Gibbs抽样的后验概率值的计算和参数的估计

2.1参数的全条件分布

由于后验概率p(γi=1|Y)涉及的分布比较复杂，下面引入Gibbs抽样算法来解决这些后验概率值的计算问题。为此，根据Bayesian定理可得下列全条件分布。

Y的联合概率密度函数为

(1)

(1)式中：β=(β0,β1,…,βp)T；δ=(δ1,δ2,…,δn)T；γ=(γ1,γ2,…,γn)T。

1)由Bayesian定理，在Y,σ2,δ,γ给定时，β的全条件分布为

(2)

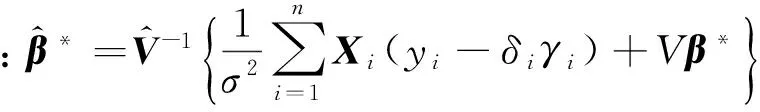
这里Xi=(1,x1i,…,xpi)T。

2)在Y,β,δ,γ给定时，σ2的全条件分布为

(3)

(3)式中：v1=n+v，

3)在Y,β,σ2,δ,γ(-j)给定时，γj的全条件分布为

(4)

(4)式中：

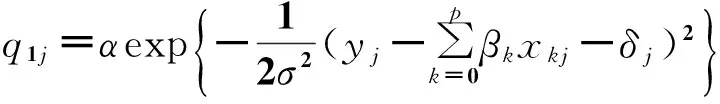
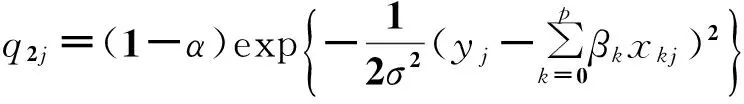
4)在Y,β,σ2,δ(-j),γ给定时，δj的全条件分布为

(5)

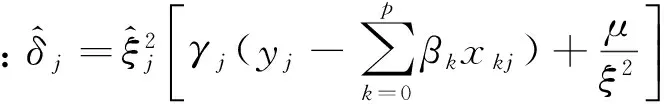
2.2识别变量后验概率值的计算

设β(r),(σ2)(r),δ(r),γ(r)，r=1,2,…,R为用Gibbs抽样算法从上述全条件分布中抽取的样本，则异常值的识别变量后验概率值的公式为

(6)

2.3参数β的估计

同理，参数β的估计值为

(7)

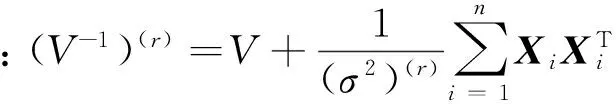
3线性模型异常值检测的Bayesian方法的实施具体步骤

第1步确定先验分布中的超参数。例在本文中给出这些超参数的一组具体取值如下

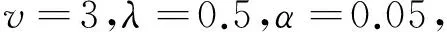
第2步由Bayesian估计方法和超参数的取值，确定Gibbs抽样的初值。

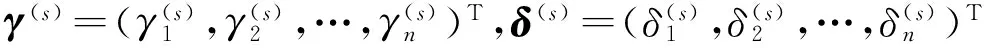
向量的上角标(i,k)的含义为：该向量的第1个分量到第k-1个分量是第i+1次抽样的样本，第k个分量到最后一个分量为第i次抽样抽取的样本。例：(γ)(s-1,j)=((γ1)(s),…(γj-1)(s),(γj)(s-1),…,(γn)(s-1))T。

重复上述抽样过程直到Markov链达到稳定，取稳定之后的R个Gibbs样本

第4步按照(1)—(3)式计算识别变量的后验概率值，并按判定规则对异常值判定。

第5步按照(4)式估计参数β的大小。

4算例与分析

4.1算例

从三元正态分布β～N(β*,V-1)中随机抽取一个向量为(-0.018,2.029,-1.028)T。

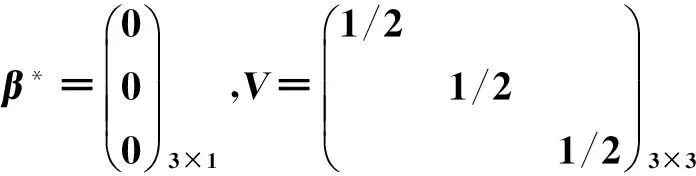
将上述向量只取整数为(0,2,-1)T。

故考虑模型

经模拟产生100个数据。其中，(x1i,x2i)T，i=1,2,…,100来自于二元标准正态分布。

下面用3种方案进行模拟和实验。

方案1在第19个观测值上加上一个大小为-5的异常扰动。

方案2在第20和79个观测值上分别加上大小为的2.5，-4的异常扰动。

方案3在第19至23个观测值上分别加上大小为-6，4，9，-7，8的异常扰动。

4.2异常值检测

用Bayesian方法异常值识别变量的后验概率值如图1所示。由图1a可以看出，第19个观测值为异常值的后验概率大于0.5，判定为异常值；由图1b可以看出，第20个和第79个观测值为异常值；由图1c看出，从第19到23个观测值均被检测出为异常值。

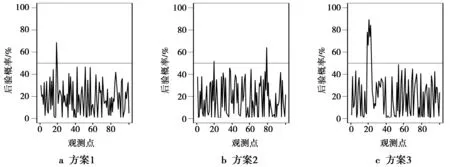
图1　基于方案1-3的识别变量后验概率值Fig.1　Posterior probabilities of these classification variables based on the schemes of 1-3

下面分别用3种稳健的估计方法：LTS估计、M-估计和S-估计先估计参数，再进行异常值判断(用3sigma准则)。对方案1，3种方法与Bayesian估计同样都能检测出第19个观测值为异常值。对方案2，3种方法都能检测出第79个观测值为异常值，但是无法检测出第20个观测值为异常值。由此说明，Bayesian方法对异常值更加敏感。对方案3，由于遮蔽现象，3种方法都能检测出第19，21，22，23个观测值为异常值，但都无法检测出第20个观测值为异常值。说明Bayesian对异常值的遮蔽现象有一定作用，能有效地检测出连续几个在一起的异常值。

4.3参数估计

模型中参数β的真实值为(0,2,-1)T。3种方案参数估计的结果分别对应于表1-3。从3个表中的数据可以看出，Bayesian方法估计出的参数值准确度相对较高。

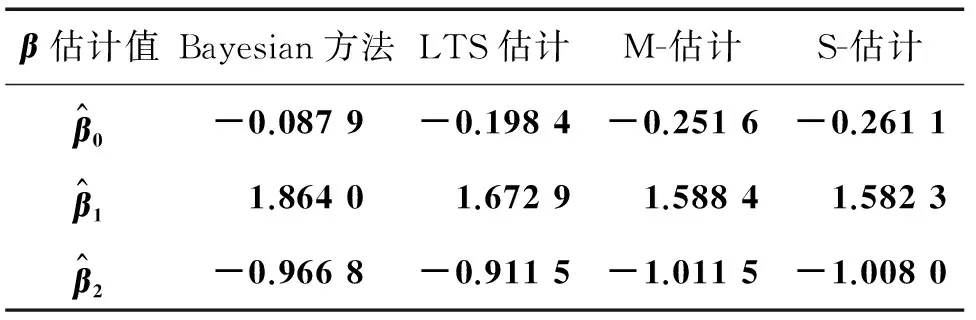
表1　基于方案1的4种方法的参数估计值

故用Bayesian方法来同时进行参数估计和异常值检测是行之有效的。

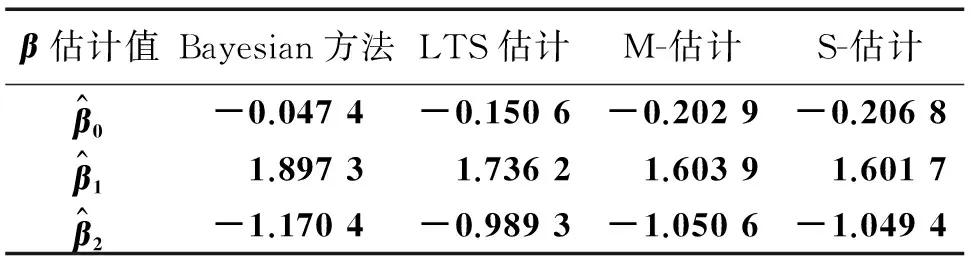
表2　基于方案2的4种方法的参数估计值

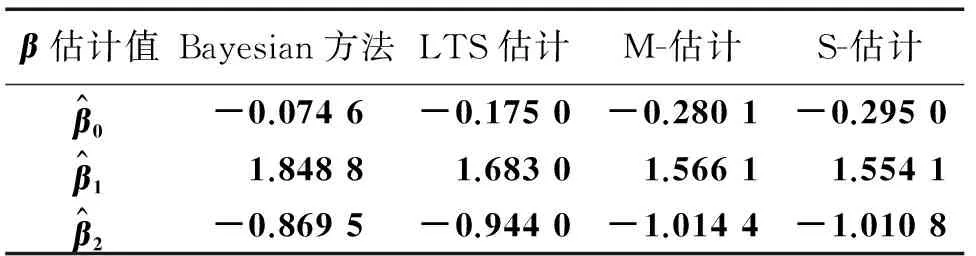
表3　基于方案3的4种方法的参数估计值

5结束语

异常值检测是当前数据分析研究中的一个热点问题。本文是在线性模型的基础上，引入识别变量，基于Bayesian方法并结合Gibbs抽样算法，给出识别变量的后验概率值的计算方法和参数的估算方法；同时估计模型参数和进行异常值检测。进行了大量的模拟实验，结果表明，该方法对于解决线性模型数据中异常值检测和参数估计是可行和有效的。

参考文献：

[1]HAMPEL F R, RONCHETTI E M, ROUSSEEUW P J, et al. The Approach based on Influence Functions.[M]New York: John Wiley and Sons, 1986.

[2]HUBERT M, ROUSSEEUW P, VAN A S. High-breakdown robust multivariate methods[J]. Statistical science, 2008,23(1),92-119.

[3]MCCANN L, WELSCH R E. Robust Variable Selection Using Least Angle Regression and Elemental Set Sampling[J].Computational Statistics & Data Analysis, 2007, 52(1),249-257.

[4]ROUSSEEUW P J, VAN D K. Computing LTS regression for large data sets [J]. Data Mining and Knowledge Discovery, 2006,(12),29-45.

[5]HUBER P J.Robust Statistics[M].New York:Wiley,1981.

[6]DAVIES P L. Asymptotic behavior of S-estimates of multivariate location parameters and dispersion matrices[J]. Ann, Statist, 1987,(15),1269-1292.

[7]MARONNA R A, MARTIN D R, YOHAI V J. Robust Statistics:Theory and Methods,Chichester[M]: New York:Wiley, 2006.

[8]SHE Y, OWEN A B. Outlier detection using nonconver

penalized regression[J].Journal of the American Statistical Association, 2011,106(494),626-639.

[9]BERGER J O. Statistical decision theory and Bayesian analysis[M]. New York:Wiley,1985.

[10] 茆诗松．贝叶斯统计学[M].北京：中国统计出版社，1999.

MAO Shisong. Bayesian statistics[M]. Beijing: Statistics Press of China, 1999.

[11] 吴喜之.现代贝叶斯统计学[M].北京：中国统计出版社，2000.

WU Xizhi, Modern Bayesian statistics [M]. Beijing: Statistics Press of China, 2000.

[12] CHRISTIAN P R. Monte carlo statistical methods [M]. Berlin:Springer, 2004.

Parameter estimation and outliers detection based on Bayesian method

SHANG Hua1, FENG Mu2, ZHANG Beibei1

(1. College of Statistics, Capital University of Economics and Business, Beijing, 100070, P.R. China;2. College of Management, University of Science and Technology of China, Hefei, 230000, P.R. China)

Abstract:Outliers detection is an important research field in the current data analysis. Outliers in the data will affect the modeling, estimating parameters, forecasting and other issues directly. The conventional methods of outliers detection based on the model are to estimate the model parameters firstly, and then detect the abnormal value. The presence of outliers affects the parameter estimation, which results the in unreliability of outlier detection consequently; On the contrary, the presence of outliers will affect the parameter estimation. In this paper, we propose a new outliers detecting method based on Bayesian method, which can estimate parameters and detect outliers simultaneously. This method is introducing classification variables into linear regression model. Using Gibbs sampling a procedure for computing the posterior probabilities of classification variables and obtaining the estimation of parameters is designed. The outliers can be detected by comparing the posterior probabilities of these classification variables. A large number of simulation experiments illustrate that the proposed method is more sensitive to outliers compared with traditional methods.

Keywords：linear regression; classification variables；parameter estimation; outlier; Bayesian method; Gibbs sampling

DOI：10.3979/j.issn.1673-825X.2016.01.021

收稿日期：2015-03-12

修订日期：2015-10-12通讯作者：尚华hnshanghua@tom.com

基金项目：国家自然科学基金(11426159)；首都经济贸易大学研究生科技创新项目(12013120061)

Foundation Items：The National Natural Science Foundation of China(11426159); The Postgraduate Technology Innovation Project of Capital University of Economics and Business (12013120061)

中图分类号：TP391

文献标志码：A

文章编号：1673-825X(2016)01-0138-05

作者简介：

尚华(1981-)，女，河南新乡人，讲师，在读博士，研究方向为数理统计，数据挖掘。E-mail:hnshanghua@tom.com。

冯牧(1989-)，女，湖南岳阳人，在读博士，研究方向为时间序列，数据挖掘。

张贝贝(1983-)，女，河南济源人，讲师，博士，研究方向为时间序列，数据挖掘。

(编辑：张诚)