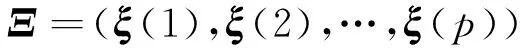基于先验知识的广义旁瓣对消器STAP

唐　斌，吴宏刚，陈客松，杨晓波

(1.电子科技大学 电子工程学院，成都 611731; 2. 中国民用航空总局第二研究所，成都 610041;3. 成都航空职业技术学院 航空电子工程系，成都 610100)



基于先验知识的广义旁瓣对消器STAP

唐斌1,3，吴宏刚2，陈客松1，杨晓波1

(1.电子科技大学 电子工程学院，成都 611731; 2. 中国民用航空总局第二研究所，成都 610041;3. 成都航空职业技术学院 航空电子工程系，成都 610100)

摘要：空时自适应处理(space-time adaptive processing，STAP)算法的运算量与处理性能构成了一对矛盾。利用广义旁瓣对消器(generalized sidelobe canceller，GSC)形式的处理器结构，提出一种基于先验知识的 STAP算法以解决该问题。该算法使用相控阵雷达系统参数以及阵列几何模型等先验知识来构建空时杂波的匹配矩阵，并计算空时多约束导引矢量，实现对STAP算法的自适应加权初始化。该算法的优点是无需协方差矩阵求逆从而使处理速度得到加快。仿真实验表明该算法的处理性能未受影响，而收敛速度则明显提高。

关键词：空时自适应处理；先验知识；协方差矩阵；广义旁瓣对消器

0引言

由于载机相对地面飞行，造成机载相控阵雷达的目标回波信号可能完全被地杂波所淹没，使得地面动目标检测非常困难。空时自适应处理(space-time adaptive processing，STAP)对于在强杂波环境中检测微弱目标较为有效[1-2]，STAP全维处理器的性能是最优的，但运算量也最高，以现有的DSP(digital signal processor),FPGA(field programmable gate array)等技术水平，仍难以解决空时全维处理运算的实时性问题[1-3]。特别是当阵元数和脉冲数较多的情形下，这种矛盾更加突出。在工程上，尤其是在战争环境中，实时性差的算法几乎没有实用价值。

改善空时自适应信号处理算法的目的主要有2个：①在一定的约束条件下提高算法的处理性能，②降低所需的样本支持以及降低算法的总运算量。近几年提出了大批降秩、降维算法[3-7]。这些算法多数是通过降低少量性能来换取实时性的提高。STAP的运算量与处理性能成了矛盾的2个方面。本文就降低运算量并提高处理性能进行了探索，发现大量运算可搬移到离线处理中，用离线方式进行预处理，剩余的少量运算由在线处理来完成。

1相控阵雷达的杂波环境先验知识

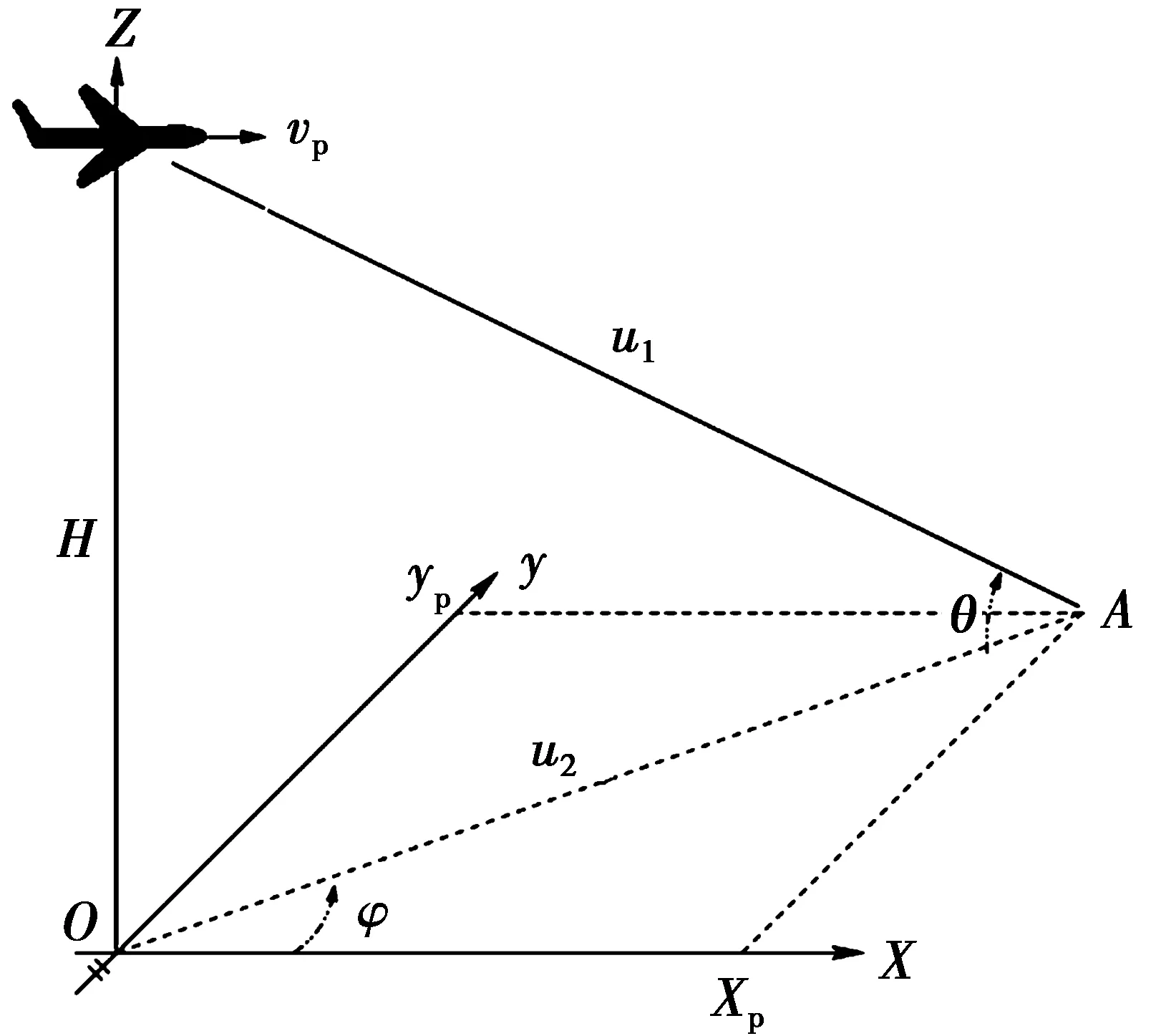
图1　机载相控阵雷达阵列几何Fig.1　Platform geometry of airborne phased array radar

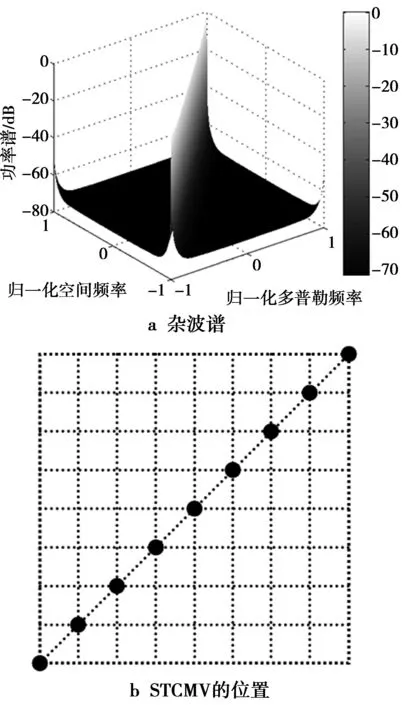
机载正侧视阵的空时二维杂波谱及其俯视图见图2。图2中归一化空间频率表示锥角的余弦，归一化多普勒频率表示2fd/fr(fd表示多普勒频率，fr为脉冲重复频率)。从图2可看出，地面杂波位于空时二维平面的对角带上。如果将杂波投影到任意一维上，则均为宽带信号，基本上占满了整个区间，且有用信号被淹没在杂波之中。如果单用空间波束形成或者时域动目标指示来处理，则均不可能分离出目标信号。根据目标与杂波的二维可分离性，只有做空时二维联合自适应处理，才能在杂波处形成自适应凹陷，从而抑制掉全部杂波，并检测出目标。

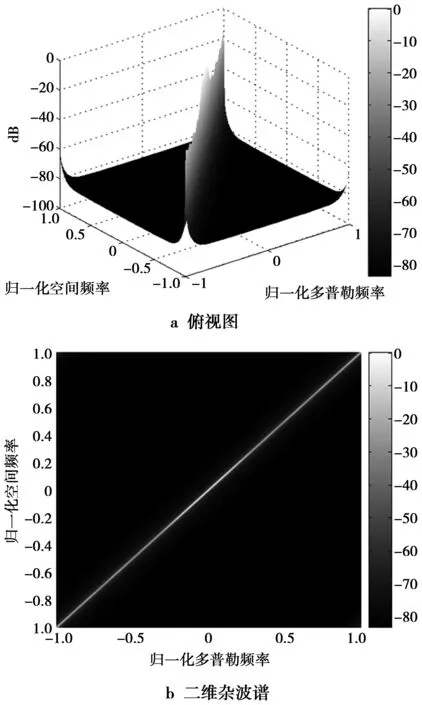
图2　地杂波的空时二维谱Fig.2　Space-time 2D spectrum of ground clutter

(1)

非零特征矢量相互正交。杂波子空间用C(Rq)表示。易知，C1(Rq)⊂C(Rq)。

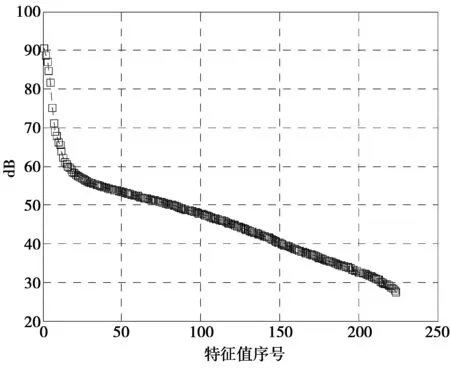
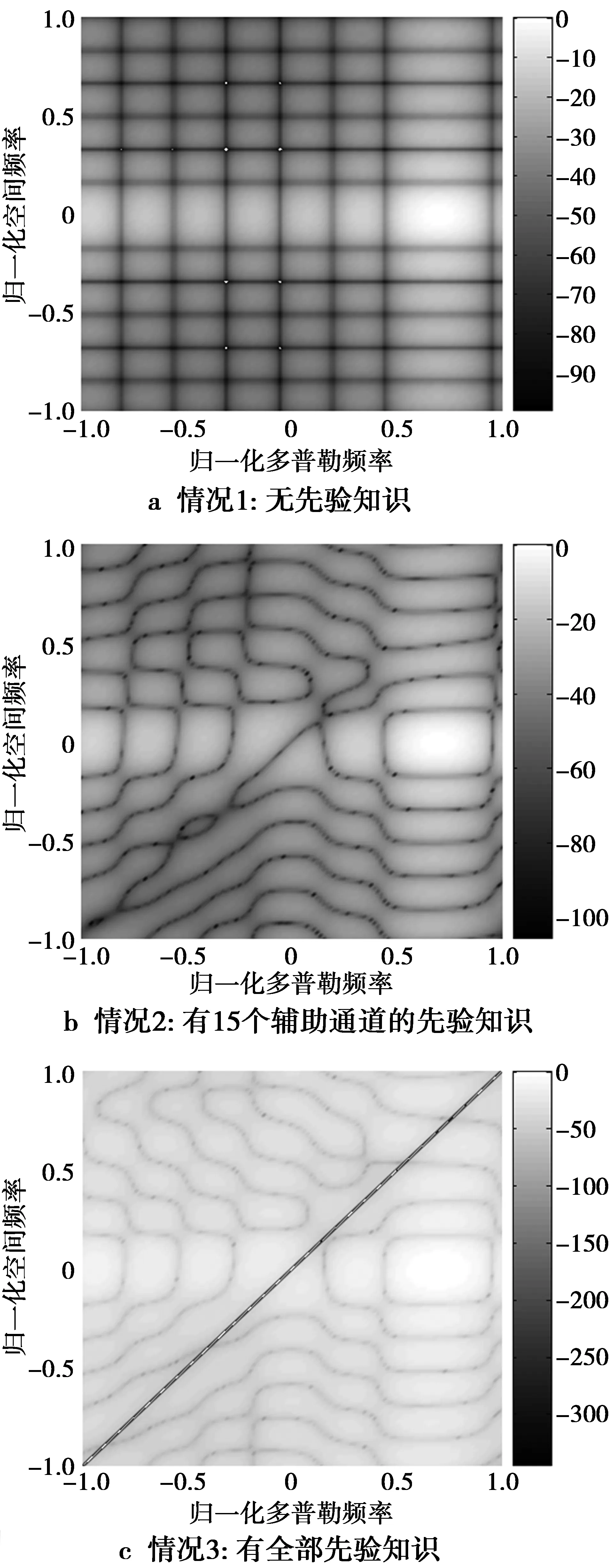
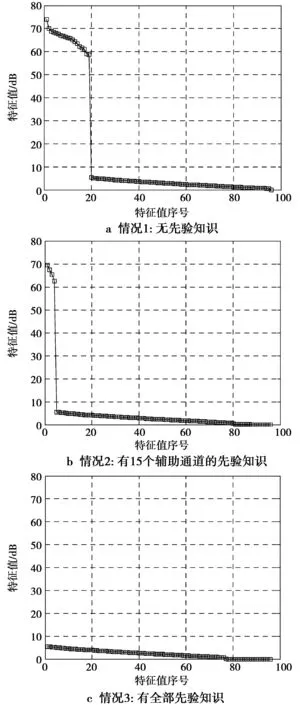
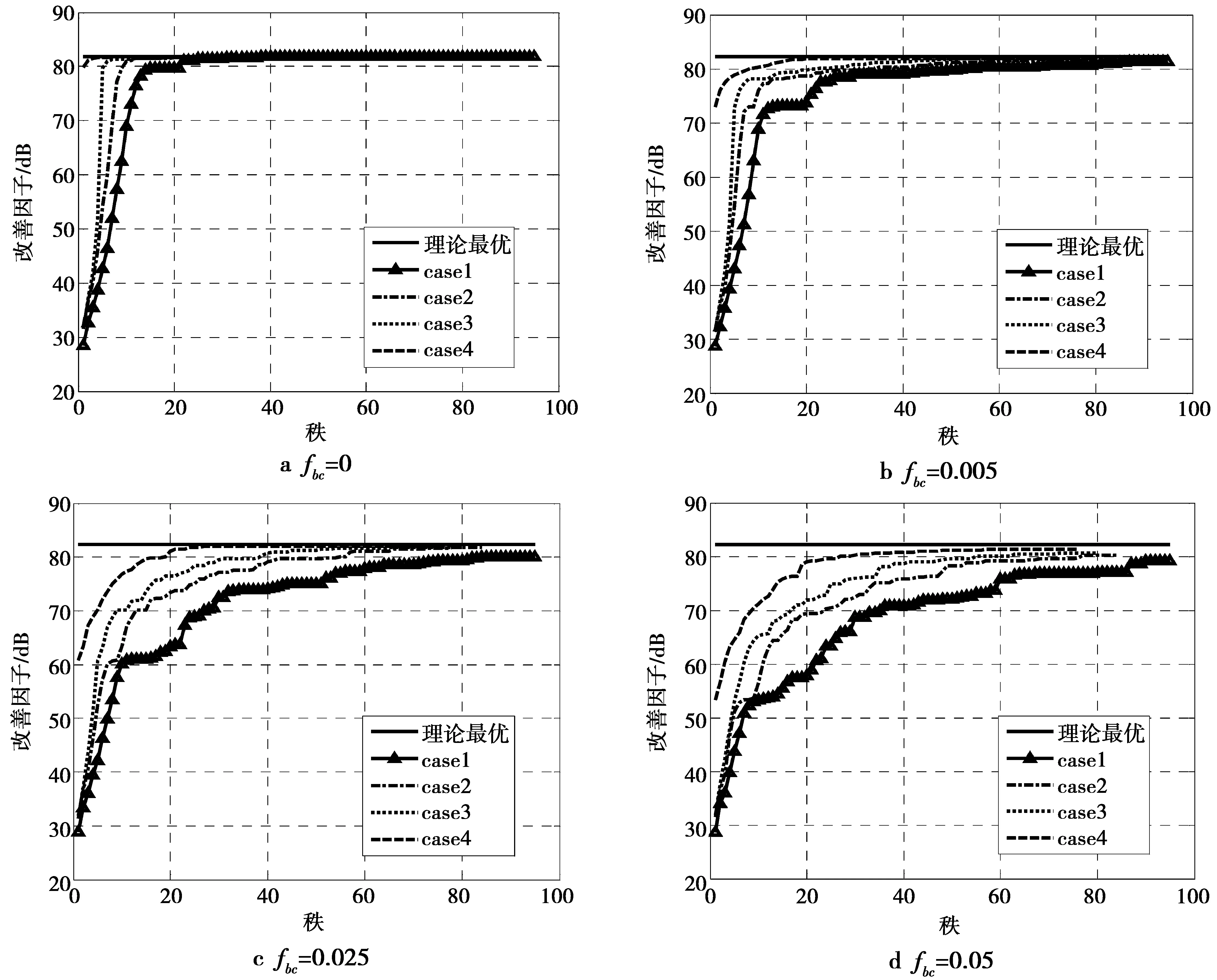
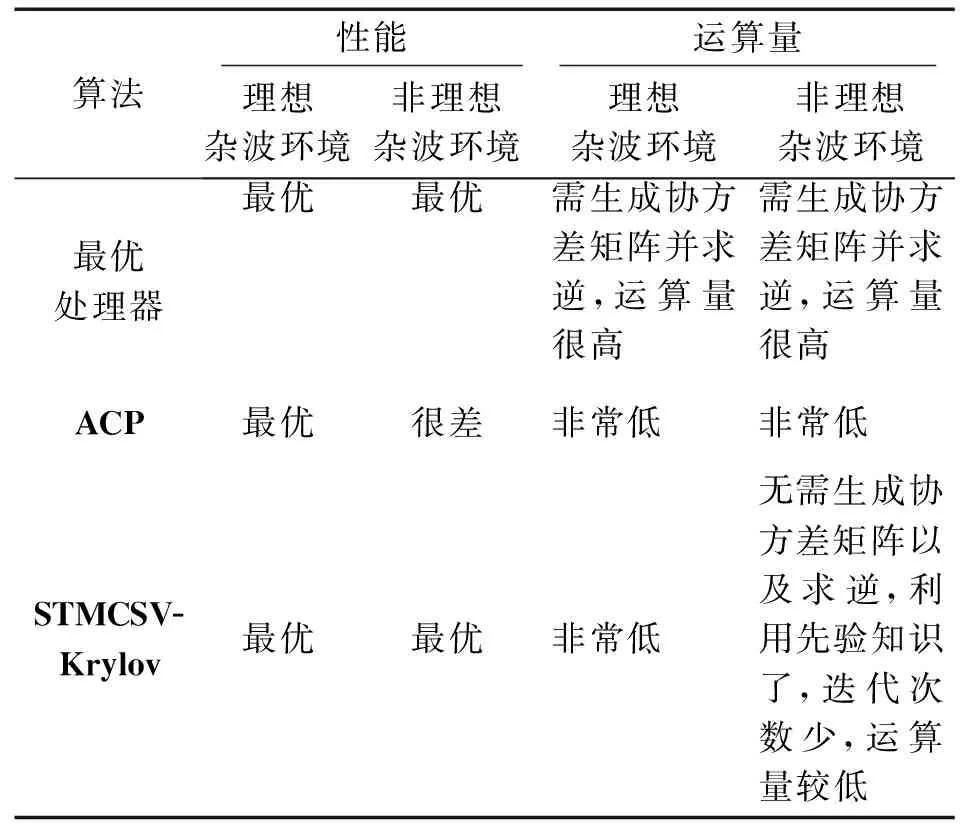
理想杂波子空间维数D≤D0[10-11]。如果阵列天线为有向天线，则D

实际工程中存在各种非理想因素，因此D≤D0的这个结论不成立。因为各种非理想因素对杂波自由度的影响，杂波相关矩阵除了有D个大特征值以外，还有一些小特征值。

非理想情况下，由理想杂波子空间之外的非零特征矢量张成的子空间就称为非理想杂波子空间：

(2)

易知，C2(Rq)⊂C(Rq)。对于正侧视阵，它是前Dκ个大特征值之外的那部分非零特征矢量张成的。通常难以明确界定非理想杂波子空间，因为工程中大小特征值之间没有明显区别。比如美国的Mountaintop实测数据(图3)[12]以及多通道机载雷达测量(multi-channel airborne radar measurements，MCARM)数据[13]的特征谱分布。

图3　Mountaintop实测数据的特征谱Fig.3　Eigenspectrum of the measured Mountaintop data

用正交于杂波子空间C(Rq)的任何矢量作为加权时，均可充分抑制杂波[9]。由此可知，为充分抑制杂波，自适应权矢量一定位于正交于C(Rq)的噪声子空间N(Rq)。但因C(Rq)经常扩展到整个空时域而形成NM维杂波子空间，即C=C(Rq)=C1(Rq)⊕C2(Rq)，所以噪声子空间与杂波子空间有部分重叠，不可能找到只含有噪声的N(Rq)，必须想别的办法来抑制杂波。

Klemm提出的辅助通道法(auxiliary channel processing，ACP)及其改进方法[6,10-11]在理想正侧视线阵下，其性能可达到最优。本质上说，该算法是利用了杂波脊位置、协方差矩阵的大特征值个数这2种先验知识。因为所选的辅助通道对应的空时二维导引矢量所张成的子空间恰好就是杂波子空间，那么，用辅助通道把采样数据变换至波束-多普勒域可获得全部杂波信息。但这属于固定结构降维算法，缺点是难以应对变化的杂波环境，先验知识并不是全部知识。只要有内部杂波运动、阵元幅相误差等非先验的因素影响，ACP的性能就快速下降。有鉴于此，本文提出了基于先验知识的Krylov子空间STAP方法。该方法把波束-多普勒域中先验知识(阵列几何、理想杂波脊、主波束等)作为约束条件，而剩下的非理想杂波子空间里的全部小杂波特征矢量属于非先验知识，就交给在线处理。由于在Krylov子空间中能更有效地用数学表达先验知识且能实现对非先验知识的自适应处理，所以选择在Krylov子空间中进行处理。

因为仅需要相控阵雷达系统、载机飞行几何等知识，而这些知识完全已知，故可离线生成约束条件。

2利用先验知识辅助的STAP方法

2.1降秩Krylov子空间

Krylov子空间降秩自适应方法的基张成了Krylov子空间[14]，样本数据被投影到低维子空间，再在该低维子空间中用低秩空时滤波器进行处理，则计算量得以减少且收敛速度更快。

给定矩阵R和矢量s，定义

(3)

称为与(R,s)对相对应的第D个Krylov子空间，或称为秩D的Krylov子空间，表示为κD(R,s)，其中R为方阵。

κi(R,s)(i=1,2,…,NM)形成了Krylov子空间序列

(4)

(5)

(6)

对Krylov子空间逐步扩张，自适应加权的均方误差就逐步变小。只要均方误差比设定的阈值小，就不再扩张Krylov子空间。多数情况下，STAP不用扩张到秩NM的Krylov子空间κNM(R,s)就可得到所需的空时自适应最优权。设在κD(R,s)中获得最优权，则D可能远远小于NM。在κD(R,s)中求得的最优权与在κNM(R,s)中求得的最优权的均方误差如果很小，这时杂波子空间C(Rq)就近似等效于κD(R,s)。因此，Krylov子空间算法把全秩NM降为部分秩D。NM定义了D的上界[15]。

(7)

选择系数{αi}的准则为最小均方误差或最大化输出信杂噪比。

2.2先验知识

空时杂波匹配矢量(space-timecluttermatchedvector，STCMV)是与空时杂波的空域、时域均相匹配的导引矢量。由于杂波空域位置以及对应所在空域的杂波多普勒频率均为已知，故使用p个STCMV设计NM×p维的空时杂波匹配矩阵

(8)

(8)式中:ξ(i)(i=1,2,…,p)是与杂波方向和多普勒频率匹配的STCMV;p是STCMV的个数。理想情形下，STCMV均匀分布于杂波脊上，p=D0。非理想情况下，要增加辅助通道的个数使之大于D0，目的是减少雷达系统带宽、杂波带宽等造成的时域解相关、空域解相关的影响。令Ω=span(ξ(1),ξ(2),…,ξ(p))，那么正交于杂波子空间C(Rq)的噪声子空间就是Ω的补空间：

Ω⊥=span(ξ(p+1),ξ(p+2),…,ξ(NM))

(9)

有用信号的导引矢量知识是已知的。为把该先验知识利用起来，令

(10)

下面设计空时多约束导引矢量(space-time multi-constraint steering vector，STMCSV)

(11)

图4　选择STCMV的方法Fig.4　Approach of selecting STCMV

3仿真实验

本实验目的是考察先验知识对Krylov子空间中STAP收敛速度的影响。实验采用的STAP处理器结构为广义旁瓣对消器(generalizedsidelobecanceller,GSC)。

3.1理想杂波环境下的实验

在该实验中的上支路设计为用wSTMCSV对采样数据q进行变换，而下支路生成阻塞矩阵B。用直接求零空间法来求得阻塞矩阵B。该矩阵是降维矩阵，阻塞后的数据q0的协方差矩阵的维数为(NM-(N+M-1))×(NM-(N+M-1))。设相控阵雷达有N=12个阵元，M=8个脉冲，杂噪比CNR=60 dB，导引矢量对应的归一化的空间频率为0，归一化的多普勒频率为0.72。理想情形下，不同先验知识所对应的STMCSV的方向图见图5，均为俯视图。图6给出了被阻塞矩阵所阻塞后数据的特征谱。

对比图5和图6，无先验知识情况下，图5a中方向图就是有用信号导引矢量的方向图，图6a中阻塞后杂波仍有19个大特征值，大特征值个数没有降低。

知道15个辅助通道的先验知识的情况下，图5b是在有用信号导引矢量方向图中生成了一小段零陷而构成的方向图，图6b中阻塞后的杂波还剩余4个大特征值，大特征值个数降低了15个。

图5　不同先验知识所对应的STMCSV的方向图Fig.5　Pattern of STMCSV corresponding to differentprior knowledge

知道全部辅助通道的先验知识的情况下，图5c是在有用信号导引矢量方向图中的整条对角线上生成了零陷而得到的，图6c中阻塞后杂波的大特征值全部被去掉，表示杂波成分通过预处理被完全除掉了，大特征值个数为0，阻塞后数据中仅含白噪声。所以，理想情形下的STMCSV已经是一种最优权，此时STMCSV与ACP的权矢量等效。下支路用无需构建协方差矩阵且无需对协方差矩阵求逆的Krylov子空间空时自适应处理。这里把所提出的新方法称为STMCSV-Krylov法。

在理想杂波环境中，本方法与ACP法都直接利用的是理想杂波脊的信息，二者性能相同，但两者结构不同，STMCSV-Krylov法使用的是GSC结构，ACP使用的是直接处理结构处理器。

图6　阻塞后的数据的特征谱Fig.6　Eigenspectrum of the blocked data

3.2非理想杂波环境下的实验

在利用了理想杂波脊的先验知识的前提下，下面仿真杂波相对带宽fbc对改善因子(improvementfactor，IF)的影响。杂波相对带宽fbc是指杂波带宽fc与脉冲重复频率比值[10]。仿真条件除了杂波相对带宽fbc外，其余条件均与图6的仿真条件相同。图7中case1到case4分别对应知道0个、11个、15个、19个STCMV的情况。图7中横坐标表示Krylov子空间的秩。若知道一定的先验知识，就能使算法的迭代次数减少。比如，图7中case1对应完全不知道任何先验知识的情况，需要迭代的次数为20多次才能达到最佳改善因子，而要达到相同的改善因子，case3不到10次即可实现，从而运算量得以减少。从图7可以看出，case1到case4所对应的4条曲线之间的相对关系不随杂波相对带宽大小而变化，都呈总体上升趋势。如果杂波相对带宽变大，则曲线总体上升变慢。这是由于杂波相对带宽变大后，其特征值扩展到理想杂波子空间之外的非理想杂波子空间，使得非理想杂波子空间维数变高。随着杂波相对带宽增大，杂波脊逐渐展宽，原有的先验知识占总的杂波知识的比重就越小，从而收敛所需迭代次数就越高。

由于ACP法中没有迭代自适应处理，故仅仅利用了理想杂波脊先验知识的ACP法的性能对应的是case4的曲线的起点处的性能。从图7a-图7d中的case4可以看出，随着fbc从0增加到0.05，case4改善因子的起点从80dB，74dB，61dB一直下降到54dB。也就是说，面对杂波相对带宽展宽这种情况时，ACP法的性能急剧下降。杂波越是非理想，则ACP法的性能下降越快。

图7　不同fbc的情况下IF的变化Fig.7　Change of IF in the cases with different fbc

在非理想杂波环境中，比如杂波相对带宽展宽的情况下，STMCSV-Krylov法与ACP法均利用了理想杂波脊的先验知识，但由于是非理想杂波环境，2种算法都不知道杂波脊的全部信息。ACP法仅利用理想杂波脊这种部分知识来生成最终权矢量，就无法抑制大量的非理想杂波脊成分，造成ACP法在面对非理想杂波环境时，性能急剧下降。而STMCSV-Krylov法首先利用了理想杂波脊的知识，然后采用迭代自适应处理来生成最终的最优权矢量，其性能与最优处理器相同，但因为利用了先验知识，故运算量得以下降。

实际战场环境中，除了杂波带宽展宽外，还有阵元幅相误差、载机偏航等多种非理想因素。工程上，首要考虑的是算法的性能，其次才是运算量。ACP法没有自适应处理环节，因此运算量比STMCSV-Krylov小。但因为ACP法只能处理理想杂波环境，其应对非理想杂波环境时的性能不足，所以在实际战场杂波环境中没有实用价值。表1给出了最优处理器、ACP，STMCSV-Krylov在理想及非理想杂波环境下的性能和运算量的比较。

4结论

为了提高STAP的运算效率并维持或增强算法性能，提出了基于先验知识的STMCSV-Krylov法。仿真结果表明新方法能利用先验知识有效地进行杂波抑制。足够的先验知识能大幅度提高新算法的收敛速度。该方法无需对样本协方差矩阵进行求逆，因而节省了计算量且使系统框架得到简化。总之，新算法把自适应降秩与固定结构降维的优点结合起来，得到了空时自适应处理最优权，且运算速度也得以提高。

表1　算法比较

参考文献：

[1]FERTIG L B. Analytical expressions for space-time adaptive processing(STAP) performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1):442-453.

[2]EL Khatib A, ASSALEH K, MIR H. Space-time adaptive processing using pattern classification[J]. IEEE Transactions on Signal Processing, 2015, 63(3): 766-779.

[3]TANG Bo, ZHANG Yu, TANG Jun. Robust fast maximum likelihood with assumed clutter covariance algorithm for adaptive clutter suppression[J]. IET Radar, Sonar & Navigation, 2014, 8(9): 1184-1194.

[4]张永顺, 冯为可, 赵杰, 等．时变加权的机载双基雷达降维空时自适应处理[J]. 电波科学学报, 2015, 30(1):194-200.

ZHANG Yongshun, FENG Weike, ZHAO Jie, et al. A dimension-reduced STAP method for airborne bistatic radar based on time-varying weighting techniques[J]. Chinese Journal of Radio Science, 2015, 30(1): 194-200.

[5]WANG Pu, WANG Zhe, LI Hongbin, et al. Knowledge-aided parametric adaptive matched filter with automatic combining for covariance estimation[J]. IEEE Transactions on Signal Processing, 2014, 62(18):4713-4722.

[6]KLEMM R, WARD J. STAP I-architectures and algorithms[C]//IEEE Radar Conference. Rome, Italy: IEEE Press, 2008:1-2.

[7]KANG Bosung, MONGA V, RANGASWAMY M. Rank-constrained maximum likelihood estimation of structured covariance matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 501-515.

[8]MELVIN W L.A STAP overview[J].IEEE Aerospace and Electronic Systems Magazine,2004,19(1),Part:2:19-35.

[9]姜磊, 王彤. 机载非正侧阵雷达自适应子空间方法[J]. 电子与信息学报, 2014, 36(9):2214-2219.JIANG Lei, WANG Tong. A adaptive subspace method for non-side-looking airborne radar[J]. Journal of Electronics & Information Technology, 2014, 36(9): 2214-2219.

[10] KLEMM R. Principles of space-time adaptive processing[M]. London, U.K.: IEE Press, 2006.

[11] KLEMM R. Applications of space-time adaptive processing [M]. London, U.K.: IEE Press, 2004.

[12] TITI G W, MARSHALL D F. The ARPA/NAVY Mountaintop Program: adaptive signal processing for airborne early warning radar[C]//International Conference on Acoustics, Speech and Signal Processing. Atlanta, Georgia: IEEE Press, 1996, 2:1165-1168.

[13] BERTACCA M. Long memory models for the analysis and simulation of multi-channel airborne radar measurement (MCARM) data[C]//IEEE Radar Conference. Rome, Italy: IEEE Press, 2008:1-6.

[14] SOMASUNDARAM S D, PARSONS N H, LI Peng, DE LAMARE R C. Reduced-dimension robust capon beamforming using Krylov-subspace techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 270-289.

[15] TANG Bin, WANG Xuegang, ZHANG Chaoshen, et al. Krylov subspace method based on data preprocessing technology[J]. Journal of Systems Engineering and Electronics, 2008, 19(6): 1063-1069.

GSC STAP based on a prior knowledge

TANG Bin1,3，WU Honggang2，CHEN Kesong1，YANG Xiaobo1

(1.School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, P. R. China;2. The Second Research Inst. of CAAC, Chengdu 610041, P. R. China;3. Department of Electronic Engineering, Chengdu Aeronautic Polytechnic, Chengdu 610100, P. R. China)

Abstract:The computational burden and performance of space-time adaptive processing(STAP) have formed a realistic contradiction. A new STAP approach based on a prior knowledge using the generalized sidelobe canceller(GSC) was present to solve the above problem. The new approach employed a prior knowledge of the parameters of phased array radar system and geometry model in order to construct space-time clutter matched vector and matrix. Then space-time multiple-constraint steering vector was computed to initialize the adaptive weight vector of STAP. The novel STAP avoided the covariance matrix inverse in order to obtain fast speed. Finally，the simulated results showed that the method can greatly speed up the convergence with no reduction of performance.

Keywords：space-time adaptive processing; a prior knowledge; covariance matrix; generalized sidelobe canceller

DOI：10.3979/j.issn.1673-825X.2016.01.003

收稿日期：2015-04-01

修订日期：2015-09-28通讯作者：唐斌tbuestc@163.com

基金项目：国家自然科学基金(U1433129)；中国博士后科学基金面上资助项目(2012M511919)；四川省教育厅重点资助项目(14ZA0307, 13ZA0050)

Foundation Items：The National Natural Science Foundation of China (U1433129); The China Postdoctoral Science Foundation (2012M511919); The Scientific Research Fund of Sichuan Provincial Education Department (14ZA0307, 13ZA0050).

中图分类号：TN957

文献标志码：A

文章编号：1673-825X(2016)01-0017-07

作者简介：

唐斌(1974-)，男，四川省广安市人，副教授，在站博士后，主要研究领域为阵列信号处理、自适应信号处理。E-mail: tbuestc@163.com。

吴宏刚(1977-)，男，四川省乐山市人，高级工程师，工学博士，主要研究领域为红外图像处理、民航空管技术。E-mail: comwhg028@sohu.com。

陈客松(1973-)，男，四川省广安市人，副教授，工学博士。主要研究领域为稀疏阵列天线。E-mail: cks149@126.com。

杨晓波(1964-)，男，四川省巴中市人，教授，电路与系统学科博士生导师，主要研究领域为信息探测与对抗。E-mail: xiaoboyang@uestc.edu.cn。

(编辑：魏琴芳)