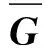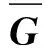显著边缘直接引导的动态模糊图像盲复原方法

付　强，孙秀霞，刘树光，徐　嵩，彭　轲

(1. 空军工程大学 航空航天工程学院，陕西 西安 710038； 2. 95910部队，甘肃 酒泉 735018)



显著边缘直接引导的动态模糊图像盲复原方法

付强1，孙秀霞1，刘树光1，徐嵩2，彭轲1

(1. 空军工程大学 航空航天工程学院，陕西 西安 710038； 2. 95910部队，甘肃 酒泉 735018)

摘要：针对主动视觉中运动载体和云台抖动导致图像模糊的问题，提出一种显著边缘直接引导的动态模糊图像盲复原方法。为了克服经典Canny算子只能对边缘进行标注的缺陷，设计了图像边缘搜索-增强算法，并基于此提出了仅依据图像中显著边缘邻域完成点扩散函数优化估计的方法；为解决传统残差图像方法不能适应预测图像错位的问题，提出图像解模糊的递归残差修正算法来抑制复原图像波动；设计了图像复原的分层迭代处理流程，保证模糊图像复原的可靠性和精度。理想光照条件下的仿真表明，算法能准确恢复模糊图像的边缘，同时抑制复原图像中的波动。非理想光照条件下的仿真也验证了算法对环境有良好的适应性,具有较高的实际应用价值。

关键词：盲复原；显著边缘；点扩散函数(PSF)；递归残差；分层迭代

0引言

图像动态模糊的生成模型即点扩散函数(point spread function，PSF)不同于摄像机失焦模糊，无法依据摄像机固有光学特性直接构建。PSF与曝光周期内的运动直接相关，且该运动难以被直接测量，即使通过与摄像机固连的惯性测量单元(inertial measurement unit，IMU)也难以被准确测量，并且在时间上也难以与摄像机的曝光周期同步。

目前在国内外针对模糊图像处理的研究文献中，其算法大多依赖PSF，需要较大的计算量，耗费大量时间，并且当主动视觉工作在高动态环境下时对图像处理的实时性要求更高。文献[1-2]提出了由多幅图像去模糊模型，而仅对单幅图像的处理显然更困难。经典的图像复原算法有逆滤波、维纳滤波以及基于贝叶斯分析图像的复原算法等，比如利用维纳滤波复原图像，该方法的关键是已知成像系统的传递函数和噪声的统计特性，以一种并非最适合人眼的方式对图像进行了平滑[3]；基于贝叶斯理论的迭代复原算法复原效果好，但耗时长[4]；Lucy-Richardson(LR)算法作为图像复原的经典算法之一，在进行图像复原时，对退化过程的先验知识要求较少且复原效果比较好[5]。但是通常情况下，我们并不关心整幅图像的清晰程度，而是所需信息是否满足后续处理的需求。针对这种情况，我们只需恢复出所需要利用的有效信息，并不是把模糊图像完全恢复清晰，这样一方面大大减少计算量，一方面增强算法适用的针对性。

在视觉量测中，所获得图像往往具备包含显著边缘这一特点，因此，该方法可抑制动态模糊对视觉量测的影响，同时也可仅针对视觉测量感兴趣的显著边缘进行图像复原，从而进一步提高算法效率。本文根据动态模糊对图像中显著边缘的影响在整个图像中占据主导地位这一特性，提出了一种显著边缘直接引导的动态模糊图像盲复原方法。方法由3部分组成：①PSF估计算法的设计；②图像解模糊递归残差修正算法的设计；③图像复原的分层迭代处理流程的设计。该方法针对图像显著边缘及其邻域进行PSF估计和图像解模糊处理，缩小了用于PSF估计的图像范围，提高了估计效率。分层迭代的图像复原算法不但能抑制复原图像中的波动，而且能实现与原清晰图像在图像位置上的精确匹配。

1图像的动态模糊模型

为了更好地分析动态模糊图像的成因，首先对其模型进行建立。一般地，二维图像的动态模糊模型可写成[6]

gb(u,v)=

(1)

(1)式中：u∈[ulb,uub]，v∈[vlb,vub]，其中，[ulb,uub],[vlb,vub]表示二维模糊图像的边界；gc和gb分别表示二维的清晰和模糊图像；h表示二维PSF函数；符号“⊗”表示卷积；符号“=:”表示定义为。

二维图像的离散动态模糊模型为

(2)

(2)式中：u∈[1,nh]∩N；v∈[1,nw]∩N；ru∈N；rv∈N；H(·)为PSF函数；Gc(·)为清晰图像。由于卷积区间有限，由二维连续傅里叶变换和离散快速傅里叶变换(fast fourier transformation，FFT)可知，存在高频信息丢失的问题。因此，即使预知PSF也无法对模糊图像进行完全复原。当h或H未知时(即盲解模糊)，问题的求解更加困难。因此,对于盲解模糊，须根据实际需求有针对性地设计算法。

本文构建针对Gb子区域ΨGb,Sub(Gb,Sub尺寸为nb,Sub×1)的变换以适应本节解模糊算法的设计，ΨGb,Sub的像素数为nb,Sub，并构建一个像素位置对应表LPS(尺寸为2×nb,Sub)。

(3)

2动态模糊图像盲复原方法设计

首先，根据显著边缘的动态模糊特性，设计显著边缘的搜索与增强算法，再由增强后的边缘和与边缘邻域相对应的模糊图像在全图一致性的动态模糊假设下求解PSF，在提高运算效率的同时削弱了边缘模糊邻域外的图像对估计的影响。其次，提出了图像解模糊的递归残差修正算法，在预测图像和点扩散函数均无法准确已知的情况下，能有效抑制显著边缘所引起的复原图像中的波动。最后，设计图像复原的分层迭代处理流程保证了模糊图像复原的可靠性和精度。

2.1利用显著边缘增强的点扩散函数估计方法

一般地，根据清晰边界才能完成视觉量测，阶跃式边缘是被视觉量测所利用的显著特征。在图像复原中，若要有效利用模糊图像的显著边缘，则须解决以下几个问题：①搜索显著边缘；②增强显著边缘；③估计PSF(H)。

2.1.1显著边缘的搜索与筛选

图像显著边缘的搜索是本文实现图像复原的基础。当降低图像分辨率后，则显著边缘在被保留的同时其局部边缘特性变得更为明显，从而可采用现有边缘提取算法提取显著边缘。在现有边缘提取方法中，Canny算子能符合该需求。对于边缘搜索而言，最重要的是对邻接边缘点的搜索，如图1所示，主要包括2种方法：①优先考虑最近距离后考虑最小转向的方法；②优先考虑最小转向后考虑最近距离的方法。方法②可避免方法①出现的“锯齿”，但导致部分边缘点未纳入边缘集合SEd。但只需在方法②中设计相应的像素占用标记算法，以防止搜索出重复的边，如图1中的虚线所示。

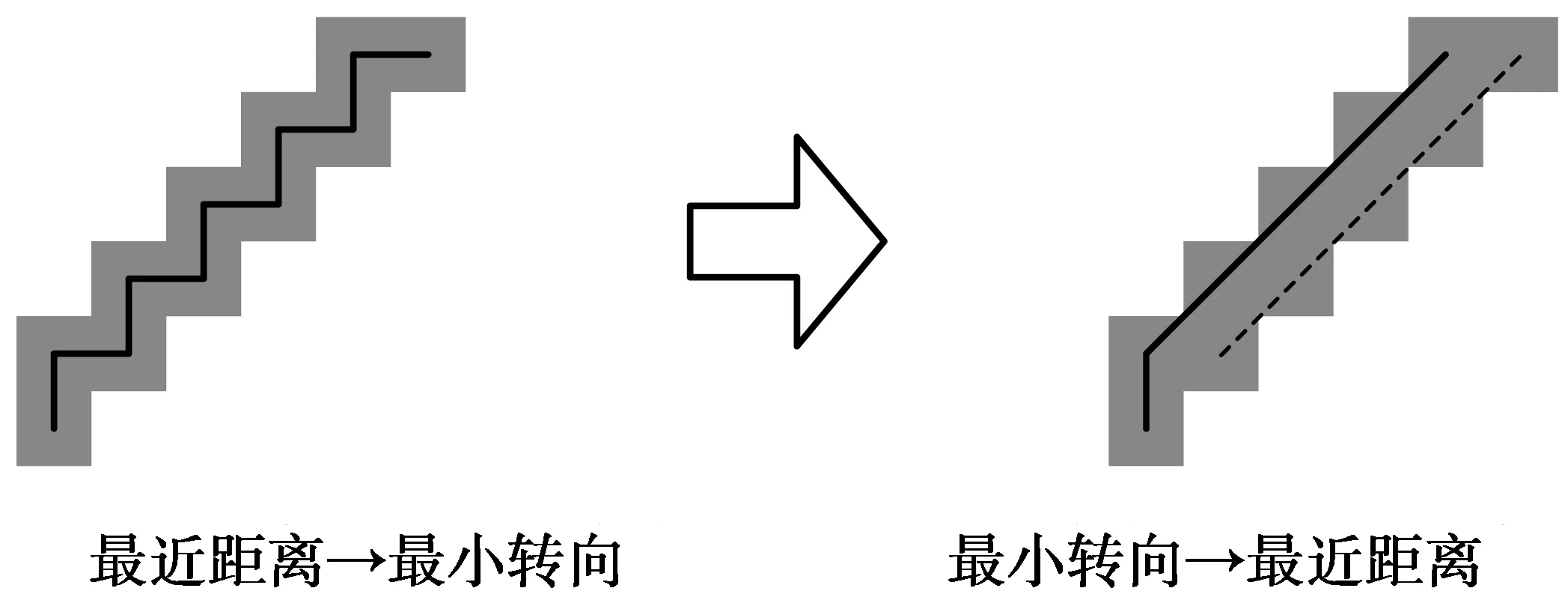
图1　2种不同的边缘搜索算法

然而，Canny算子并不能直接检测出“显著边缘”，必须设计筛选算法才能得到有效的边缘。对边缘集合SEd中转折过大的部分进行分段，并取较长的段作为“显著边缘”。将完成所有边缘1≤iEd≤nEd的搜索与筛选的算法简记为

[LEdV,sCut]=SearchAndPickupEdges

(4)

(4)式中：LEdV为所有有效边缘点的顺序存储；GCur为当前处理图像；lSec和ηTrs分别为筛选边缘时的每个分段的最小长度和转角余弦阈值；wd为转角估计的单边宽度。

2.1.2显著边缘的增强

求解PSF时需要已知或预先估计这部分对应的清晰图像，这里只能采用估计方法，即对显著边缘进行增强处理，并将处理结果作为对应清晰图像的估计值。2.1.1节中得到的边缘集合虽能顺序得到各条边缘上的点，但这些图像位置信息仅仅是像素级的，而边缘增强处理需要指定子像素级的边缘。这里通过曲线拟合与曲面插值相交替迭代的方法完成估计。

ΨEdgeGrad=ExtractEdgePntsAndGrad

(5)

对于离散图像而言，必须将每一点pEdCtr(k)处的梯度矢量离散化。将显著边缘梯度增强的离散化(得到ΔI(u/v)Grad)的过程记作

ΔI(u/v)Grad=DiscretForEdgeGrad

(6)

2.1.3PSF的估计

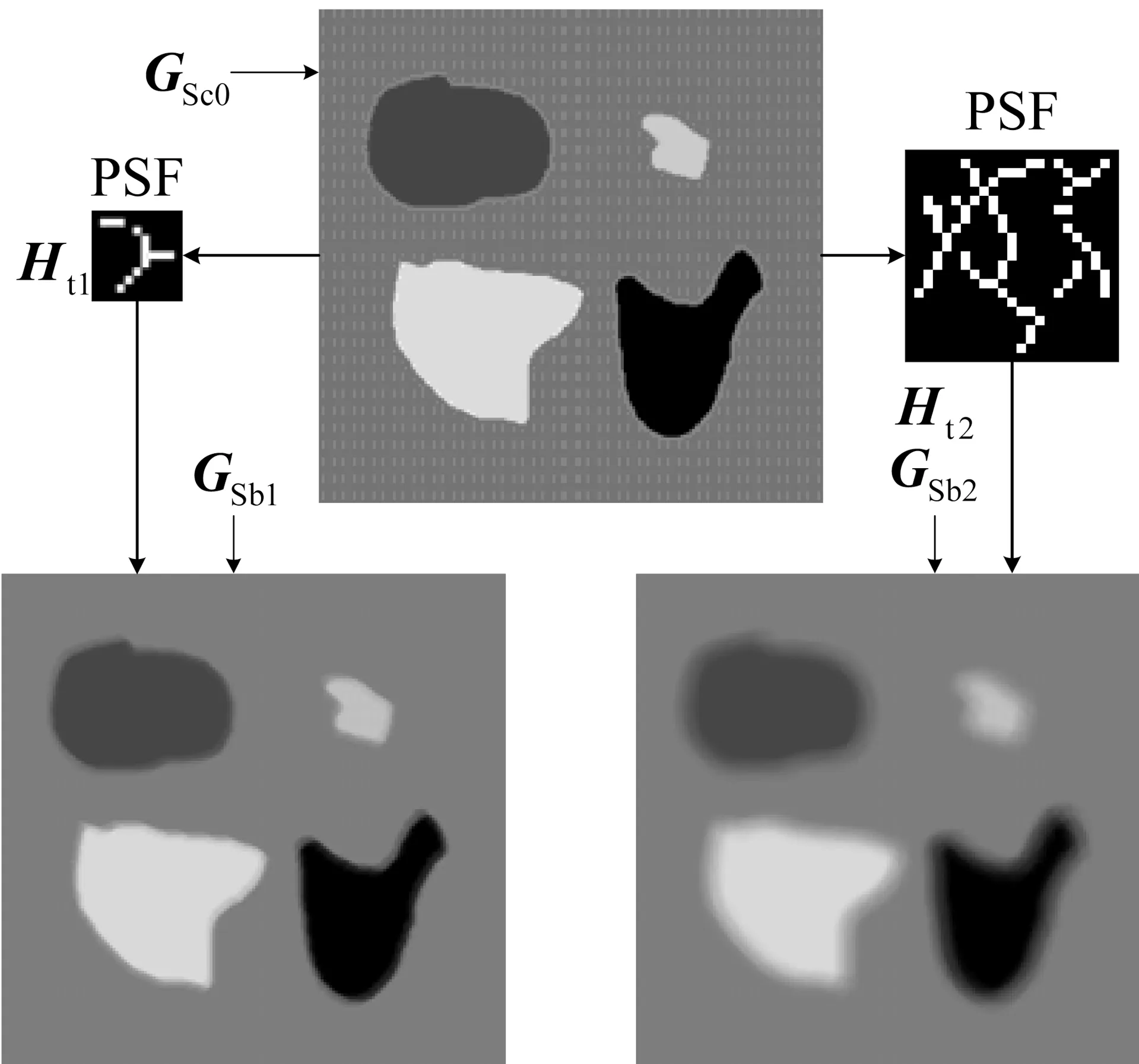
图2　基于增强边缘的模糊图像盲复原流程Fig.2　Flow of Image Blind Restoration with enhancing edges

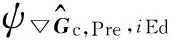
(7)

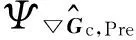
(8)

2.2递归残差修正方法

已有诸多学者采用残差图像方法抑制复原图像中的波动，然而，目前所研究的方法[7-8]尚不能适应预测图像错位的情形，并存在运算量大的问题。考虑到高分辨率图像的解模糊可利用低分辨率复原图像的特点，将显著错位的部分引入“预测图像”，设计了图像解模糊的递归残差修正方法。

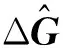
(9)

(10)

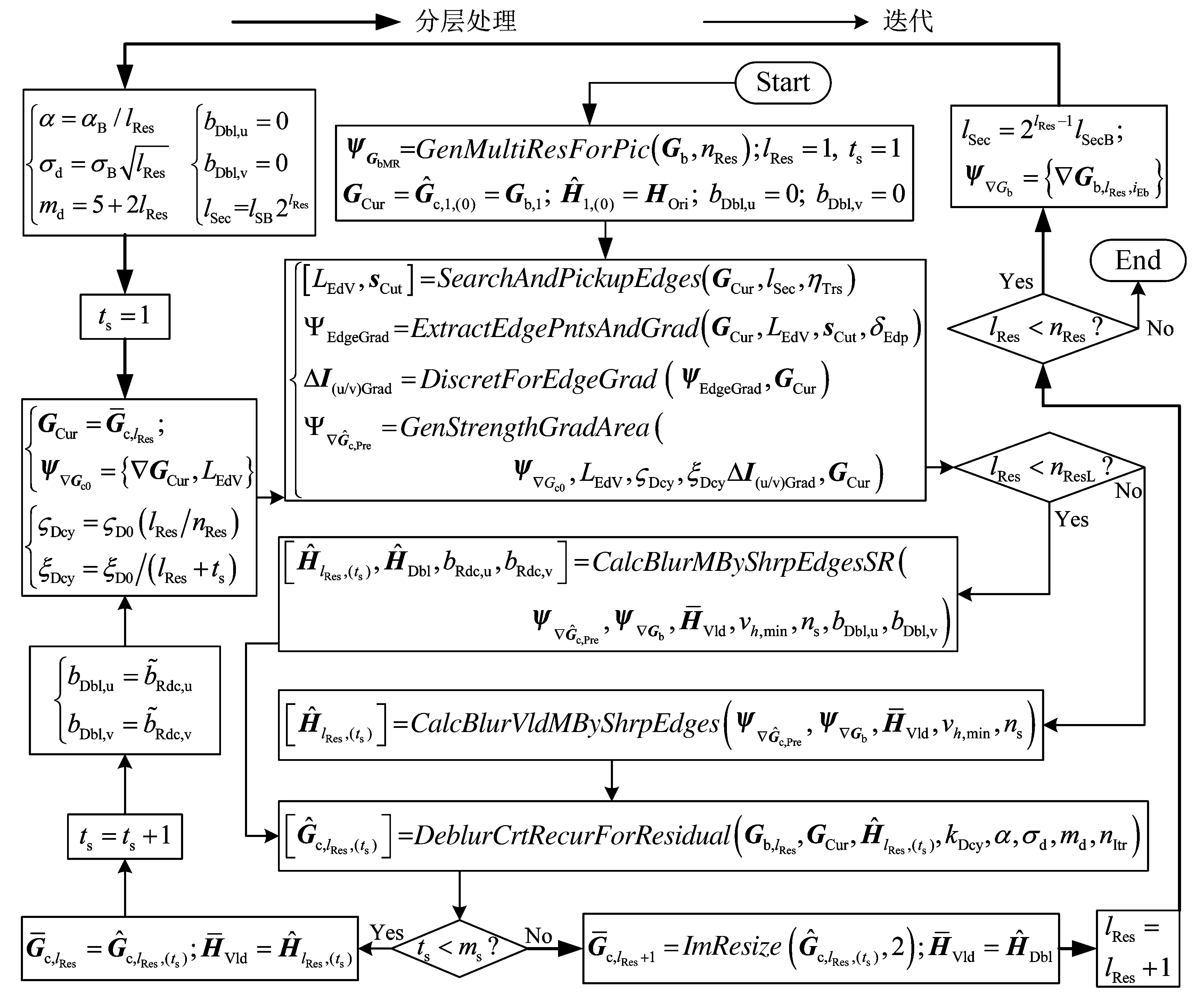
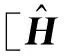
(10)式中：kLim为可调整的比例参数(0

文献[8]根据复原图像恢复中的波动主要是由图像中的边缘引起的这一特点，提出了残差图像解模糊中的增益修正方法。自适应增益的图像解模糊函数为

(11)

(12)

图3　已知PSF估计值时的递归残差修正流程Fig.3　Flow of recurrence residual algorithm

(13)

2.3分层迭代处理方法

图像分辨率不但直接决定了图像所含的信息量，同时也对图像处理算法的可靠性、精度及效率产生显著影响。对图像分辨率进行分层处理的方法已被广泛应用，其主要作用在于：①能逐层筛选显著目标以缩小执行处理算法的范围，从而提高处理效率；②能实现不同分辨率信息的分离以便于采用不同算法或设置不同参数来提升处理性能。图像复原分层迭代处理的详细流程如图4所示，可分为“分层处理”与“迭代”2部分。

图4　图像复原分层迭代处理算法的详细流程Fig.4　Flow of multi-layering with iteration algorithm

在该流程中，须设置以下4类参数：①整个处理流程的分层数和迭代次数：nResL,Ts；②搜索-增强显著边缘的参数：lSB,ηTrs,δEdp,ζD0,ξD0③PSF求解中的阈值和迭代次数：vh,min,ns；④解模糊中的增益调整系数，高斯滤波参数与优化迭代次数：kDcy,αB,σB,nItr。

图4中，函数ImResize若记为M1=ImResize(M0,kS)，其表示将矩阵(或图像)M0按尺度比例kS双线性插值变换为M1的函数(即图像尺度变换函数)。为便于算法设计，图像的尺度变换采用两分法，将图像的多尺度变换简记为

ΨGbMR=GenMultiResForPic(Gb,nResL),

(14)

(15)

边缘梯度离散化时，不可避免地弱化了显著边缘，影响了对PSF估计的精度。将PSF的超分辨率重构(super resolution，SR)估计算法简记为

CalcBlurMByShrpEdgesSR

(16)

对该算法的复杂度分析分为PSF估计和图像解模糊2部分。

PSF估计中，算法效率的优越性主要体现在图像显著边缘和PSF的局部处理上。该优化估计的计算量由构建的SGc(:,:,3)和LGb(3,:)决定。其中，SGc(:,:,3)为nb×nHVld矩阵；LGb(3,:)为1×nb向量；nb为显著边缘模糊邻域内点的总数；nHVld为PSF的有效像素个数。

设图像分辨率为nh×nw，PSF大小为du×dv，并记dm=[0.5(du+dv)]Floor，由Canny算子得到的显著边缘点数为λNtb(nh+nw)，估计过程中PSF的有效像素个数nHVld≤λVlddm，则nb≤kNtb(nh+nw)dm,kNtb=λNtb·λVld。对一般图像λNtb≤3且λVld≤5。因而，所构建的SGc(:,:,3)远小于直接构建的尺寸((nhnw)×(dudv))。

3仿真实验与分析

针对图像显著边缘的复原，采用Matlab工具箱自带图像“toyobjects.png”对本文提出的算法进行仿真验证。记仿真时的清晰图像为GSc0375×380。

3.1理想成像情况下的仿真验证

首先，在理想成像情况下对2幅在不同PSF下得到的模糊图像进行复原处理的仿真，如图5所示。其中，Ht1和Ht2分别为尺寸较小和较大的PSF，且Ht1和Ht2均不是等效的凸曲面。动态模糊仿真后得到GSb1375×380和GSb2375×380。

图5　具有显著边缘图像的动态模糊仿真Fig.5　Simulation results of the blurred imagewith obvious edges

这里分别对Ht1和Ht2所造成的模糊进行复原仿真验证。

3.1.1Ht1造成模糊的分层迭代复原仿真

由于Ht1的尺寸较小，边缘增强的偏差较小，因而不通过迭代即可得到边缘比较清晰的复原图像，PSF为Ht1时不同分辨率层次下的解模糊结果如图6所示。这里将分层迭代处理中的参数设置为

(17)

图6　PSF为Ht1时不同分辨率层次下的解模糊结果Fig.6　Image deblurring results when PSF is Ht1

从图6可以看出，对于Ht1造成的模糊图像，无须迭代(即Ts=1)即可经过3层分辨率(即nRes=3)中的解算得到PSF估计值和复原图像。

从图6还可以看出，PSF随着分辨率的提升而细化，最终接近Ht1。主要是因为本文算法在不同分辨率间的处理中，设计了与图像分辨率对应的PSF的尺度变换方法，利用尺度变换后的复原图像和PSF进行下一分辨率层次的迭代过程。说明本文算法既能在解模糊中抑制显著边缘引起的波动又能准确估计出PSF。

3.1.2Ht2造成模糊的分层迭代复原仿真

由于Ht2的尺寸较大，获得的边缘增强结果的偏差也较大，进而导致PSF矩阵估计值的偏差明显。因此，需要在每个分辨率层内进行迭代以逐步消除偏差，PSF为Ht2时，不同分辨率层次下的解模糊结果如图7所示，这里将分层迭代处理中的参数设置为

(18)

图7　PSF为Ht2时不同分辨率层次下的解模糊结果Fig.7　Image deblurring results when PSF is Ht2

分辨率为lRes=1,2,3及迭代次数为ts=1,2,3时的SGc(:,:,3)尺寸如表1所示。

表1　不同分辨率及迭代次数下的SGc(:,:,3)尺寸

对于视觉测量而言，复原图像与PSF质心所对应的原始图像之间的匹配性将显著影响测量精度，因此，这里对图像进行匹配性的验证，复原图像与原图的像素级匹配误差如图8所示。

图8中，图8a—图8c为现有算法结果，图8d为本文算法的匹配验证结果，可以看出，本文算法的匹配性图8d优于图8a—图8c。这里构建指标

(19)

进行量化对比。

图8a—图8d对应的fMatchErr代价值如(20)式所示，同样也表明了本文算法对图像复原的质量优于图8a—图8c。

(20)

图8　复原图像与原图的像素级匹配误差(显示为原误差值的4倍)Fig.8　Pixel level’s match error of different methods (four times than the original error)

3.2光照干扰情况下的仿真验证

在实际情况下，即使是含显著边缘的目标也往往会受到不均匀的光照，另外，成像过程中即使采用较低感光度也会引入噪声。因而，这里采用如(21)式的光照波动和成像噪声。

(21)

(21)式中：EGauss表示光照干扰情况下引入的高斯噪声；N(0,1×10-4)表示均值0，方差1×10-4的高斯噪声。光照扰动情况下的图像及其模糊加噪仿真如图9所示。

图9　光照扰动图像及其模糊加噪仿真Fig.9　Image with Gaussian white noises andun-ideal illumination

当采用双边滤波得到

(22)

然后，经过分层迭代处理(参数同3.1.2节中仿真实验的参数)可得如图10的仿真结果。

非理想光照条件下的仿真验证了本文算法对环境具有良好的适应性。

4结论

本文依据显著边缘的模糊特性在估计PSF中占主导地位这一特征，提出了一种显著边缘直接引导的动态模糊图像盲复原方法，能准确估计PSF并在图像解模糊中抑制显著边缘引起的波动。设计的算法主要包括基于显著边缘增强的PSF估计、图像解模糊的递归残差修正以及图像复原的分层迭代处理3部分。理想和非理想光照条件下的仿真结果表明，本文算法能高效地针对视觉测量中感兴趣的显著边缘信息进行图像复原，从而有利于保证视觉测量的精度与效率。

参考文献：

[1]程姝，赵志刚，吕慧显，等. 顺序结构的运动模糊图像复原技术综述[J].计算机应用，2013，33(S1)：161-165，185.

CHENGShu,ZHAOZhigang,LYUHuixian,etal.Surveyondeblurringtechnologyformotionimageswithsequencestructure[J].JournalofComputerApplication,2013,33(S1):161-165,185.

[2]刘卫华，白本督，赵小强.基于模糊相似度融合的图像复原算法[J].计算机辅助设计与图形学学报，2013，25(5)：616-621.

LIUWeihua,BAIBendu,ZHAOXiaoqiang.ImageRestorationAlgorithmBasedonFusionwithFuzzySimilarity[J].JournalofComputer-AidedDesign&ComputerGraphics,2013，25(5):616-621.

[3]周维华.Wiener滤波图像复原[J]. 计算机工程与科学，2007，29(3)：39-40，62.

ZHOUWeihua.ResearchontheWienerFilterImageDeblurring.[J].ComputerEngineering&Science,2007，29(3):39-40,62.

[4]肖宿，韩国强，沃焱，等.贝叶斯框架下的模糊图像盲区卷积算法(英文)[J].科学技术与工程，2010，10(14)：3344-3348.

XIAOSu,HANGuoqiang,WOYan,etal.BayesianFrameworkBasedBlindDeconvolutionAlgorithmforBlurredImage[J].ScienceTechnologyandEngineering, 2010, 10(14): 3344-3348.

[5]闫河，闫卫军，李唯唯.基于Lucy-Richardson算法的图像复原[J]. 计算机工程，2010，36(15)：204-220.

YANHe,YANWeijun,LIWeiwei.ImageRestorationBasedonLucy-RichardsonAlgorithm[J].ComputerEngineering,2010, 36(15):204-220.

[6]BANHAMMARKR,KATSAGGELOKS.Digitalimagerestoration[J].SignalProcessingMagazineIEEE, 1997,14(2): 24-41.

[7]YUANL,SUNJ,QUANL,etal.Progressiveinter-scaleandintra-scalenon-blindimagedeconvolution[J].ACMTransactionsonGraphics, 2008, 27(3): 1-10

[8]YUANL,SUNJ,QUANL,etal.Imagedeblurringwithblurred/noisyimagepairs[J].ACMTransactionsonGraphics, 2007, 26(3): 15-27.

[9]LUCYL.Aniterativetechniquefortherectificationofobserveddistributions[J].JournalofAstronomical, 1974, 79(6): 745-754.

Image blind restoration algorithm based on obvious edge feature

FU Qiang1, SUN Xiuxia1, LIU Shuguang1, XU Song2, PENG Ke1

(1. Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, P.R.China;2.Unit of 95910，Jiuquan 735018, P.R.China)

Abstract:For the problem of the imaging blurring caused by motion of the vehicle or vibration of the active vision plat in vision measurement, a new algorithm of image blind restoration is proposed by obvious edge feature. Firstly, an algorithm for searching and enhancing image edges is designed to overcome the drawbacks of the Canny algorithm. Further, a method of optimum estimation for the PSF is proposed only based on the neighborhood area of the obvious edges. Secondly, a recurrence residual algorithm is proposed for image deblurring, which can restrain the ringing of the restored image caused by obvious edges. Lastly, a multi-layering with iteration flow path is designed for guaranteeing the accuracy and reliability of the blind restoration. Experiments demonstrate that the method can reconstruct images and suppress the ringing effectively．The experiment under un-ideal illumination condition also shows the good adaptability against environment. This image restoration new algorithm can be efficient in practical application.

Keywords：blind restoration; obvious edges; point spread function(PSF); recurrence residual; multi-layering with iteration

DOI：10.3979/j.issn.1673-825X.2016.01.013

收稿日期：2015-02-14

修订日期：2015-10-13通讯作者：付强fuqiang931@126.com

基金项目：中国博士后科学基金(2014M562629)；陕西省自然科学基金(2014JM8332)

Foundation Items：The China Postdoctoral Science Foundation (2014M562629); The Natural Science Foundation Project of Shaanxi (2014JM8332)

中图分类号：TP391

文献标志码：A

文章编号：1673-825X(2016)01-0087-08

作者简介：

付强(1990-)，男，四川内江人，博士研究生，主要研究方向为无人机视觉导航与图像处理。E-mail:fuqiang931@126.com。

孙秀霞(1962-)，女，山东潍坊人，教授，博士生导师，主要研究方向为无人机导航与控制的理论及应用。E-mail:kgycw@163.com。

(编辑：王敏琦)