一种低通信开销联合时钟同步和定位算法

丁　进，林基明，周继华，赵　响，刘韦韦

(1.桂林电子科技大学 信息科学实验中心，桂林 541004; 2.重庆金美通信有限责任公司,重庆 400030)



一种低通信开销联合时钟同步和定位算法

丁进1，林基明1，周继华2，赵响1，刘韦韦1

(1.桂林电子科技大学 信息科学实验中心，桂林 541004; 2.重庆金美通信有限责任公司,重庆 400030)

摘要：针对无线传感器网络(wireless sensor networks ，WSNs)中降低节点间的通信开销的需求，提出一种基于成对广播同步协议(pairwise broadcast synchronization ，PBS)改进的联合时钟同步和定位算法。在联合时钟同步和定位过程中，锚节点(位置已知，时钟需同步)侦听未知节点(位置未知，时钟需同步)与参考节点(位置已知，时钟为参考时钟)双向交换的时间信息，不用发送额外的信息。因此相比于传统基于双向信息交换方式的联合时钟同步和定位算法可以节省大量的通信开销，同时可以降低同步所需参考节点的数目。该算法不仅对未知节点的位置参数和时钟参数进行联合估计，同时也完成锚节点时钟参数的估计。经过仿真分析，估计值满足所推导的克拉美罗下限(cramer-rao lower bound，CRLB)，且估计精度接近其他两种典型联合算法。综合考虑估计精度和通信开销，所提出的算法优于现有的联合时钟同步和定位算法。

关键词：无线传感器网络；联合时钟同步和定位；通信开销

0引言

在现代微型电子技术系统和无线通信技术快速发展的情况下，大量无线传感器设备构成的无线传感器网络(wireless sensor networks，WSNs)在目标定位和跟踪、目标速度估计、战场救援等方面得到广泛应用[1-2]，由于传感器节点体积小、成本低、计算能力和电源能量受限[3]等，因此出现许多亟待解决的关键问题。

时钟同步是WSNs中节点间信息正常收发、实现目标定位跟踪等应用的基础，近些年来得到快速发展，如参考广播同步协议[4]，传感器网络时钟同步协议[5]，洪泛时钟同步协议[6]等，其中节省大量通信开销的基于单双向[7]混合信息交换方式的时钟同步协议——成对广播同步协议(pairwise broadcast synchronization，PBS)[8-9]应用越来越广泛。节点定位在WSNs中确保对移动目标位置和突发事件位置精确定位，高精度节点定位算法主要是基于到达时间(time of arrival，TOA)[10]和基于到达时间差(time difference of arrival，TDOA)[11]2种测距方法，如基于TOA的最佳线性无偏估计定位算法[12]，基于TDOA的凹凸规划定位算法[13]等，但测距定位算法的先决条件是收发节点间保持严格时钟同步。

根据时钟同步和节点定位之间的密切关系，可以将时钟同步和节点定位放到同一个算法中解决，这类算法大致可分为两类：联合时钟同步与测距定位算法及联合时钟同步与免测距定位算法。在联合时钟同步与测距定位算法中，文献[14]利用参考节点分别和多个未知节点进行两两双向信息交换的方式；文献[15]对文献[14]进行扩展并提出一种非对称时间戳和被动侦听协议，主要以减少算法过程中未知节点反馈的信息数来降低通信开销，若要在文献[14-15]中获得未知节点的具体坐标，还需利用测距定位算法对距离参数进行处理，因此会产生误差积累。在联合时钟同步与免测距定位算法中，对未知节点进行联合时钟同步和节点定位算法[2]，利用多个参考节点分别与未知节点进行双向信息交换，可以获得较高的估计精度，但计算复杂度和通信开销相对较高；文献[16]利用未知节点与多个参考节点之间到达时间，利用加权先行最小二乘(weighted least square，WLS)估计方法对未知节点的时钟和位置参数进行联合估计的算法，通信开销较低且可以获得较高估计精度。

针对传感器节点低功耗和实际运行场景的需求，提出一种基于PBS系统模型联合时钟同步和节点定位算法，以延长传感器节点寿命且提高算法适应性，同时仿真结果显示算法的估计值满足相应的CRLB(cramer-rao lower bound)，且接近文献[2]和文献[16]所提出算法的估计精度。

1系统模型

对WSNs的时钟同步和定位算法分析，算法所需参考节点越少则适应性就越高，网络中节点收发信息越少则节点寿命越长。本文利用PBS协议中的信息交换模型来实现对未知节点的联合时钟同步和定位，算法需要的参考节点更少，无线传感器节点收发信息更少，并能同时完成时间同步和节点定位，可有效降低WSNs能耗，并提高算法灵活性。

算法基本模型如图1所示，由M个锚节点Ni(i=1,…,M)、1个参考节点R和1个未知节点S组成，其中，作为时间和位置基准的参考节点的位置信息为Pr=[xryr]T已知，待同步和定位的未知节点的时钟相偏θs和位置信息Ps=[xsys]T均未知，假设网络中有M个位置已知但时间未同步的锚节点Ni(i=1,…,M)侦听到参考节点和未知节点间交换的时间信息，其中各节点的时钟相偏分别为θi(i=1,…,M)未知，位置信息分别为Pi=[xiyi]T(i=1,…,M)已知，节点R与节点S进行双向的信息交换，锚节点Ni(i=1,…,M)对参考节点与未知节点间双向交换的信息进行单向侦听。

图1　节点间信息流向图示Fig.1　Flow of information between the nodes

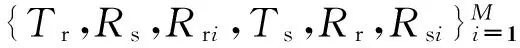
(1)

(2)

(3)

(4)

2算法详细介绍

2.1未知节点的联合时钟同步和定位

因节点间传播时延固定，对(1)—(4)进行处理后整理得

(5)

(5)式中，{ei,1,ei,2,ei,3,ei,4}(i=1,…,M)为服从独立高斯随机分布，令ei≡ei,4-ei,2，(i=1,…,M)，且服从均值为0方差为2σ2的高斯随机分布，又因tri已知，可令Ti=Rsi-Ts-Rri+Tr+tri，即有，

(6)

整理(6)式得

(7)

矩阵形式可写为

(8)

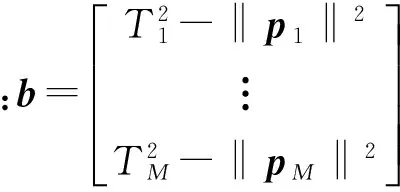
令Cw=E{wwT}/2σ2，也即

(9)

因此根据最小二乘估计方法(least square，LS)[17]可得

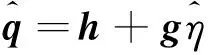
(10)

(11)

由(11)式可得

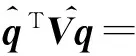
(12)

(13)

(14)

(15)

(16)

(注：经过大量仿真分析，发现满足上述条件且存在2个解时，采用(16)式解的精度更高，所以遇到上述存在2个解的情况，选择(16)式作为唯一解。)

(17)

④当(2gTVh-1)2-4gTVghTVh=0且gTVg≠0时，二次方程无解。这种情况只会发生在测量误差特别大的时候，也即环境特别恶劣的情况下。如果发生这种情况，可选用高精度时钟同步算法和节点定位算法分别对未知节点的时钟参数和位置参数进行求解。

2.2侦听节点的时钟同步

对方程(2)进行整理为

(18)

(18)式中，参考节点与锚节点间的传播时延tri已知，且噪声误差ei,2(i=1,…,M)服从均值为0方差为σ2的高斯随机分布，上述信息交换过程进行N次循环，对(18)式进行整理可得似然函数为

(19)

对方程(19)的对数进行求导可得，

(20)

由(20)式得锚节点Ni(i=1,…,M)时钟相偏的最大似然估计值为

(21)

2.3通信开销分析

基于高效最小而成联合时钟同步和节点定位算法[2]、基于WLS线性联合时钟同步和定位算法[16]、基于PBS时钟同步算法[8]和基于TOA的最佳线性无偏估计定位算法[12]分别与基于PBS协议的联合时钟同步和定位算法的通信开销进行比较。

基于高效最小二乘联合时钟同步和定位算法[2]中每个参考节点都需要与未知节点进行双向信息交换，因此需要发送和接收的信息总次数分别为NLSt=2NEL和NLSr=2NEL，其中E(E≥3)表示参考节点的数量，N(N≥3)表示未知节点与参考节点需要的信息交换总次数，L(一般设为1)表示未知节点的数量；基于WLS线性联合时钟同步和定位算法[16]中每个参考节点都需要向未知节点发送时间信息获得参考节点与未知节点之间的TOA，因此发送和接收的信息总次数分别为NWLSt=NEL和NWLSr=NEL；基于成对广播时钟同步协议(PBS)[8]中参考节点与某一个未知节点进行双向信息交换，其他位置节点侦听时间信息，因此发送和接收的信息总次数分别为NPBSt=2N和NPBSr=2N(M+1)，其中假设参考节点和未知节点的数量均为1；基于最佳线性无偏估计(BLUE)[12]的节点定位算法中节点间信息交换方式与文献[16]相似，因此发送和接收的信息总次数为NBLUEt=NEL和NBLUEr=NEL；基于PBS协议的联合时钟同步和定位算法需要发送和接收的信息总次数分别为Nt=2N和Nr=2N(M+1)，其中假设参考节点与未知节点的数量均为1，N表示参考节点与未知节点间信息交换的总次数。

综上所述，基于PBS协议的联合时钟同步和定位算法需要发送信息的通信开销最少，又因节点发送一条信息所需的能耗远大于节点接收一条信息所需要的能耗[18]，所以该算法在联合时钟同步和定位过程中需要的能耗最低，因此可以有效地延长传感器节点的寿命，与此同时相对于其他2种联合时钟同步和定位算法需要的参考节点数更少，具有更好的适应性。

3性能分析

3.1未知节点时钟相偏和位置参数估计值的CRLB

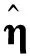
①当gTVg=0，

S=tr{QTQ}·2σ2

(22)

D=E{uTVu}

(23)

②当(2gTVh-1)2-4gTVghTVh=0且gTVg≠0，

(24)

(25)

③当(2gTVh-1)2-4gTVghTVh>0且gTVg≠0，

S=tr{QTQ}·2σ2

(26)

D=E{uTVu}

(27)

因此未知节点的时钟相偏和位置坐标参数估计值的CRLB分别为

(28)

(29)

3.2锚节点时钟相偏的CRLB

锚节点时钟相偏估计值的CRLB分析，对(20)式求二阶导得

(30)

因此，锚节点Ni(i=1,…,M)时钟相偏估计值的CRLB为

(31)

以上的性能分析在本文第4部分中进行仿真验证。通过观察仿真结果，算法所得到的估计值符合相应的CRLB。

4仿真分析

4.1本算法性能仿真

通过仿真验证本算法的有效性，假设在一个半径500 m的圆平面上随机分布6个无线传感器节点，其中包括一个参考节点(节点时钟作为参考时钟，节点位置已知)，4个锚节点(节点时钟的相偏未知，节点位置已知)，一个未知节点(节点时钟的相偏未知，节点位置未知)，其中未知节点与参考节点进行双向时间信息交换，4个锚节点侦听参考节点与未知节点交换的时间信息，这6个节点分别记录时间信息发送和到达的时间戳，在噪声方差逐渐增加情况下进行1 000次统计平均，图2表示本文所提出的算法的估计性能随噪声方差逐渐减小的情况下的变化曲线，以及其相应的CRLB。从图2中易得本文所提出的算法的估计精度满足其相应的CRLB。

图2　本文所提出算法的估计性能Fig.2　The estimation performance of the proposed algorithm

4.2估计精度的比较

基于PBS协议的联合时钟同步和定位算法分别与基于线性WLS的联合时钟同步和定位算法[16]和基于高效LS的联合时钟同步和定位算法[2]对未知节点的时钟和位置参数的估计精度进行对比，图3表示在相同的仿真环境下本文所提出的算法与另外两种算法的估计性能随噪声方差逐渐增加的变化曲线，由图3可得到本文所提出的算法接近另外2种算法的估计精度。

经观察上述仿真结果，基于PBS的联合时钟同步和节点定位算法的估计精度满足其CRLB，且接近其他两种联合时钟同步和定位算法相，文献[16]所提出算法需要4个参考节点和文献[2]所提出算法需要3个参考节点才可对一个未知节点进行时钟和位置参数的估计，而基于PBS的联合时钟同步和节点定位算法仅仅要求1个参考节点与4个锚节点即可实现未知节点进行时钟和位置参数的估计，因此适应性高于另外两种算法。

图3　3种算法估计性能比较Fig.3　Estimation performance comparison of three algorithms

5结论

本文提出一种基于成对广播同步协议的联合时钟同步和节点定位算法，仅需4个锚节点单向侦听参考节点与未知节点双向交换的时间信息即可对未知节点进行联合时钟同步和定位，同时也可实现对锚节点的时钟同步。因此在联合时钟同步和节点定位过程中节省大量的能耗和需要较少的参考节点，可以延长无线传感器节点寿命且具有更好的适应性。经过仿真分析，算法的估计性能满足其CRLB，同时可以获得接近文献[16]和文献[2]中的联合时钟同步和定位算法的估计精度。因此通过联合考虑通信开销与估计性能的关系，基于PBS的联合时钟同步和节点定位算法具有很好的性能。

参考文献：

[1]SERPEDIN E, CHAUDHARI Q M. Synchronization in wireless sensor networks[M]. United Kingdom: Cambridge, 2009.

[2]ZHENG J，WU Yikchung. Joint Time Synchronization and Localization of an Unknown Node in Wireless Sensor Networks[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1309-1320.

[3]雷建军，夏英，赵阔. 能量有效的无线传感器网络数据收集协议[J]. 重庆邮电大学学报：自然科学版，2014(10)：582-586.

LEI Jianjun, XIA Ying, ZHAO Kuo. Energy efficient data collection protocol for wireless sensor networks[J]. Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition, 2014, 26(5): 582-586.

[4]ELSON J, GIROD L, ESTRIN D. Fine-grained network time synchronization using reference broadcasts[C]//Proceedings of the 5th Symposium on Operating System Design and Implementation. Boston：[s.n] 2002: 147-163.

[5]GANERIWAL S, KUMAR R, SRIVASTAVA M B. Timing synch protocol for sensor networks[C]//Proceedings of 1st International Conference on Embedded Network Sensor Systems. Los Angeles：ACM, 2005: 138-149.

[7]LENG M, WU Yikchung. On Clock Synchronization Algorithms for Wireless Sensor Networks Under Unknown Delay[J]. IEEE Transactions on Vehicular Technology, 2010, 59(1): 182-190.

[8]NOH K L, SERPEDIN E, QARAQEM K. A New Approach for Time Synchronization in Wireless Sensor Networks: Pairwise Broadcast Synchronization[J]. IEEE Transactions on Wireless Communications, 2008, 7(9): 3318-3322.

[9]CAO Xuanyu, YANG Feng, CAN Xiaoying. Joint Estimation of Clock Skew and Offset in Pairwise Broadcast Synchronization Mechanism[J]. IEEE Transaction Communication, 2013, 61(6): 2508-2521.

[10] CAFFERY J J. A new approach to the geometry of TOA location[C]//Proc. 52nd IEEE Vehicular Technology Conference(VTC). [s.l.]:IEEE Press, 2000: 1943-1949.

[11] GHOLAMI M R,GEZICI S, STRÖOM E G. TDOA Based Positioning in the Presence of Unknown Clock Skew[J]. IEEE Transaction on Communication, 2013, 61(6): 2522-2534.

[12] CHAN F K W, SO H C, ZHENG J, et al. Best linear unbiased estimator approach for time-of-arrival based localization[J]. IET Signal Processing, 2008, 2(2): 156-162.

[13] GHOLAMI M R, GEZICI S, STRÖM E G. A Concave-Convex Procedure for TDOA Based Positioning[J]. IEEE Communications Letters, 2013, 17(4): 765-768.

[14] RAJAN R T, VEEN A J. Joint ranging and clock synchronization for a wireless network[C]∥Proceedings in 4th IEEE Int. Workshop Computer Advances in Multi-Sensor Adaptive Process. [s.l.]:IEEE, 2011: 297-300.

[15] CHEPURI S P, RAJAN R T, LEUS G, et al. Joint clock synchronization and ranging: Asymmetrical time-stamping and passive listening[J]. IEEE Signal Processing Letter, 2013, 20(1): 51-54.

[16] ZHU Shouhong，DING Zhiguo. Joint Synchronization and Localization Using TOAs: A Linearization Based WLS Solution[J]. IEEE Journal on Selected Areas in Communication, 2010, 28(7): 1016-1015.

[17] KAY S M. Fundamentals of statistical signal processing: estimation theory[M]. USA: Prentice-Hall, Inc., 1993.

[18] GAO Q, BLOW K J, HOLDING D J, et al. Radio range adjustment for energy efficient wireless sensor networks[J]. Ad Hoc Networks, 2006, 4(1): 75-82.

A joint clock synchronization and localization algorithm with low communication overhead

DING Jin1, LIN Jiming1, ZHOU Jihua2, ZHAO Xiang1, LIU Weiwei1

(1.Guangxi Experiment Center of Information Science, Guilin University of Electronic Technology, Guilin 541004,P.R. China;2.Chongqing Jinmei Communication Co., Ltd, Chongqing 400030, P.R.China)

Abstract:Aiming at the demand of reducing the communication overhead in wireless sensor networks(WSNs), we propose a joint clock synchronization and localization algorithm based on modified pairwise broadcast synchronization (PBS) protocol. In our proposed scheme, anchor nodes (unknown clock bias and known position) overhear the timing message exchanges of reference node (known clock bias and known position) and unknown node (unknown clock bias and unknown position) without sending extra messages. So the proposed algorithm can reduce more communication overhead and require less reference nodes than those algorithms based on two-way message exchanges model. In the proposed algorithm, we obtain estimators of clock and localization parameters of unknown node, the estimators of clock parameters of anchor nodes. Via analyzing and simulating its estimation performance, we can find the estimation performance of the proposed algorithm meets these cramer-rao lower bound(CRLB) and is close to the estimation performance of other two available algorithms. Considering the tradeoff between the estimation performance and communication overhead, we can see that this algorithm performs better than the available joint clock synchronization and localization algorithms.

Keywords：wireless sensor networks; joint clock synchronization and localization; communication overhead

DOI：10.3979/j.issn.1673-825X.2016.01.005

收稿日期：2014-09-16

修订日期：2015-01-05通讯作者：丁进flying-dj@live.com

基金项目：国家自然科学基金项目(61172054,61362006)；广西自然科学基金项目(2014GXNSFAA118387, 2013GXNSFAA019334)；桂林电子科技大学研究生创新项目(GDYCSZ201409)。

Foundation Item：National Natural Science Foundation of China (61172054 and 61362006)； The Guangxi Natural Science Foundation (2013GXNSFAA019334); The Innovation Project of GUET Graduate Education (GDYCSZ201409).

中图分类号：TN929

文献标志码：A

文章编号：1673-825X(2016)01-0030-07

作者简介：

丁进(1988-)，河北石家庄人，男，硕士研究生，主要研究方向为无线传感器网络时钟和节点定位。E-mail：flying-dj@live.com。

林基明(1970-)，四川三台人，男，教授，博士生导师，主要研究方向为无线通信技术。E-mail：linjm@guet.edu.cn。

周继华(1979-)，重庆忠县人，男，正高级工程师，博士，主要研究方向为LTE定位技术。E-mail：jhzhou@ict.ac.cn。

赵响(1979-)，女，河北晋州人，讲师，硕士，主要研究方向为无线传感器网络中的定位与同步。E-mail: zhxiang@guet.edu.cn。

刘韦韦(1986-)，江西九江人，男，硕士研究生，主要研究方向为LTE测距技术。Email：liuweiwei19861123@163.com。

(编辑：张诚)