基于改进自监督学习群体智能(ISLCI)的高性能聚类算法

曾令伟, 伍振兴, 杜文才

(1. 琼州学院 电子信息工程学院, 海南 三亚 572022; 2. 海南大学 信息科学技术学院, 海南 海口 570228)



基于改进自监督学习群体智能(ISLCI)的高性能聚类算法

曾令伟1, 伍振兴1, 杜文才2

(1. 琼州学院 电子信息工程学院, 海南 三亚 572022; 2. 海南大学 信息科学技术学院, 海南 海口 570228)

摘要：针对现有数据聚类算法(如K-means)易陷入局部最优和聚类质量不佳的问题，提出一种结合改进自监督学习群体智能(improved self supervised learning collection intelligence，ISLCI)和K均值(K-means)的高性能聚类算法。已有的自监督学习群体智能演化方案具有计算效率和聚类质量高的优点，但当应用于数据聚类时，收敛速度较慢且极易陷入局部最优。为ISLCI加入突变操作，增加其样本多样性来降低早熟的概率,提高最优解的求解质量；计算每个样本的行为方程，获得其行为结果；通过轮盘赌方案来选择群体智能学习的对象和群体中其他样本学习目标对象的属性来提高自己。同时，利用K-means操作提高其收敛速度，提高算法计算效率。对比试验结果表明，本算法具有收敛速度快、聚类质量高、不易陷入局部最优的特点。

关键词：自监督学习群体智能；数据聚类；突变操作；簇内距离；函数评价次数

0引言

将数据集合按照相似性进行分类，相似性高的数据归为一簇，此为数据挖掘中的聚类技术[1]，聚类技术是数据挖掘的核心技术之一。聚类通常分为基于密度聚类[2]、分割聚类[3]、分层聚类[4]等。

已有大量针对数据挖掘聚类的研究，文献[5]提出一种基于图划分的高阶联合聚类算法(based on gragh partitioning of high order combined clustering algorithm,GPHCC)，该算法将网状高阶异构数据的聚类问题转化为多对二部图的最小正则割划分问题。通过将优化问题转化为半正定问题求解，降低了计算复杂度，然而收敛速度依然不够理想。文献[6]提出了基于多子群粒子群伪均值(PK-means)聚类算法，而该算法的收敛速度不佳。文献[7]提出了一种基于混合差分进化的滑动窗口数据流聚类算法。该算法在对数据流执行聚类时具有较高的执行效率，但对于非数据对象时，分类质量不够理想。文献[8]提出一种由在顶点上的低层随机游走和在组件上的高层随机游走2部分构成的双层随机游走半监督聚类算法，其算法仅优于其他半监督聚类算法，而其他高质量聚类算法并无明显优势。文献[9]提出了1种基于2个最小生成树命中时间的高维数据聚类算法，该算法收敛速度快，然而容易陷入局部最优。文献[10]提出一种基于人工蚁群算法的数据挖掘聚类优化算法，而其同样具有收敛速度不佳及容易陷入局部最优的不足。文献[11]基于遗传算法与混沌理论提出了一种优化聚类算法，该算法具有收敛速度快、计算复杂度低的优点，但其较容易陷入局部最优。文献[12]针对数据流提出了一种收敛速度优化的算法，而其具有收敛早熟概率大的缺点。

文献[13]提出了一种基于自监督学习的启发式优化算法(self supervised learning collection intelligence,SLCI)，该研究针对一些经典问题做了试验验证并与部分经典优化算法进行了比较，结果表明其具有计算效率高、聚类质量高的优点。本文将该优化算法引入数据挖掘的聚类算法中，并结合经典的K-means算法[14]，提出了一种收敛速度快、求解质量高及不易早熟收敛的聚类算法，并通过对比试验验证了以上特点。

1K-means聚类算法

设R=[Y1,Y2,…,YN](其中Yi∈RD)表示含N个数据对象的集合，S=[X1,X2,…,XK]表示该集合的K个簇。聚类过程即为将R中数据全部分配至K个簇中。簇内方差定义为簇内各Yi与质心Xj的欧氏距离平方和，该目标方程如下表示

(1)

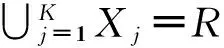
假设预知簇数量，K-means算法的目标是计算并确定各簇的质心。K-means算法的主要步骤如下。

1)从数据集R=[Y1,Y2,…,YN]中随机选取K个样本作为初始化质心S=[X1,X2,…,XK]。

2)将R中各样本分配至距离最近的质心。

3)重新计算各簇质心位置。

4)重复2)—3)步，直至满足预设的结束条件。

文献[15]提出了K-means的优化算法，称为K-means++算法，其步骤如下。

1)从R中均匀随机的选取一个中心X1。

2)对每个样本Yi，计算其与最近中心的距离D(Yi)。

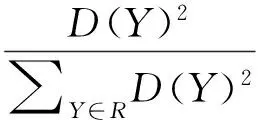
4)重复2)—3)步，直至质心数量达到K。

5)至此，选取了全部的初始化质心，然后使用标准K-means算法进行聚类处理。

2SLCI优化算法

文献[13]提出了一种基于自监督学习的群体智能优化算法，该算法源自社会中同类人群具有互相学习的趋势，同类人群指该人群具有内在共通的目标，其中每个人学习其他同类人群来提高自己。最终每个人学习其他同类人并经过数次迭代后提高了群体的总性能。如果数次迭代后，群体并无改善，该群体则称为饱和状。

一般无约束最小值问题表示为

Minimizef(X)=f(x1,x2,…,xi,…,xN)

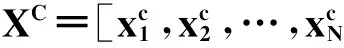
步骤1初始化以下参数：样本C的数量、属性的采样间隔ψi、采样间隔缩减系数r∈[0,1]、收敛参数ε、迭代次数n和变化次数t。

步骤2每个样本c选择行为f*(Xc)的概率计算为

(2)

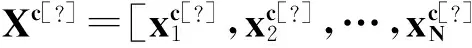
(3)

(3)式中，ψi=(‖ψi‖)×r。

步骤5在缩短后的采样周期内采样t个行为并组成集合，即Fc,t=[f(Xc)1,f(Xc)2,…,f(Xc)t]，从中选择最佳行为f*(Xc)。其他样本学习该最优行为，表示为

步骤6如f*(Xc)较之前无明显改善，该群体则视作饱和，即多次迭代后，行为间差异不大于阈值ε，表示为

(4)

(5)

(6)

步骤7满足以下2个条件之一即结束，否则跳至步骤2。

1)达到迭代最大次数限制。

2)如果该群体饱和，即满足方程(4)—(6)。

3SLCI的改进算法ISLCI

本文对文献[13]算法进行改进，提出了ISLCI(improvedselfsupervisedlearningcollectionintelligence)算法，提高其正确率与收敛速度，SLCI算法当收敛于局部最优或搜索速度过慢时，易早熟收敛。本文提出一种突变机制扩大其搜索范围以及增加解的多样性来防止早熟。

(7)

(7)式中，变量m1，m2，m3是随机选择的3个样本，所以m1≠m2≠m3≠c。

(8)

所选样本则为

(9)

(10)

(10)式中：z=1,2,…,b；rand(.)表示[0,1]间的随机数；γ表示小于1的随机数；D表示数据对象的维度。因此，基于如下方程选择第i次迭代时c的新增属性

(11)

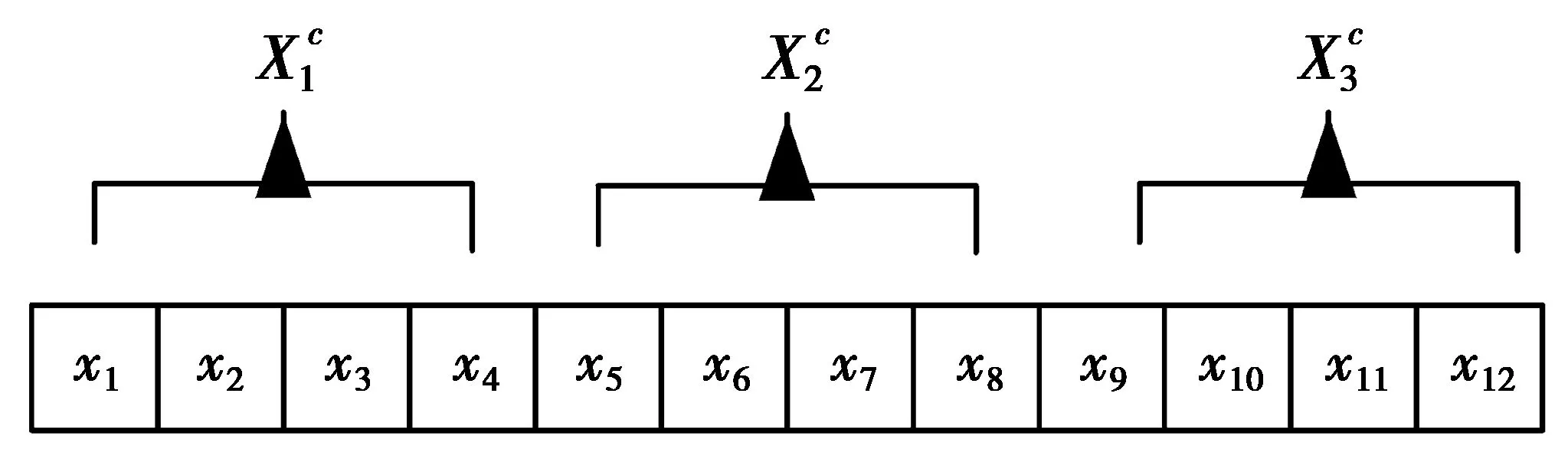
图1　样本聚类方案举例Fig.1　Individuality clustering approach sample

4融合K-means与ISLCI的聚类算法K-ISLCI

ISLCI具有分类质量高和不易早熟的优点，结合K-means提高收敛速度，提出了一种高性能的数据挖掘聚类算法K-ISLCI。首先利用K-means算法处理样本，然后运行ISLCI算法处理。本算法具有收敛速度快，不易陷入局部最优和分类准确率高的优点。算法步骤如下。

步骤1产生初始化样本，利用(12)式随机产生C个初始样本

(12)

(13)

(14)

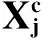
(15)

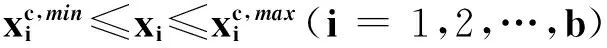
步骤2使用第1节的K-means算法处理每个样本。

步骤3使用第3节的ISLCI算法处理每个样本。

步骤4使用(1)式计算每个样本的行为方程f(Sc)。

步骤5使用(2)式计算每个样本选择行为f*(Sc)的概率。

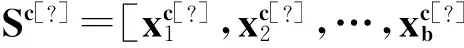
步骤8如f*(Xc)较之前无明显改善，该群体则视作饱和，即多次迭代后，行为间差异不大于阈值ε。

步骤9满足以下2个条件之一即结束，否则跳至步骤2。

1)达到迭代最大次数限制。

2)如果该群体饱和，即满足方程(4)—(6)。

5试验结果与分析

选择6个真实、经典数据集验证本算法，介绍如下。

1)Irisdataset(N=150,D=4,K=3)：以鸢尾花特征作为数据源，共150个数据，分为3类(setosa，versicolor，virginica)，每类50个数据，每个数据含4个属性。

2)Winedataset(N=178,D=13,K=3)：以酒的化学成分作数据源，共178个数据，分为3类，样本个数分别为59，71，48，每个数据含13个属性。

3)Glassdataset(N=214,D=9,K=6)：以玻璃的特征作为数据源，共214个数据，分为6类，样本个数分别为70，76，17，13，9，29，每个数据含9个属性。

4)BreastCancerWisconsindataset(N=683,D=9,K=2)：共683个数据集，分为2类，样本数量分别为444，239，各数据含9个属性。

5)Voweldataset(N=871,D=3,K=6)：共871个数据集，分为6类，样本数量分别为72，89，172，151，207，180，各数据含3个属性。

6)ContraceptiveMethodChoicedataset(N=1 473,D=9,K=3)：共1473个数据集，分为3类，样本数量分别为629，334，510，各数据含9个属性。

采用2个参数评价聚类算法的性能，分别为i)簇内距离，如(1)式定义；ii)目标函数评价次数适应度函数评估( fitness function evaluation, NFE)。簇内距离越小表示聚类质量越高；NFE表示搜索最优值过程中，聚类算法计算目标方程(1)式的次数，NFE值越小表示收敛速度越快。

试验环境为PC(Intel Core i7-3770, 3.4 GHz, 4 GByte内存)，操作系统为Windows 7专业版，编程环境为Matlab 2007。K-ISLCI，ISLCI和SLCI的参数如表1所示。将本算法与以下各聚类算法进行对比试验：K-means，K-means++[15]，一般的蜂群算法(general artificial bee colony, GA)[10]，遗传算法案例 (sample of a genetic algorithm, SAA)[11]，快速聚类算法 ( data speedup clustering, DS)[12]滑动窗口优化的聚类算法(clustering algorithm optimized for sliding window, COS)[7]，基于树结构优化的混合算法 (hybrid tree based optimized algorithm , HBOA)[9]。将以上各聚类算法分别对6个数据库进行聚类实验，每个实验均运行20次，将所得20个聚类实验结果(簇内距离)中最优值、平均值、最差值、标准差和NFE值统计于表2中。

表2中可看出，对于Iris数集，K-ISLCI和ISLCI算法每次运行均可收敛于全局最优值96.555 4，而SLCI，K-Means，K-means++，GA，SAA，DS，COS和HBOA的最优值分别为96.655 7，97.325 9，97.325 9，113.986 5，97.457 3，97.365 9，97.100 7和96.752；同时K-ISLCI的标准差是0，远低于其他算法，可见本算法的聚类质量和鲁棒性均明显优于其他聚类算法。对于Wine数据集，K-ISLCI的最优值同样最佳，同时平均值、最差值均优于其他算法。对于UCI的一个数据集(contraceptive method choice, CMC)，K-ISLCI获得最优簇内距离5 693.73，而SLCI，ISLCI，K-Means，K-means++，GA，SAA，DS，COS，HBOA的最优值分别为5 695.33， 5 694.28， 5 703.20，5 703.20，5 705.63，5 849.03，5 885.06，5 701.92，5 699.26，此外，K-ISLCI的标准差也明显优于其他算法。对于vowel数据集，本算法的最优、平均、最差簇内距离和标准差分别为48 967.24，148 987.55，149 048.58，36.086，同样明显小于其他算法。

比较表2中的ISLCI和SLCI的试验结果：对于Wine数据集，ISLCI的最优、平均、最差值分别为16 295.16，16 296.51，16 297.98，标准差为0.907；而SLCI的最优、平均、最差结果分别为16 298.01，16 300.98，16 305.60，标准差为2.118。可见本文的突变操作提高了SLCI的聚类性能。

比较表2中K-ISLCI，ISLCI，SLCI，可看出将K-means加入ISLCI，具有明显效果。对Wine数据集，K-ISLCI，ISLCI，SLCI的全局最优值分别为16 292.44，16 295.16，16 298.01。结果证明K-ISLCI比ISLCI和SLCI具有更好的聚类性能。此外，结合K-means增强了算法收敛速度。对于Wine数据集，SLCI和ISLCI获得最优解分别需17 500和16 500次计算，而K-ISLCI仅需6 250次计算即可获得最优解，因此K-ISLCI收敛速度较快。尽管K-means和K-means++算法收敛快于其他算法，但其较容易早熟，例如，对于Wine数据集，K-means++算法仅需261次计算即可获得最优解，但其收敛结果明显比K-ISLCI差。

综上所述，表2的试验结果证明了，相较于其他算法，本算法可在较低的标准差及较少的计算次数下获得了更佳的聚类效果。表3—5所示为K-ISLCI获取的各数据集质心，可看出本聚类算法成功获得所有数据集的质心，可看出本算法的有效性，所获得质心供参考。

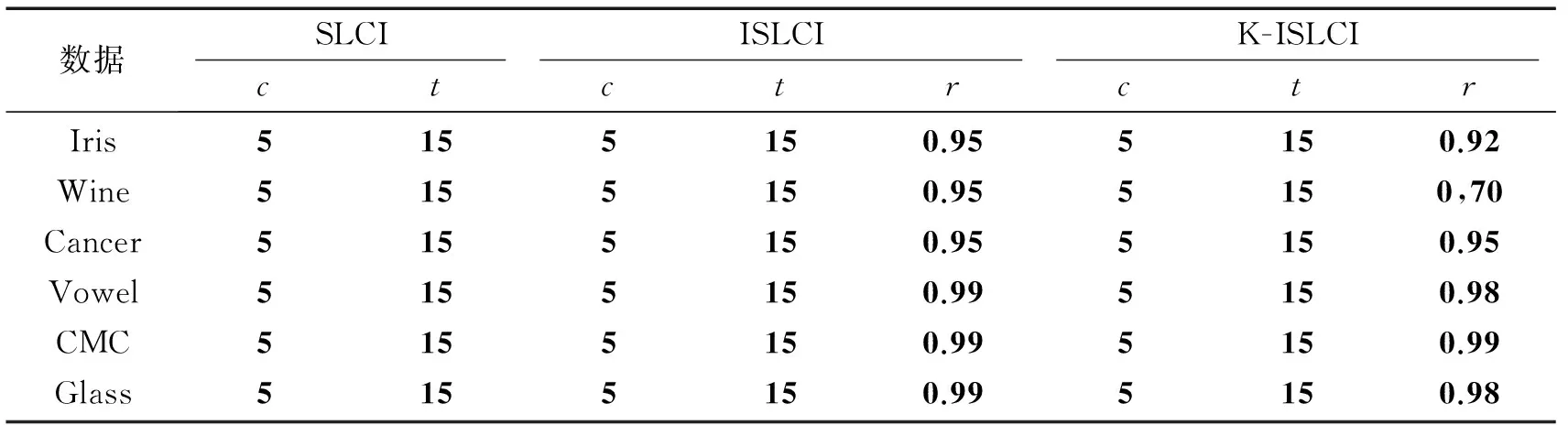
表1　SLCI，ISLCI，K-ISLCI算法参数(c(每个队列中样本数量)、t(样本属性的数量)、r(采样周期的折减系数))

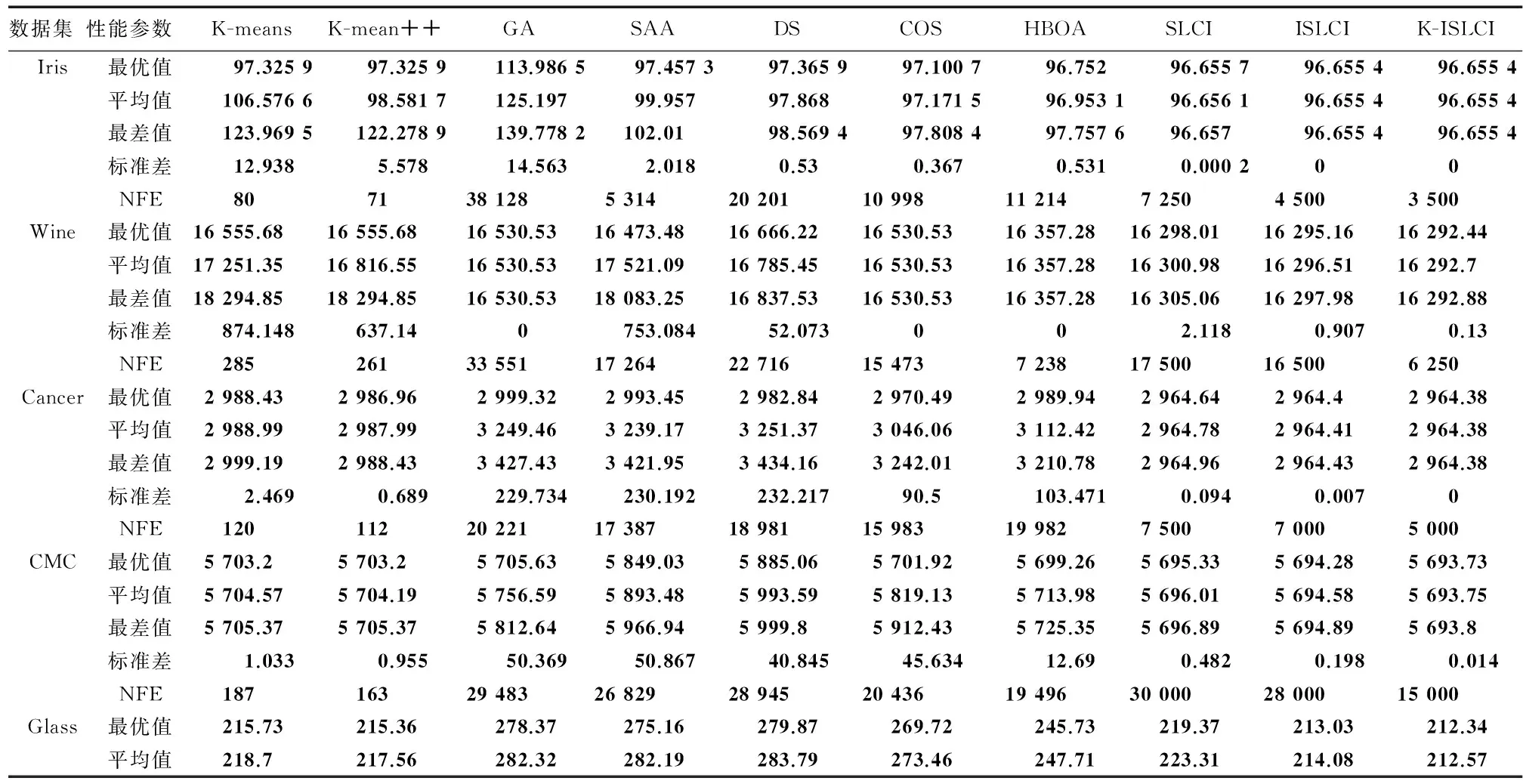
表2　各聚类算法实验结果

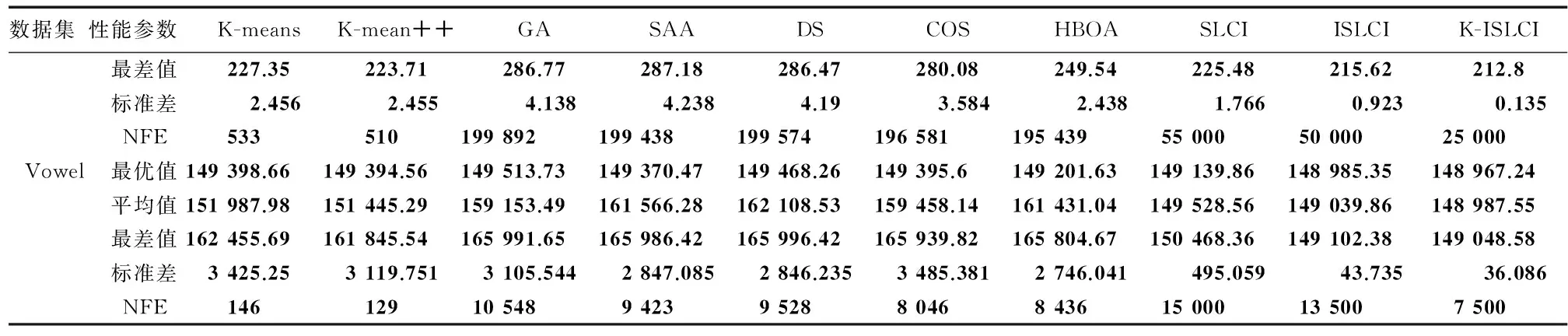
续表2

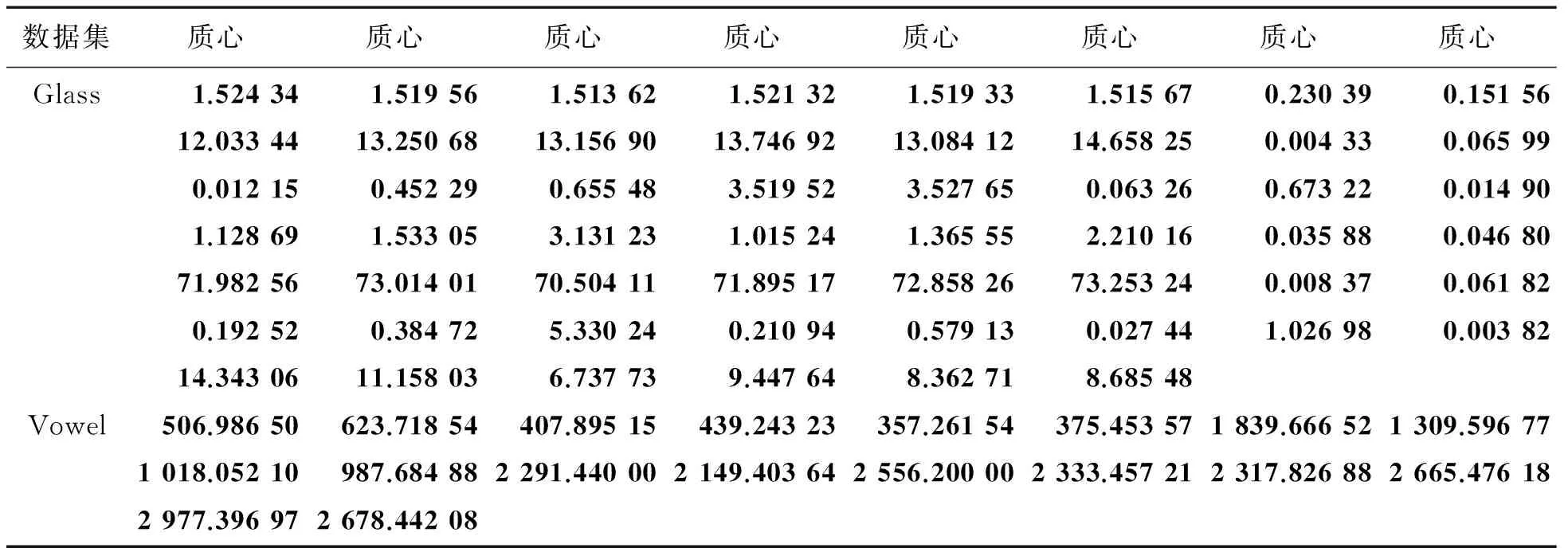
表3　Glass与Vowel各类的质心

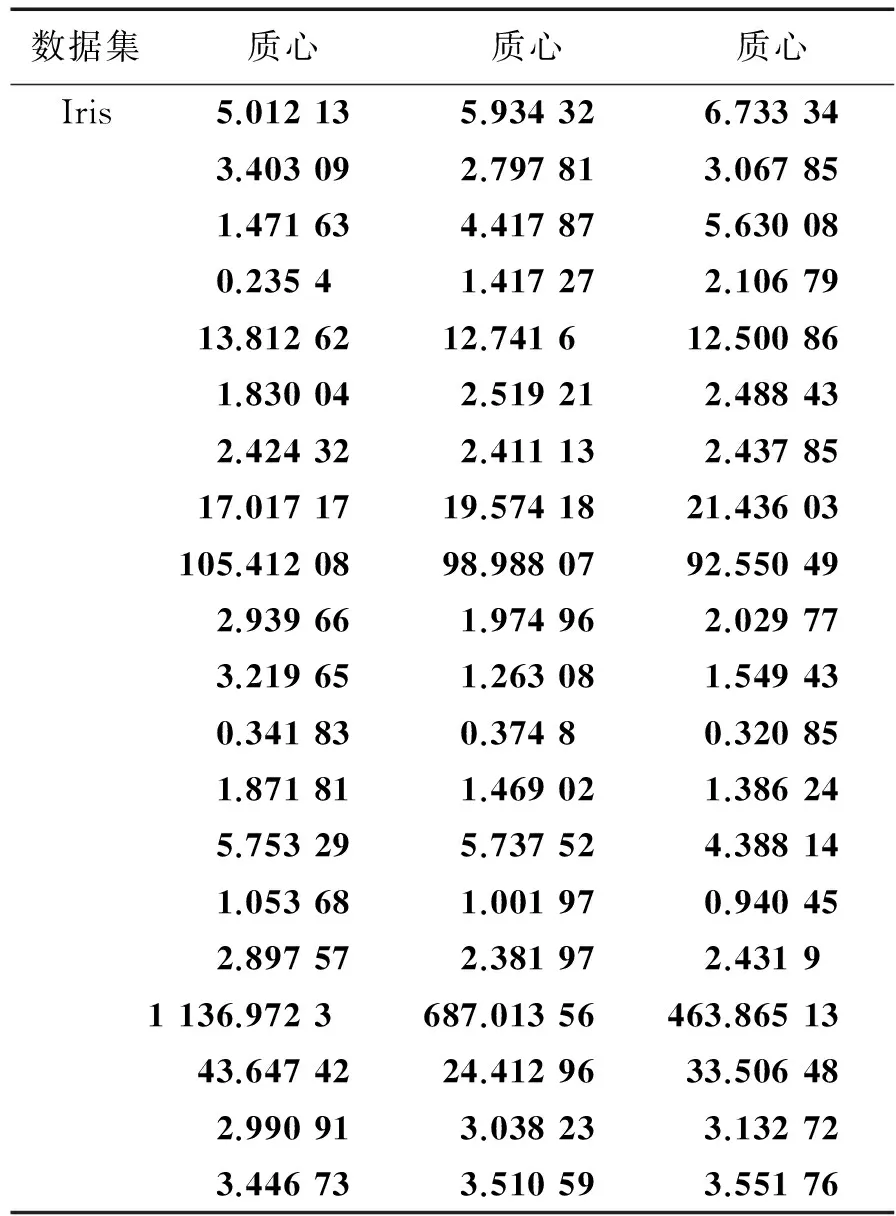
表4　Iris各类的质心

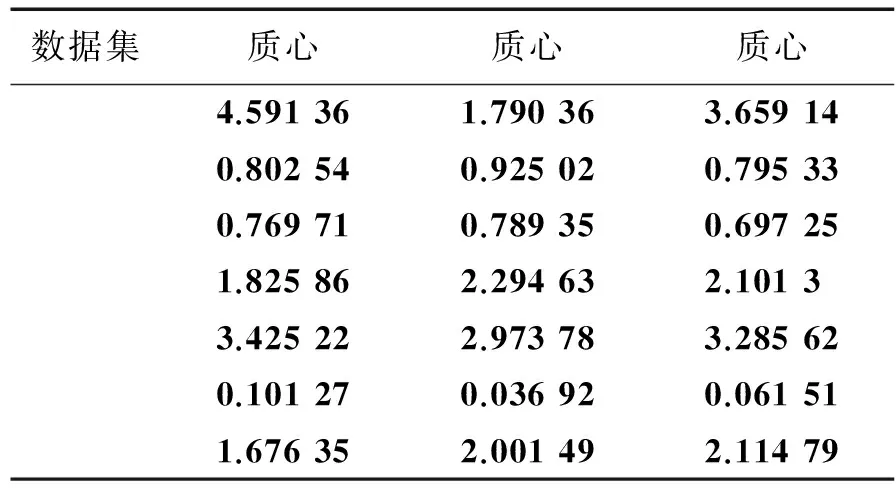
续表4

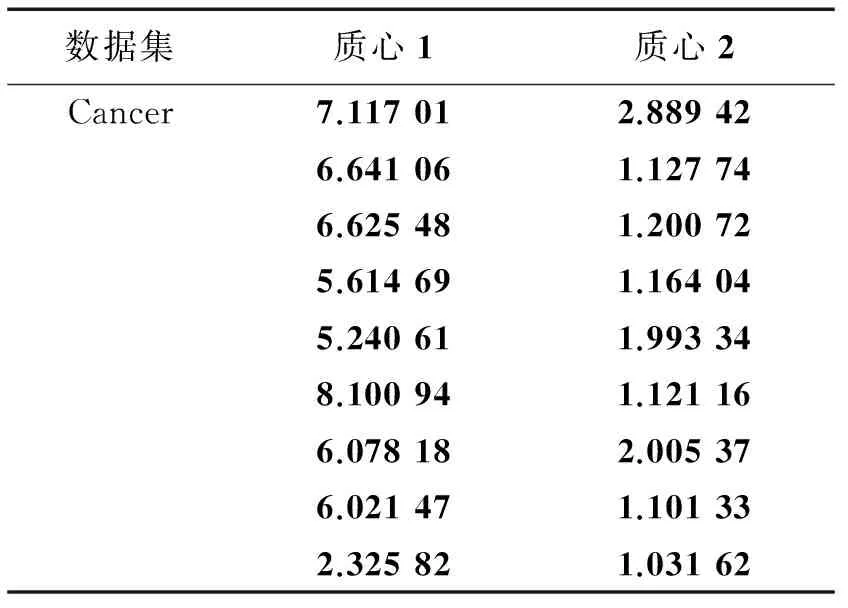
表5　Cancer各类的质心

6结束语

SLCI是一种新型的高性能优化算法，对于数据挖掘聚类算法具有极大的潜力。然而，SLCI的收敛速度不佳，当数据维度增加或簇数量增加时，容易产生陷入局部最优。针对此类缺点，结合突变操作提出了一种改进的ISLCI算法，扩大其搜索范围来降低早熟收敛的概率，此外，结合K-means算法提高其收敛速度。试验结果表明，本算法具有收敛速度快、聚类质量高、不易陷入局部最优的特点。

本算法需预知数据集部分参数，未来将对此开发新的自适应聚类算法，提高算法的实用性。

参考文献：

[1]毕志升, 王甲海, 印鉴. 基于差分演化算法的软子空间聚类[J]. 计算机学报, 2012, 35(10): 2116-2128.

BI Zhisheng , WANG Jiahai , YIN Jian. Subspace Clustering Based on Differential Evolution[J].Chinese Journal of Computers,2012,35(10): 2116-2128.

[2]马素琴, 施化吉. 阈值优化的文本密度聚类算法[J]. 计算机工程与应用, 2011, 47(17): 134-136.

MA Suqin,SHI Huaji. Text density clustering algorithm with optimized threshold values[J].Computer Engineering and Applications,2011,47(17):134-136.

[3]张薇,刘加.电话语音的多说话人分割聚类研究[J].清华大学学报：自然科学版,2008,48(4):574-577.ZHANG Wei,LIU Jia. Multi-speaker segmentation and clustering of telephone speech[J].Journal of Tsinghua University:Science and Technology,2008,48(4):574-577.

[4]许宁,张毅坤.基于正交分层聚类算法软件可靠性模型的预测分析[J].计算机应用,2007,27(3):635-637.XU Ning,ZHANG Yikun. Research on reliability prediction model based on orthogonal layer-clustering algorithm[J].Journal of Computer Applications,2007,27(3):635-637.

[5]杨欣欣,黄少滨.基于图划分的网状高阶异构数据联合聚类算法[J].四川大学学报:工程科学版,2014,46(2):105-110.

YANG Xinxin， HUANG Shaobin. A Net-structure High-order Heterogeneous Data Co-clustering[J].Journal of Sichuan University:Engineering Science Edition,2014,46(2):105-110.

[6]沈艳, 余冬华, 王昊雷. 粒子群 K-means 聚类算法的改进[J]. Computer Engineering and Applications, 2014, 50(21): 125-128.SHEN Yan,YU Donghua,WANG Haolei. Improvement of K-means based on particle swarm clustering algorithm[J].Computer Engineering and Applications,2014(21):125-128.

[7]任永功,胡志冬,杨雪.基于混合差分进化的滑动窗口数据流聚类算法研究[J].计算机应用研究,2014,31(4):1009-1012.

REN Yonggong;HU Zhidong;YANG Xue.Research on sliding window data stream clustering algorithm based on hybrid differential evolution[J].Application Research of Computers,2014,31(4):1009-1012.

[8]何萍,徐晓华,陆林,等.双层随机游走半监督聚类[J].软件学报,2014,25(5):997-1013.

HE Ping,XU Xiaohu,LU Lin, et al.Semi-Supervised Clustering via Two-Level Random Walk[J].Journal of Software,2014,25(5):997-1013.

[9]GALLUCCIO L, MICHEL O, COMON P, et al. Clustering with a new distance measure based on a dual-rooted tree[J]. Information Sciences, 2013(251): 96-113.

[10] KARABOGA D, OZTURK C. A novel clustering approach: Artificial Bee Colony (ABC) algorithm[J]. Applied Soft Computing, 2011, 11(1): 652-657.

[11] LEE J, LEE D. An Improved Cluster Labeling Method for Support Vector Clustering[J]. IEEE Transactions on pattern analysis and machine intelligence, 2005, 27(3): 461-464.

[12] FU L, NIU B, ZHU Z, et al. CD-HIT: accelerated for clustering the next-generation sequencing data[J]. Bioinformatics, 2012, 28(23): 3150-3152.

[13] TIAN Zheng, LI Xiaobin, JU Yanwei. Disturbing Analysis on Spectrum Clustering[J]. Science in China: Series E, 2007, 37(4): 527-543.

[14] JAIN A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666.

[15] DOMINGOS P. Prospects and challenges for multi-relational data mining[J]. ACM SIGKDD Explorations Newsletter, 2003, 5(1): 80-83.

Improved self supervised learning collection intelligence based high performance data clustering approach

ZENG Lingwei1, WU Zhenxing1, DU Wencai2

(1. College of Information and Electronic, Qiongzhou University, Sanya 572022 P.R. China;2. College of Information Science & Technology, Hainan University, Haikou 570228 P.R. china)

Abstract:For the problems that traditional data clustering approaches easily converge to local optima and the quality of the solution is not good, a high performance clustering approach which combines the improved self supervised learning collection intelligence and K-means is proposed. The existing self supervised learning approach has the advantage of computation efficiency and quality of clustering, but has the problem of low speed of convergence and trapping in local optimal easily. Firstly, a mutation mechanism is added to ISLCI that aims to reduce the probability of optima and the quality of optimal solution is improved; Secondly, the action function of each candidate is computed. Lastly, the object of the collection intelligence learning is selected by roulette approach, and the others in the population learn from the object to improve themselves. The converge speed is speeded up with K-means approach and the computation efficiency is improved. The compared experiment result demonstrated that the proposed approach has the characteristic of converge quickly, good quality of clustering solution and low probability to fall to local optima.

Keywords：self supervised learning collection intelligence; data clustering; mutation operation; intra-cluster distance; fitness function evaluation

DOI：10.3979/j.issn.1673-825X.2016.01.020

收稿日期：2014-12-10

修订日期：2015-10-09通讯作者：曾令伟sanyazenglingwei@126.com

基金项目：2014年海南省高等学校科学研究项目(HNKY2014-65)

Foundation Item：The Higher School Science Foundation Project of Hainan(HNKY2014-65)

中图分类号：TP181

文献标志码：A

文章编号：1673-825X(2016)01-0131-07

作者简介：

曾令伟(1978-)，男，湖南衡阳人，副教授，硕士，主要研究领域为数据挖掘，人工智能。E-mail：sanyazenglingwei@126.com。

伍振兴(1985-)，男，湖南娄底人，讲师,硕士，主要研究领域为软件工程，计算机网络。

杜文才(1953-)，男，江苏南通人，教授，博士，主要研究领域为海洋通信、计算机网络、物联网。

(编辑：张诚)