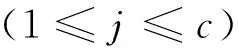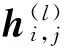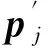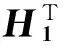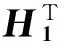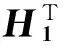一种改进的QC-LDPC码及其编码器FPGA实现

卫　霞,张文俊

(1．西北工业大学 明德学院 电子信息工程系，西安710124；2．陕西省通信管理局，西安710075)



一种改进的QC-LDPC码及其编码器FPGA实现

卫霞1,张文俊2

(1．西北工业大学 明德学院 电子信息工程系，西安710124；2．陕西省通信管理局，西安710075)

摘要：为了提高低密度准循环奇偶校验码(quasi-cyclic low density parity check codes, QC-LDPC)的编码码率灵活性和降低该码的实现复杂度，提出了一种改进的QC-LDPC码构造方法，并通过构造校验矩阵设计出了几种高码率码型，仿真结果表明该码在中、长帧长时性能优于相近参数的传统QC-LDPC码；针对该码型设计了一种基于随机存取存储器(random-access memory, RAM)的编码器硬件架构，通过存储地址指针实现对校验矩阵的存储，使得编码器能灵活地实现变码率和变帧长编码。采用verilog硬件描述语言在Spartan-3 XC3S1500芯片上实现了编码器。综合结果显示：新的硬件编码架构较基于移位寄存器的传统QC-LDPC码的编码器硬件架构，在编码延时保持相同而硬件资源大幅降低的情况下，编码器系统的最高频率达到了225.174 MHz，能满足高速编码需求。

关键词：低密度准循环奇偶校验码；基于RAM的编码器；变码率编码

0引言

低密度奇偶校验(low density parity check，LDPC)码[1]是一种性能逼近香农限的前向纠错编码技术。由于性能优异[2]、设计灵活、较低的译码复杂度[3]，LDPC码已被应用于多种通信标准之中[4]。但是，采用普通的编码方式，编码复杂度与码长平方成正比，使得码长较长时编码复杂度过高。

为了适应不同的信道环境，前向纠错编码的帧长及码率需要自适应调整以保证通信质量。因此，如何设计码率及帧长可以自适应调节的低复杂度的编译码器成为了当前编码领域研究的又一热点问题[5]。

YU Kou通过有限几何构造出的准循环LDPC码(quasi-cyclic LDPC, QC-LDPC)[6]，其编码器可以采用移位寄存器简单地实现，降低了编码复杂度，且性能在中短帧长时与对应参数的随机LDPC码相当。LIN Shu等人提出了由循环校验矩阵得出系统循环生成矩阵的方法，并基于此设计了几种基于移位寄存器的QC-LDPC高效编码器架构[7]。近两年，虽然KANG Jingyu 及DIAO Qiuju等学者对QC-LDPC码的构造方法进行了不同的改进[8-9]，但是其编码器架构依然需要基于移位寄存器实现。

2011年以来，Yau和Falcao等[10-11]分别采用图形处理器(graphics processing unit, GPU) 来测试LDPC 码性能，基于GPU的平台虽然不受移位寄存器架构限制，但是从工程应用方面考虑，基于GPU 的测试方案无助于工程应用。

工程实现时，移位寄存器对编码器码率及帧长自适应变化的灵活性造成了限制，同时文献[7]中的编码架构在硬件资源消耗上也存在优化空间。

为了克服现有QC-LDPC码编码器实现时的问题，本文作者提供了一种Mended QC-LDPC(MQC-LDPC)码。该结构可利用校验矩阵直接进行编码，并提供一种与该码结构对应的基于RAM实现的编码器，不仅有效降低硬件资源，还能实现灵活变码率编码。

1QC-LDPC码介绍

准循环LDPC码的校验矩阵Hqc具有(1)式形式。

(1)

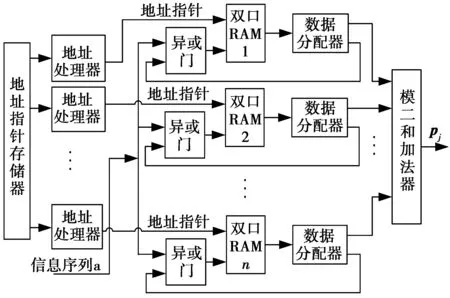
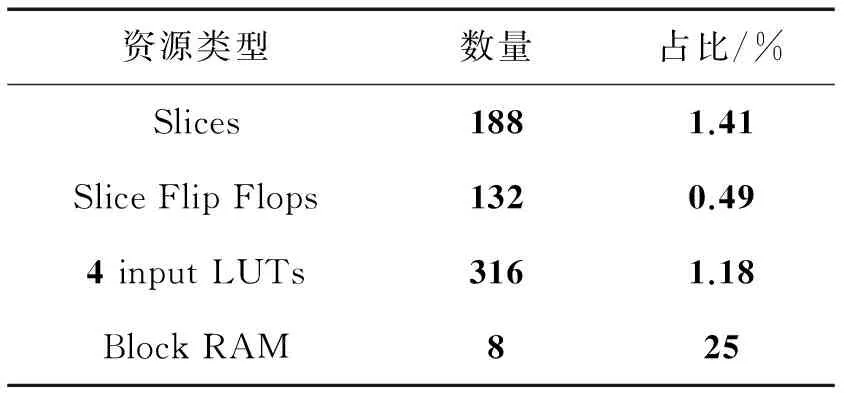
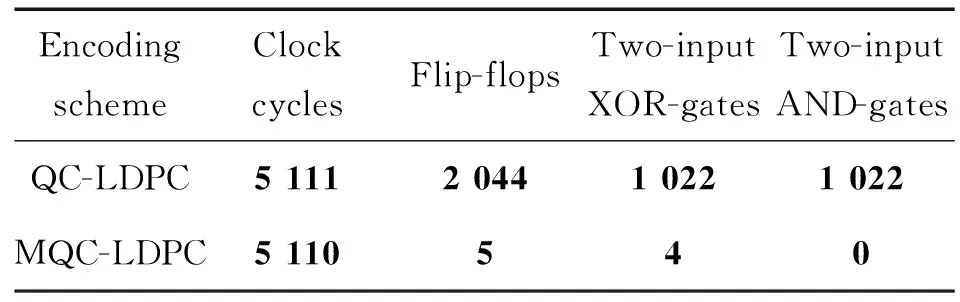
(1)式中：c,t为正整数，且c

①Ai,j的“重量”ω和b相比是个很小的整数，该条件保证了Hqc是稀疏矩阵；

②Ai,j组成的Hqc的任意两列(行)“1”的重叠度λ≤1，该条件保证了Hqc对应的二分图上长度是4的环不存在，进而保证了QC-LDPC码的译码性能[8]。

满足上述条件Hqc的“零空间”就构成了码长是b×t的QC-LDPC码。同时若Ai,j的“重量”都相同，那么其构成的Hqc对应的列重(行重)也相同，都等于ω×c(ω×t)，此时的QC-LDPC码即为“规则QC-LDPC”码，否则即为“非规则QC-LDPC”码。文献[9]提出了“系统-准循环生成矩阵”，即Hqc的秩与其行数相等且具有一个秩为r的c×c的子矩阵，此时Hqc对应的生成矩阵Gqc的结构为

(2)

(2)式中：0是b维的全零阵；I代表b维的单位矩阵；Gi,j代表b×b的循环方阵。

此时Gi,j可以被其第一行gi,j所确定，其中1≤i≤t-c,1≤j≤c，此时gi,j被称为Gi,j的“行生成矢量”。由此，相关文献在编码实现时把gi,j存储起来，通过移位寄存器来实现Gi,j，有效降低了存储资源，提升了编码效率[7]。但是在硬件实现时移位寄存器的长度不能灵活变动，进而限制了自适应编码的灵活性。而且由于Gi,j并非稀疏矩阵，在中长码型时，即使仅仅对其生成元存储也需要较多的存储器资源，所以QC-LDPC码依然存在优化空间。

2MQC-LDPC码构造及其性能分析

通过在QC-LDPC码的校验矩阵后面添加具有双对角形式的校验矩阵[12]，构造出MQC-LDPC码的校验矩阵，即H=[H1H2]，其中，H2如(3)式。

(3)

构造出参数为(6 131，5 110)的MQC-LDPC码，H的行重为22(第一行为21)，对应码率为0.83，校验矩阵H为

(4)

(4)式中，H1是一个1 021×4 088的矩阵，列重为4。则H的列重包括4，2和1 3种情况。同理，构造参数分别为(7 153，6 132)和(8 175，7 154)的MQC-LDPC码，对应码率分别为0.86和0.88，校验矩阵的行重分别为26(第1行为25)和30(第1行为29)。可见，3种码型的码率略有不同但均大于0.8，都属于高码率码型。

图1是上述3种参数的MQC-LDPC码和与其相近参数的QC-LDPC码的性能比较。由图1可见，MQC-LDPC码在帧长分别为6131，7153和8175比特时，其性能均比相近参数的QC-LDPC码略好。

3MQC-LDPC码编码器硬件实现

假定a为编码前输入的信息序列，C为编码后得到的码字，根据线性分组码的定义C=a·G，由MQC-LDPC的校验矩阵对应的生成矩阵具有系统形式：G=[I|P]，那么码字C就可以划分成信息序列a和校验序列p两部分，即C=[a|p]，获得校验序列p即可实现编码过程。已知校验矩阵H=[H1H2],且C·HT=0，因此

(5)

由此可推出校验序列为

(6)

(7)

图2　MQC-LDPC码编码器框架图Fig.2　Encoding structure of MQC-LDPC codes

图2中，中间校验序列pjk计算电路是在结合MQC-LDPC码的Hqc矩阵的整体特性以及H1矩阵的循环特性设计出的基于RAM的编码器架构，其中，引入双口RAM阵列存储中间校验比特，通过地址指针表征校验矩阵并指示双口RAM的操作地址，由对双口RAM的读写操作实现中间校验位的更新过程，最终将双口RAM阵列的中间校验比特进行模二加得到校验序列。中间校验序列pjk计算电路由异或门、地址指针存储器、地址处理器、双口RAM阵列、数据分配器以及模二加法器共6个部分组成，计算电路如图3所示。

图3　中间校验序列pj计算电路Fig.3　Intermediate check sequence pjcalculating circuit

(8)

(9)

表1　移位累加器电路操作真值表

实现时采用双口RAM，每个RAM每个时钟只能处理一个地址，所以为了提高编码速度，需要多个RAM同时操作，具体RAM的数目则与一列校验子矩阵中生成元中的1的个数相对应，每个RAM对应一组地址指针，当一帧信息位完成编码后，将所有RAM的相同位置的存储内容取出做模二和运算后送入重复累加器即得到了最终所求的中间校验序列。

3.2地址指针实现

地址指针处理器由2个双输入选择器以及模b加法器组成。双输入选择器中，第1个选择器的1个输入端固定接零，另1个输入端固定接1；第2个选择器的1个输入端接地址指针存储器的输出端，另1个输入端接加法器的输出端。地址指针处理器每b个时钟读取一次地址指针存储器的值，且仅在当前时钟时第1个选择器选择0作为输入，其余b-1个时钟选择器选择1作为输出，这样就实现了对RAM操作的地址指示。

3.3变码率实现

同理，对于(8 175，7 154)码，其校验矩阵形式为

(10)

4编码器性能分析

传统的QC-LDPC码在编码时，充分利用码字特点，首先将校验矩阵通过计算变换成生成矩阵，然后利用生成矩阵的循环特性，通过移位寄存器进行编码。而本文基于RAM的MQC-LDPC码编码架构，直接利用校验矩阵的特点，不需要求出生成矩阵而直接利用校验矩阵进行编码，由于校验矩阵的稀疏循环特性，从而使得编码器占用的硬件资源与传统的编码器相比大幅度降低；由于引入了地址指针表示校验矩阵的存储，不仅大大降低了存储校验矩阵的资源，而且可以灵活实现变码率编码。

在ISE 6下使用Verilog HDL语言采用Xilinx公司的Spartan-3 XC3S1500芯片，设计了参数为(6 131，5 110)和(8 175，7 154)MQC-LDPC码的编码器，资源占用情况如表2所示，最终综合结果表明整个编码器系统的最高频率为225.174 MHz。由于编码器主要模块有效地实现了复用，所以实现更多码率时，除了Block RAM资源，其他资源类型不会额外增加。

表2　(6131，5110)和(8175，7154)MQC-LDPC码编码器

(11)

(11)式中，Ai,j的维数b=511。转换成对应的生成矩阵，需要存储6×2×511=6 132个二进制数值。表3给出了实现相同参数的2种码型所需要资源对比情况。如上所述，同QC-LDPC码编码器实现时所用的移位寄存器以及存储器相比，资源占用率大为降低。

表3　QC-LDPC码编码实现和MQC-LDPC

综上所述，基于RAM实现的MQC-LDPC码的编码器较之与基于移位寄存器实现的QC-LDPC码编码器在编码保持相同的情况下，在硬件资源占用上有了大幅的降低。

5结论

本文提出了一种对QC-LDPC的改进构造，该结构在中、长帧长时编码性能较之于QC-LDPC码有所提升，该改进码型具有线性的编码复杂度。本文还针对该改进码型提出了基于RAM的硬件实现架构。与传统的利用移位寄存器实现QC-LDPC码的编码器相比，该架构不仅在硬件资源占用上大为降低，而且由于对校验矩阵的存储简化为对地址指针的存储，更加有利于灵活变码率实现。这就为LDPC码在不同通信质量和传输环境下的应用提供了可能性。

参考文献：

[1]GALLAGER R G. Low-Density Parity-Check Codes[D]. IRE Transactions Information Theory. 1962 (8):21-28.

[2]MACKAY D J C, NEAL R M. Near Shannon Limit Performance of Low-Density Parity-Check Codes[J]. Electronics letters. 1997 (33):457-458.

[3]DARABIHA A, CARUSONE A C, KSCHISCHANG F R. Multi-Gbit/sec Low Density Parity Check Decoders with Reduced Interconnect Complexity[EB/OL]. [2015-01-12]. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1465805, 2005-08-25/2008-07-10.

[4]XU Dazheng, LIU Aijun. Research on Combined LDPC Decoding Iterative Soft—Decision Demodulation Algorithm of 16·APSK in DVB-S2[J]. Journal of Astronautics, March, 2011, 94 (1):634-639.

[5]SUN Y, KARKOOTI M, CAVALLARO J R. VLSI decoder architecture for high throughput, variable block-size and multi-rate LDPC codes[C]// IEEE International Symposium on Circuits and Systems, 2007. New Orleans, LA : IEEE, 2007: 2104-2107.

[6]YU Kou, LIN Shu, FOSSORIER M P C. Low-density parity-check codes based on finite geometries: a rediscovery and new results[J]. IEEE Trans Info Theory, 2001, 47 (7)：2711-2736.

[7]LI Zongwang, CHEN Lei, ZENG Lingqi, et al. Efficient Encoding of Quasi-cyclic Low-Density Parity-Check Codes[J]. IEEE Transactions on Communications, 2006, 54(1):71-81.

[8]KANG Jingyu, HUANG Qin, ZHANG Li, et al. Quasi-Cyclic LDPC Codes: An Algebraic Construction[J]. IEEE Transactions on Communications, 2010, 58(5): 1383-1396.

[9]DIAO Qiuju, HUANG Qin, LIN Shu. Life Fellow, IEEE, and Khaled Abdel-Ghaffar. A Matrix-Theoretic Approach for Analyzing Quasi-Cyclic Low-Density Parity-Check Codes[J]. IEEE Transactions on Information Theory, 2012, 58(6): 4030-4048.

[10] YAU S F, WONG T L, LAU F C M. Extremely fast simulator for decoding LDPC codes[C]//Proceeding of 13th International Conference on Advanced Communication Technology(ICACT). Gangwon-Do, Korea:IEEE, 2011: 635-639.

[11] FALCAO G, ANDRADE J, SILVA V, SOUSA L. GPU-based DVB-S2 LDPC decoder with high throughput and fast error floor detection[J]. Electronics Letters, 2011, 47(9):542-546.

[12] CAI Z, HAO J, TAN P H, et al. Efficient encoding of IEEE 802.11n LDPC codes[J]. Electronics Letters, 2006, 42(25): 1471-1472.

[13] YANG M, RYAN W E,YAN L. Design of Efficiently Encodable Moderate-Length High-Rate Irregular LDPC Codes[J]. IEEE Transactions on Communications, 2004, 52 (4): 564-571.

An improved structure of QC-LDPC codes and its FPGA encoder implementation

WEI Xia1，ZHANG Wenjun2

(1. Department of Electronic Information Engineering, Mingde College of Northwestern Polytechnical University, Xian 710124, P. R. China;2. Shanxi Communications Administration, Xian 710075, P. R. China)

Abstract:In order to increase encoding rate flexibility and reduce its operation complexity, an improved structure of QC-LDPC codes is proposed, and several high rate codes were designed. Simulation result shows that the performance of the improved LDPC codes is better than that of conventional QC-LDPC codes in moderate and long frame length. An encoding architecture based on RAM is designed. The encoder stores the check matrix by storing address-pointers, thus multi-rate encoding is flexible. The encoder is implemented with Verilog HDL language on the chip of Spartan 3 XC3S1500. Synthesis reports show that the systems maximum frequency is 225.174 MHz with less resource and the same encoding time-delay of normal QC-LDPC encoder based on shift-register.

Keywords：quasi-cyclic low density parity check codes; encoder based on RAM; multi-rate encoding

DOI：10.3979/j.issn.1673-825X.2016.01.009

收稿日期：2015-03-18

修订日期：2016-01-05通讯作者： 张文俊185691479@qq.com

中图分类号：TN911.22

文献标志码：A

文章编号：1673-825X(2016)01-0060-06

作者简介：

卫霞(1984-)，女，山西运城人，讲师，硕士，主要从事信道编码方面的研究。

E-mail：wxia66@163.com。

张文俊(1984-)，男，河南商丘人，工程师，硕士，工作研究方向为信道编码、网络与信息安全。E-mail：185691479@qq.com。

(编辑：魏琴芳)