伺服增益不匹配的双轴同步误差补偿策略

陈　琳　程正波　黄炳琼　潘海鸿

1.广西大学，南宁，5300042.广西制造系统与先进制造技术重点实验室，南宁，530004

伺服增益不匹配的双轴同步误差补偿策略

陈琳1,2程正波1黄炳琼1,2潘海鸿1,2

1.广西大学，南宁，5300042.广西制造系统与先进制造技术重点实验室，南宁，530004

摘要：针对双轴驱动系统中由两轴伺服增益不匹配造成的运动不同步问题，从单轴稳态误差分析入手，构建单轴跟踪误差与两轴同步误差的关系。推导出参考位置为斜坡信号时同步误差的理论计算公式，确定两轴伺服增益系数及进给速度与同步误差间的定量关系；基于推导所得公式，提出将速度影响因子引入交叉耦合控制器中，并给出两种同步误差补偿策略(策略1和策略2)。通过仿真与实验验证了所推导同步误差理论计算公式的正确性；所提出的两种同步误差补偿策略均能有效减小因两轴伺服增益系数不匹配而产生的同步误差，且补偿后单轴系统的动态响应性能不会受到影响；与采用补偿策略1相比，采用补偿策略2后所获得的同步误差曲线更为平稳。

关键词：双轴驱动系统；伺服增益不匹配；同步误差；误差分析；交叉耦合控制

0引言

双轴同步驱动结构可使系统获得高的加速度特性，并可拓展系统带宽，被广泛应用于高速、高精度数控机床等工业领域[1]，但由于受机械耦合、外部扰动以及两轴伺服增益不匹配等因素的影响，轴间运动会不协调而产生同步误差[2-4]，进而影响机床的轮廓加工精度。因此，分析双轴驱动系统动态同步误差的形成机理、设计高性能的同步误差补偿控制器对双轴同步驱动结构的推广应用具有重要意义。

为解决双轴驱动系统的同步运动问题，文献[4]对龙门双轴驱动系统中的机械耦合进行解耦，并提出一种前馈与反馈相结合的解耦控制器，使系统同步运动性能得到提高。文献[5]采用PID控制算法，设计动态同步误差补偿控制器，通过实验验证了该控制器的有效性。文献[6]提出一种PD交叉耦合控制器，以抑制外部扰动对同步运动性能的影响，该控制器在提高运动同步性能的同时不影响整个系统的跟踪带宽。文献[7]提出一种基于构建伺服机构动力学模型的多变量辨识方法，基于辨识得到的模型设计同步控制器，以减少双轴同步运动中的位置和速度同步误差。文献[8]对龙门系统中的机械耦合进行分析，提出一种基于推力分配的同步控制策略，结合自适应鲁棒控制算法使龙门双轴系统的同步性和协调性均得到提高。文献[9]将模型参考自适应控制与变结构控制相结合，以提高双轴驱动系统的同步运动精度。文献[10]通过设计最优预见前馈补偿与基于模糊控制的交叉耦合补偿控制器，使龙门移动式数控机床在不平衡负载扰动下仍具有良好的同步性能。

以上研究主要是针对机械耦合与外部扰动因素提出相应的同步控制策略，而对于由两轴伺服增益系数不匹配引起的运动不同步问题，目前研究较少。在实际控制系统中，可通过调整位置控制器增益系数调节单轴伺服增益系数，但要将两轴伺服增益系数调节到完全相等非常困难。为此，以双轴驱动系统中由两轴伺服增益不匹配引起的同步误差为研究对象，分析双轴驱动系统产生同步误差的机理，并结合交叉耦合控制思想，设计同步误差补偿策略。最后，通过仿真和实验验证了所提出的同步控制策略的有效性。

1同步误差产生分析

本文采用同步主端控制方式[7]进行双轴同步驱动控制。为便于分析，将由伺服驱动器、伺服电机等组成的被控对象模型简化为一阶惯性环节[11]，位置控制器采用比例控制，其控制系统框图见图1，R为轨迹发生器产生的参考位置指令，e1、e2为两轴位置跟踪误差，Kp1、Kp2为两轴位置控制器比例增益，u1、u2为运动控制器输出的两轴控制命令，d1、d2为两轴负载扰动，Kv1、Kv2为两轴被控对象模型增益系数，τv1、τv2为两轴被控对象模型积分时间常数，v1、v2为两轴实际进给速度，x1、x2为两轴实际位移。

图1　双轴同步驱动控制系统框图

在不考虑机械耦合及负载扰动的情况下，当参考位置为斜坡信号时，系统稳态跟踪误差为[12]

(1)

Ki= KpiKvi

式中，v为参考进给速度；Ki为系统伺服增益系数。

由于两轴同步驱动过程中参考位置指令相等，故两轴同步驱动过程中所产生的位置同步误差可表示为

esyn(t)=x1(t)-x2(t)=

(2)

由式(2)可知，当参考位置为斜坡信号且稳态运行时，若K1=K2，则esyn(t)=0；若K1≠K2，则esyn(t)与v成正比关系。即两轴伺服增益系数不匹配将导致同步误差产生，且同步误差大小与设定的进给速度相关。

2同步误差补偿控制器设计

为提高双轴驱动系统在两轴伺服增益系数不匹配时的同步运动性能，并抑制同步误差随进给速度变化而变化的特性，将速度因子引入到同步误差补偿控制器中，设计两种同步误差补偿策略。

同步误差补偿策略1采用两轴实际进给速度的平均值与补偿系数Kpc1相乘，作为速度变化的自适应因子，再与实际检测到的位置同步误差相乘，获得两轴位置同步误差补偿量，并输出到位置控制器之前，以修正参考位置信息。补偿策略如下：

(3)

式中，c1(t)、c2(t)为两轴t时刻的位置同步误差补偿值；Kpc1为控制器补偿系数。

由式(3)并结合交叉耦合控制思想[13]设计同步误差补偿策略1控制器，其结构如图2a所示。

同步误差补偿策略2在同步误差补偿策略1的基础上添加速度同步误差补偿项，将实际检测到的位置同步误差进行微分得到速度同步误差，与补偿系数Kdc2相乘后获得速度同步误差补偿量，并输出到位置控制器之后，以修正速度控制量。补偿策略如下：

(4)

式中，cp1(t)、cp2(t)为两轴t时刻的位置同步误差补偿值；cv1(t)、cv2(t)为两轴t时刻的速度同步误差补偿值；Kpc2、Kdc2为控制器补偿系数。

由式(4)并结合交叉耦合控制思想[13]设计同步误差补偿策略2控制器，其结构如图2b所示。

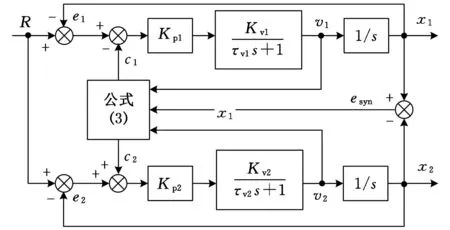
(a)同步误差补偿策略1

(b)同步误差补偿策略2图2　交叉耦合同步误差补偿控制器结构图

3仿真与实验验证

为验证所推导的双轴运动系统同步误差产生机理的正确性，以及所提出的同步误差补偿策略的有效性，搭建了图3所示的实验平台，该平台主要包括基于DSP+FPGA架构的运动控制板卡、伺服驱动器及控制电路和交流永磁同步电机(PMSM，型号SGMPH-01A1A21)。实验时PMSM驱动器的编码器信号配置为增量式输出(即线数为16 384)，并在运动控制板卡中对编码器信号进行4倍频处理；假设与电机连接的滚珠丝杠导程为5 mm，则系统位置分辨率可达0.1 μm。

利用MATLAB软件自带系统辨识工具箱进行系统辨识[14]，分别获得两轴被控对象的一阶模型如下：

(5)

系统辨识所需的输入信号为控制板卡输出的参考角度值，所需的输出信号为折算后滚珠丝杠平台的运行速度。

图3　实验平台实物图

3.1同步误差产生分析结果验证

为验证参考位置为斜坡信号时同步误差产生机理的正确性，结合辨识所得被控对象模型，建立图4所示仿真模型。取参考速度v=10 mm/s，两轴位置控制器增益系数分别为Kp1=0.012、Kp2=0.010，对运动过程中产生的同步误差进行理论计算、模型仿真和实际平台检测，对比曲线如图5所示。

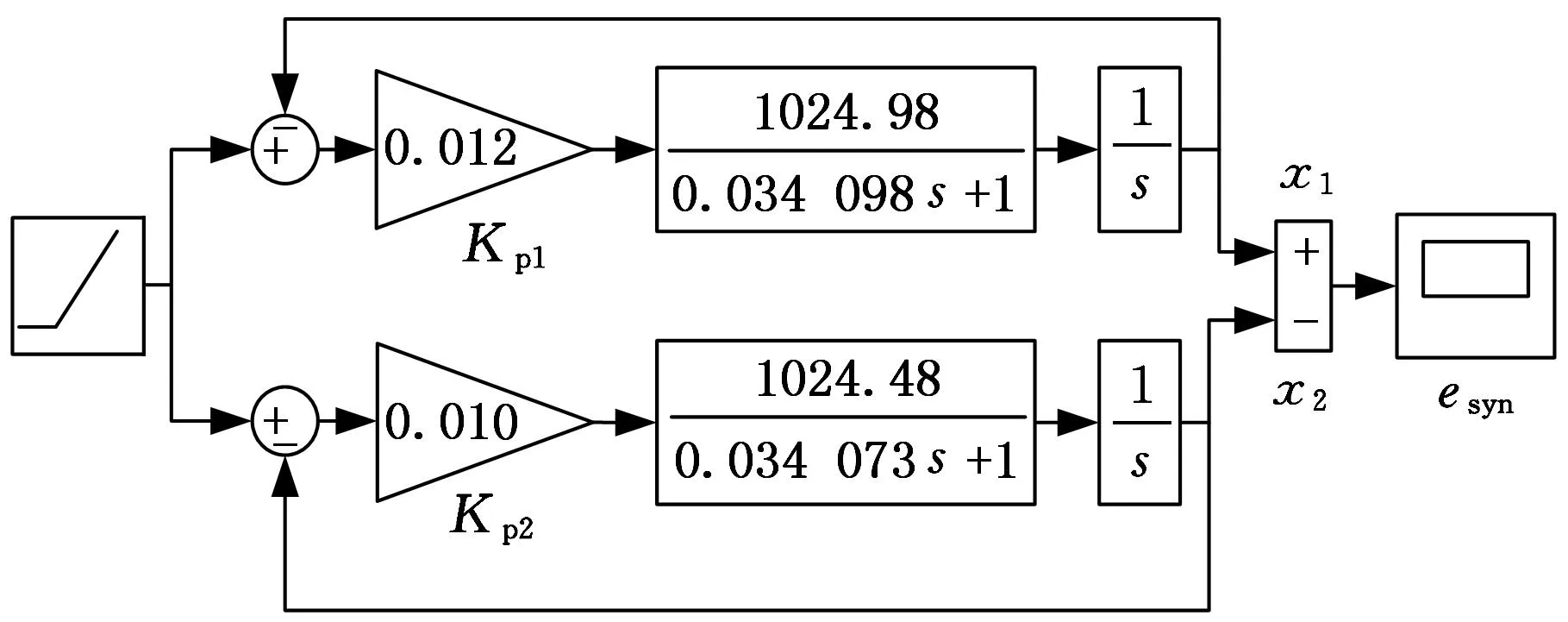
图4　双轴同步运动系统仿真模型

图5　参考位置为斜坡信号时同步误差对比曲线

由图5可知，在0～0.5 s时间域内，由于理论计算公式忽略时域响应瞬态部分的影响，理论计算结果与仿真和实验结果有一定偏差，但仿真结果与实验测量结果具有相同的变化趋势，且数值相近。在0.5 s以后，三种方式获得的同步误差曲线变化趋于稳定，理论计算所得同步误差与仿真获得同步误差相等；实验检测得到的同步误差由于外部扰动及测量噪声的存在，其数值存在波动。0.5～2 s内实验检测所得同步误差数据的平均值为166.63 μm，标准差为5.95 μm，与理论计算和仿真模型获得结果163.08 μm相近。因此可以得出结论：同步误差理论计算公式(式(2))正确，可以准确描述参考位置为斜坡信号时产生的同步误差。

3.2同步误差补偿策略实验验证

结合辨识所得被控对象模型，通过Simulink仿真和实际平台实验分别进行参考位置为正弦信号和斜坡信号的同步误差补偿实验。取两轴位置控制器增益系数Kp1=0.012、Kp2=0.010，同步误差补偿策略1的补偿系数Kpc1=350，同步误差补偿策略2的补偿系数Kpc2=350、Kdc2=0.05。采用S形加减速控制方式，加速度为250 mm/s2、加加速度为20 000 mm/s3。参考位置为正弦信号时，分别取速度幅值v为10，50，100 mm/s进行同步误差补偿实验；参考位置为斜坡信号时，分别取进给速度v为10，50，100 mm/s进行同步误差补偿实验。补偿前、采用补偿策略1与采用补偿策略2的实验结果见图6～图9，其中数据采样周期为10 ms。

1.v=10 mm/s　2.v=50 mm/s　3.v=100 mm/s(a)补偿前

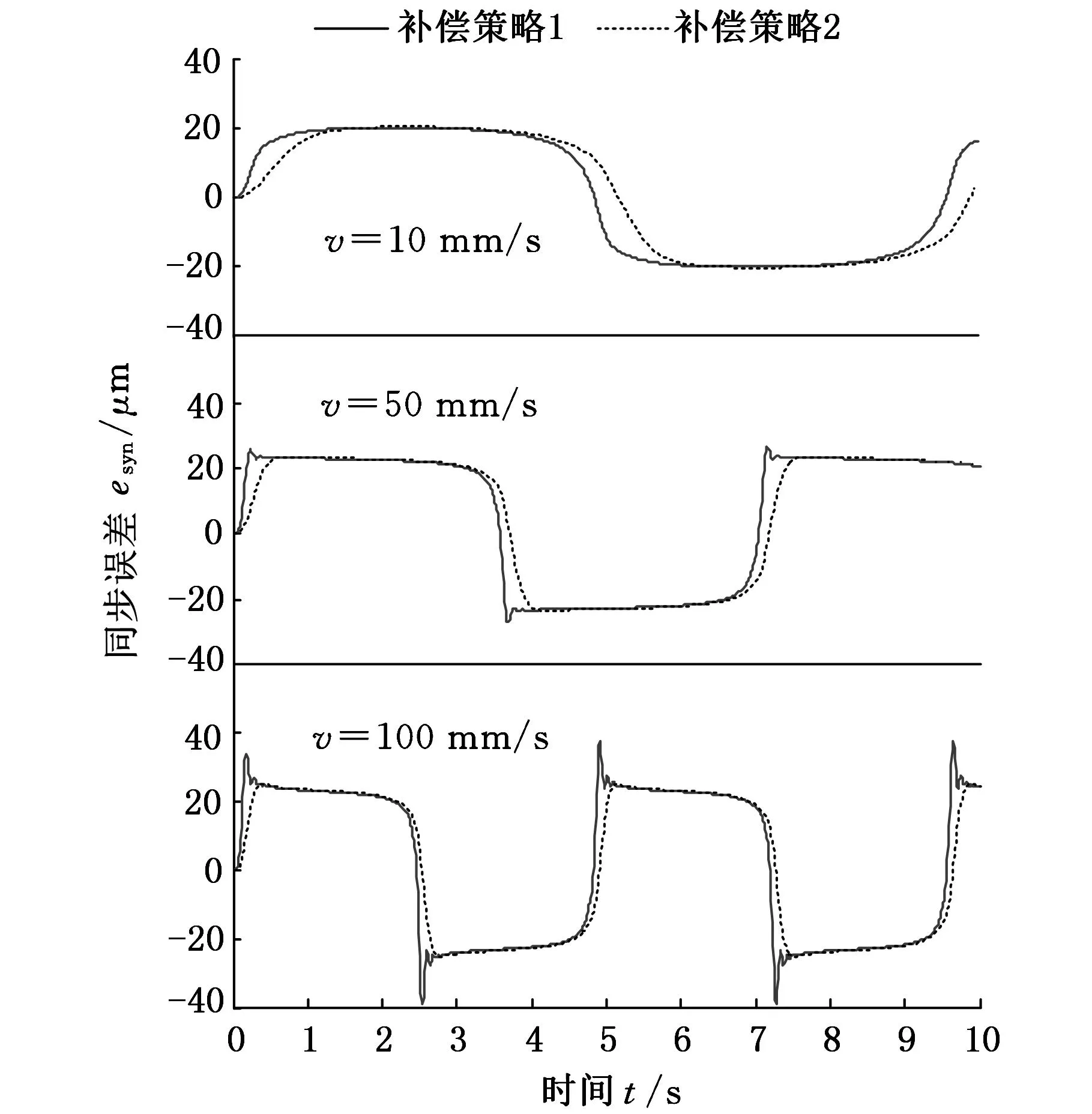
(b)补偿后图6　参考位置为正弦信号时各进给速度的仿真结果

由图6～图9可知，仿真与实验所获得的同步误差曲线变化规律相同。当输入参考位置分别为正弦信号和斜坡信号时，未补偿情况下同步误差峰峰值随进给速度的增大而增大；采用所提出的两种同步误差补偿策略后，同步误差峰值随进给速度增大而增大的特性得到抑制。比较两种补偿策略获得的同步误差曲线可知，补偿策略2所得误差曲线数据波动较小。表1所示为两种位置参考信号下的同步误差实验数据分析结果，其中同步误差峰值为1～2 s间实验数据的平均值。

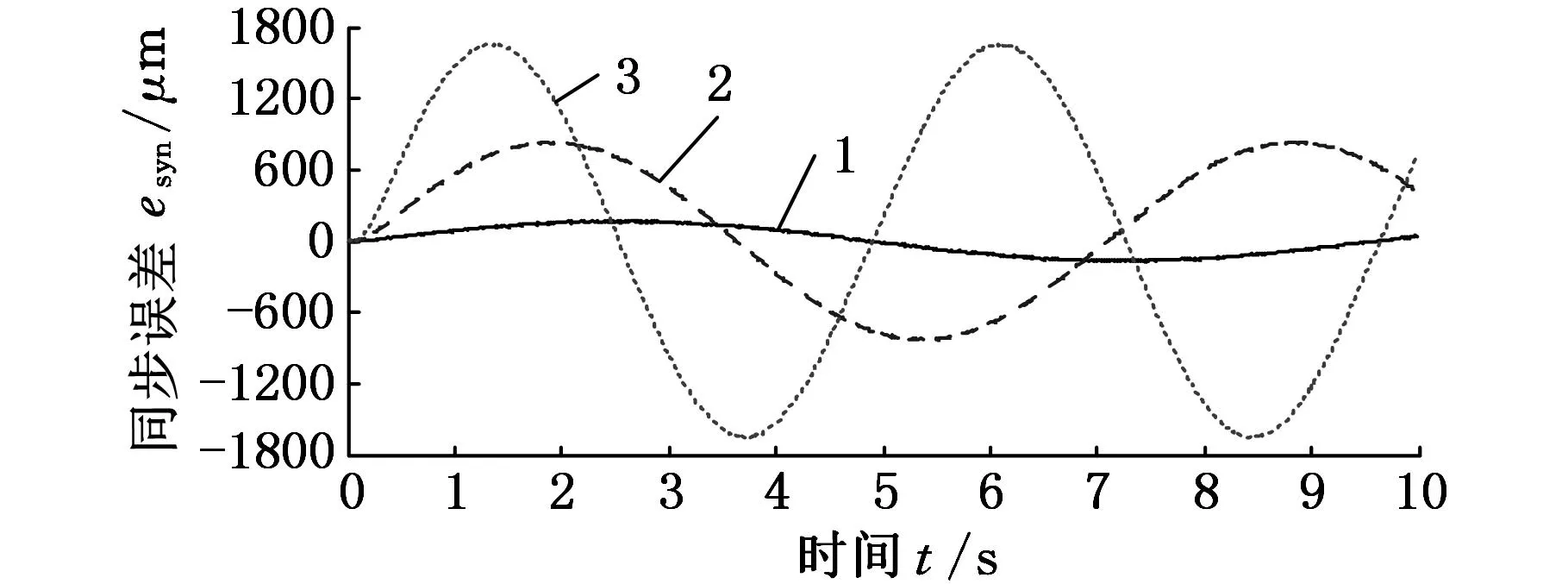
1.v=10 mm/s　2.v=50 mm/s　3.v=100 mm/s(a)补偿前

(b)补偿后图7　参考位置为正弦信号时各进给速度的实验结果

1.v=10 mm/s　2.v=50 mm/s　3.v=100 mm/s(a)补偿前

(b)补偿后图8　参考位置为斜坡信号时各进给速度的仿真结果

1.v=10 mm/s　2.v=50 mm/s　3.v=100 mm/s(a)补偿前

(b)补偿后图9　参考位置为斜坡信号时各进给速度的实验结果

同步误差补偿策略参考位置信号类型进给速度(mm/s)同步误差峰值(μm)同步误差减小百分比(%)未补偿正弦信号斜坡信号10174.6450837.781001659.4710166.6650833.291001666.42补偿策略1正弦信号斜坡信号1020.3988.325023.2997.2210023.1098.611020.8487.505023.3597.2010023.4898.59补偿策略2正弦信号斜坡信号1020.0188.545022.8197.2810022.9898.621020.9287.455023.1697.2210023.5198.59

由表1可知，不管参考位置为正弦信号还是斜坡信号，采用所提出的同步误差补偿策略后，三种进给速度下的同步误差幅值均稳定在22 μm附近。当进给速度为10 mm/s时，所提出的两种补偿策略均能将同步误差减小88%左右；当进给速度为50 mm/s时，所提出的两种补偿策略均能将同步误差减小97%以上；当进给速度为100 mm/s时，所提出的两种补偿策略均能将同步误差减小98%以上。

为探讨所提出的两种同步误差补偿策略对系统动态响应性能的影响，当参考位置为斜坡信号时，以进给速度v=50 mm/s为例，分析x1输出轴在补偿前、采用补偿策略1与采用补偿策略2情况下的速度响应曲线，如图10所示。

(a)完整速度响应曲线

(b)0.25～0.55 s速度响应曲线放大图

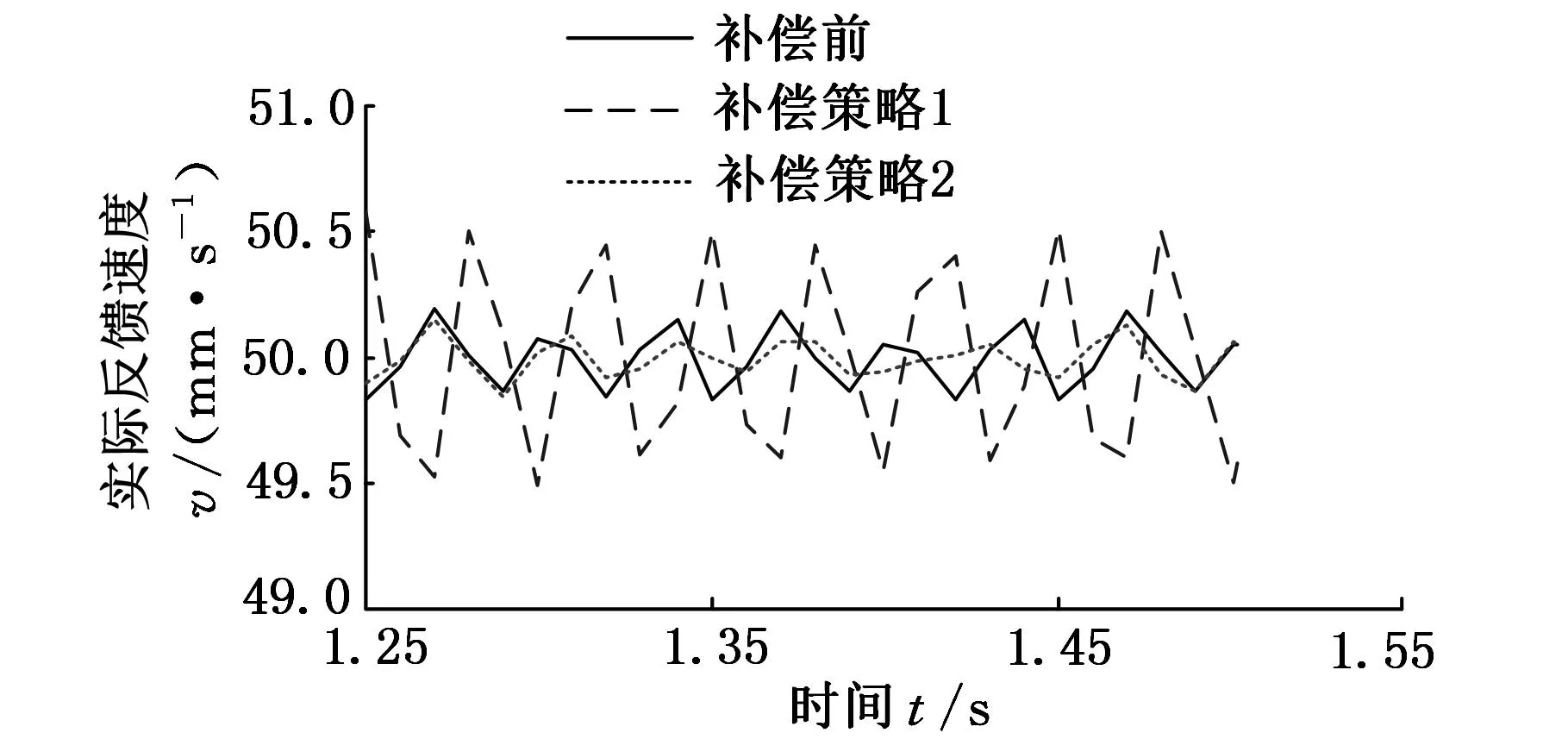
(c)1.25～1.55 s速度响应曲线放大图图10　参考位置为斜坡信号且进给速度v=50 mm/s时，补偿前与补偿后的速度响应曲线

由图10可知，所提出的两种补偿策略对系统的动态响应性能没有明显影响。在匀速运行阶段，采用补偿策略2所获得的速度曲线与补偿前基本保持一致，而采用补偿策略1则会使速度波动变大。由以上分析可知，当两轴伺服增益系数不匹配时，所提出的两种同步误差补偿策略均能有效减小系统运行过程中产生的同步误差，且补偿后的同步误差不会随进给速度增大而增大。但采用补偿策略2获得的误差曲线波动较小，且速度运行平稳。因此，与同步误差补偿策略1相比，同步误差补偿策略2具有更好的补偿性能。

4结语

对由两轴伺服增益系数不匹配引起的运动不同步问题进行研究，分析得出参考位置为斜坡信号时两轴伺服增益系数及进给速度与同步误差间的定量关系表达式；基于分析所得同步误差关系式，提出两种基于交叉耦合控制思想的同步误差补偿策略。通过仿真和实验分析可知：①同步误差理论计算结果能准确描述参考位置为斜坡信号时产生的同步误差；②设计的两种同步误差补偿策略在给定位置命令及进给速度下均能有效减小同步误差，补偿后的同步误差峰值在各进给速度下基本保持不变，且补偿策略2所得同步误差曲线更为稳定；③在系统中加入所提出的两种补偿策略均不会影响系统的响应性能。

所提出的两种补偿策略均能使系统在两轴伺服增益系数不匹配时仍具有良好的同步性能。因此，在调节两轴伺服参数时允许两轴伺服增益系数存在一定的差异，可缩短调整两轴伺服参数所需时间。

参考文献：

[1]李玉霞,赵万华,程瑶,等.动梁式龙门机床的双驱同步控制系统建模[J].西安交通大学学报,2012,46(4):119-124.

Li Yuxia, Zhao Wanhua, Cheng Yao, et al. Synchronous Control System Modeling of Gantry-Type Machine Tools[J]. Journal of Xi’an Jiaotong University, 2012,46(4):119-124.

[2]Ramesh R, Mannan M A, Poo A N. Tracking and Contour Error Control in CNC Servo Systems[J]. International Journal of Machine Tools & Manufacture, 2005, 45(3):301-326.

[3]郭庆鼎, 蓝益鹏. 双直线电机驱动的龙门移动式加工中心H∞鲁棒自适应控制[J]. 中国机械工程, 2003, 14(22):1966-1969.

Guo Qingding, Lan Yipeng. H∞Robust Adaptive Control for Double Linear Motor Drive of Gantry Moving Type Machining Centers[J]. China Mechanical Engineering, 2003, 14(22):1966-1969.

[4]García-Herreros I, Kestelyn X, Gomand J, et al. Model-based Decoupling Control Method for Dual-drive Gantry Stages: a Case Study with Experimental Validations[J]. Control Engineering Practice, 2013, 21(3): 298-307.

[5]程瑶, 赵万华, 李玉霞,等. 动梁式龙门机床双驱动态不同步误差补偿研究[J]. 中国机械工程, 2012, 23(8):915-919.

Cheng Yao, Zhao Wanhua, Li Yuxia, et al. Research on Compensation of Dynamic Non-synchronous Errors of Dual-drive System in Gantry-type Machine Tools[J]. China Mechanical Engineering, 2012, 23(8):915-919.

[6]Kosuke I, Burak S, Eiji S. Cross Coupling Controller for Accurate Motion Synchronization of Dual Servo Systems[J]. International Journal of Automation Technology, 2013, 7(5):514-522.

[7]Yao W S, Yang F Y, Tsai M C. Modeling and Control of Twin Parallel-axis Linear Servo Mechanisms for High-speed Machine Tools[J]. International Journal of Automation and Smart Technology, 2011, 1(1): 77-85.[8]Li C, Yao B, Zhu X, et al.Adaptive Robust Synchronous Control with Dynamic Thrust Allocation of Dual Drive Gantry Stage[C]//2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM).New York: IEEE, 2014:316 - 321.[9]Wang S M, Wang R J, Tsooj S. A New Synchronouserror Control Method for CNC Machine Tools with Dual-driving Systems[J]. International Journal of Precision Engineering & Manufacturing, 2013, 14(8):1415-1419.

[10]王丽梅, 唐雅萍. 龙门移动式数控机床的模糊交叉耦合补偿控制[J]. 机床与液压, 2010, 38(3):14-17.

Wang Limei, Tang Yaping. Fuzzy Cross-coupling Compensation Control for Gantry-moving Type CNC Machine Tool[J]. Machine Tool & Hydraulics, 2010, 38(3):14-17.

[11]Byun J H, Choi M S. A Method of Synchronous Control System for Dual Parallel Motion Stages[J]. International Journal of Precision Engineering and Manufacturing, 2012, 13(6): 883-889.

[12]董景新,赵长德,郭美凤,等. 控制工程基础[M]. 3版. 北京：清华大学出版社，2009.

[13]Koren Y. Cross-coupled Biaxial Computer Control for Manufacturing Systems[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4): 265-272.

[14]李鹏波,胡德文,张纪阳,等. 系统辨识[M]. 北京：中国水利水电出版社，2010．

(编辑王艳丽)

Synchronization Error Compensation Strategies in Dual-drive System for Servo Gain Mismatch

Chen Lin1,2Cheng Zhengbo1Huang Bingqiong1,2Pan Haihong1,2

1.Guangxi University,Nanning,530004 2.Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology,Nanning,530004

Abstract:The mismatch of dual-axis servo gain parameters might bring negative impacts on the issues of synchronization in dual-drive system. To solve this problem, the relationship among tracking errors from single axis and the synchronization errors from dual-axis was investigated, by analysis of steady-state-error from single axis. Then the analytic formula of the synchronization errors was derived as reference position of ramp type applied. And then the quantitative relationship among the synchronization errors and parameters (the dual servo gain and feed rate) was built and determined.Furthermore, two novel compensation strategies for compensating synchronization errors were raised by introducing velocity factor into cross-coupling controller. Experimental and simulation results were given to verify the validity of the proposed scheme for obtaining synchronization errors. It can also be proved that both of two strategies can suppress synchronization errors effectively, which is caused by dual-axis servo gain mismatch. And the dynamic responses of single axis system is not affected after the proposed control strategies applied. By comparison of the two compensation strategies, smoother curve of synchronization errors may be obtained using the second compensation strategy.

Key words:dual-drive system; servo gain mismatch; synchronization error; error analysis; cross-coupling control

收稿日期：2015-07-27

基金项目：国家自然科学基金资助项目(51465005)；广西制造系统与先进制造技术重点实验室项目(13-051-09S05,14-045-15S09)；广西教育厅资助项目(ZL2014002,ZL2014003)

中图分类号：TP273

DOI：10.3969/j.issn.1004-132X.2016.11.016

作者简介：陈琳，女，1973年生。广西大学机械工程学院教授。主要研究方向为数控技术、数字信号检测与处理、伺服电机控制。发表论文40余篇。程正波，男，1990年生。广西大学机械工程学硕士研究生。黄炳琼，女，1965年生。广西大学机械工程学院高级实验师。潘海鸿(通信作者)，男，1966年生。广西大学机械工程学院教授、博士研究生导师。