利用Eviews8.0预测中国GDP的增长
王子惠


摘 要 GDP作为一个国家一定时期内所生产和提供的最终商品和劳务的总和的重要指标,如果能够做出模型对其进行正确的预测,就可以有效地引导经济的发展,为决策提供依据。本文依据1952~2015年我国GDP的数据,建立了ARMA模型,并利用Eviews8.0统计软件实现对模型的检验。结果显示,模型具有较好的预测结果和现实意义。
关键词 GDP预测 ADF单位根检验 时间序列分析
一、引言
社会经济活动千变万化,许多经济现象都具有随着时间而演变的特点,描述数据与时间存在密切的联系。要想认识这些社会经济现象的本质特征,就需要研究这些现象随时间变化的规律,也就是需要进行动态分析。在对社会经济活动的分析中,时间序列数据是最常见的数据之一,是将观测到的数据按照时间的先后顺序排列起来所得到的,利用Eviews软件可以对经济现象做一个有效的预测和评估。
二、模型的建立
(一)数据来源及说明
本文研究的样本区间设定为1952~
2015年,数据来源于中国经济网和国家统计局官网数据库。为了能更好地观测数据的趋势,分别绘制该段时期中国GDP的原始统计数据、一阶差分数据、二阶差分数据,可以看出二阶差分数据大致是平稳的。
(二)通过ADF检验判断各个数据的平稳性
本文选用ADF(augmented Dickey-Fuller Test)检验,我们可以看出中国1952~2015年GDP的上升趋势很明显,因此对其进行一阶差分和二阶差分,得到二阶差分。对原始数据进行ADF检验,检验结果显示,GDP序列的伴随概率为1,即认为以100%的概率接受原假设,也就是存在单位根,数据不平稳。将GDP进行一阶差分后,继续ADF检验。检验结果显示,GDP序列的伴随概率仍然为1,同样认为一阶差分后的数据以100%的概率接受原假设,存在单位根,一阶差分后的数据仍不平稳。再对GDP进行二阶差分,然后ADF检验,此时选择不含趋势项和截距项。检验结果显示,二阶差分序列DDGDP在5%的显著性水平下拒绝原假设,接受不存在单位根的结论,同时认为二阶差分后的数据是平稳的。因此可以确定GDP序列是2阶单整序列,即GDP~Ⅰ(2)。[1]
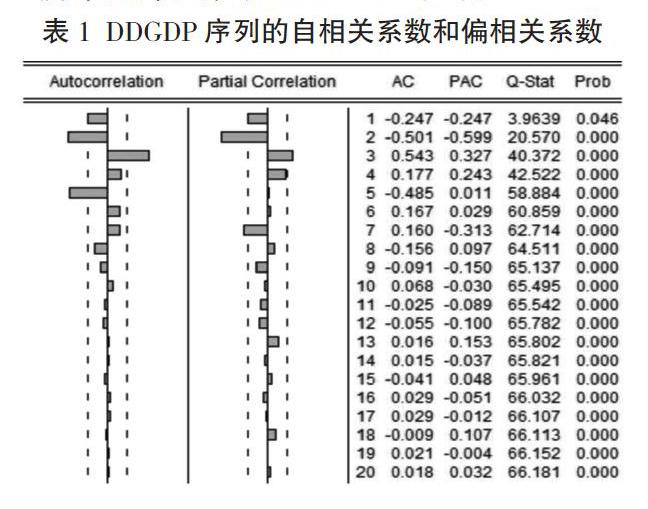
(三)模型的识别和选择
通过二阶差分数据的自相关系数(AC)和偏相关系数(PAC)并进行比较,见表2。建立关于ddgdp、ar(2)、ar(3)的模型,得到表3,从表3中可以看出AR(2)和AR(3)系数的伴随概率P均为0,小于0.05。因此认为通过显著性检验,同时拟合优度R-squared为0.63,拟合较好。接下来就是进行模型残差的相关性检验,Q统计量的P值基本上都大于0.05,因此认为接受原假设,通过检验,残差不存在相关性,系数显著为0,是白噪声序列,因此认定该模型成立。建立的模型为:DDY=
-0.5611*AR(2)+0.6581*AR(3)+ε。
(四)模型的预测
根据以上建立的模型对GDP作2000~2015年的预测值,并与实际值进行比较,可知预测值和实际值的总体差异较小,说明模型预测的效果较好,此模型可以用于预测。
三、结论
在时间序列中,平稳时间序列主要有三种类型,自回归(AR)模型、移动平均(MA)模型和自回归移动平均(ARMA)模型,这三种模型都是线性模型,他们能用有限的参数刻画时间序列的动态性。尽管线性关系的假定在解决实际问题时是一个比较苛刻的条件,但无疑是理论研究的基础。[2]对于一个时间序列进行模型的识别,然后不断地进行建模的实验,并辅以相关的诊断技术,根据情况再进行适当的调整,继续进行识别、估计、检验等环节,直到模型通过检验,达到最优模型为止。本文中关于GDP的原始数据显然是不平稳的,针对非平稳的序列,通过差分、取对数等方法,可以将非平稳的数据变成平稳的序列,以便能够有效地进行预测。
(作者单位为河北农业大学经济贸易学院)
参考文献
[1] 何新易.基于时间序列模型的中国GDP增长预测分析[J].财经理论与实践(双月刊),2012,33(178):96-99.
[2] 史代敏,谢小燕.应用时间序列分析[M].北京:高等教育出版社,2011:24-25.

