“负数的认识”教学研究报告

株洲市天元区栗雨小学数学教研组 潇湘数学教育工作室



“负数的认识”教学研究报告

株洲市天元区栗雨小学数学教研组 潇湘数学教育工作室

一、问题

1.对教材的分析

“负数的认识”是在学生认识了自然数、分数和小数的基础上学习的，是从算术数到有理数的第一次扩充，这是对数概念的进一步丰富，为初中阶段进一步理解有理数的意义和运算作铺垫。在小学阶段认识正负数的概念，一方面可以丰富学生对数概念的认识，另一方面可以防止学生形成算术思维的定式，有利于学生代数思想的建立和抽象思维水平的提升。

人教版教材从观察气温引入负数，既能让学生体会负数产生的现实意义，又能帮助学生体会到正负数的相对性。具有相反意义的量在现实生活中是大量存在的：存款与取款，收入与支出，上车与下车，电梯楼层标识，等等。因此，教师在教学中为孩子们提供丰富的、现实的负数情境并不困难。这些生活背景大都出于计数的需要，符合学生的认知起点，与负数产生的历史也非常吻合。事实上，负数的产生，既有现实生活的需要，也有数学本身发展的需要。一些教师也会采用算术运算的方法引入负数（一个较小数减去一个较大数，其差便是一个负数）。对于小学生而言，这种引入方法虽然极易被接受，也可以在一些现实的问题情境中找到直观理解，但大多数学生可能会将这种算法理解为一种规定，所以小学教材中用此法引入的不多。

从数概念教学的一般规律而言，新概念的教学并不是孤立的，往往要与旧的概念一起形成新的概念系统。负数的认识自然离不开正数与0。对温度计的观察，可以有效地帮助学生逐步从直观到半直观再过渡到比较抽象地认识正数、负数和0三者之间的关系，温度计“横过来”便可成为数轴的雏形。因此，利用温度计这一直观教具有利于帮助学生丰富数的认识，理解0是正、负数的分界点。教材中没有这种安排，教师利用温度计模型制成教具也不失为一种直观的教学资源。

2.对教学的分析

（1）如何引导学生在已有经验的基础上理解负数的本质意义？负数认识以儿童的经验为起点，但如果处理不当，学生最终还会停留在原来的经验里。那么，小学阶段对负数的初步认识是不是就等同于生活层面上的认识？这种认识还极为肤浅和片面，主要体现在：认为“负”就是“减少”或“少”，“正”就是“增加”或“多”；负数就是负整数、负小数（负分数）；0算作正数还是负数都无关紧要；对正数和负数的理解仅限于形式上，如看到+16和-16，学生主要从符号上将两者区别，对两者之间的相反意义则难以理解；大部分学生会以为-m是负数，这种影响到了中学也需要相当长一段时间才能得以纠正。

（2）如何把0和正数、负数的意义沟通起来？数学史上之所以有不少数学家把负数称之为“荒谬”的数，大都因为对0的局限认识——认为“0表示什么都没有”。可见，对负数概念的理性认识，困难之处不仅在于概念本身的高度抽象性，更在于如何引导学生跨越和扩展已有的认识，也就是把0和负数的意义沟通起来。那么，在认识负数的教学过程中，如何在具体经验的层面上引导学生体会0和正数、负数的关系，体会0还可以表示分界点、标准量？这是教学中的难点，也是把负数纳入到已知数系的关键点。

（3）到底如何定位小学阶段负数的认识这一内容的教学目标？从现有中小学教材来看，负数的认识在小学阶段和初中阶段都有出现，单从概念引入来看，呈现形式大同小异。这一点可以理解为知识系统性的需要，无可厚非。尽管《数学课程标准》中对负数的认识有了较为清晰的表达，但越来越多的老师（主要是名师）尝试从不同的角度定位本课的目标。有的以认识相反意义的量为主，有的侧重于对0的新认识。笔者所在的数学组在进行同课异构时，有一位老师模拟名师的教学设计了一个问题情境：“原来文老师在5楼，他从5楼往上2层楼，记作+2层，那他从5楼下去1层，记作（ ）层，这里把（ ）看作了0层；现在李叔叔在2楼，如果把2楼看作0层，他往上2层，记作（）层。同样是4楼，为什么一会儿被记作-1层，一会儿被记作+2层？”这样设计的目的是希望让学生认清0表示的是标准量，但很多学生被具体楼层和所谓的记法弄得云里雾里，最终也只能靠教师来自圆其说了。

（4）数学史的渗透与概念形成之间的矛盾。在小学上负数的认识一课时，几乎所有的老师都不会忘记渗透数学史，其中大部分老师会采用课件或画外音的方式对负数的产生进行介绍，目的是让学生知晓负数的产生经历了非常曲折的发展过程，从而感受到人类祖先在发明创造数中的伟大智慧。事实上，这种渗透往往如隔靴搔痒，很难给学生留下深刻的印象。我们也见过一些名师在教学中突出体现了具有相反意义的量甚至是标准量（0）等这些发展中的关键之处，但这些过程的经历不但不能帮助学生还原负数的生成过程，反而会让学生心生困惑：这么简单的问题，为何老师要大费周章？古人为何那么愚笨？

3.对学情的分析

学生在生活中接触过一些表示相反意义的量，如：班上转入多少学生、转出多少学生，气温零上多少度、零下多少度，加分、扣分，存款与取款，等等。学生对+、-这两个运算符号已经不陌生，凡是坐过电梯的学生（哪怕是幼儿）对用“-”（负号）表示地下的楼层也不陌生；部分学生早就知道诸如3-5=-2之类的较小数减去较大数的运算。但学生不容易理解负数、正数与0的关系。对负数的形式，有“-”（负号）比较容易识别，对负数的现实意义比较容易理解，但多数学生更容易理解带“-”（负号）的数叫负数，因此，提供大量运用负数的机会，渗透和建立代数的意识，为有理数运算打好基础是本节课的提升点。

4.解决的策略

基于以上分析，我们确定本节课的教学目标和策略如下：首先，从生活情境出发，引发认知冲突（怎样用合适的数表示零下的温度），调动生活经验，主动接纳负数概念；然后借助海拔高度、存取款、进出货等现实问题进一步体验相反意义的量及负数的意义；接着通过比较、反思、归纳等辨析活动帮助学生沟通新旧知识之间的内在联系，促进学生对负数概念内涵与外延的完整认识；最后通过适当的生活应用练习，丰富学生对负数概念的理解和建构。如此，通过有层次的探究活动，引领学生主动建构，发展学生的数学思维能力。

二、实践

1.基于在学生已有经验基础上理解负数的现实意义的教学尝试

片段目标：结合现实情境帮助学生认识和理解负（正）数的现实意义。

师：下面有几组信息，请同学们用自己的方式记录在活动单中，关键是让别人一眼就能看明白。（课件呈现）

●株洲昨日最高气温是31℃，内蒙古去年最低气温是零下31℃。

●妈妈今年4月初存入5000元，4月底又取出5000元。

●水果店上午进了120个西瓜，卖出58个。

●珠穆朗玛峰高于海平面8844.3米，吐鲁番盆地低于海平面155米。

活动单：

（1）用合适的方式将数据信息记录在表格中。

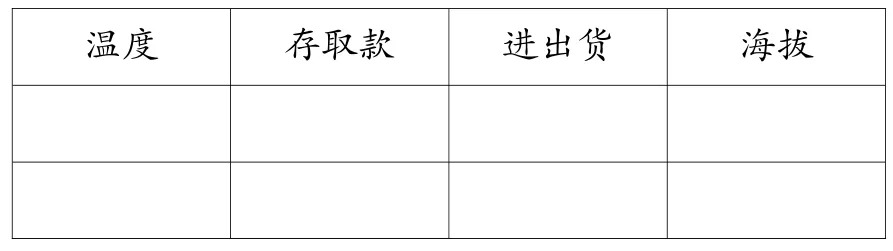
温度 存取款 进出货 海拔

（2）小组交流，想想哪种记录方法更好。

学生先独立思考，然后在小组内交流并汇报。

组1：我们组有几种不同的记录方法，但都是在数据前加了文字或符号。经过商量，我们统一在数据前加了一组反义词，这样别人一眼就能看明白。

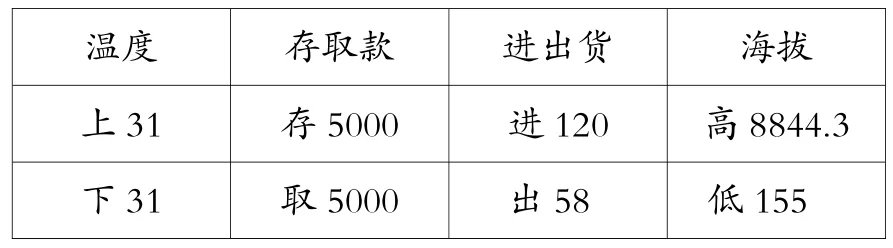
温度 存取款 进出货 海拔上31 存5000 进120 高8844.3 下31 取5000 出58 低155

师：老师特别喜欢你们加的这一组反义词，简单又明了！

组2：我们组原来也有同学用了组1的方法，但我们觉得这种记录方法还是麻烦，于是用符号表示，让人一目了然。

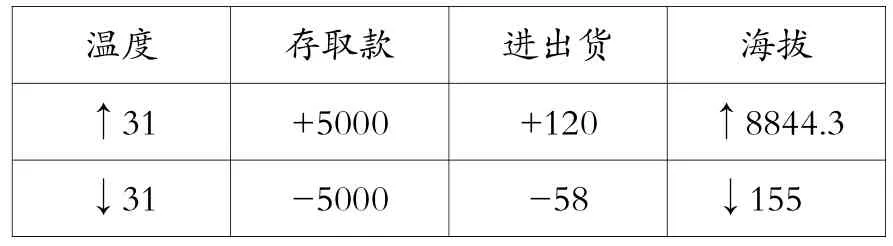
温度 存取款 进出货 海拔↑31 +5000 +120 ↑8844.3 ↓31 -5000 -58 ↓155

师：高的用向上的箭头，低的用向下的箭头，增加了用+，减少了用-，确实更简洁。

组3：……

师：数学语言既要简洁，又要大家都能够看明白。这些记录方法都有道理。如何让大家都明白呢？

生1：我们可以统一用+和-表示。如，存入用+，取出用-。

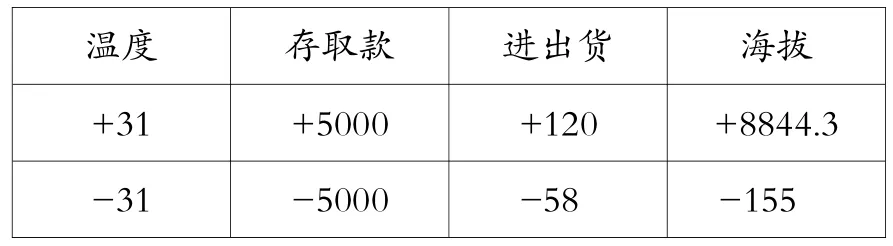
温度 存取款 进出货 海拔+31 +5000 +120 +8844.3 -31 -5000 -58 -155

师：你的想法和数学家的不谋而合！（课件呈现完善后的记录表）这样，上面这一排数都可以在数的前面添+表示，我们把这些数叫作正数，下面这一排数都可以在数的前面添-表示，叫作什么？

生2：负数。

师：这里的加号和减号与过去的意义不完全相同，+叫作正号，-叫作负号。观察表中上下两个数所表示的量，你们有什么发现？

生3：它们表示的意思相反。

师：虽然我们把文字换成了符号，但这两个符号仍然能像反义词一样表示相反的意思。其实，我们还可以更简洁，上面这排数不加符号，下面这排数加“-”。（课件呈现修改后的记录表）为了表示两种相反意义的量，出现了一种新的数：负数（圈出第二排的数）。而以前所学过的31、5000、120、8844.3这样的数叫做正数。正数前面的+可以省去。

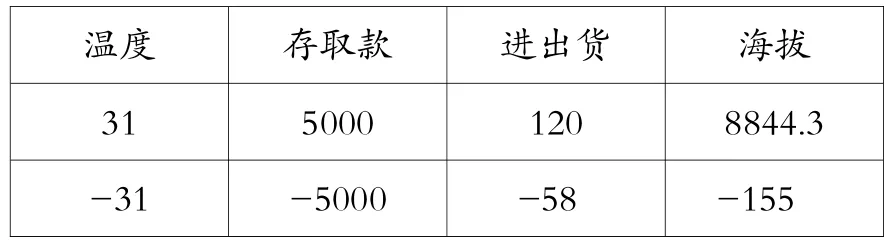
温度 存取款 进出货 海拔31 5000 120 8844.3 -31 -5000 -58 -155

设计意图：负数的出现，是表示生活中两种相反意义的量的需要。本环节通过生活中学生感兴趣的素材，唤起他们已有的生活经验，激发学习兴趣，让他们在具体情境中感受负数出现的必要性，并通过两种相反意义的量的对比，初步体会负数的现实意义，建立负数的概念。

2.基于沟通0与正、负数的关系的教学尝试

片段目标：借助温度计帮助学生理解0与正、负数的关系，感知数轴模型。

师：0是正数还是负数？

生1：0既可以算正数，也可以算负数。

生2：0既不是正数，也不是负数。

师：（出示温度计模型）请同学们找找，在温度计上，0℃在哪里？比0℃高的温度，都是什么数？

生3：比0℃高的温度，都是正数。

师：那比0℃低的温度，都是什么数？

生4：比0℃低的温度，都是负数。

师：如果0℃算是一个正数的话，那么-0℃在温度计上的哪里呢？

生5：还在原来的位置。

师：既然这两种表示方法没有相反的意义，我们就规定，0既不是正数也不是负数，它只是正负数的分界点。+3和-3有什么不同？

生6：在老师批阅试卷时，+3表示加3分，-3表示扣3分。

生7：在温度计上，+3表示零上3℃，-3表示零下3℃。

师：（再次指着温度计）+10℃在哪里？-6℃在哪里？（随着学生的汇报，师将学生汇报的数写在黑板上，追问）说说还在什么地方见过负数？你能不能试写几个负数？

生8：-1、-2、-3、-4……

师：还有不一样的吗？

生9：-1.2、-2.5、-3.5、-4.5……

生10：-1.1、-1.2、-1.3、-1.4……

生11：-

……

师：写得完吗？

生（齐）：写不完，负数也有无数个。（师随着学生的汇报，把所写的正数和负数分别圈起来，加上“……”）

师：如果把负数、0、正数按照从小到大的顺序排列，该怎样排呢？为什么？

生12：负数＜0＜正数。大家看，从温度计上可以看出，正数都在0的上面，比较大，负数都在0的下面，比较小。

师把温度计横过来，形成如下图的板书——

设计意图：这一环节重在引导学生弄清楚0和正数、负数之间的关系，初步渗透集合思想。教师在引导时，再次利用温度计这一工具初步帮助学生建立数轴模型。

3.兼顾巩固应用和拓展延伸的练习片段教学

片段目标：在更多的生活实例中帮助学生巩固对正、负数的认识，加深对概念的理解。

师：负数在生活中有着广泛的应用，大家独立完成下面的练习。

作业单：

（1）叔叔上5楼开会，按5键，阿姨到地下2楼的车库取车，应按（）键。

（2）知识竞赛中，五（1）班得了20分，记作+20，五（2）班的得分是-20，表示（）。

（3）王阿姨经营了两个商店，5月份，A商店赚了3000元，B商店亏了500元，可以分别用（ ）和（ ）表示。

（4）小华从0点向东行5米表示为+5，那么从0点向西行3米表示为（）米。

（5）吐鲁番盆地比海平面低155米，记作-155，莲花峰比海平面高1864米，记作（）。

（6）产品说明书上的负数：食品包装袋上有这样的标记500±2g，质检人员拿出5袋称重后和标准重量比较，记录为：+0.1g、-1g、0g、+0.5g、-1.5g。+0.1g、-1g、0g、+0.5g、-1.5g是什么意思？500±2g是什么意思？

学生独立完成，师点名汇报，根据实际情况点拨。点拨要点如下：

（1）一楼及以上的楼层前省略了正号，其实都是正数。

（2）追问：这两个班的得分相差多少？为什么？

（3）总体来说王阿姨经营两家店是赚了还是亏了？

（4）如果规定向西行为正，那记法还一样吗？

（5）0表示什么？（海平面）

（6）你觉得质检人员会认为这种食品标记合格吗？

设计意图：再次提供多种包含具有相反意义的量的生活情境，丰富学生对正、负数的相对性的认识，并学会正确使用负数表示具有相反意义的量，有利于学生对数概念的结构认识，适时的追问均是对有负数参与的代数运算的启蒙。第（1）题是为了加深对正数实际写法的理解；第（2）题是引导学生从直观的角度感知有理数的运算；第（3）题则把有负数参与的加法运算与之前学过的减法运算联系起来；第（4）题是帮助学生进一步体会正、负数的相对性，渗透正方向；第（5）、（6）题巩固了学生对0是分界点、0是标准量的认识。

4.基于对负数意义的深化理解的教学尝试

片段目标：深化学生对负数的认识。

师：世界各国对负数的认识和接受有一个过程。如1484年，法国数学家曾得到方程的一个负数解，但他不承认它，说负数是“荒谬”的数。1545年，卡尔丹承认方程中可以有负数解，但认为它是“假数”。1831年，还有数学家认为负数是虚构的，他举了一个“特例”说明他的观点：“父亲56岁，他儿子29岁，问什么时候父亲的岁数是儿子的两倍？”通过列方程解得x=-2，他认为这个结果是荒唐的。同学们，你们怎么看待x=-2这个结果呢？

生：-2正是说明2年前父亲的岁数是儿子的两倍。

设计意图：用数学史中的小故事挑起疑问，再揭示负数在数学中的生命力，既利于学生理解负数的意义、激发学习的兴趣与积极性，又利于体现数学思想与方法的价值。

三、讨论

1.对课堂的思考

关于数概念。数既是对生活的抽象表达，又广泛应用于生活之中。数的出现除了生活实际的需要，也有数学本身发展的需要。在帮助学生建立数概念的过程中，如何两者兼顾，值得好好研究。

关于数概念教学。小学阶段，数学老师们对已知数系的结构定然是了如指掌，但现实的情况是，这些概念分布于不同的阶段，如果不注意沟通概念之间的关系，便很容易出现割裂化的状态，也就是学了新的忘了旧的，数概念越多，关系越模糊。因此，如何使学生形成结构化的认知，克服仅仅从表面的符号去认识数的行为，是课堂中首先要解决的问题。本课虽然有了对正、负数及0之间关系的沟通，但仍未能避免学生产生“带负号的数就是负数”的片面认识。

2.提出新问题

（1）据资料显示，有关负数的教学安排最早出现在1978年的《小学数学教学大纲（试行草案）》中。该大纲对五年级提出了“初步理解正、负数的意义，能够正确地进行简单的正、负数四则运算”的要求。但1986版的大纲又把这部分内容删了，直到2001年《义务教育数学课程标准（实验稿）》颁布，认识负数的教学内容重新回归小学数学课堂，但不同版本的教材把这个内容放到了不同的年级，北师大版放在四年级，人教版则放在六年级，其教学目标也不尽相同。2011版课标保留了这个内容，其教学目标仅限于“在熟悉的生活情境中，了解负数的意义，会用负数表示日常生活中的一些量”。显然这个目标强调了联系生活实际，但与1978年的教学大纲相比，则降低了要求。在小学认识负数，最大的价值在于有理数系统的完善，而要更全面、系统地理解负数，中学开始即可。负数的难度也不在于认识负数本身，而在于有理数运算中有关负数的运算，这是学生最容易弄错的。那么，到底把“负数的认识”放在哪个年级段合适？估计目标制定者、教材编者们也尚无定论。

（2）数概念的高度抽象性使得它的本质意义很难被普通人所理解，自然数、分数、负数、有理数、无理数、实数、虚数、复数……这些简单的名称背后都有丰富的生活背景和数学背景。只有将其与具体的背景结合起来演绎，学生的认知才会变得丰富和生动。然而，这种人为的经历难免陷入活动化的假象中，有时甚至会一发不可收拾。如何在有限的时间内让学生经历探究的过程，始终是摆在老师们面前的一个难题。 （执笔：何亩文）