数学认知思维序与有效教学策略（上）

邓友祥



数学认知思维序与有效教学策略（上）

邓友祥

1　一道测试题引发的问题

当前，初中数学新课程实施已经进入“深水期”，但我国初中数学新课程改革在取得显著成绩的同时，仍存在不少有待解决的问题。比如，初中生数学学习粗心的现象仍较普遍；不少初中学生独立思考的意识不强，缺乏深度的数学思考；部分初中学生感到上课能听懂，但解答稍复杂的数学问题时，往往不知所措。不少数学教师和教育工作者（甚至包括学生和家长）都将此类现象的发生简单地归结为教师的课程理念、教学方式、教学方法或是学生的学习兴趣、学习态度、学习方法等存在问题。这种抽象空泛的原则性认识并不能从根本上找到问题发生的原因和有效的解决办法。笔者认为，上述现象的主要根源还在于初中生的数学思维存在诸多不良习惯。为了获得真实的评判结果，我们曾经对本市S校初一学生进行了如下测试。

苏教版七年级（上）教材中“丰富的图形世界”这部分内容有如下一道习题（如图1）：

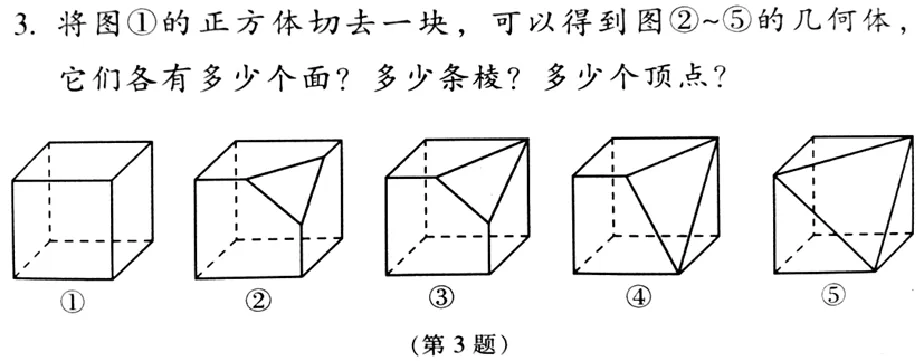
图1

这种静态性的数学问题，直观性强，思维容量较小，几乎所有学生都能给予正确解答。为了测试学生真实的数学思维活动，我们隐去图②～⑤，仅出示图①，将此题改编成具有较大思维容量的动态题（仅供本次思维活动测试用，不作为常规教学用），让本市S校初一学生思考探究：“将图①的正方体切去一个角，得到的几何体各有多少个面？多少条棱？多少个顶点？”结果正确解答该题者只占测试人数的31.3%。不能正确解答该题者，主要原因在于不能正确画出4种类型的截面图，从而发生了漏解（绝大多数学生丢失了情形③或④）。

为了弄清问题产生的根源，笔者进行了跟踪抽样访谈。发现其中正确者，较多地表现出如下解法：有的学生考虑到截面三角形的顶点与正方体的顶点重合的个数，分别有0、1、2、3个，共4种情形，顺利地画出图②～⑤，从而得解；也有的学生考虑到正方体的棱被完全截去的条数，分别有0、1、2、3条，同样可画出图②～⑤，进而得解；还有的学生思维较灵活，先画出常规图形②，然后变“静”为“动”，让截面三角形的顶点C、B、A分别依次沿正方体的棱移动（如图2），从而较易地得出图③、④、⑤，进而获解。

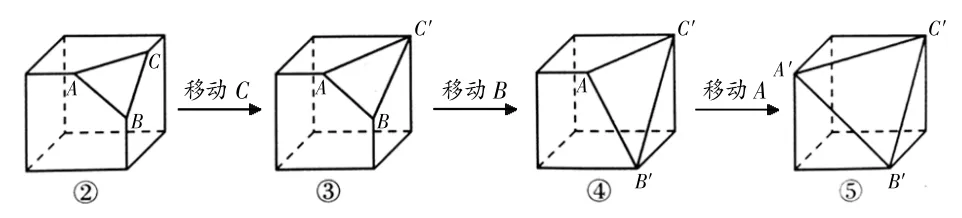
图2

显然，给出正确解答的学生在解答本题时数学活动（思维活动）是有一定心理顺序的，而且这种顺序表现出较强的逻辑性。相反，几乎所有解答不正确者，思维均处于无序或乱序状态，试图凭感觉（直觉）直接画出图②～⑤，说明此类学生认知思维表现为非逻辑或弱逻辑。

上述分析表明，学生出错的原因主要不在知识欠缺，而是在进行数学思维活动时，其认知思维处于无序（或乱序）状态，或处于有序的非逻辑（或弱逻辑）状态，从而影响了解题策略的选择。由此可见，初中生进行数学问题解决等认知学习时，思维处于有序的强逻辑状态时，确实有助于问题的顺利解决；否则，思维处于无序（或乱序）状态，或处于有序的非逻辑（或弱逻辑）状态时，将严重影响数学问题的解决。初中生进行数学思维活动时，所表现出的这种不同程度的心理顺序就是数学认知思维序。数学认知思维序的差异程度，是初中生数学学习容易发生两极分化的一个重要原因。因此，有必要就数学认知思维序相关问题作出研究。

2　数学认知思维序的内涵与特点

2.1数学认知思维序的内涵

数学认知思维序，是人的感官在对客观世界及自身存在之感知、分析和判断的数学思维活动过程中，反映其数学学习活动的心理顺序。［1］

2.2数学认知思维序的特点

上述提及的心理顺序，主要是指学生心理发展和学习过程的心理顺序。分析数学认知思维序的特点，有助于把握数学活动规律和学生的数学思维活动，采取针对性的有效教学策略，提高数学课堂教学的有效性和学生的数学学习效率。这里所说的特点是指数学认知思维序所特有的性质，通常主要表现为以下几种。

2.2.1主观性

既然数学认知思维序离不开人的感官对客观世界及自身存在之感知、分析和判断，那么其必然带有较强的主观性。这种因人而异的主观性与初中生的数学思维活动水平密切相关，这是数学认知思维序的一个固有特点。

这一特点要求数学教学要充分尊重和发挥学生的主观性，创设有效的情境，加强学生之间的合作交流，充分暴露学生的数学思维，以便采取针对性的有效教学策略，帮助学生建立良好的数学学习活动的心理顺序。

2.2.2思维性

众所周知，学生从事任何数学学习活动均离不开数学思维，思维性理应是数学认知思维序的一个基本特点。鉴于数学认知思维序带有较强的主观性，反映的是数学学习活动的心理顺序，因此，学生的数学思维有时是逻辑的，有时是非逻辑的（顿悟、灵感等）。另一方面，数学学习最终都应落实到使学生消除不理解的学习内容上去，初中生（尤其是初二学生）的逻辑思维发展处在一个十分关键的时期，任何忽视逻辑的数学教学都是不成功的，因为没有使学生的逻辑思维得到本质上的发展。

因此，这一特点要求数学教学要向学生提供具有探索性和思考性的数学学习任务，在充分利用并发挥学生的顿悟、灵感等直觉的非逻辑思维得出相关结论后，引发学生进行深度的数学思考，并促使学生依据概念、规则（法则、公式、性质、定律、定理等）进行数学思维，通过逻辑推理得出科学结论，逐步发展学生的逻辑思维。

2.2.3差异性

由于数学认知思维序反映的是学生数学学习活动的心理顺序，也就是学生心理发展和学习过程的心理顺序，而且个体心理发展在发展进程、内容、水平等方面具有千差万别的特殊性，因此，数学认知思维序具有差异性这一显著特点。

这一特点要求数学教学要充分尊重个体心理发展的特殊性，数学教学活动设计要有一定的层次性，教师向学生提供有效认知数学任务的同时，应针对不同认知水平层次的学生，提供合理的数学学习支架。

2.2.4拟容性

数学学习活动具有较强的内隐性，这是由于表面上看数学学习活动较多的是外在的活动（解题等操作活动），事实上数学学习活动更多的应是其内在的活动（数学思维活动），离开内在活动的任何外在数学学习活动是没有意义的。内在的数学思维与外在的数学操作如何才能实现有机融合呢？是数学认知思维序发挥了“拟容”作用。思维在认知过程中具有的“拟它化”和“相加”的特性，就是认知思维序的拟容性。所谓“拟它化”，就是思维在认知过程中把那些统统不属于、不相干拟化成被认知事物，从而经过大脑的思维加工，将之与已有认知结构进行“相加”（有机融合）重组，形成新的有序的认知结构。［2］这是认知思维序的内在特点，也是核心特征。

这一特点要求数学教学应该引导学生正确表征数学问题，加强对学生抽象概括和数学反思能力的培养，促使学生积极参加解题等外在操作活动，从而揭示自身内在的数学思维活动，使外在操作与内在思维实现有机统一。 （待续）