砂土中吸力式桶形基础竖向承载性状研究

李大勇，吴宇旗，张雨坤

(1.山东科技大学 山东省土木工程防灾减灾重点试验室，山东 青岛 266590；2.山东科技大学 土木工程与建筑学院，山东 青岛 266590；3.河海大学 土木与交通学院，江苏 南京 210098)

砂土中吸力式桶形基础竖向承载性状研究

李大勇1，吴宇旗2，张雨坤3

(1.山东科技大学 山东省土木工程防灾减灾重点试验室，山东 青岛 266590；2.山东科技大学 土木工程与建筑学院，山东 青岛 266590；3.河海大学 土木与交通学院，江苏 南京 210098)

摘要：吸力式桶形基础的竖向承载力是工程设计中的重要问题，其承载力主要由桶壁摩阻力、桶尖端承载力及桶内部土体的支撑力三部分组成。在同种砂土地基中桶基础的直径、桶高以及在地基中的埋深直接影响着上述三部分力的大小。分析了桶壁摩阻力和桶尖端承载力随埋深的变化关系式，提出了计算地基承载力的解析表达式。并通过试验数据验证解析式的准确度，结果两者误差均在15%以内,所提出的解析表达式适用于地基承载力的计算。

关键词：砂土地基；吸力桶基础；竖向承载力；滑移线理论

吸力式桶形基础是一种上端封闭，底端开口的钢制海洋工程基础结构，因其施工简单、施工速度快、造价低及可回收利用等优点而被用于系泊海洋浮动式结构及海洋平台基础[1-2]，近年来也逐渐被应用于海上风电塔架的基础[3]。国内风力发电平台快速增长[4]，对桶基础极限承载力的研究越加迫切，桶形基础往往承受着来至上部风力发电机及塔架的巨大载荷，承载能力与其直径、高度密切相关。国内外许多学者通过模型试验、离心机试验、数值软件分析及理论推导等方法对竖向承载力做了大量研究。Bransby[5]、Sharma[6]和Gourvenec等[7]通过有限元方法研究了吸力基础在水平和竖向荷载以及弯矩复合荷载作用下的承载力，得出吸力基础的承载力极限包络图以及吸力基础桶裙长度对包络图的影响。Hung等[8]借助有限元法讨论了不同的不排水抗剪强度下吸力基础的承载力随长径比的变化，并分析了桶基础在竖直和水平荷载作用下运动形式和基础周围土体的破坏机理。武科等[9]在饱和软粘土中对桶基础的分析，得到竖向荷载作用下的极限承载力，提出软粘土的不排水抗剪强度、土体各向异性以及吸力基础的长径比都是影响吸力基础竖向承载力的主要因素。刘振文等[10]通过有限元计算,研究了单桶基础的竖向破坏模式,基础埋深范围内土体强度以及基础形状对地基竖向承载力的影响。刘梅梅等[11]通过有限元计算，得到竖向加载作用下不同长径比的桶型基础承载特性及桶型基础的失效形式，提出计算极限承载力时可将桶内土与桶作为一个整体简化分析。张宇等[12]对桶形基础的不同部位在承担竖向荷载中的比例变化进行分析，得到桶顶板土反力、侧壁摩阻的分布形式和桶尖端部阻力的特点。同时，进行了竖向下压载荷作用下桶形基础的模型试验及非线性数值分析，计算结果与模型试验结果吻合比较好。张金来等[13]研究不同高径比的情况下，桶基础的竖向承载力和竖向位移的关系曲线，得出模拟计算结果和试验结果相近。武科等[14]基于上限法理论建立了一种竖向荷载作用下极限分析模型，利用有限元计算验证了建立的极限分析模型的可靠性，得出土体各向异性、桶基础的长径比及软粘土的不排水抗剪强度是影响吸力基础竖向承载力的主要因素。矫滨田等[15]对吸力式桶形基础在竖向动载荷作用下进行离心机试验模拟得到：当在竖向动载荷作用下载荷幅值超过一定限值时，桶基周围砂土将会发生软化甚至液化,桶基则会发生明显的沉降。桶基周围土体的沉降量随着载荷幅值的增加而增大。很多学者基于有限元软件开展了桶基竖向承载力的特性研究，并与模型试验结果进行比较，结果较为理想。

基于极限滑移线理论，假定滑移区的土体为无体力的理想刚-塑性材料，依据土体进入塑性阶段时的应力平衡状态，通过滑移线理论推导出了极限承载力与沉陷深度关系的解析式。并结合了室内试验数据进行验证，得出的解析表达式具有一定的准确度，并且对预测承载力的变化走势以及对桶基础承载力的确定有一定参考。

1吸力桶基础竖向承载力解析解

图1　吸力桶受力分析

在吸力桶承载过程中，桶受到土体对桶的内、外壁摩擦阻力、端部阻力和内部土体对桶盖的支撑反力。内壁摩擦力与桶内部土体和桶盖之间的应力水平相关，由于作用在桶顶板上的大部分载荷通过内部土柱继续向下传递，且桶内部土柱与桶体一起运动，故可以把桶和桶内土体作为一个整体进行分析，类似实心桶承载模型。此时，桶壁的内摩擦力和顶板处与土体的相互作用力视为内部力，在计算过程中不用考虑、简化了计算。桶和内部土体作为一整体,当产生沉陷量S时，其受力如图1所示。图中,ho为桶裙的高度；F为极限承载力；G′为吸力桶和桶内砂柱整体的浮重；Fout为桶外壁摩擦力；Fend为桶端部阻力；σi为整体受到的底部的均匀应力；Ri为桶内半径；Ro为桶外半径；Rm为桶平均半径；hw为水深。

1.1吸力桶外侧摩擦力

在任意深度z处，桶外侧竖向有效应力为σ′=γ′z，γ′为土的浮重度。沿桶壁竖向土侧压力σ=K0σ′=K0γ′z。则在桶外表面上的任一微平面dA=Ro·dθ·dz上桶外侧的摩擦力大小为：dFout=K0γ′ztanψ·dA=K0γ′ztanψ·R0dθdz。则在整个桶外壁上的摩擦力为

(1)

其中：K0为侧压力系数；Ro为吸力桶外半径；ψ为砂土和桶基础的摩擦角；γ′为砂土的浮重度；h0为吸力桶高度；S为吸力桶贯入地基的深度。

1.2吸力端部阻力

在吸力桶沉贯过程中桶壁底部厚度范围内的土体对桶底部产生阻力，阻力的大小可由Terzaghi地基承载力公式计算。对砂土材料，其内粘聚力为零。则端部阻力为

Fend=2πRmt(σ′Nq+γ′Nγt)。

(2)

其中:t为吸力桶壁的厚度；Rm为吸力桶平均半径；σ′为吸力桶端部的有效应力；Nq和Nγ分别为Terzaghi地基承载力系数。

1.3桶端部地基土体发生剪切破坏时的极限应力的滑移线解(Hill)解

吸力桶基础承受着巨大的上部风电结构的重力，承受较大的竖向载荷。这部分载荷直接传递给桶底部地基土体，当载荷达到或超过地基土体屈服条件时，土体进入塑性状态。桶的沉陷深度已知，所以作用在桶尖端外侧土体AB上的正应力σo大小已知，可求得ABC区域的平均应力大小，根据建立的塑性区沿滑移线平均应力的变化关系求解OAD主动区内的平均应力大小，求得作用在OA上σi大小，最终根据图1中整体的受力分析可求得桶的极限承载力。

图2　吸力桶尖端内外滑移线场图

假设塑性滑移区域(图2中OABCD区域)土体为理想刚-塑性材料；不计此部分土体体力和滑移面上的摩擦力；土体屈服时满足摩尔库伦屈服条件；在荷载作用下，土体中的塑性区域在某些方向可以自由流动；由于发生塑性流动土体塑性变形较大，弹性变形可以忽略。把作用在桶底部外侧AB上的应力简化为均布的等效超载计为σo；作用在桶内侧OA上的应力简化为等效超载σi，如图2所示。图中,F为桶基础的极限承载力；hw为水深；S为沉陷深度；h0为桶基础的高度。

1)主动区OAD平均应力求解

在桶处于沉陷深度S处，土体进入塑性阶段。此时由于作用在OA和AB上的应力简化为等效的恒定超载。取OA上任一微元体分析，则作用于直的边界OA上的正应力为：σn=σi=const，剪应力τn=0，为定值边界条件构造匀应力场。考虑桶内土体主动下滑为主动朗肯区，σn=σi>σt，可判定σt为小主应力，σn为大主力。此区域平均应力通过图3中的几何关系求解。

图3　OAD区域极限应力状态

根据图3所示的极限应力关系，可求得OAD区域土体的平均应力

可得在D点处的平均应力

(3)

2)被动区ABC平均应力求解

分析桶外侧的土体，作用在直的边界AB微单元上正应力为σn=σo=γ′(h+h0)=const，τn=0。同样构造均匀应力场，考虑此部分土体被动上移，为被动朗肯区σn=σo<σt，σn小主应力，σt为大主应力。

图4　ABC区域极限应力状态

根据图4所示的应力状态，可求得被动区ABC区域土体的平均应力大小为

可得C点处的平均应力

(4)

3)过度场ACD平均应力求解

对饱和细砂等摩尔库伦材料，内粘聚力c=0。满足非正交流动法则，滑移线与大主应力作用面的夹角为：45°+φ/2，在过渡区ABC范围内，过渡区两侧与均匀应力场相接，故α族滑移线为直线；又因为两族滑移线夹角为90°±φ，可得β族滑移线为对数螺旋线。土体的摩尔库伦屈服面和极限应力圆的关系如图5所示。

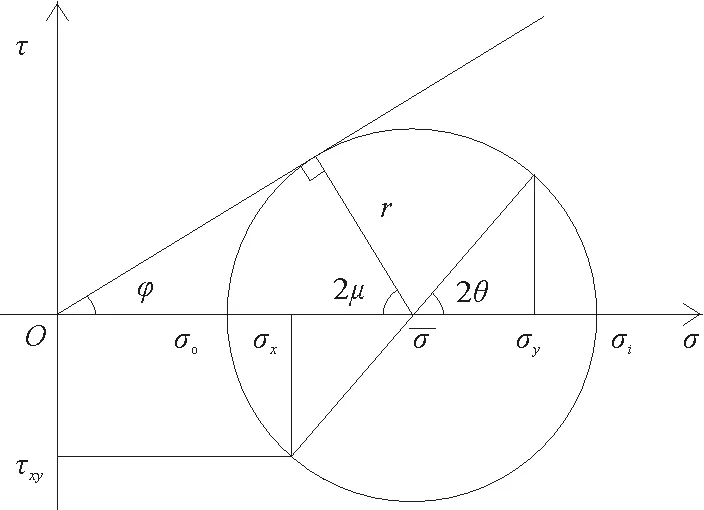
图5　砂土摩尔库伦屈服面和极限应力圆的关系

根据应力平衡方程:

(5)

并由图5可得：

(6)

将式(6)代入式(5)可得:

(7)

(8)

求解上述方程可得α、β线方程为

(9)

式中的C为常数，可由初值条件确定。

由于大主应力作用线穿过由α、β线构成的右手直角坐标系的一、三象限。最终构造的整体滑移场及α、β线方向如图2所示。其中OAD区域主被动滑移区，ABC区域为被动滑移区，ACD区域为中间过渡区。根据滑移线性质，在β滑移线上：

(10)

将式(3)、(4)代入式(10)得

(11)

整理式(11)得

(12)

1.4竖向力的平衡求解承载力

桶基础受力分析如图1所示，由竖向力的平衡可得：

(13)

其中，G′为桶基和桶内部砂柱浮重。

将式(1)、(2)、(12)代入式(13)，可得桶竖向承载力

(14)

2解析解的验证

通过室内模型试验得到的数据对解析式进行验证。砂土物理参数由室内试验测得。试验器材包括模型桶、模型箱、加载设备、数据采集仪等。试验在相同的条件下重复多组，取相对稳定的数据对解析解验证。

表1　砂土的计算参数

2.1试验用砂

采用同一批试验用砂[16]。基础模型为钢制桶，尺寸为直径×高度=0.12 m×0.24 m。模型箱材料为镀锌钢板，尺寸为：长×宽×高=1.0 m×1.0 m×0.8 m，其尺寸能够消除边界条件对试验过程的影响。模型箱底部设有排水阀门，用来控制模型箱内砂土排水固结，使之达到很高的相对密实度。利用文献[16]中的砂土计算参数可求砂土浮重为10.5 kN/m3，砂土物理力学参数如表1所示。

2.2试验过程

试验开始前将砂土排水固结，固结完成后采用压贯方式将打开排水孔的桶基础压入地基中至顶板与地基表面接触为止，静置24小时，之后以很小的贯入速度继续压贯，直至压入一倍桶高深度结束。

2.3试验数据分析

提取试验数据，竖向承载力和竖向沉陷位移之间的关系如图6所示。

图6　竖向承载力和竖向位移的关系

分析试验数据可知，起初阶段OA，地基土体接近弹性阶段，其应力-应变曲线近似一直线。随着力的增加(AB段)，土体颗粒原有的排布形式已经达不到抗剪强度，土颗粒之间开始相互错动并重新排列，土体更加密实、内摩擦角增大，抗剪强度增大。随着载荷的增加，曲线到达图中B点，内摩擦角达到峰值内摩擦角，抗剪强度达到峰值，此点即达到了地基的极限承载能力。重新排布后的砂土颗粒之间的剪应力达到其极限抗剪强度时，紧紧咬合在一起的土颗粒开始被剪裂或者剪碎，内摩擦角小于峰值内摩擦角，抗剪强度降低。砂土体出现软化并产生较大的变形，表现在图6中BC阶段，承载力有减小的趋势而竖向位移增加较快。最后，随着沉陷深度的继续增加，原有的塑性区开始向下发展，新的滑移线场不断的在下部土体产生，土体进入CD塑性流动变形阶段。

2.4试验结果与解析解结果对比

分别取不同深度处承载力的实验数据与式(14)理论计算结果进行对比，结果绘制于表2中。可见，两者误差多在10%以内，最大不超过15%，说明式(14)解析解是可靠的。

表2　试验和理论结果对比

3结论

1)理论公式表明，桶基础内部土体提供了较大部分的承载力，而外壁摩擦力及尖端承载力贡献较小。还可看出，地基承载力大小与tanφ成指数增长，内摩擦角的大小对地基承载力大小影响很大。

2)理论解结果和试验数据结果之间的误差在±15%以内，所提出的解析解可用于吸力式桶形基础的承载力计算。

参考文献：

[1]鲁晓兵,郑哲敏,张金来.海洋平台吸力式基础的研究与进展[J].力学进展,2003,33(1):27-40.

LU Xiaobin,ZHENG Zhemin,ZHANG Jinlai.Progress in the study on the caisson foundation of offshore platform[J].Mechanics Advances,2003,33(1):27-40.

[2]施晓春,徐日庆,龚晓南,等.桶形基础发展概况[J].土木工程学报,2000,33(4):68-73.

SHI Xiaochun,XU Riqing,GONG Xiaonan,et al.General conditions of suction caisson foundation[J].China Civil Engineering Journal,2000,33(4):68-73.

[3]BYRNE B W,HOULSBY G T,MARTIN C.Suction caisson foundations for offshore wind turbines[J].Wind Engineering,2002,26(2):145-155.

[4]FENG Y,LIN HE Y,et al.Overview of wind power generation in China:Status and development[J].Renewable and Sustainable Energy Reviews,2015,50:847-858.

[5]BRANSBYM F,RANDOLPH M F.Combined loading of skirted foundations[J].Geotechnique,1998,48(5):637-655.

[6]SHARMA P.Ultimate capacity of suction caisson in normally and lightly over consolidated clays[D].Texas: Texas A&M University,2004.

[7]GOURVENC S,BARNET S.Undrained failure envelope for skirted foundations under general loading[J].Geotechnique,2011,61(3):263-270.

[8]HUNG L C,KIM S R.Evaluation of vertical and horizontal bearing capacities of caisson foundations in clay[J].Ocean Engineering,2012,52:75-82.

[9]武科,栾茂田,范庆来,等.倾斜荷载作用下桶形基础承载力特性研究[J].岩土力学,2009,30(4):1095-1101.

WU Ke,LUAN Maotian,FAN Qinglai,et al.Study on bearing capacity of caisson foundation under inclined loading[J].Rock and Soil Mechanics,2009,30(4):1095-1101.

[10]刘振纹,王建华,袁中立,等.负压桶形基础地基竖向承载力研究[J].中国海洋平台,2001，16(2):1-6.

LIU Zhenwen,WANG Jianhua,YUAN Zhongli,et al.A study on the vertical bearing capacity of caisson foundation[J].China Offshore Platform,2001,16(2):1-6.

[11]刘梅梅,练继建,杨敏,等.宽浅式桶形基础竖向承载力研究[J].岩土工程学报,2015,37(2):379-384.

LIU Meimei,LIAN Jijian,YANG Min,et al.Vertical bearing capacity of wide-shallow caisson foundation[J]. Chinese Journal of Geotechnical,2015,37(2):379-384.

[12]张宇,王梅,楼志刚.竖向载荷作用下桶形基础与土相互作用机理研究[J].土木工程学报,2005,38(2):97-101.

ZHANG Yu,Wang Mei,LOU Zhigang.Study on the mechanism of interaction between caisson foundation and soil under vertical loading[J].China Civil Engineering Journal,2005,38(2):97-101.

[13]张金来,鲁晓兵,王淑云,等.桶形基础极限承载力特性研究[J].岩土力学与工程学报，2005,24(7):1169-1172.

ZHANG Jinlai,LU Xiaobing,WANG Shuyun,et al.The characteristic of the bearing capacity of caisson foundation[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(7):1169-1172.

[14]武科,栾茂田,范庆来,等.滩海桶形基础破坏机制及极限承载力分析研究[J].岩土工程学报,2008,30(3):394-398.

WU Ke,LUAN Maotian,FAN Qinglai,et al.Failure mechanism and ultimate bearing capacity of caisson foundation in shallow water[J].Chinese Journal of Geotechnical,2008,30(3):394-398.

[15]矫滨田,鲁晓兵,张建红.垂向动载荷下桶形基础响应试验研究[J].海洋工程,2009,27(3):45-53.

JIAO Bintian,LU Xiaobing,ZHANG Jianhong, et al.Experimental study on the caisson foundation responses under vertical vibration load[J].The Ocean Engineering,2009,27(3):45-53.

[16]李大勇,冯凌云,张雨坤,等.饱和细砂中裙式吸力基础水平单调加载模型试验—承载力及变形分析[J].岩土工程学报,2013,35(11):2030-2037.

LI Dayong,FENG Lingyun,ZHANG Yukun,et al.Modeltests on lateral bearing capacity and deformation of skirted suction caissons in saturated fine sand under horizontal monotonic loading[J].Chinese Journal of Geotechnical,2013,35(11):2030-2037.

(责任编辑：吕海亮)

Vertical Bearing Capacity of Suction Caisson Foundation in Sand

LI Dayong1, WU Yuqi2, ZHANG Yukun3

(1. Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 2. College of Civil Engineering and Architecture, Shandong University of Science and Technology, Qingdao, Shandong 266590, China; 3. College of Civil and Transportation Engineering, Hohai University, Nanjing, Jiangsu 210098, China.)

Abstract:Vertical bearing capacity of suction caisson foundation is an important engineering problem, which is mainly composed of shaft friction resistance, bearing capacities from caisson tip and supporting force of soil within the caisson. The vertical capacity of foundation is directly affected by the diameter, height and embedded depth of the caisson in the sand. This paper studied the changes of shaft friction resistance and tip bearing capacity when the embedded depth changed and proposed the analytical formulae to calculate foundation bearing capacity. The accuracy of the analytical formulae was testified by experimental data. The results show that the error between them is less than 15% and that the proposed analytical formulae are applicable to the calculation of foundation bearing capacity.

Key words:sand foundation; suction caisson; vertical ultimate bearing capacity; slip line theory

收稿日期：2015-10-16

基金项目：国家自然科学基金项目(51379118)；山东科技大学科研创新团队资助项目(2015KYTD104)

作者简介：李大勇(1971—)，男，山东泰安人，教授，博士生导师，主要从事海洋土力学研究.E-mail：ldy@sdust.edu.cn 吴宇旗(1989—)，男，山东济宁人，硕士研究生，主要从事海洋土力学研究，本文通信作者. E-mail：874993277@qq.com

中图分类号：TU447

文献标志码：A

文章编号：1672-3767(2016)03-0033-07