基于二项分布的快速盲频谱感知算法

苏　杭，叶迎晖，卢光跃

(西安邮电大学 无线网络安全技术国家工程实验室，陕西 西安 710121)

基于二项分布的快速盲频谱感知算法

苏杭，叶迎晖，卢光跃

(西安邮电大学 无线网络安全技术国家工程实验室，陕西 西安 710121)

摘要:基于特征函数的盲频谱感知算法(CAD)检测性能较好但运算量大。利用样本特征构造了新的检验统计量，推导了频谱空闲时检验统计量的概率密度函数和判决门限，分析了所提算法的检测性能和计算量，从而提出认知无线电中基于二项分布的快速盲频谱感知算法。理论分析和仿真表明，所提算法与CAD算法检测性能相当，同时运算量明显低于CAD算法。

关键词:运算量；快速盲频谱感知；二项分布；样本特征

认知无线电(CR)技术是一种动态频谱管理技术，旨在解决当前日益严重的频谱资源匮乏、频谱利用率不高的问题[1-2]，其核心思想是允许次用户(SU)在主用户(PU)不使用授权频段时动态接入该频段，而当PU重新使用授权频段时能够及时撤出，以免干扰PU通信。可见，CR的前提条件和首要任务是频谱感知，即SU可以快速并准确感知频段内是否存在PU信号以实现频谱动态接入和撤出。

经典的频谱感知算法主要有循环平稳特征检测算法、匹配滤波检测算法、能量检测算法(EnergyDetection，ED)、基于协方差矩阵特征结构的感知算法、基于拟合度检测 (GoodnessofFit，GOF) 的感知算法等[2-3]。循环平稳特征检测算法复杂度高，而匹配滤波检测算法必须预知主用户的先验知识(如信号波形、调制方式等)且对于同步的要求也比较高，实际应用有较大限制[4]。能量检测算法不需要得知主用户的任何先验信息，且硬件实现简单，只需要少量采样点便可获得较佳的感知性能，但它需要预知噪声方差，且受噪声不确定度影响[5-6]。基于协方差矩阵特征结构的感知算法[5]克服了这一问题，该类算法利用信号之间的相关性进行检测，主要有基于最大最小特征值之差的算法[7]和基于特征模板匹配的算法[8-9]等。其检测性能优于ED算法，不需要预知任何先验知识，且不受噪声不确定度影响。但其缺点是需要较多采样点，且运算时间复杂度较高[10]。GOF算法[11-14]将SS转化为一种拟合度检测问题，即假设不存在PU信号时接收信号服从某一特定分布，存在PU信号时接收信号将偏离特定的分布。一般地，假设噪声服从均值为0、方差为σ2的正态分布，SS问题便转化为检验接收信号是否服从均值为0、方差为σ2的正态分布问题。文献[11]和[12]将Kolmogorov-Smirnov(KS)准则、Anderson-Darling(AD)准则和Cramer-vonMises(CM)准则等应用于频谱感知中，且表明GOF算法优于ED算法，但需要知道噪声方差且受噪声不确定度的影响；文献[13]利用特征函数可以完整地描述随机变量这一性质，提出了基于特征函数的盲频谱感知算法(BlindspectrumsensingbasedcharacteristicfunctionandAnderson-Darlingtest)，通过计算接收到的样本经验特征函数与已知特征函数的距离，区分信道中是否存在PU信号。文献[14]将基于特征函数频谱感知算法推广到了多输入多输出系统中。虽然文献[13]和[14]所提算法不需要知道噪声方差，同时克服了噪声不确定度的影响，但是其运算量较大，对SU的计算能力有较高的要求，不适合实时感知。

针对上述缺陷，本文利用PU信号不存在时接收信号的概率密度函数是偶函数这一特征，提出了一种基于二项分布的盲频谱感知算法(BlindspectrumsensingbasedBinomialDistribution，BD)。相较CAD算法，所提算法具有运算量小，感知时间短的优点。而与ED算法相比，所提算法不仅性能明显优于ED算法，不受噪声确定度的影响，而且运算量不高于ED算法，感知时间短。

1信号模型

通常，SS可以表述为一个二元假设检验问题，即存在两种假设：H0表示PU不存在，SU可接入该频谱；H1表示PU存在，SU不可接入该频谱。因此，SS的数学模型[13]可描述为

(1)

(2)

2基于二项分布的盲频谱感知算法(BD)

2.1检验统计量的确定

通常，接收信号xl可以看成遵循某一特定的概率密度曲线(PDF)，因此可以利用H0和H1的PDF的特征差异来区分主用户是否存在。在本文中，笔者利用PDF是否为偶函数这一特征来实现频谱感知。

在H0条件下，根据式(2)可知，接收信号xl服从均值为0，方差为σ2的高斯分布，此时xl的PDF是偶函数[15]。当采样点数足够大时，采样信号的值大于0的个数等于采样信号的值小于0的个数，均为0.5L；在H1条件下，由式(2)可知，接收信号xl服从均值为kσ，方差为σ2的高斯分布，其PDF不再是偶函数。也就是说，当采样点数足够大时，此时采样信号的值大于0的个数不再等于采样信号的值小于0的个数，即采样信号的值大于0的个数不再等于0.5L。

基于上述分析，可以利用采样信号的值大于0的个数是否等于0.5L来判断是否存在PU信号，从而提出BD算法。因此，BD算法的检验统计量T可定义如下

(3)

式中：u(x)表示阶跃函数。显然，SS问题可转化为如下的假设检验问题

(4)

在实际的SS中，T只能通过有限采样点数得到，即

(5)

由于采样点数的有限性，T的实际值与理想值存在一定偏差，即H0时T不能如式(4)那样等于0.5L，而是以PDF的形式呈现。因此，式(4)可重新写为

(6)

于是，BD算法的判决准则可以表示为

式中：γ1和γ2为判决门限。

2.2判决门限的确定及算法步骤

众所周知，在SS中，获取恒虚警概率Pf的判决门限十分重要。一般地，通过给定虚警概率Pf=Pr{T>γ1或T<γ2|H0}获取判决门限γ1和γ2。下面推导通过Pf求判决门限。

u(xl)可以看成一次伯努利试验，试验之间相互独立。因此，检验统计量T可以看作是L重伯努利试验，即

T～B(L,p)

(7)

式中：B表示二项分布；p为xl大于0的概率。基于上述分析可知，H0条件下，p=0.5，此时，T的累积分布函数(CDF)可以表示为

(8)

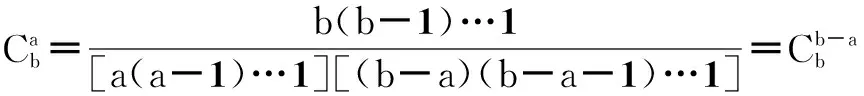
1-F(γ1)+F(γ2)

(9)

因为在H1条件下s=1的概率未知，应保证恒定的Pf，所以双门限γ1和γ2的之间的关系需满足

γ1+γ2=L

(10)

所以，式(8)可以化为

Pf=1-F(γ1)+F(L-γ1)=1-F(L-γ2)+

F(γ2)

(11)

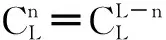
Pf=2-2F(γ1)=2F(γ2)

(12)

于是，检测门限为

γ1=F-1(1-0.5Pf)

(13)

γ2=F-1(0.5Pf)

(14)

综上，本文提出的BD算法可描述如下：

1)对接收信号进行采样，得到采样信号x(k)；

2)由得到的采样信号，通过式(2)得到检验统计量T；

3)给定虚警概率Pf，通过式(9)、(10)得到判决门限；

4)如果T>γ1或者T<γ2，判决H1，否则判决H0。

2.3检测性能分析

根据式(2)可知，在H1条件下，假设s=1的概率为q，当q、信噪比和噪声方差一定时，T的CDF被确定，下面进行Pd的推导。

当s=1和s=-1时，式(7)中p的大小分别为p1和p2。于是，p1，p2可分别表示为

p1=Pr{xl>0|s=1}=1-F1(0)

(15)

p2=Pr{xl>0|s=-1}=1-F2(0)

(16)

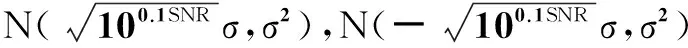
(17)

(18)

由高斯分布的对称性[15]可知p1+p2=1，于是s=1和s=-1时T的CDF分别可以表示为

(19)

(20)

易知

1-FT1(γ1)=FT2(γ2)

(21)

1-FT2(γ1)=FT1(γ2)

(22)

结合式(19)～(22)，BD算法的检测概率可表示为

Pd=Pr{T>γ1orT<γ2|H1}=

FT1(γ2)+FT2(γ2)

(23)

由式(13)、(14)和式(23)可知，BD算法的判决门限和检测概率均与噪声方差无关，这解释了BD算法不受噪声不确定性影响的原因。

3仿真分析

下面在高斯信道下对上述的理论进行仿真验证，并在给定的Pf条件下通过考察本文算法所能达到的检测概率Pd来评价其性能，同时与CAD算法[13]、ED算法[5]性能进行比较。若无特殊说明，仿真中，L=64，虚警概率Pf=0.01，通过式(13)、(14)计算可得门限γ1=42，γ2=22。假设BD算法、CAD算法不知道噪声方差，因为ED算法需要噪声方差，因此假设噪声方差σ2=1。

表1描述了BD算法、ED算法和CAD算法的运算量。从表1可见，BD算法的运算量小于CAD算法。对比于ED算法，虽然BD算法的加法次数比ED算法多L次，但BD算法的乘法次数比ED算法少L次，而乘法比加法复杂，因此BD算法的运算量也小于ED算法。为进一步比较3种算法的运算量，图1给出了不同L情况下，BD算法、CAD算法和ED算法的运算量比较曲线，L由0增加到100。由图1可见，BD算法和ED算法运算量增幅平稳，而CAD算法运算量大幅增加且远大于BD算法。如，采样点个数为80时，BD算法的加法次数和乘法次数分别为159和0，ED算法的加法次数和乘法次数分别为79和80，而CAD算法的加法次数和乘法次数分别为13 117和19 365。此外，虽然BD算法的加法次数比ED算法多L次，但其乘法次数比ED算法少了L次，而乘法的运算复杂度是高于加法的，因此，在L相同情况下，BD算法的运算量略低于ED算法。

表13种算法运算量对比

算法名称加法次数乘法次数ED算法L-1LCAD算法2L2+4L-33L2+2L+5BD算法2L-1无

图1　3种算法运算量比较

图2描述了BD算法、CAD算法和ED算法在不同信噪比下的检测性能。如图2可见，BD算法Pd的理论值与仿真值完全重合，这验证了式(23)的正确性。同时，在相同Pf(Pf=0.01)的前提下，采用BD算法得到的Pd随着信噪比的增大而增大，并在相同信噪比时得到的Pd明显大于ED算法的Pd，略低于CAD算法的Pd，这是因为BD算法只是利用了PDF的部分特征，而CAD算法利用了PDF的全部特征。比如SNR=-5dB时，采用BD算法、CAD算法、ED算法得到的Pd分别为0.883 2、0.925 4、0.255 4。

图2　3种算法性能比较

为了进一步对本文所提算法和ED算法、CAD算法的性能进行比较，图3给出了信噪比为-5dB时3种算法的ROC性能曲线，从图3可见，BD算法比CAD算法的ROC曲线略有下降，但比噪声方差已知时的ED算法性能好。这进一步验证了BD算法的性能明显优于ED算法。

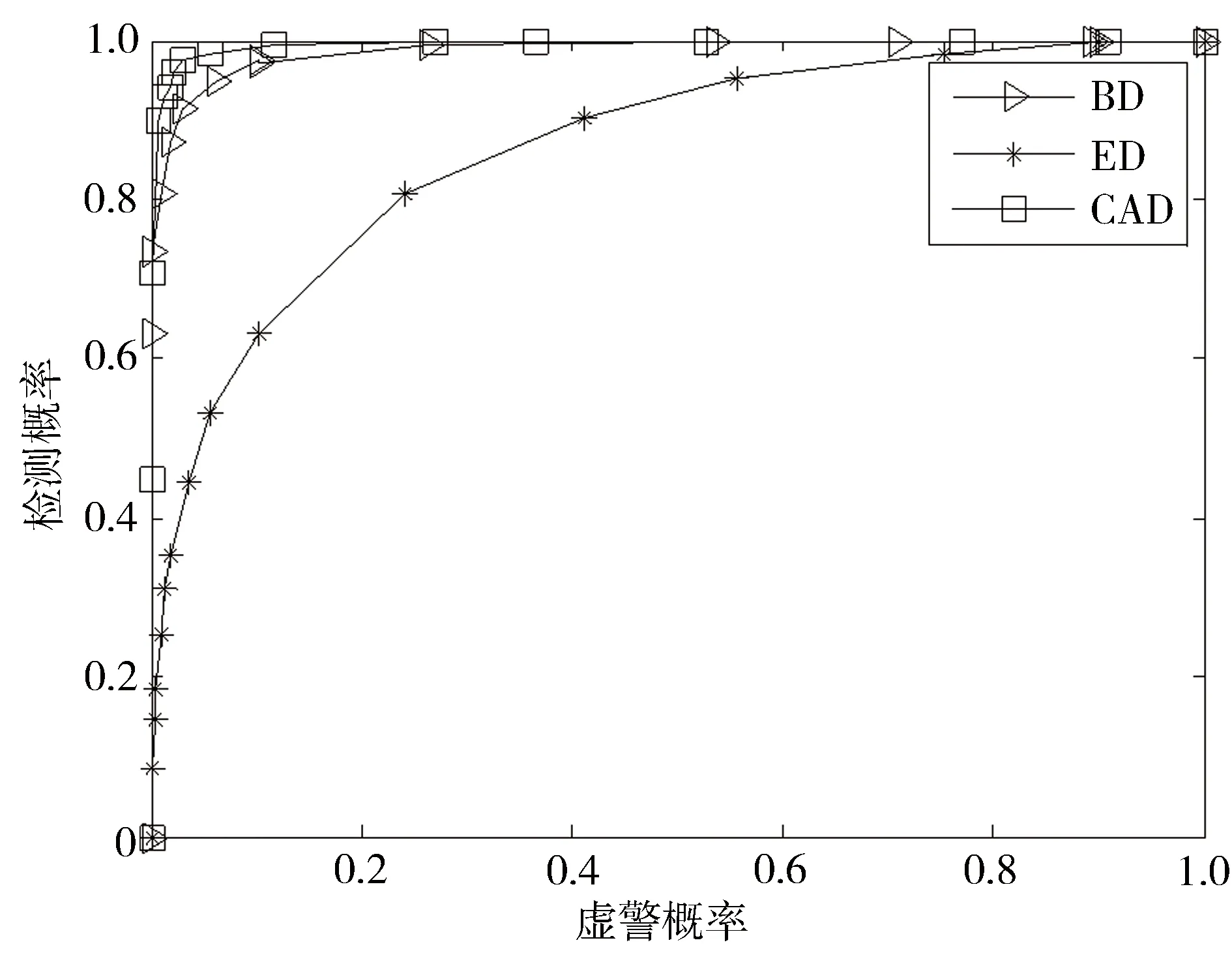
图3　3种算法ROC曲线

4结论

在加性高斯白噪声的环境下，本文利用检验统计量的PDF是否是偶函数这一特征来判断PU是否存在，推导了频谱空闲时检验统计量的概率密度函数，并给出了判决门限的计算方法，从而提出了BD算法。理论分析和仿真表明BD算法的检测性能明显优于ED算法且与CAD算法性能相当，且不受噪声不确定度的影响，重要的是BD算法的运算量明显低于CAD算法且略低于ED算法。

参考文献：

[1]张乃谦，金立标，柴剑平．认知无线电技术在广电中的应用[J]．电视技术， 2012，36(12)：22-24.

[2]MASONTAMT，MZYECEM，NTLATLAPAN.Spectrumdecisionincognitiveradionetworks：Asurvey[J].IEEEcommunicationssurveys&tutorials，2013，15(3)：1088-1107.

[3]YUCEKT，ARSLANH.Asurveyofspectrumsensingalgorithmsforcognitiveradioapplications[J].IEEEcommunicationssurveys&tutorials，2009，11(1)：116-130.

[4]SUTTONPD，NOLANKE，DOYLELE.Cyclostationarysignaturesinpracticalcognitiveradioapplications[J].IEEEjournalonselectedareasincommunications，2008，26(1)：13-24.

[5]TANDRAR，SAHAIA.SNRwallsforsignaldetection[J].IEEEjournalofselectedtopicsinsignalprocessing，2008，2(1)：4-17.

[6]JAINSA，DESHMUKHMM.PerformanceanalysisofenergyandeigenvaluebaseddetectionforspectrumsensinginCognitiveRadionetwork[C]//Proc.InternationalConferenceonPervasiveComputing.Pune：[s.n.]，2015：1-5.

[7]王颖喜，卢光跃.基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报，2010，32(11)：2572-2574.

[8]ZHANGP，QIUR，GUON.Demonstrationofspectrumsensingwithblindlylearnedfeature[J].IEEEcommunicationletters， 2011，15(5)：548-550.

[9]孙宇，卢光跃，弥寅.子空间投影的频谱感知算法研究[J].信号处理，2015，31(4)：83-89.

[10]卢光跃， 弥寅， 包志强， 等.基于特征结构的频谱感知算法[J].西安邮电大学学报，2014， 19(2)：1-12.

[11]WANGH，YANGE，ZHAOZ，etal.Spectrumsensingincognitiveradiousinggoodnessoffittesting[J].IEEEtransactionsonwirelesscommunications，2009，8(11)：5427-5430.

[12]KASHEFSS，AZMIP，SADEGHIH.SpectrumsensingbasedonGoFtestingtechniques[C]//IEEEInternationalConferenceonCommunications.KualaLumpur：[s.n.]，2013：122-127.

[13]沈雷，王海泉，赵知劲，等. 认知无线电中基于拟合优度的频谱盲检测算法研究[J]. 通信学报，2011，32(11)：27-34.

[14]沈雷，陈佩，王海泉，等. 多输入多输出系统基于特征函数频谱盲检测[J]. 电波科学， 2013， 28(6)：1110-1115.

[15]穆德史定华AM，格雷比尔FA.统计学导论[M].史定华,译.北京：科学出版社，1982.

责任编辑：闫雯雯

Fastandblindspectrumsensingbasedonbinomialdistribution

SUHang，YEYinghui，LUGuangyue

(National Engineering Laboratory for Wireless Security， Xi’an University of Posts and Telecommunications， Xi’an 710121， China)

Abstract:The performance of the existing blind spectrum sensing algorithm based on characteristic function and Anderson-Darling test(CAD) is excellent， however， with heavily computation. In this paper， the sample feature is employed as the test statistic to sense the available spectrum for the cognitive users and a blind and fast spectrum sensing based on binomial distribution is proposed. The probability density functions(PDF) of test statistic under free of frequency channel is derived and then theoretical threshold is given. Finally， with comparison to CAD algorithm， analysis and numerical simulations show the proposed algorithm has almost comparable performances and low computation apparently.

Key words:computation；fast and blind spectrum sensing； binomial distribution； sample feature

中图分类号：TP391

文献标志码:A

DOI：10.16280/j.videoe.2016.04.020

基金项目：国家自然科学基金项目(61271276；61301091)；陕西省自然科学基金项目(2014JM8299)

收稿日期：2015-09-21

文献引用格式：苏杭，叶迎晖，卢光跃.基于二项分布的快速盲频谱感知算法[J].电视技术，2016，40(4)：96-100.

SUH，YEYH，LUGY.Fastandblindspectrumsensingbasedonbinomialdistribution[J].Videoengineering，2016，40(4)：96-100.