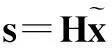多元LDPC码Min-max自适应译码算法

陈紫强,杜婉莹,谢跃雷

(桂林电子科技大学 无线宽带通信与信号处理省部重点实验室，广西 桂林 541004)

多元LDPC码Min-max自适应译码算法

陈紫强,杜婉莹,谢跃雷

(桂林电子科技大学 无线宽带通信与信号处理省部重点实验室，广西 桂林 541004)

摘要:为了降低多元低密度奇偶校验(Low-density parity check，LDPC)码Min-max译码算法的运算量，提出一种自适应Min-max(Adaptive Min-max，AMM)译码算法。该方法以Min-max算法为基础，以每次迭代后的校验节点错误率(Check-node Error Rate，CER)为调节参数，采用自适应算法对变量节点的向量长度进行截短，去除置信度较低的分量，仅对置信度较高的分量进行更新。当CER降低到一定程度时，对校验节点个数进行自适应截短，仅对不满足校验方程的校验节点进行消息迭代更新，进一步降低AMM算法的复杂度。仿真结果表明，在相同误码性能条件下，AMM算法运算量较固定长度截短的Min-max算法减少20%。

关键词:多元LDPC；Min-max；自适应截短；校验节点错误率

为了进一步降低Min-max算法复杂度，本文提出一种多元LDPC码Min-max(AdaptiveMin-max，AMM)自适应译码算法。在每次迭代过程中，以校验节点错误率(Check-nodeErrorRate，CER)为调节参数，对每个节点的LLR向量长度进行自适应截短。当校验节点错误率降低到一定程度时，停止更新已经满足校验关系的节点消息，仅对错误的节点进行后续迭代更新，进一步降低AMM算法的整体复杂度。

1Min-max译码算法

Min-max算法将EMS译码算法[6]中加法运算替换为求最大值运算，降低了硬件实现的复杂度，便于工程应用。AMM算法以Min-max算法为基础，通过自适应截短消息概率向量长度、自适应截短校验节点更新数量两种处理方法，降低Min-max译码算法的译码复杂度。因此，本文首先简要介绍Min-max算法实现流程。

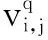
1)初始化

γj(a)=log(Pr(xj=sj)/Pr(xj=a))，

vi,j(a)=γj(a)

(1)

式中：sj代表xj中最大概率的取值。在Min-max译码算法中，初始化步骤前须对参与译码的消息概率向量进行降序排序，并选取消息概率较大的前Nm项作为译码过程中的初始消息。

2)置换步骤

将变量节点索引值vq与校验矩阵H相应位置的取值相乘，得到置换之后的索引值矩阵v′q，即

(2)

式中：a=hi,j(×)b，0≤hi,j,a,b≤q-1，符号“(×)”表示GF(q)域上的乘法。

3)校验节点更新

(3)

其中 a∈{0,1，…,q-1}。

4)逆置换步骤

(4)

式中：a=b(/)hi,j，0≤hi,j,a,b≤q-1。符号“(/)”表示GF(q)域上除法。

5)变量节点更新

(5)

(6)

vi,j(a)=vi,j(a)-x

(7)

变量节点更新中，为了防止式(5)中加法运算结果溢出，对每次变量节点更新运算后进行归一化处理，对其减去运算结果中最小值，如式(7)所示。

6)后验信息计算

(8)

2AMM译码算法

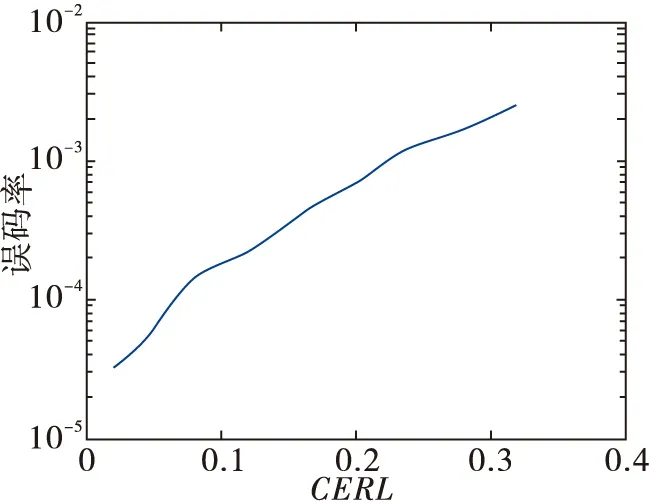
当Min-max算法能够正确译码时，随着迭代次数的增加，消息概率向量的数值会越来越集中到可能性较大的前l项(l

图1　译码中CER与BER关系

鉴于此，提出了多元LDPC码AMM算法，在译码过程中引入CER作为调节因子，第一步自适应地选取下一次迭代过程中译码的消息概率向量的截短长度，仅更新节点向量中置信度较高的分量；第二步自适应截短校验节点更新数量，当校验节点错误率降低到一定程度时，提前结束已经正确的校验节点的更新，仅对不满足校验条件的节点进行后续消息迭代更新。图2给出了AMM算法的算法流程图。

图2　AMM算法流程图

2.1自适应截短节点向量长度

每次迭代结束后，AMM算法需根据当前CER的变化对消息LLR向量长度进行截短。设第i次迭代时，CER值为CERi，AMM算法中消息LLR向量截短为ti。对Min-max算法增加步骤7)，每次完成迭代更新后，计算当前CER的变化率即ΔCERi=CERi-CERi-1，再根据ΔCERi的大小自适应修正下一次迭代消息LLR向量长度ti+1。随着迭代译码的进行，正确的消息越来越集中到消息LLR向量较小的前几项(对应概率值较大项)中，排列靠后的项对译码结果贡献不大，因此迭代中所需要的消息LLR向量可进行逐步的截短。将ti+1与ΔCERi之间的关系用如下的线性函数表示，即

ti+1=「ti+C×ΔCERi⎤=

「ti+C×(CERi-CERi-1)⎤

(9)

式中：t1表示首次迭代所截短消息LLR向量长度，记为A；C表示消息LLR向量长度随着ΔCER的变化速度；「·⎤表示向上取整。A与C的取值大小决定了AMM算法的译码性能和运算复杂度，因此需要通过实验找出误码性能与运算复杂度折中的A与C的值。AMM译码算法步骤7)可分解为：

2)计算CERi，即s中非零值比例。

3)ti+1=「ti+C×ΔCERi⎤。

2.2自适应截短节点更新数量

在AMM算法中，随着迭代次数增加，误码率逐次下降，不满足校验关系的节点数越来越少。此时提前结束已正确的校验节点消息更新，则在后续译码过程中仅需要对错误的节点信息进行更新。可通过减少参与译码的校验节点数量来降低译码复杂度。当译码迭代次数较大时，大部分校验节点已经获得正确译码消息，减少这些节点消息更新对误码性能影响不大。将上述处理过程记为步骤8)。设CERL为校验节点数量截短操作的临界值，AMM译码算法步骤8)可分解为：

1)比较CERi与CERL大小，若CERi≤CERL，跳至2)；否则跳至3)。

2)找出伴随式s中非零值所在位置，记为M；跳至步骤2)对校验矩阵H中M所对应校验节点和与其相邻的变量节点进行迭代更新。

3)跳至步骤2)对校验矩阵H中的所有节点进行译码。

3仿真结果分析

AMM算法中的误码性能和译码复杂度由A值、C值和CERL值这3个参数决定。下面通过实验仿真确定A、C值以及CERL，再对AMM算法和Min-max算法的运算量进行比较。仿真条件如下：信道条件为高斯白噪声(AWGN)信道，调制方式为16QAM调制；采用GF(16)域上码率为0.5，码长为1 056，PEG(ProgressiveEdgeGrowth)构造下NB-LDPC码，码元度分布为λ(x)=0.458 3x3+0.333 4x4+0.208 3x7；仿真时最小帧数设为1 000帧，最小错误帧数设为20帧，最大迭代次数设为12，信噪比设为5dB。

3.1A、C参数选取

图3给出了A、C取不同值情况下AMM算法的误码性能。

图3　AMM算法误码率

图3可以看出，AMM算法的误码率随着C值增加而增加，随着A值增加而下降。当A值为14、15时，AMM算法的误码性能达到了10-5。AMM算法在每次迭代中的消息LLR向量长度值ti随着ΔCERi的值动态变化，采用ti的加权平均值tv作为分析该算法译码复杂度的因子。tv取值越小译码复杂度越低。参数A与C的值决定了tv的取值，同时也影响着AMM算法的性能。将图3中误码率接近10-5时，AMM算法中A与C的值列出，如表1所示。

表1误码率为10-5时A，C，tv以及BER对比情况

A,C15,815,915,1014,815,1114,915,1214,10tv10.56410.1439.6559.3849.2489.1258.9928.887BER1.218×10-52.083×10-52.535×10-53.409×10-53.788×10-54.380×10-55.523×10-55.924×10-5

表1可以看出，tv越大AMM算法的误码性能越好。而tv越小所对应的运算复杂度越低。因此综合考虑误码性能和复杂度，在以下仿真中AMM算法A选定为14，C选定为10。

3.2CERL参数选取

在AMM算法中，随着迭代次数的增加，译码判决后CER越来越小。当CER的值小于临界值CERL时，自适应减少迭代中校验节点数量。图4给出了CER下降到CERL后，AMM算法平均每帧所需要的运算量。

图4　CERL不同值下的每帧平均运算量

由图4可知，临界值CERL在一定程度上影响着迭代译码过程中AMM算法的整体运算复杂度，可以看出CERL越大AMM算法的运算量越小。通过实验仿真，结合误码性能选取合适的CERL取值。下面对CERL取不同值时AMM译码算法的误码性能进行分析，仿真结果如图5所示。

图5　不同CERL值下AMM算法误码率

图5可以看出，AMM算法的误码性能随着CERL增大而变差，当CERL≤1,取10-2数量级时误码达到10-5数量级。这是因为在译码过程中，当大部分码字都译码正确(对应CER较小)时，减少译码节点数量才不会影响到算法的整体误码性能，因此CERL的取值不宜过大。由图4中可知，CERL越大AMM算法运算复杂度越低。综合考虑误码率 (10-5数量级)和译码复杂度，在AMM算法中，CERL值选取为0.04可以获得误码率和译码复杂度的折中。

3.3AMM算法复杂度改进

由于AMM译码算法中采用了CER作为调节参数，减少译码过程中参与运算的节点数量，平均消息向量的截短长度tv不能精确地反应该算法相对于Min-max算法的改进程度。因此，本文对两种算法译码过程中每帧的平均运算量进行统计。为了对比AMM算法相对于Min-max的复杂度优化情况，对这两种算法在相同实验条件下进行仿真，并对二者误码率大致相同条件下的算法运算量的进行对比，将AMM算法、Min-max算法每帧的平均运算量分别记为N1、N2，对比结果如表2所示。

表2Min-max算法与AMM算法复杂度对比

条件误码率AMMMin-maxN1N2N1/N2条件13.2197×10-53.0384×10-57999711079972.20%条件24.7348×10-54.7602×10-5759569666278.58%条件31.4394×10-41.1932×10-4711598950179.51%条件42.2159×10-42.3485×10-4680438387881.12%

表2中给出了AMM算法和Min-max算法在4种误码率大致相同情况下运算量对比，其中前两种情况下，两种算法的误码率达到10-5数量级；第3、4种情况下，两种算法的误码率达到了10-4数量级。综合4种误码率相同情况下运算量的对比可以看出，与Min-max译码算法相比，在相同的误码性能条件下，AMM译码算法运算量降低了大约20%。

4总结

本文提出了一种低译码复杂度的多元LDPC码AMM译码算法。在译码迭代过程中，以校验节点错误率为调节参数，自适应地截短参与运算的消息概率向量长度，在确保一定误码性能的前提下尽可能降低运算量；同时当校验节点错误率下降到一定程度时，停止对满足校验关系的节点更新，通过减少参与消息更新的校验节点数量进一步降低AMM算法复杂度。仿真结果验证了本文方法的有效性。

参考文献：

[1]GALLAGERR.Low-densityparity-checkcodes[J].IREtransactionsoninformationtheory, 1962, 8(1): 21-28.

[2]DAVEYMC,MACKAYD.Low-densityparitycheckcodesoverGF(q)[J].IEEEcommunicationsletters, 1998, 2(6): 165-167.

[3]MACKAYDJ.Gooderror-correctingcodesbasedonverysparsematrices[J].IEEEtransactionsoninformationtheory, 1999, 45(2): 399-431.

[4]WYMEERSCHH,STEENDAMH,MOENECLAEYM.Log-domaindecodingofLDPCcodesoverGF(q)[C]//Proc. 2004IEEEInternationalConferenceonCommunications. [S.l.]：IEEE，2004:772-776.

[5]DECLERCQD,FOSSORIERM.Extendedmin-sumalgorithmfordecodingLDPCcodesoverGF(q)[C]//Proc. 2005InternationalSymposiumontheInformationTheory. [S.l.]：ISIT，2005:1015-1018.

[6]DECLERCQD,FOSSORIERM.DecodingalgorithmsfornonbinaryLDPCcodesoverGF[J].IEEEtransactionsoncommunications, 2007, 55(4): 633-643.

[7]GUANXuan,FEIYunsi.AdaptiveExtendedMin-SumAlgorithmforNonbinaryLDPCDecoding[C]//Proc.GlobalTelecommunicationsConference(GLOBECOM2011).Houston，TX，US：IEEE, 2011：1-6.

[8]SAVINV.Min-maxdecodingfornonbinaryLDPCcodes[C]//Proc. 2008IEEEInternationalSymposiumonInformationTheory.Toronto：IEEE，2008：960-964.

[9]ZHANGX,CAIF,LINS.Low-complexityreliability-basedmessage-passingdecoderarchitecturesfornon-binaryLDPCcodes[J].IEEEtransactionsonverylargescaleintegration(VLSI)systems, 2012, 20(11): 1938-1950.

[10]LINJ,YANZY.Efficientshuffleddecoderarchitecturefornonbinaryquasi-cyclicLDPCcodes[J].IEEEtransactionsonverylargescaleintegration(VLSI)systems, 2013, 21(9): 1756-1761.

[11]LINJ,YANZY.Adecodingalgorithmwithreducedcomplexityfornon-binaryLDPCcodesoverlargefields[C]//Proc. 2013IEEEInternationalSymposiumonCircuitsandSystems(ISCAS). [S.l.]：IEEE，2013：1688-1691.

[12]YANGL,LIUF,LIH.Min-maxdecodingfornon-binaryLDPCcodes[C]//Proc. 2012InternationalConferenceonInformationTechnologyandSoftwareEngineering. [S.l.]：IEEE，2012，108-112.

[13]杨威, 张为. 一种基于分层译码和Min-max的多进制LDPC码译码算法[J]. 电子与信息学报, 2013, 35(7): 1677-1681.

[14]GARCIA-HERREROF,ERBAOL,DECLERCQD,etal.Multiple-Votesymbol-flippingdecoderfornonbinaryLDPCcodes[J].IEEEtransactionsonverylargescaleintegration(VLSI)systems, 2014, 22(11): 2256-2267.

[15]LACRUZJO,GARCIA-HERREROF,VALLSJ.ReductionofcomplexityfornonbinaryLDPCdecoderswithcompressedmessages[J].IEEEtransactionsonverylargescaleintegration(VLSI)systems, 2015,23(11): 2676-2679.

[16]LUYC,GUIFENT,GOTOS.Anefficientdecoderarchitectureforcyclicnon-binaryLDPCcodes[C]//Proc. 2014IEEEInternationalSymposiumonCircuitsandSystems(ISCAS).MelbourneVIC：IEEE，2014：397-400.

[17]LACRUZJO,GARCIA-HERREROF,VALLSJ,etal.Oneminimumonlytrellisdecoderfornon-binarylow-densityparity-checkcodes[J].IEEEtransactionsoncircuitsandsystemsI:regularpapers, 2015, 62(1): 177-184.

陈紫强 (1973— )，副教授，硕士生导师，主研信道编码、协作通信；

杜婉莹 (1991— )，女，硕士生，主研信道编码；

谢跃雷 (1975— )，副教授，硕士生导师，主研通信信号处理、阵列信号处理。

责任编辑：薛京

AdaptiveMin-maxalgorithmfornon-binaryLDPCdecoding

CHENZiqiang,DUWanying,XIEYuelei

(Key Laboratory of Wireless Wideband Communication and Signal Processing, Guilin University of Electronic Technology, Guangxi Guilin 541004, China)

Abstract:In this paper, an adaptive Min-max(AMM)algorithm for non-binary LDPC decoding is proposed to reduce the computational complexity of the Min-max decoding algorithm. Using the error rate of check-nodes as an adjusting parameter to truncate the message vector in decoding iteration adaptively, the computation complexity of AMM algorithm is greatly reduced with little performance loss. When the error rate of check-nodes decreases to a certain small value, stop updating the messages of the correct checked nodes. By reducing the number of nodes participated in updating adaptively, the computation complexity of AMM algorithm is further reduced. The simulation results show that the computation complexity of AMM algorithm is reduced by 20% compared with the fixed message truncation Min-max algorithm given the same bit error rate.

Key words:non-binary low density parity check codes; Min-max; adaptive truncation; check-node error rate

中图分类号：TN911.22

文献标志码：A

DOI：10.16280/j.videoe.2016.04.018

基金项目：国家自然科学基金项目(61451015;61371186;61261032;41201479);广西自然基金项目(2013GXNSFFA019004；2014JJ70068);广西教育厅重点项目(ZD2014052)

作者简介：

收稿日期：2015-08-27

文献引用格式：陈紫强,杜婉莹,谢跃雷.多元LDPC码Min-max自适应译码算法[J].电视技术，2016，40(4)：85-89.

CHENZQ,DUWY,XIEYL.AdaptiveMin-maxalgorithmfornon-binaryLDPCdecoding[J].Videoengineering，2016，40(4)：85-89.