基于相关系数的多天线协作频谱盲检测

叶迎晖，卢光跃

(西安邮电大学 无线网络安全技术国家工程实验室，陕西 西安 710121)

基于相关系数的多天线协作频谱盲检测

叶迎晖，卢光跃

(西安邮电大学 无线网络安全技术国家工程实验室，陕西 西安 710121)

摘要:多天线系统由于可以提高频谱感知可靠性而被广泛应用于认知无线电中。提出了一种适用于多天线系统的盲频谱检测方法。首先，计算不同天线间接收信号的相关系数；其次，对相关系数做适当的变换使其服从学生分布；最后取变换之后的相关系数的均值作为检验统计量，并推导了其判决门限。理论分析和仿真表明，与噪声方差已知的能量检测(ED)以及基于最大最小特征值之比的频谱盲检测算法(MME)相比，所提算法具有更好的检测性能。

关键词:多天线；频谱感知；相关系数；学生分布

认知无线电(CognitiveRadio，CR)[1-2]是一种动态频谱管理技术，旨在解决当前频谱利用率不高的问题，其核心思想是通过频谱感知(SpectrumSensing，SS)发现“频谱空洞”，并合理利用空闲频谱。可见，SS是CR的前提和基础，次用户(SensingUser，SU)必须实时监测频谱变化并能够可靠地检测“频谱空洞”，从而避免对主用户(PrimaryUser，PU)通信造成干扰。

目前，常见的频谱感知方法有能量检测算法(ED)，匹配滤波器检测算法，循环平稳特征检测算法和拟合优度检测算法。其中匹配滤波器检测[1]在加性高斯白噪声环境下性能最优，但其同步要求较高，且必须预知PU发射机信号的先验知识(如信号波形、调制方式等)，限制了算法的应用范围；循环平稳特征检测算法[3]利用通信信号本身具有的循环周期特性来检测授权用户的存在性，不需要预知授权用户信号的先验知识，检测性能较好，缺点是计算较复杂，需要更长的检测时间，降低了系统的灵敏度；能量检测[4-5]算法是最常见的算法，实现简单且不需要知道PU的任何先验信息，但需要知道噪声方差且受噪声不确定度的影响；拟合优度检测算法[6-7]具有较好的感知性能，但其要求感知期间PU信号保持不变，只能在基带进行感知并且信道为高斯信道或慢衰落信道，这限制了其应用范围。

近年来，基于接收信号协方差矩阵特征值分解的盲感知算法也被学者们所关注，比如最大最小特征值之比(MME)[8]，最大特征值与迹之比的方法(MET)[9]，最大最小特征值之差(DMM)[10]。上面的算法都不需要知道噪声方差以及不受噪声不确定度的影响，但存在判决门限不准确以及复杂度高等缺点。

针对上述缺点，利用相关系数的特性提出了认知无线电中基于相关系数的多天线协作盲检测算法，所提算法不需要知道任何先验信息且不受噪声不确定度的影响，同时，可以通过计算得到精度较高的门限值，从而克服了现有算法的弊端。

1认知无线电中基于相关系数的多天线协作盲检测算法

1.1信号模型

通常，频谱感知可以表述为一个二元假设检验问题[11]，即存在两种假设：H0表示主用户不存在，频段空闲，认知用户可接入该频段；H1表示主用户存在，频段被占用，认知用户不可接入该频段。因此，在一个等距阵列天线中，频谱感知的数学模型为

(1)

式中:xi(n)表示第i(i=1，2，…，L)根天线在第n个时刻采样到的信号；s(n)表示PU发射机信号；h表示信道增益；wi(n)表示均值为零、方差为σ2的独立同分布加性高斯白噪声。在实际的通信系统中，传输的PU信号一般是复数，但复数可以表示成实部和虚部的和，如果把实部与虚部分别来考虑，则可以假设s(n)为实数。并且在下文中，始终在实数范围内来考虑问题。同时，为了简便，假设 h=1。

1.2检验统计量的确定

定义第i根天线和第j根天线接收信号的相关系数[12]

(2)

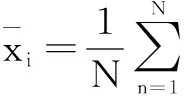
当PU信号不存在时，接收端任意一根天线接收到的信号为均值为0、方差为σ2的高斯白噪声，此时天线之间接收信号是相互统计独立的，在高斯分布中，独立和不相关性是等价的，因此，当采样点N趋于无穷大时，ρi，j=0;当PU信号存在时，天线之间接收信号由于存在PU信号而存在一定的相关性，此时，随着信噪比的增大，其相关系数也增大(ρi，j为正相关)，因此，当采样点N趋于无穷大时，ρi，j>0，即

(3)

但是，H0时ρi，j=0是在采样点数趋于无穷大时得到的值，然而，在实际频谱感知过程中，由于感知时间是有限的，ρi，j只能通过有限个样本点计算得到，即在H0时ρi，j近似等于0。因此，H0时ρi，j的实际值和理想值也会有一定的偏差，也就是说，ρi，j不会与式(3)一样等于0，而是服从某一概率密度函数。根据文献[12]第121页可知，H0在有限个采样点数的情况下，对ρi，j作了适当变换之后服从自由度为N-2的学生分布，即

(4)

为方便描述，定义如下

(5)

根据前面所分析，对于L根天线，可以得到M=L(L-1)/2个不同的ρi，j，因此，也可以得到M个βi，j。

等增益合并是数据融合中一种有效的方法，因此，取βi，j的均值作为检验统计量T，即

(6)

于是，基于相关系数的多天线协作盲检测算法的判决准则可以描述为

(7)

其中，γ为判决门限。

1.3判决门限确定

众所周知，在SS中，获取能够保持恒虚警概率的判决门限是频谱感知算法中关键技术之一。一般的，确定判决门限的方法有两种。一种方法是采用计算机数值仿真法(比如MATLAB仿真等)，当通信系统的参数(如采样点数等)发生了改变，需要重新进行计算机数值仿真产生新的判决门限，因此此种方法不太适合CR系统；第二种方法就是获取恒虚警判决门限的理论表达式，此种方法计算简单，比较适合实际的CR系统。因此，本小节在上一小节的基础上推导确定判决门限的公式。

基于上述分析可知，H0时检验统计量T是M个服从自由度为N-2的学生分布的均值。根据文献[11]可知，当自由度N-2趋于无穷时，学生分布可以近似为标准正态分布，因此，当N趋于无穷时，检验统计量服从均值为0，方差为1/M的高斯分布，因此H0时T的概率密度可以描述为

(8)

此时，虚警概率Pf可描述为

Pf=Pr{T>γ|H0}=1-Pr{T≤γ|H0}=1-F(γ)

(9)

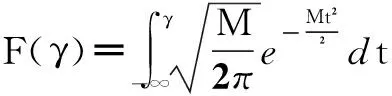
因此，判决门限γ可描述为

γ=F-1(1-Pf)

(10)

1.4算法步骤

综上，认知无线电中基于相关系数的多天线协作盲检测算法步骤如下：

1)根据式(2)计算ρi，j；

2)根据式(5)、式(6)计算检验统计量T；

3)根据式(10)计算得到判决门限；

4)根据式(7)进行判决。

讨论：1)推导判决门限时假设采样点数N趋于无穷大，而实际的频谱感知中，采样点数是有限的，因此，根据式(10)计算得到的判决门限会有一定的误差(后面的仿真会说明采样点较少时采用式(10)得到判决门限的精度就已经比较高了)。

2)由式(6)、式(10)可知，所提算法的检验统计量仅与接收信号有关，所以所提算法不需要知道任何先验信息(如噪声方差)，这说明了所提算法不受噪声不确定度的影响。

3)所提算法、MME算法、ED算法的复杂度见表1。从表1可知，本文所提算法复杂度高于ED算法，低于MME算法，这是因为MME的复杂度主要来源于相关矩阵和对相关矩阵做特征值分解两个部分(相关矩阵计算复杂度为O(NL2)，特征值分解复杂度为O(L3)；所提算法的复杂度主要来源于协方差矩阵的上三角或下三角(均不包含主对角线)的运算，协方差矩阵的上三角运算的复杂度为O(NL2)；ED算法只需要求得所有采样点的能量之和即可，因此复杂度为O(NL)。因此，本文所提算法复杂度小于MME算法高于ED算法。

2仿真分析

下面在高斯信道下对上述的理论进行仿真验证，并通过考察一定Pf条件下本文算法所能达到的检测

表13种算法运算量对比

算法名称复杂度ED算法O(NL)MME算法O(NL2)+O(L3)本文所提算法O(NL2)

概率Pd来评价其性能，同时与ED算法、MME算法性能进行比较。

图1描述了在天线数L=4时，在不同的采样点数的情况下，采用式(10)计算门限得到的虚警概率和理论虚警概率的关系图。从图1可见，当采样点数N>30时，采用式(10)计算得到的门限进行仿真得到的虚警概率和理论值相差不大，因为虚警概率和门限是一一对应的关系，因此采用式(10)计算得到的理论门限和实际门限相差不大，这也验证了式(10)的正确性。

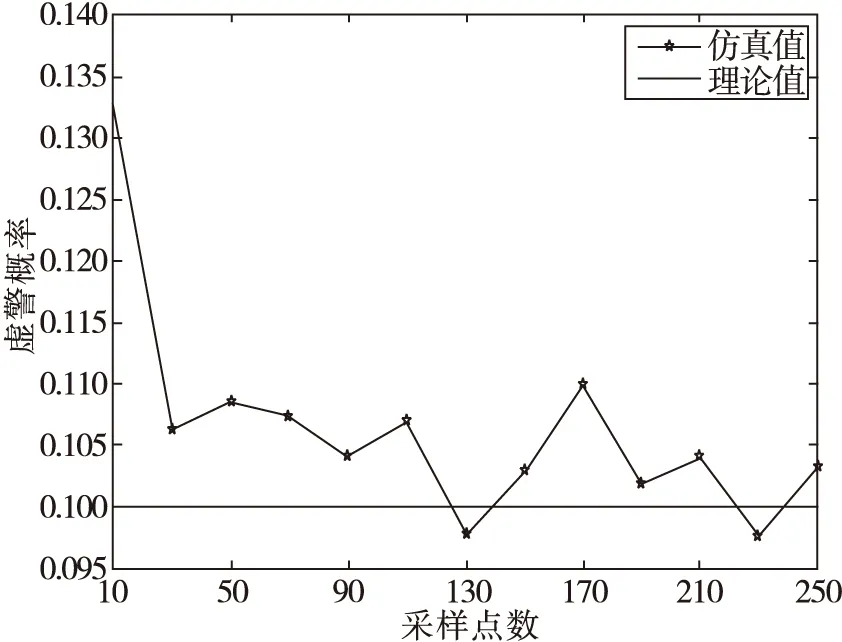
图1　虚警概率的理论值和仿真值

图2描述了在天线数L=4，N=50，虚警概率Pf=0.05时，3种算法的检测性能和信噪比的关系。从图中可知，3种算法的检测性能随着信噪比的增加而增加。在相同信噪比时，本文所提算法明显优于MME算法和噪声方差已知的ED算法。比如在信噪比为-5 dB时，采用本文算法、MME、ED算法得到的检测概率分别为0.99，0.65，0.87。为分析本文所提算法的性能，图3描述了虚警概率Pf=0.05，信噪比为-12 dB时，本文所提算法在不同的天线数L和不同的采样点数N下的检测性能。从图3可见，一方面，在相同天线数时，检测性能随着采样点数的增加而增加；另一方面，在相同采样点数时，检测性能会随着采样点数的增加而增加。

图2　3种算法的检测性能比较图

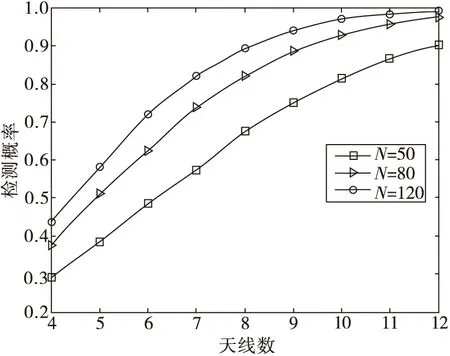
图3　所提算法跟天线数、采样点数的关系图

图4描述了L=6，N=32，信噪比为-10 dB时3种检测算法的工作区间特性(ROC)，从图4可见，本文所提算法的ROC曲线在MME和噪声方法已知的ED算法的ROC曲线上面，这说明了本文算法明显优于MME和噪声方差已知的ED算法。

图4　3种算法的ROC性能曲线

3结论

该文利用样本相关函数的特征，结合等增益合并构造了新的检验统计量，并推导了门限的确定公式，理论分析和仿真表明在较小样本点时采用式(10)计算得到的虚警概率就可以达到较高的精度，所提算法的性能明显优于MME和ED算法，这是由于本文所提算法利用了相关系数的全部特征，即概率密度曲线。与此同时，本文所提算法的复杂小于MME算法。

参考文献：

[1]MASONTA M T，MZYECE M，NTLATLAPA N．Spectrum decision in cognitive radio networks: a survey [J]．IEEE communications surveys & tutorials，2013，15(3)：1088-1107．

[2]HAYKIN S．Cognitive radio：brain-empowered wireless communications[J]．IEEE journal on selected areas in communications，2005，23(2)：201-220．

[3]SUTTON P D，NOLAN K E，DOYLE L E．Cyclostationary signatures in practical cognitive radio applications[J]．IEEE journal on selected areas in communications，2008，26(1)：13-24．

[4]DIGHAM F F，ALOUINI M S，SIMON M K．On the energy detection of unknown signals over fading channels[J]．IEEE transactions on communications，2007，55(1)：21-24．

[5]TANDRA R，SAHAI A．SNR walls for signal detection[J]．IEEE journal of selected topics in signal processing，2008，2(1)：4 -17．

[6]WANG H，YANG E，ZHAO Z，et al．Spectrum sensing in cognitive radio using goodness of fit testing[J]．IEEE transactions on wireless communications，2009，8(11)：5427 -5430．

[7]KASHEF S S，AZMI P，SADEGHI H．Spectrum sensing based on GoF testing techniques[C]//Proc．IEEE International Conference on Communications.Kuala Lumpur：IEEE，2013：122-127．

[8]ZENG Y H， LIANG Y C. Eigenvalue based spectrum sensing algorithms for cognitive radio[J]．IEEE transactions on communication，2009，57，(6)：1784-1793.

[9]ZENG Y H，LIANG Y C， ZHANG R. Blindly combined energy detection for spectrum sensing in cognitive radio[J]．IEEE signal processing letters，2008(15)：649-652.

[10]王颖喜，卢光跃．基于最大最小特征值之差的频谱感知技术研究[J]．电子与信息学报，2010，32(11)：2572-2574．

[11]ANDERSON T W. An introduction to multivariate statistical analysis. 3th edition. wiley-interscience[M]. New Jersey，US：Wiley-Blackwell，2003.

[12]穆德，格雷比尔．统计学导论[M].史定华，译．北京：科学出版社，1982．

Cooperativespectrumsensingbasedoncorrelationcoefficientinmulti-antennacognitiveradio

YEYinghui,LUGuangyue

(National Engineering Laboratory for Wireless Security, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

Abstract:Multiple antennas are widely used in cognitive radio system in that it can improve the spectrum sensing performance. A new cooperative spectrum sensing in multi-antenna cognitive radio is proposed. Firstly, the correlation coefficients between each antenna are calculated. Secondly, the author makes appropriate transformation of every correlation coefficient so as to obey students’ distribution. Finally, a new test is constructed by the use of correlation coefficient’s mean and the theoretical threshold is given. Both analysis and numerical results show that the proposed method outperforms the energy detection(ED) method with noise variance known and the MME method.

Key words:multiple antennas; spectrum sensing; correlation coefficient; students’ distribution

中图分类号：TN92

文献标志码：A

DOI：10.16280/j.videoe.2016.04.014

基金项目：国家自然科学基金项目(61271276；61301091)；陕西省自然科学基金项目(2014JM8299)

作者简介：

叶迎晖(1991— )，硕士生，主要研究方向为认知无线电频谱感知技术；

卢光跃(1971— )，教授，博导，主要研究方向为现代移动通信中信号处理。

责任编辑：许盈

收稿日期：2015-10-14

文献引用格式：叶迎晖，卢光跃. 基于相关系数的多天线协作频谱盲检测[J].电视技术，2016，40(4)：65-68.

YEYH，LUGY.Cooperativespectrumsensingbasedoncorrelationcoefficientinmulti-antennacognitiveradio[J].Videoengineering，2016，40(4)：65-68.