中考成绩与高一学习成绩的回归分析
陈颖
摘 要:利用回归分析对江苏省南通市某中学2005届高一学生的中考成绩和高一学习成绩进行了探讨,发现学生的中考成绩与高一学习成绩之间存在显著的线性关系。这对教学改革是非常有益的。
关键词:回归分析;方差;相关关系;相关系数
【中图分类号】G 【文献标识码】B 【文章编号】1008-1216(2016)01C-0018-03
一、资料的来源以及处理方法
(一)资料的来源与整理
从江苏省南通市某中学查到2005届高一学生的原始资料:中考成绩,高一各门功课的总成绩。以班级为单位,以学号代替学生的真实姓名,将中考成绩从高到低排列名次,再将中考成绩与高一学习成绩排出对照表,进行分析。
因为该校2005届高一学生共5个班252人。本文只选择了4个班总人数205人,占全年级人数的81.35%,其中未选的一个班为美术特色班,因为无可比性而未选。选择的学生均为同一市区中考录取的学生,各班学生均为同一年中考,所以入学时的中考成绩具有可比性;各班同学在高一期间均由相同的老师任教,评卷时的评分标准一致,学生的学习环境也相同,所以高一的学习成绩具有可比性。由于篇幅较长,仅列出一个班级的资料。(见表一)
表一 :(1)班学生入学成绩与高一成绩的对照表
代号 中考成绩 高一成绩 高一名次
1 549 736 3
2 522 725 5
3 522 586 39
4 520 748 1
5 513 709 8
6 513 730 4
7 512 741 2
8 512 713 7
9 508 707 9
10 508 707 10
11 506 716 6
12 506 700 12
13 505 684 14
14 505 706 11
15 505 664 18
16 503 666 17
17 501 685 13
18 501 660 19
19 500 672 16
20 500 658 20
21 500 655 22
22 499 673 15
23 498 656 21
24 498 624 29
25 497 624 30
26 496 654 23
27 495 644 25
28 495 628 28
29 494 649 24
30 493 636 26
31 492 629 27
32 492 570 42
33 491 615 33
34 489 618 31
35 489 604 36
36 488 617 32
37 488 572 41
38 486 575 40
39 486 615 34
40 486 604 37
41 484 560 46
42 484 555 47
43 479 564 44
44 476 564 45
45 475 567 43
46 474 589 38
47 470 586 39
48 470 527 48
49 467 503 49
50 467 495 50
(二)对数据的分析
1.以班级为单位,对学生的中考成绩和高一学习成绩进行相关分析。
2.以年级为单位,对学生的中考成绩和高一学习成绩进行相关分析。
3.对其他问题进行特殊分析。
二、计算结果的处理和分析
(一)班级数据处理
以班级为单位,对学生的中考成绩与高一学习成绩进行研究, X为学生的中考成绩, Y为学生的高一学习成绩。每一个学生的中考成绩和高一学习成绩为一对样本值 ,利用上面的模型,对所得数据进行处理得到:
1.求出拟合方程。
由所给数据求出:
∑XY=15862529,∑X=24809,∑Y=12321985,
X=496.18, Y=637.3
可以求得: = Y-bX=637.7-3.41×496.18=-1054.27
所以拟合出回归方程为: Y=-1054.27+3.41X
2.利用方差检验对回归方程的检验。
回归SS:自由度为1
平方和为
均方:142501.2
残差SS:自由度为:n-2=50-2=48
平方和为:
均方:
校正SS:自由度为:n-1=50-1=49
平方和为:198664.5
(综合各平方差见表二)
表二:方差分析表
来源 自由度 平方和 均方 F—值
回归SS 1 142501.2 142501.2 122.3785
残余SS 48 55892.61 1164.43
全部 49
而经检验F表(1,48,0.90)的值在2.81~2.84之间。
此时的F1=122.3785 > F表(1,48),则认为在显著性水平0.90水平下,Y与X之间有显著的线性关系,即回归方程是显著的。
再次检验F表(1,48,0.99)=7.20,此时F1=122.3785>7.20,则认为在显著性水平0.99下,Y与X之间仍存在显著的线性关系,即回归方程是显著的。
3.利用回归方程的相关系数进行检验。
相关系数
由此也可以推导出相关系数为0.8475是相当高的。同样可以说明中考成绩与高一学习成绩之间的确存在极其显著的线性相关关系。
综上所述,由方差分析表以及相关系数的分析可以看出学生的中考成绩与高一的学习成绩有显著的线性关系。也就是说对这个班来说,入学时成绩好的,高一学习成绩相对而言还是好的。当然也存在个别学生的学习成绩有所退步的现象。
但就全班总体情况而言,特别选出全班前10名同学的高一学习成绩名次变化情况。(见表三)
表三:(1)班中考前10名学生的高一学习成绩及名次变化表
代号 中考成绩 高一成绩 名次
1 549 736 3
2 522 725 5
3 522 586 39
4 520 748 1
5 513 709 8
6 513 730 4
7 512 741 2
8 512 713 7
9 508 707 9
10 508 707 10
表中可以看出1班中仅有3号由原来的第3名下滑到第39名,其他的9个人均保持前10名的位置,占这10人中的90%。9个人中有4个人进步,3个人退步,2个人原地不动。虽然名次上有小小的变动,但总体上几乎都保持在班级的前列。
再看班级后十名同学的成绩名次变化,见表四。
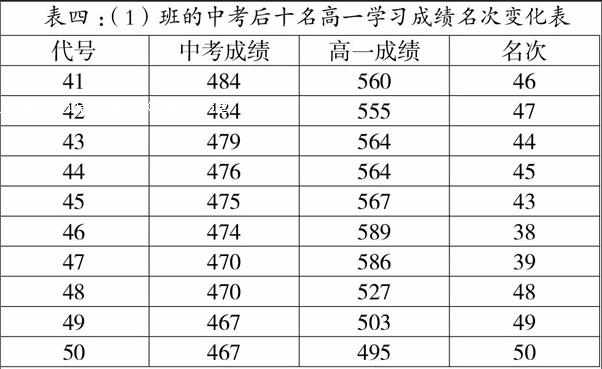
表四:(1)班的中考后十名高一学习成绩名次变化表
代号 中考成绩 高一成绩 名次
41 484 560 46
42 484 555 47
43 479 564 44
44 476 564 45
45 475 567 43
46 474 589 38
47 470 586 39
48 470 527 48
49 467 503 49
50 467 495 50
表中可以看出后十名的同学的名次有所变化,其中3个人进步,4个人退步,还有3个人原地不动。但总体上仍然处于第38名至第50名之间,仍然是处于班级的后列。
就前十名与后十名的成绩及名次变化来看,除了个别同学的成绩有了突飞猛进或有的同学有了大幅度的下滑,大部分的学生入学成绩好的,高一学习成绩仍然是好的;入学时成绩差的,高一学习成绩仍然是差的。
(二)年级数据处理
全年级的中考成绩和高一学习成绩的分析处理:
为了进一步说明中考成绩和高一学习成绩之间的关系,现对整个年级的成绩进行分析。(见表五)
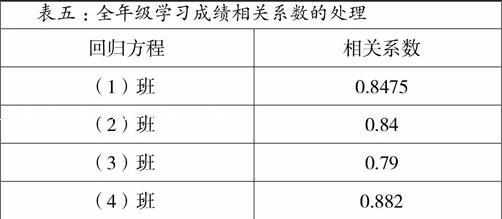
表五:全年级学习成绩相关系数的处理
回归方程 相关系数
(1)班 0.8475
(2)班 0.84
(3)班 0.79
(4)班 0.882
由表五可以看出全年级的中考成绩与高一学习成绩之间存在显著的线性关系,从而进一步的说明高一学习成绩受到中考成绩的影响。中考成绩好的高一学习成绩相对比较好。
(三)全年级学习成绩的预测
由上述的推导过程中可以发现中考成绩与高一学习成绩之间存在显著的线性关系。然而是否能通过中考成绩和回归方程对高一学习成绩进行一个预测呢?我对高一成绩以及拟合值进行了分析,见表六:
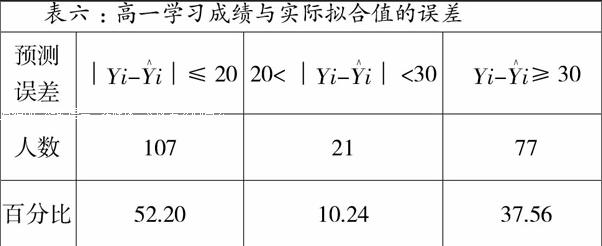
表六 :高一学习成绩与实际拟合值的误差
预测
误差 ││≤20 20<││<30 ≥30
人数 107 21 77
百分比 52.20 10.24 37.56
从表中可以看出,有52.20 %的学生可以预测出的七门的总成绩与实际的总成绩差的绝对值不超过20分,有62.44%的同学预测误差不超过30分。因此,可以利用中考成绩和回归方程预测高一学习成绩。
三、讨论
有人可能认为中考成绩对高一学习成绩有影响,但关系不大。因为初中所学的知识只是为高中的进一步学习打下了基础。然而,通过对南通市某校2005届学生的情况统计分析来看,中考成绩对高一学习成绩来说非常重要,那么,为何会导致这样一种结果呢?
(一)学习成绩是各个阶段学生学习努力的结果
在初中学好了知识,扩展了知识面,为以后高中系统的学习打下了基础。而高中的学习是对初中所学知识的延伸。正如工人盖房子,在原来已经打牢地基的基础上添砖加瓦,总比在原来一无所有的基础上重新布局要省事省力,特别是高一阶段,吃了些初中的“老本”。因此,中考成绩会影响高一学习成绩。
(二)学习习惯与学习方法是影响高中学习的重要因素
良好的学习习惯以及正确的学习方法是决定高中学习成绩的重要因素。这些习惯和方法是在初中学习的过程中逐渐培养起来的。经过三年的学习,成绩好的学生逐渐形成自己的一套学习习惯和学习方法。在高一阶段,学习成绩好的继续延续适应的学习方法。学习成绩较差的学生延续了自己在初中时不尽良好的学习习惯和学习方法,有的虽已经意识到自己的薄弱之处,希望做一些改变,但毕竟学习习惯以及学习方法不是一朝一夕能形成的,所以成绩仍然不理想。但是只要学生继续不断地努力,学习成绩一定会得到提高。
总之,本文涉及的问题比较复杂,还有待于今后进一步做出更全面更深入的探索。
参考文献 :
[1]梁之舜.概率论及数理统计[M].北京:高等教育出版社,1980.
[2]高晶,陆仲伟.高考成绩与大学成绩的回归分析[J].丹东师专学报,1994,(1).
[3]别雪君,李祖超.大学成绩与高考成绩相关关系的统计分析[J].建材高教理论与实践,1997,(4).
[4]韩阔.美术类学生高考成绩与大学学习成绩的相关性研究[J].中国考试,2012,(2).
[5]香红丽,罗淑云.探讨高考成绩和大学阶段学习能力的关系[J].中国科教创新导刊,2010,(28).
[6]谢中才,郑惠娟.大学生高考成绩与大学阶段学习成绩的相关分析[J].数学的实践和认识,2009,(12).
[7]高世泽.高考成绩与大学成绩的关系[J].重庆师范学院学报(自然科学版),1986,(1).

