十字聚焦型微通道内弹状液滴在黏弹性流体中的生成与尺寸预测
张沁丹,付涛涛,朱春英,马友光(天津大学化工学院,化学工程联合国家重点实验室,天津化学化工协同创新中心,天津 300072)
十字聚焦型微通道内弹状液滴在黏弹性流体中的生成与尺寸预测
张沁丹,付涛涛,朱春英,马友光
(天津大学化工学院,化学工程联合国家重点实验室,天津化学化工协同创新中心,天津 300072)
摘要:利用高速摄像仪对十字聚焦微通道内液滴在黏弹性流体中的生成过程进行了实验研究。微通道截面为600 μm×600 μm的正方形结构,采用硅油作为分散相,含0.3%表面活性剂十二烷基硫酸钠(SDS)的聚环氧乙烷(PEO)水溶液(质量分数分别为0.1%,0.3%,0.6%)为连续相。实验观察到了弹状流、滴状流和喷射流3种流型。对弹状流型下液滴生成过程的颈部动力学进行了研究,考察了两相流率、连续相毛细数及弹性数对液滴尺寸的影响。结果表明:弹状液滴尺寸随连续相流率、毛细数及弹性数的增加而减小,随分散相流率的增加而增加,连续相弹性对液滴尺寸的影响相对较小。以油水两相流率比和连续相的毛细数及Reynolds数为变量建立了弹状液滴尺寸的预测关联式,预测值与实验值吻合良好。
关键词:微通道;两相流;流体动力学;液滴;黏弹性;尺寸预测
2015-07-06收到初稿,2015-08-07收到修改稿。
联系人:马友光。第一作者:张沁丹(1991—),女,硕士研究生。
Received date: 2015-07-06.
引 言
微化工技术自20世纪90年代兴起以来,即受到了国内外研究者的广泛关注[1-2]。微通道中的气液两相流及液液两相流是微化工技术的基础,主要研究内容涉及流型、气泡(液滴)的生成动力学及尺寸关联等[3-7]。利用微通道生成的液滴具有均一性强及尺寸可控等优点,在乳化、结晶、萃取、合成等化工过程中具有重要的应用价值[8-10]。目前,针对微通道中液滴生成的研究主要在牛顿流体的液液两相流中开展。Cubaud等[5]研究了十字形微通道中牛顿流体液液两相流中出现的5种流型,并用两相流率和连续相毛细数对液滴尺寸进行了关联和预测。Fu等[6]考察了十字聚焦微通道中液滴的生成过程,研究了滴状流至喷射流的流型转变,同样建立了液滴尺寸的预测模型。
近年来,微通道中两相流的研究方向开始向非牛顿流体发展。Fu等[11]研究了不同尺寸的十字聚焦微通道中气泡在具有剪切变稀性的非牛顿流体中的生成过程,发现非牛顿流体的流变性对气泡生成过程的颈部动力学及气泡尺寸有显著的影响,并建立了气泡尺寸的预测关联式。Steinhaus等[12]研究了不同分子量PEO水溶液的弹性和微通道尺寸对液滴生成的影响,发现当PEO溶液的分子量较大时会表现出较高的弹性和拉伸黏度,分散相细丝增长,颈部破裂所需时间增加。Lee等[13]使用含有甘油的PEO水溶液作为分散相,将表面活性剂加入连续相,系统研究了微通道中分散相细丝的生成过程,发现存在一个受到分散相黏弹性及表面活性剂迁移效应共同作用的稳定区域,这种共同作用会导致分散相细丝的增长,同时可控制微通道中生成液滴的尺寸。
已开展的研究大多集中在气液两相流和将非牛顿流体作为分散相的液液两相流,而将非牛顿流体作为连续相的研究相对较少,亟待深入研究。本文研究了十字聚焦微通道内弹状液滴在具有黏弹性的PEO水溶液中的生成过程,考察了不同因素对液滴尺寸的影响,并提出了液滴尺寸的预测模型。
1 实验部分
实验在截面为600 μm×600 μm(深度×宽度)的十字聚焦型微通道内进行。微通道采用聚甲基丙烯酸甲酯(PMMA)板(45 mm×27.5 mm×2 mm),通过精密铣削制作得到,图1为微通道结构。微量注射泵(PHD 2000,Harvard Apparatus,USA)通过聚乙烯软管(内径为1.02 mm)分别驱动互不相溶的两相流体流入水平放置的微通道内。分散相以体积流率Qd流入主通道,连续相以体积流率Qc/2分别流入与主通道相垂直的两个侧通道,两相流体在十字聚焦微通道的分岔口以错流方式接触。连接着显微放大镜(ECLIPSE Ti-U,Nikon,Japan)的高速摄像仪(i-SPEED CDU,Olympus,UK)实时观测并记录实验数据,拍摄速率为1000 fps。用连着电源(Ti-PS 100 W,Nikon,Japan)的12 V DC卤素灯作为光源,放置在微通道的另一侧,为图像采集提供充足的光线。在每次调节体积流率后,应在液滴生成稳定至少5 min后再采集图像。
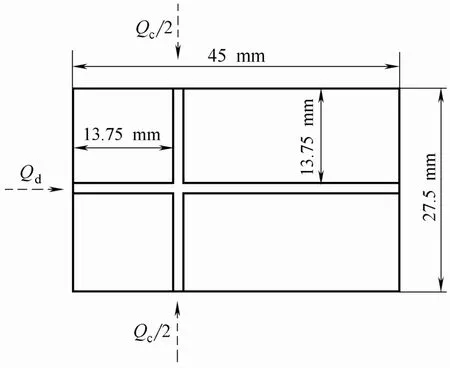
图1 十字聚焦型微通道结构Fig.1 Schematic diagram of flow-focusing microchannel
用硅油作为分散相,具有黏弹性的聚环氧乙烷(PEO)水溶液作为连续相。PEO的分子量MW=1×105,质量分数分别为0.1%、0.3%和0.6%。在PEO水溶液中加入质量分数0.3%的十二烷基硫酸钠(SDS),使得连续相与微通道壁面之间的接触角减小,壁面由疏水性变为亲水性,润湿性增强,以生成稳定的水包油液滴。流体的密度由密度仪(DMA-4500-M,Anton Paar,Austria)测量,两相流体之间的界面张力和接触角均采用表面张力仪(OCAH200,Data Physics instruments GmbH,Germany)通过悬滴法测量。两相流体的各项物性参数见表1。

表1 两相流体物性参数Table 1 Physical properties of experimental fluids
PEO水溶液具有剪切变稀性,其流变性质由扩展流变仪(AR1000,TA,USA)测定。在剪切速率1~1000 s−1的范围内分别测定了3种浓度PEO水溶液的流变性质,如图2所示。
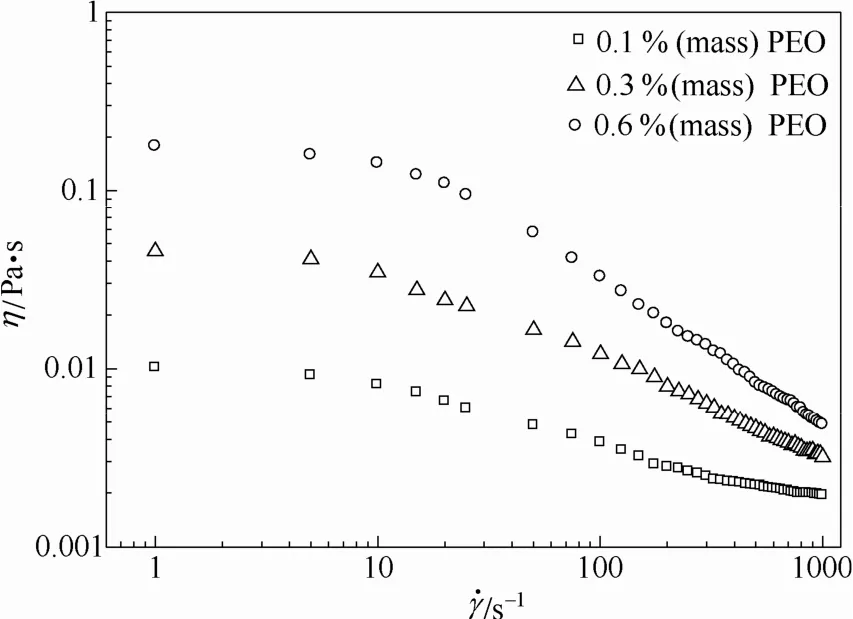
图2 PEO水溶液流变性质Fig.2 Rheological properties of PEO solutions
PEO水溶液的流变性质采用Carreau模型描述[14-15]
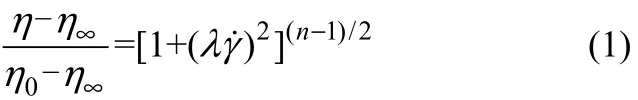
式中,η0和η∞分别表示PEO水溶液的零剪切黏度和无穷剪切黏度。通过实验测定PEO水溶液的η0,近似地认为剪切速率极小时(在本实验中为1 s−1)对应的剪切黏度为η0[16]。η∞取溶剂黏度,在本实验中的溶剂为含0.3% SDS的去离子水,用乌氏毛细管黏度计(iVisc,LAUDA,Germany)测得其黏度为1.01 mPa·s。时间常数λ和流动指数n可以通过回归流变数据得到。PEO水溶液的各项流变参数见表2。所有实验均在293.15 K和常压下进行。
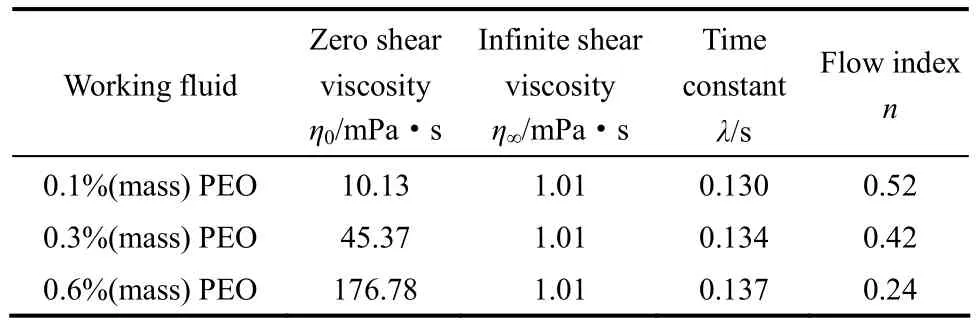
表2 PEO水溶液流变参数Table 2 Rheological parameters of PEO solutions
2 结果与讨论
2.1两相流流型观察
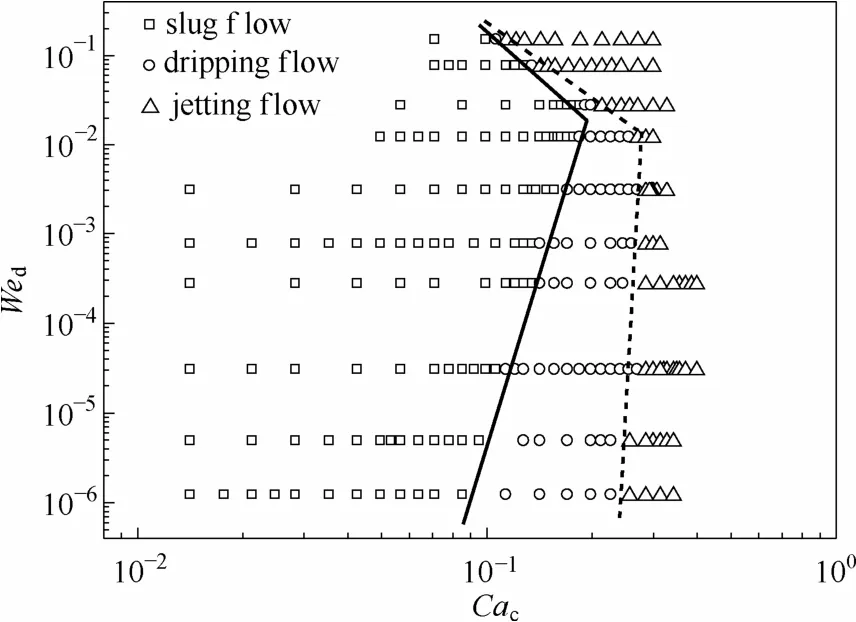
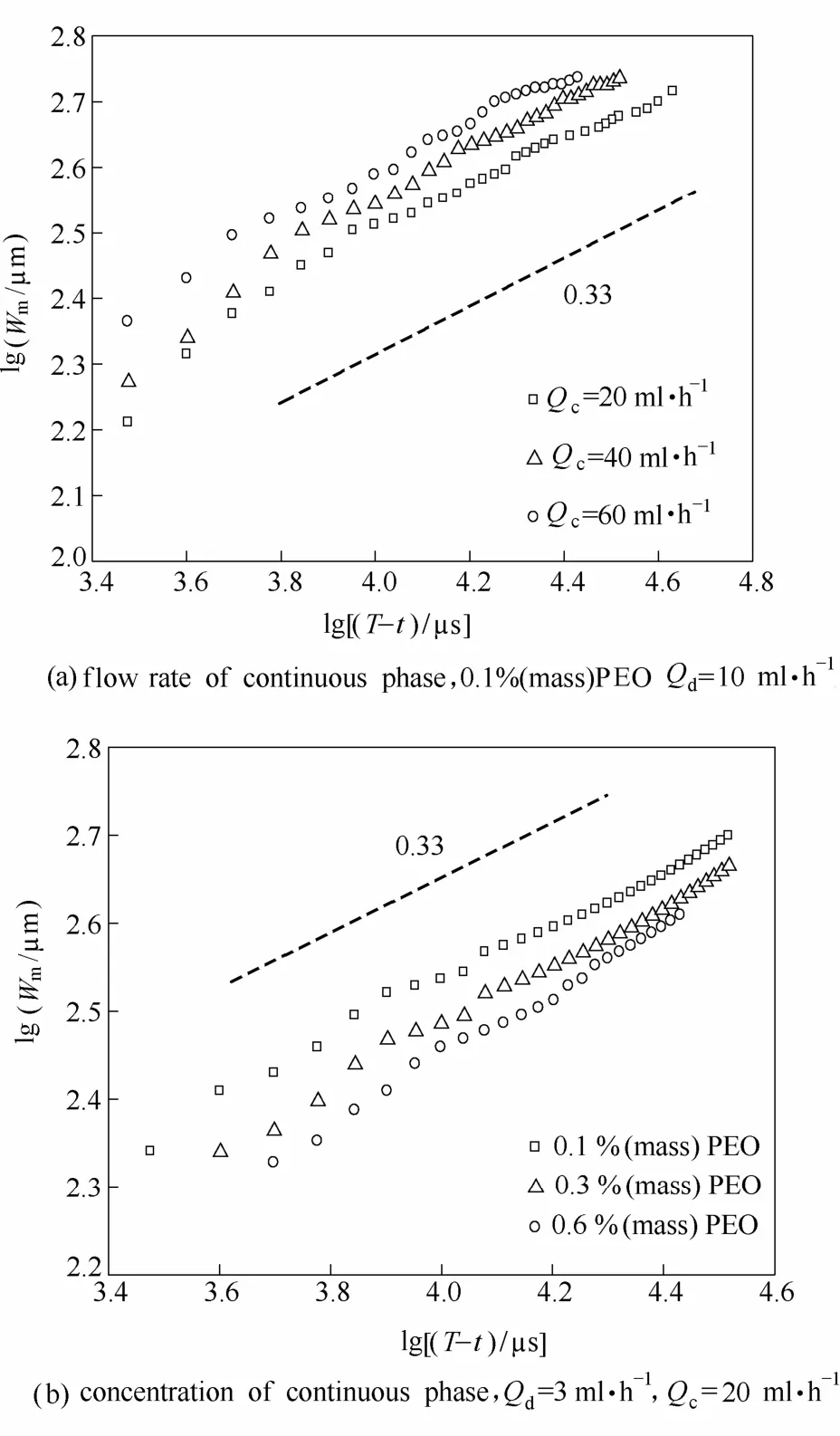
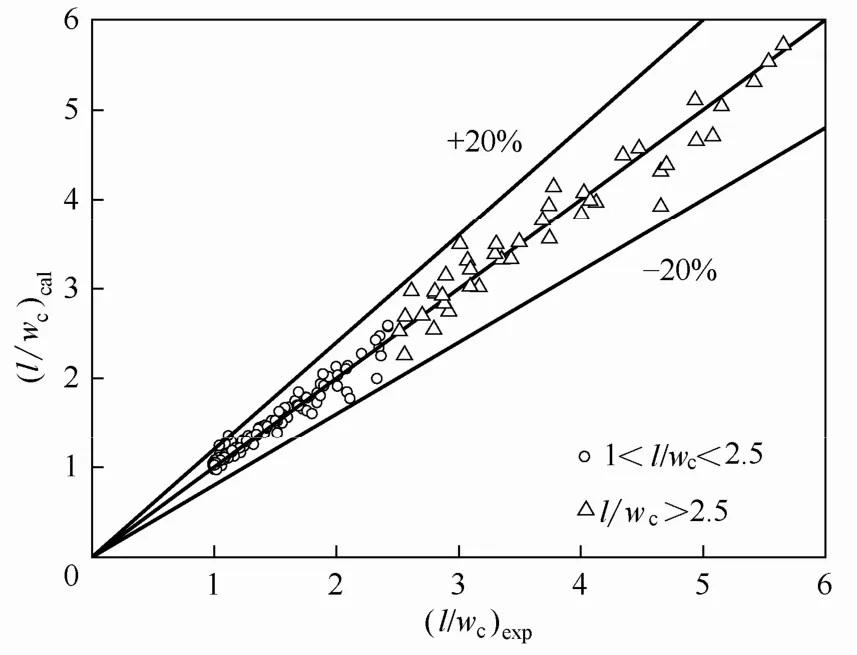
实验过程中,两相流体的流率范围分别为0.2 图3 微通道内硅油-PEO水溶液两相流主要流型Fig.3 Flow pattern of silicone oil-PEO solution in microchannel Qd=50 ml·h−1 毛细数Ca和Weber数We是划分流型的重要参数。Fu等[6]和Ren等[16]分别研究了牛顿流体和非牛顿流体中液滴生成过程的流型及流型转变,均采用表示连续相黏性力与界面张力比值的毛细数Cac和表示分散相惯性力与界面张力比值的Weber数Wed绘制流型图。 式中,ηc,0表示连续相的零剪切黏度,ud与uc分别表示分散相和连续相的速度,σ表示两相流体间的界面张力,ρd表示分散相密度,wc表示微通道宽度。 以Cac与Wed绘制的流型图和各流型之间的转换线如图4所示。当Cac与Wed均较小时,界面张力在液滴的生成过程中占主导作用,形成弹状流。对于相同的Wed值,随着Cac的增大,黏性力逐渐克服界面张力的作用,流型开始由弹状流向滴状流转变,直至出现喷射流,此时连续相的黏性力占主导作用。弹状流至滴状流的流型转变线方程为(Wed>10−2∩Wed=1×10−4Cac−3.2)∪(Wed<10−2∩Wed= 7×107Cac13.2),滴状流至喷射流的流型转变线方程为(Wed>10−2∩Wed=4×10−4Cac−2.8)∪(Wed<10−2∩Wed= 2×1034Cac64.9)。Fu等[6]重点研究了滴状流至喷射流的转变,发现当Cac≥10−2∩Wed≥10−2时流型转变线方程为Wed=7×10−6Cac−1.9。将本实验得到的滴状流至喷射流的流型转变结果与其对比,发现将具有剪切变稀性的非牛顿流体作为连续相更不易形成喷射流。 图4 流型图及流型转换线Fig.4 Flow patterns map and transition lines(solid lines —transition lines from slug to dripping flow; dash lines —transition lines from dripping to jetting flow; dispersed phase is silicone oil, 0.2 在实验条件范围内观察到的3种流型中,弹状流出现的区域较大,是微通道内液液两相流中最普遍出现的流型。同时,弹状液滴在乳化、结晶等操作中的应用十分广泛[9-10],因此本工作将液滴长度大于微通道宽度的弹状液滴作为研究重点,着重研究其生成动力学并提出尺寸预测关联式。 2.2弹状液滴生成动力学 将分散相细丝被夹断的时刻定义为时间零点,考察了弹状液滴在1个周期内的生成动力学,液滴生成过程可分为等待、膨胀、挤压和快速夹断4个阶段。在液滴生成过程中,颈部宽度指的是分散相细丝在膨胀阶段的最大宽度和在挤压及快速夹断阶段的最小宽度。由于微通道的实际尺寸与其在图像中所占的像素点呈正比,通过在画图程序中分别读取颈部宽度和微通道宽度所占的像素点,再结合已知的微通道实际尺寸,即可通过比例计算得到颈部的实际宽度。分散相细丝断裂后,液滴生成首先进入等待阶段[图5(a)和图5(b)],分散相细丝在界面张力的作用下会在轴向经历一个回缩过程,在此阶段中颈部的宽度等于微通道宽度,并且不随时间变化。进入膨胀阶段[图5(c)],连续相在此阶段不断积累能量,分散相细丝在轴向被拉长,在径向不断膨胀,此时的颈部宽度大于微通道宽度并随着时间缓慢增加,直至最大颈部宽度830 μm。在挤压阶段[图5(d)和图5(e)],分散相头部受到微通道限制,此时的连续相已积累了足够的能量,分散相受到两侧连续相流体在轴向的拉伸作用和径向的挤压作用,颈部宽度开始逐渐减小。当颈部宽度小于538 μm时液滴生成进入快速夹断阶段[图5(f)和图5(g)],颈部宽度迅速减小至81 μm,直至断裂生成新的液滴[图5(h)]。图5(i)为液滴在一个生成周期中的颈部宽度Wm随时间变化的过程。 图5 弹状液滴生成过程Fig.5 Slug droplet formation process(a)—(h) dynamics of slug droplet formation in PEO solution; (i) temporal evolution of neck of liquid thread Wm; 0.1% PEO solution, Qd=10 ml·h−1, Qc=20 ml·h−1 微通道内弹状液滴在PEO溶液中的生成过程与Fu等[17-18]研究的十字聚焦微通道内弹状气泡生成过程类似,均由4个阶段组成,其中快速夹断阶段中颈部宽度随时间的变化是重点研究内容。Dollet 等[19]研究了十字聚焦型微通道中气泡的生成动力学,认为在此阶段颈部的断裂受到两相的惯性力而不是界面张力的驱动,并提出了在快速夹断阶段分散相颈部宽度Wm与剩余时间T−t之间的关系满足幂律规律Wm∝(T−t)1/3。 在弹状液滴生成过程中的快速夹断阶段,最小颈部宽度Wm随剩余时间T−t的变化如图6所示。对于不同的连续相流率和浓度,拟合得到的幂指数均为0.33±0.02,与Dollet等[19]的结果相同,说明在分散相颈部断裂前的快速夹断阶段液滴在黏弹性流体中的颈部变化过程与气泡在牛顿流体中相同,均受到两相惯性力驱动。 图6 快速夹断阶段颈部宽度Wm随剩余时间(T−t)的变化Fig.6 Scaling width of thread Wmin function of remaining time (T−t) for pinch off stage 2.3弹状液滴尺寸预测 微通道中生成液滴的尺寸受操作条件(如两相流率、温度、压力)、流体性质(如黏度、表面张力、黏弹性)、微通道(如材质、构型、深宽比)等因素影响。为了考察液滴尺寸与各影响因素之间的关系,将液滴尺寸量纲1化,用液滴长度l与微通道宽度wc的比值l/wc表示弹状液滴的尺寸。实验将分散相流率Qd、连续相流率Qc、油水两相流率比Qd/Qc和连续相毛细数Cac、弹性数El作为考察因素,分别研究了两相流率和连续相的黏度、弹性对弹状液滴长度的影响。弹状液滴长度随不同影响因素的变化如图7所示。 固定分散相流率,随着连续相流率的增加,连续相在微通道分岔口与分散相接触时对其施加的挤压力增大,分散相更容易被夹断生成液滴,液滴的长度减小。当连续相流率一定时,分散相流率增加,连续相需要积累更多的能量以夹断分散相,液滴长度随之增大[图7(a)]。对于相同的连续相毛细数和弹性数,液滴尺寸均随油水两相流率比Qd/Qc增大而增大[图7(b)和图(c)]。 由于连续相具有剪切变稀性,其黏度会随剪切速率增大而减小,因此需要使用不同连续相流率对应的黏度值计算连续相毛细数。根据Carreau模型[14],不同连续相流率对应的黏度值的计算式为 连续相的流率增加,其表观流速增加,黏度减小,由于表观流速的增加幅度远大于黏度的减小幅度,连续相毛细数随连续相流率增加而增大。在两相流率比相同的情况下,连续相毛细数增大,作用在两相界面上的剪切力增大,加速了分散相被夹断的速率,弹状液滴尺寸减小[图7(b)]。 弹状液滴尺寸随弹性数增大而减小[图7(c)]。弹性数El是反映流体弹性力与惯性力相对大小的量纲1准数,用弹性数描述PEO溶液的弹性,其表达式为 式中,λZ为PEO溶液的最长松弛时间。 Tirtaatmadja等[20]通过实验得到了PEO稀溶液(0.01≤c/c*≤1)的有效松弛时间λeff与最长松弛时间λZ之间的关系 将PEO水溶液的浓度量纲1化,用c/c*表示,c*代表溶液的临界交叠浓度,计算方法为 其中,PEO水溶液的本征黏度[η]只与其分子量有关,表达式为 使用有效松弛时间λeff计算PEO溶液的弹性数,可以将溶液浓度对弹性的影响体现在弹性数中。根据式(5)~式(8),PEO溶液的弹性数与其分子量和浓度等参数及微通道尺寸有关,而不受两相流率影响。 如图7(c)所示,不同浓度PEO水溶液的弹性数之间相差1个数量级,而液滴尺寸随之变化的幅度远小于弹性数的变化幅度,与两相流率比和连续相毛细数对液滴尺寸的影响相比PEO水溶液的弹性对弹状液滴尺寸影响很小,可以忽略不计。 目前,文献中关于液滴的形成机理主要有剪切机理和挤压机理。Thorsen等[21]首先提出了剪切机理,认为黏性力在液滴生成过程中占主导作用,液滴的大小受到连续相毛细数影响。Garstecki等[22]提出的挤压机理认为连续相的挤压力主导液滴的生成,液滴尺寸与油水两相流率比紧密相关,与微通道宽度相比较长的液滴的生成主要由挤压机理主导,而较小的液滴的生成则由剪切机理控制。 基于以上两种机理,Cubaud等[5]研究了分散相流体为高黏情况下的液滴尺寸,以l/wc=2.5为分界点,在两个液滴长度范围内分别提出了十字聚焦微通道中的液滴尺寸关联式 Fu等[6]以l/wc=2.35为分界点,同样在两个范围内提出了液滴尺寸的预测式 将Cubaud等[5]和Fu等[6]提出的液滴尺寸关联式与实验结果进行比较,平均相对误差分别为36.66%、29.22%,最大相对误差分别为89.11%、53.71%,其中相对误差的表达式为 平均相对误差的表达式为 由于Cubaud等[5]和Fu等[6]实验所用的物系均为牛顿流体,提出的液滴尺寸关联式与实验结果之间的偏差较大,而PEO水溶液具有黏弹性和剪切变稀性,因此文献中建立的模型无法准确预测液滴尺寸,需要进行修正。 Fu等[11]研究了十字聚焦微通道内气泡在黏弹性流体中的生成过程,分析说明了气泡的生成受到界面张力、黏性力、惯性力和分散相压力的共同作用,并以气液两相流率比和连续相毛细数及Reynolds数Re建立了气泡尺寸的预测模型。对于相同的两相流率比,液滴尺寸的大小取决于两相的绝对流率,因此需要在液滴尺寸预测式中同时考虑两相流率的绝对大小和相对比值的影响。引入连续相的Reynolds数,可将连续相体积流率的绝对大小体现在模型中,再结合两相流率比即可得到同时考虑两相流率的绝对大小和相对比值影响的关联模型。 本研究采用油水两相流率比和连续相毛细数及Reynolds数关联弹状液滴的尺寸,在两个液滴长度范围内得到弹状液滴尺寸的预测式分别为 图8比较了由式(13)得到的弹状液滴尺寸计算值与实验值,在两个液滴长度范围内的平均相对误差分别为5.05%和2.85%,最大相对误差分别为16.37%和18.66%。结果表明预测模型可以很好地用于微通道内黏弹性流体中弹状液滴生成尺寸的预测。 图8 弹状液滴长度的计算值与实验值比较Fig.8 Comparison between calculated values and experimental data of slug droplet sizes 利用高速摄像仪对十字聚焦微通道内硅油液滴在黏弹性流体PEO水溶液中的生成过程进行了研究。观察到了弹状流、滴状流和喷射流3种流型,以连续相毛细数和分散相Weber数考察了流型及流型转变。研究了弹状液滴生成过程的颈部动力学,在快速夹断阶段分散相的颈部宽度与剩余时间之间满足幂律规律Wm∝(T−t)1/3。考察了两相流率、连续相毛细数及弹性数对弹状液滴尺寸的影响。结果表明:弹状液滴尺寸随连续相流率、毛细数及弹性数增加而减小,随分散相流率增加而增加,连续相弹性对液滴尺寸的影响相对较小。根据液滴生成的剪切机理和挤压机理,以油水两相流率比和连续相毛细数及Reynolds数为变量参数提出了弹状液滴尺寸的预测关联式,预测值与实验值吻合良好。 符号说明 Ca ——毛细数,Ca=ηu/σ c*——临界交叠浓度,% El ——弹性数,El=λeffηc,0/ρcw2c l ——液滴长度,m MW——聚合物重均分子量 n ——流动指数 Qc,Qd——分别为连续相体积流率、分散相体积流率,ml·h−1 Re ——Reynolds数,Re=wcuρ/η We ——Weber数,We=ρwu2/σ Wm——分散相颈部宽度,m wc——微通道宽度,m δ ——相对误差 δ−——平均相对误差 η ——黏度,Pa·s θ ——接触角,(°) λ ——时间常数,s λeff——松弛时间,s ρ ——密度,kg·m−3 σ ——界面张力,N·m−1 References [1] 陈光文, 袁权. 微化工技术 [J]. 化工学报, 2003, 54(4): 427-439. DOI: 10.3321/j.issn: 0438-1157.2003.04.004. CHEN G W, YUAN Q. Micro chemical technology [J]. Journal of Chemical Industry and Engineering(China), 2003, 54(4): 427-439. DOI: 10.3321/j.issn: 0438-1157.2003.04.004. [2] ZHAO C X, MIDDELBERG A P J. Two-phase microfluidic flows [J]. Chemical Engineering Science, 2011, 66(7): 1394-1411. [3] DREYFUS R, TABELING P, WILLAIME H. Ordered and disordered patterns in two-phase flows in microchannels [J]. Physical Review Letters, 2003, 90(14): 144505. [4] FU T T, MA Y G, LI H Z. Hydrodynamic feedback on bubble breakup at a T-junction within an asymmetric loop [J]. AIChE Journal, 2014, 60(5): 1920-1929. [5] CUBAUD T, MASON T G. Capillary threads and viscous droplets in square microchannels [J]. Physics of Fluids, 2008, 20(5): 053302. [6] FU T T, WU Y N, MA Y G, et al. Droplet formation and breakup dynamics in microfluidic flow-focusing devices: from dripping to jetting [J]. Chemical Engineering Science, 2012, 84: 207-217. [7] LIU H, ZHANG Y. Droplet formation in microfluidic cross-junctions [J]. Physics of Fluids, 2011, 23(8): 082101. [8] UTADA A S, LORENCEAU E, LINK D R, et al. Monodisperse double emulsions generated from a microcapillary device [J]. Science, 2005, 308(5721): 537-541. [9] ZHAO C X. Multiphase flow microfluidics for the production of single or multiple emulsions for drug delivery [J]. Advanced Drug Delivery Reviews, 2013, 65(11/12): 1420-1446. [10] HUEBNER A, SHARMA S, SRISA-ART M, et al. Microdroplets: a sea of applications? [J]. Lab on a Chip, 2008, 8(8): 1244-1254. [11] FU T T, MA Y G, FUNFSCHILLING D, et al. Breakup dynamics of slender bubbles in non-Newtonian fluids in microfluidic flowfocusing devices [J]. AIChE Journal, 2012, 58(11): 3560-3567. [12] STEINHAUS B, SHEN A Q, SURESHKUMAR R. Dynamics of viscoelastic fluid filaments in microfluidic devices [J]. Physics of Fluids, 2007, 19(7): 073103. [13] LEE W, WALKER L M, ANNA S L. Competition between viscoelasticity and surfactant dynamics in flow focusing microfluidics [J]. Macromolecular Materials and Engineering, 2011, 296(3/4): 203-213. [14] BYRON B R, CARREAU P J. A nonlinear viscoelastic model for polymer solutions and melts—Ⅰ [J]. Chemical Engineering Science, 1968, 23(5): 427-434. [15] DEL GIUDICE F, D’AVINO G, GRECO F, et al. Effect of fluid rheology on particle migration in a square-shaped microchannel [J]. Microfluidics and Nanofluidics, 2015, 19(1): 95-104. [16] REN Y, LIU Z, SHUM H C. Breakup dynamics and dripping-to-jetting transition in a Newtonian/shear-thinning multiphase microsystem [J]. Lab on a Chip, 2015, 15(1): 121-134. [17] FU T T, FUNFSCHILLING D, MA Y G, et al. Scaling the formation of slug bubbles in microfluidic flow-focusing devices [J]. Microfluidics and Nanofluidics, 2010, 8(4): 467-475. [18] FU T T, MA Y G, FUNFSCHILLING D, et al. Bubble formation and breakup mechanism in a microfluidic flow-focusing device [J]. Chemical Engineering Science, 2009, 64(10): 2392-2400. [19] DOLLET B, VAN HOEVE W, RAVEN J-P, et al. Role of the channel geometry on the bubble pinch-off in flow-focusing devices [J]. Physical Review Letters, 2008, 100(3): 034504. [20] TIRTAATMADJA V, MCKINLEY G H, COOPER-WHITE J J. Drop formation and breakup of low viscosity elastic fluids: effects of molecular weight and concentration [J]. Physics of Fluids, 2006, 18(4): 043101. [21] THORSEN T, ROBERTS R W, ARNOLD F H, et al. Dynamic pattern formation in a vesicle-generating microfluidic device [J]. Physical Review Letters, 2001, 86(18): 4163-4166. [22] GARSTECKI P, FUERSTMAN M J, STONE H A, et al. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up [J]. Lab on a Chip, 2006, 6(3): 437-446. DOI:10.11949/j.issn.0438-1157.20151056 中图分类号:TQ 021.4 文献标志码:A 文章编号:0438—1157(2016)02—0504—08 基金项目:国家自然科学基金项目(21276175, 21106093, 91434204);天津市自然科学基金项目(13JCQNJC05500)。 Corresponding author:Prof. MA Youguang, ygma@tju.edu.cn supported by the National Natural Science Foundation of China (21276175, 21106093, 91434204) and the Natural Science Foundation of Tianjin(13JCQNJC05500). Formation and size prediction of slug droplet in viscoelastic fluid in flow-focusing microchannel ZHANG Qindan, FU Taotao, ZHU Chunying, MA Youguang Abstract:A high-speed camera was utilized to observe the formation of the droplet in viscoelastic fluid in flow-focusing microchannel. The microchannel with a square section of 600 μm×600 μm was used in the experiment. Silicone oil and polyethylene oxide (PEO) solution (0.1%,0.3%,0.6%) with 0.3% surfactant sodium dodecyl sulfate (SDS) were used as dispersed and continuous phases, respectively. Three flow patterns were observed: slug flow, dripping flow and jetting flow. The transition lines for different flow patterns were obtained. The dynamics of breakup for slug droplets was studied. The effects of two-phase flow rates, capillary number and elasticity number of the continuous phase on the size of slug droplet were investigated experimentally. The results indicated that the size of slug droplet decreased with increasing flow rate, capillary number and elasticity number of the continuous phase, but it increased with increasing flow rate of the dispersed phase. The impact of the elasticity of the continuous phase on slug droplet size was relatively small. The correlations for predicting the size of slug droplet were proposed by taking the ratio of two-phase flow rates, and the capillary number and Reynolds number of the continuous phase into account. The prediction result agreed well with the experimental data. Key words:microchannels; two-phase flow; hydrodynamics; droplet; viscoelasticity; size prediction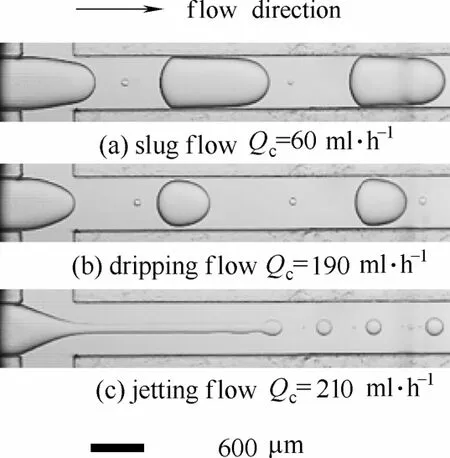


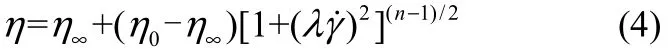

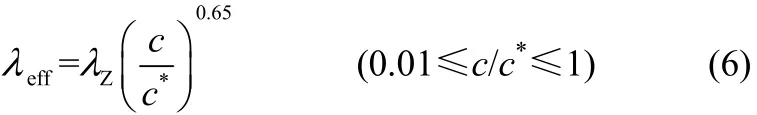

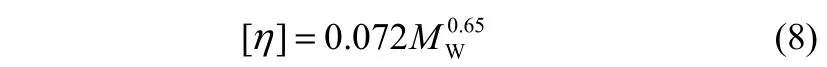
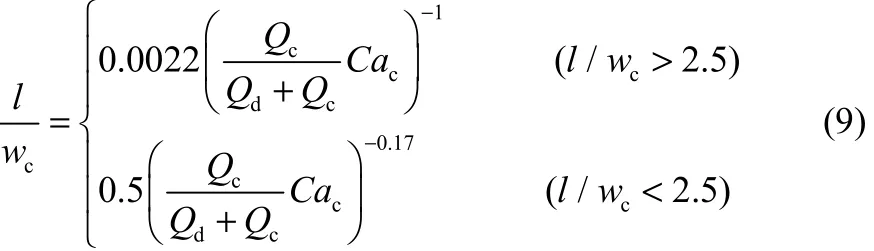

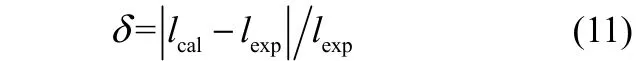
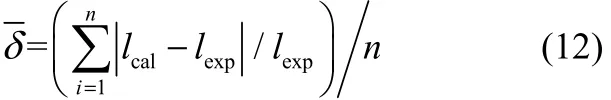
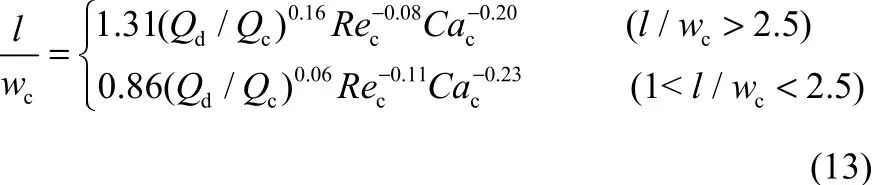
3 结 论
(School of Chemical Engineering and Technology, State Key Laboratory of Chemical Engineering, Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), Tianjin University, Tianjin 300072, China)

