水盐体系相平衡研究进展
张杰,史学伟,赵双良,宋兴福,于建国(华东理工大学化学工程国家重点实验室,上海 0037;华东理工大学国家盐湖资源综合利用工程技术研究中心,上海 0037)
水盐体系相平衡研究进展
张杰1,2,史学伟1,赵双良1,宋兴福1,2,于建国1,2
(1华东理工大学化学工程国家重点实验室,上海 200237;2华东理工大学国家盐湖资源综合利用工程技术研究中心,上海 200237)
摘要:水盐体系相平衡与相图是无机盐化工的理论基础,对水盐体系相平衡的研究可为盐湖盐类资源的综合开发利用提供理论支持。从水盐体系相平衡实验和理论研究两个方面,综述了近期国内外相关研究进展及研究方法。重点介绍了稳定相平衡和介稳相平衡体系相图测定方法及特点,概述了相区间和结晶类型变化的影响因素;从热力学模型法、统计力学理论和分子模拟3个方面介绍了水盐体系相平衡的理论研究思路及基于液-固化学势平衡的研究现状,并讨论了3类方法在相平衡研究上的可能发展方向。最后总结了该领域的一些研究热点,并对水盐体系相平衡的研究趋势作了展望。
关键词:水盐体系;相平衡;相图;盐湖资源
2015-07-22收到初稿,2016-01-15收到修改稿。
联系人:赵双良,宋兴福。第一作者:张杰(1991—),男,硕士研究生。
Received date: 2015-07-22.
引 言
盐湖资源是重要的无机盐矿产资源,其中沉积的盐类矿物多达200种。目前,人类已经从盐湖中大量开采石盐、碱、芒硝以及钾、锂、镁、硼、溴、硝石、石膏和医用淤泥等基本化工、农业、轻工、冶金、建筑和医疗等重要原料。盐湖中还富存着具有工业开采价值的铷、铯、钨、锶、铀以及氯化钙、菱镁矿、沸石、锂蒙脱石等资源[1]。世界上几个典型盐湖的主要化学组成列于表1。
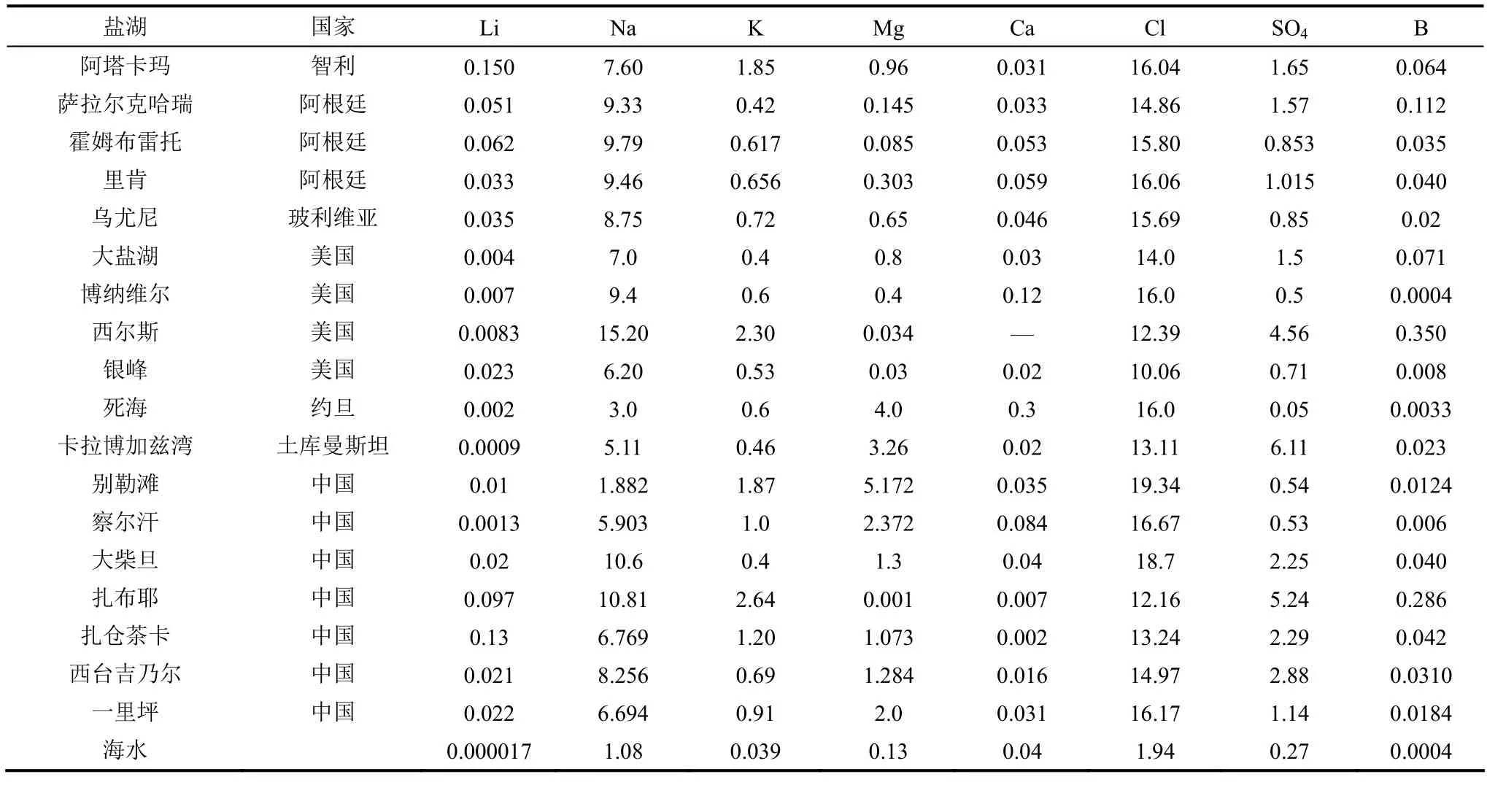
表1 世界主要盐湖及海水的化学组成(以质量分数计)[2]Table 1 Chemical composition of various salt lake brines around world (in mass percent)[2]
我国是世界上为数不多现代盐湖发育良好的国家之一,盐湖数量多、类型全、资源丰富、富含稀有元素。其中大小盐湖总共1000多个,面积大于1 km2的盐湖就有731个,总面积近2.8×104km2,主要分布在青海、新疆、西藏和内蒙古等省区[3]。钾、锂、硼、镁和钠的液、固盐类矿产储量十分巨大, 其中石盐总储量超过900亿吨,镁盐超过30亿吨[4]。我国近期开采盐类资源如石盐约350万吨、硫酸钠约200万吨、钾盐(折算KCl)300万~350万吨、硼酸盐(折算为硼砂)8万~10万吨、硫酸镁3万吨、水氯镁石5万~8万吨[4]。虽开采量较大,但开采出的盐类资源只占我国盐湖盐类资源总储量中极少的一部分,盐湖资源开发利用空间巨大。
盐湖资源开采主要采用相分离和萃取的方法,金属盐提取工艺的开发离不开水盐体系相图。水盐体系相图是水盐体系在一定相平衡条件下(如恒定温度、压强等)各组元在不同配比情况下的溶解度曲线,它是确立无机盐相分离条件以及开发卤水资源分级回收工艺的依据。因此,水盐体系相平衡的研究具有十分重要的意义,它是综合利用各类盐湖盐类资源的理论基础。
国内外学者针对水盐体系相平衡开展了大量实验和理论研究工作:发展了水盐体系相图测定方法,测定和完善了一系列水盐体系在不同温度下的溶解曲线;从离子间的相互作用机制出发建立了一系列相平衡计算模型,并能较为准确地预测水盐体系的相图。本文概述了水盐体系相平衡实验和理论两方面的研究方法和进展,讨论了该领域的研究热点,并对水盐体系相平衡研究的发展方向作了展望。
1 水盐体系相平衡实验研究进展
近年来,国内外学者对水盐体系稳定相平衡数据的测定进行了大量的工作,研究体系主要集中在Li+, Na+, K+, Rb+, Cs+, Mg2+, Ca2+//Cl−, Br−, NO−3,, borate-H2O体系的三元、四元和五元子体系,研究温度集中在288~348 K,并基于相平衡数据分析其中的结晶固相类型及其结晶区大小,此外也会涉及平衡液相的物性测定等工作[5],下面从研究类型、研究方法和研究体系3个方面介绍国内外水盐体系相平衡实验研究进展。
1.1实验研究类型
水盐体系相平衡实验研究可分为两大类:稳定相平衡和介稳相平衡。稳定相平衡研究主要测定体系处于热力学平衡状态时的相平衡数据,不考虑实际环境中水分蒸发等因素的影响。而盐湖实际析盐过程都是在一定风速、日照、蒸发速率等环境条件下进行的,考虑到结晶动力学因素的影响,系统实际处于介稳相平衡状态。此时稳定相平衡数据无法反映体系实际的相平衡状态,因此需进一步开展介稳相平衡的研究。鉴于平衡条件的不同,同一水盐体系的介稳相图与稳定相平衡条件下的相图有较大的差异。图1是四元体系Li2SO4-K2SO4-MgSO4-H2O 在298.15 K稳定相平衡[6]和288.15 K介稳条件[7]下的相图。两个体系温度相近,介稳条件对于固相结晶区有较大的影响。
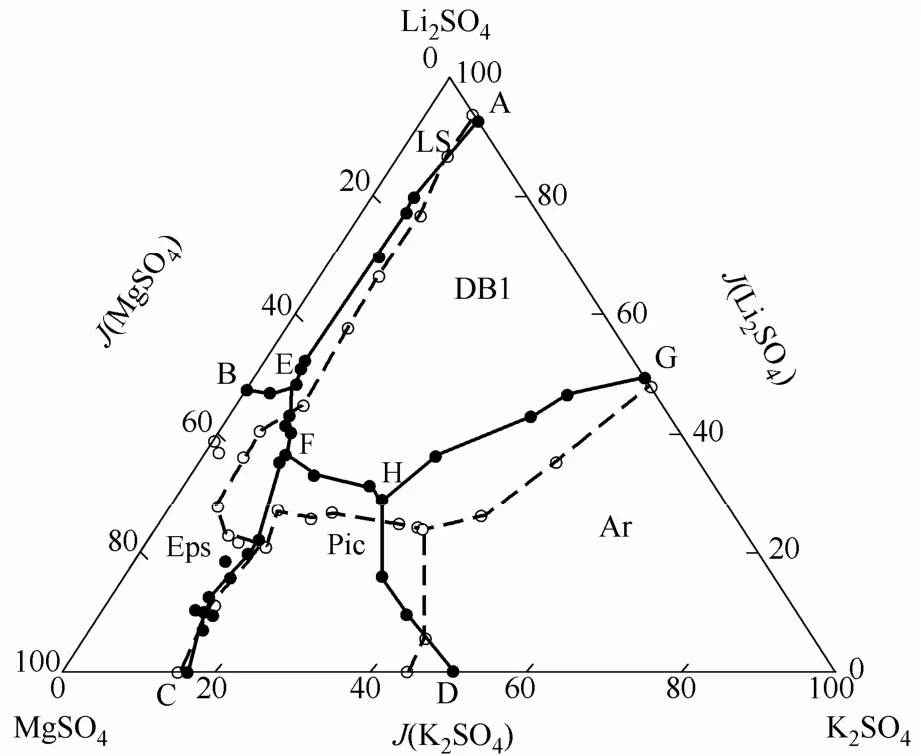
图1 四元体系Li2SO4-K2SO4-MgSO4-H2O稳定和介稳相图Fig.1 Stable and metastable phase diagrams of quaternary salt-water system Li2SO4-K2SO4-MgSO4-H2O(metastable conditions with evaporation rate of 4—6 kg·m−2·d−1, relative humidity of 20%—30%, air flowing velocity of 3.5—4.0 m·s−1)○ −298.15 K stable phase equilibrium data;● −288.15 K metastable phase equilibrium data
稳定相平衡研究主要针对热力学平衡态,为理论研究提供基础数据同时,也给工艺路线的选择提供基本依据。而介稳相平衡研究根据具体的实际情况来确定系统模型参数,对生产工艺的开发指导作用更具针对性。稳定相平衡研究起步较早[5-6, 8-13],研究得较为充分;介稳相平衡研究近年来受到越来越多的关注[7, 14-16]。总的来说,介稳相平衡研究尚局限于某水盐体系在特定介稳条件下相平衡数据的测定,且介稳条件一般依据盐湖自然条件如日照、风速、空气相对湿度等环境条件确定,而系统性的研究不同介稳条件对于同一类体系相图的影响还不多见。系统的研究介稳条件的影响,不仅为非平衡态热力学理论的发展提供数据,还将为调控结晶条件提高金属盐的提取效率提供思路。
1.2实验研究方法
稳定相平衡数据的测定通常采用等温溶解平衡法[5-6, 8-13],而水盐体系介稳相平衡研究普遍采用等温蒸发法[7, 14-16],除此之外也有学者提出一些新的方法及考察条件,下面将分别介绍。
1.2.1稳定相平衡测定水盐体系稳定相平衡的测定主要采用等温溶解平衡法,即通过配制不同初始组成的混合盐和适量的水(保证固体盐过量)一起密闭于恒温容器中,达到溶解平衡后通过测定液相组成并分析固相晶形,确定该体系的相平衡数据,进而绘制相应的相图。取样分析过程中,取上层清液进行化学分析或者仪器分析(一般采用ICP-OES)进行组成测定,并根据需要测定其他相关物性;固相通过抽滤、洗涤,在研究温度下干燥后在偏光显微镜下观察其晶型,并进一步利用湿渣法[17-18]或XRD确定平衡固相的物质组成。
除此之外,也有学者提出了一些其他的测定方法。Kwok等[19]在测定Li+, Mg2+//Cl−, SO42−-H2O在298 K下的稳定相图时,采用了等温固相消失法,并印证了该方法与等温溶解平衡法在实验数据测定上的一致性。与后者相比,等温固相消失法的配样过程有所不同,先配制混合干盐初始组成并部分溶解于恒温容器中,之后不断加入已知量的水至固相恰好完全溶解。Atbir等[20-21]发展了综合法(synthetic method)进行水盐体系稳定相平衡测定。该法与固相消失法相似,区别在于综合法依据体系发生相变时电导率会出现突变的原理来判定固体是否溶解完全。综合法对于用肉眼观测难以准确判定平衡终点的体系提供了一种十分有效的相平衡测定方法。
这些方法各有优缺点。常规的等温溶解平衡法可以通过各种分析手段确定各组成平衡固相的物质组成,在确定共饱和点方面有明显优势。其难点主
要来自于对溶解度干扰因素的避免以及对溶液中盐浓度的精确测定。等温固相消失法的优点在于初始组成的称量数据较为可靠,同时不会引入取样和各离子滴定分析过程中的误差,因此测定结果较为准确,特别是对于相图中个别相区较窄的水盐体系,采用此法可以较为精确地得到饱和组成。但是该方法只能测定相图中指定组成的饱和溶解度,并不能确定该组成平衡固相的物质组成,因此不太适合确定相图中的共饱和点。针对实际研究问题,可以根据需要选择合适的研究方法。如等温固相消失法可以结合湿渣法确定共饱和点组成。Yin等[22]在研究KNO3-LiNO3-NaNO3-H2O四元体系稳定相平衡时,体系中Li+和Na+同时存在,采用等温溶解平衡法难以精确测定溶液中两种离子的组成。他们采用等温固相消失法确定了KNO3-LiNO3-NaNO3-H2O四元体系在298.1 K和308.5 K,以及LiNO3-NaNO3- H2O三元自体系在323.1 K下的稳定相图。
1.2.2介稳相平衡测定方法采用等温蒸发法进行介稳相平衡测定过程中,所选择的实验条件通常为模拟体系对应盐湖所在地区的气候环境条件。而对于其他介稳条件的考察,也有学者做过相关工作,Zhou等[15]采用等温蒸发结晶的方法考察了四元体系Na+, Mg2+//Cl−, SO42−-H2O在373.15 K下、蒸发强度控制在108~144 kg·m−3·h−1时沸腾蒸发过程中的介稳相关系,通过逐个考察各结晶固相的介稳区,并对比该体系373.15 K下的稳定相平衡的文献数据,发现各结晶区变化较大。
需注意的是,同一体系介稳相图与稳定相图之间的差异会随着介稳条件的改变发生不同程度的变化,因此工业上可利用这一特点,通过改变介稳条件来达到工业上某些特殊的提取要求。不过对于介稳相平衡研究通常只考察某一特定的介稳条件,对于同一体系不同介稳条件下的相平衡研究工作相对较少。
1.3实验研究体系
相平衡研究中受到关注的水盐体系主要集中在Li+, Na+, K+, Rb+, Cs+, Mg2+, Ca2+//Cl−, Br−, NO3−,, borate-H2O体系的三元、四元和五元子体系。对于不同体系,其结晶固相组成及结晶区大小存在较大差异。此外,一些特殊的体系会有复盐或固溶体等特殊形式的结晶固相生成,如对于五元体系在298 K下会有复盐白钠镁矾[Na2Mg(SO4)2·4H2O]生成[23]。此外,对于同时含有K+、Rb+/Cs+和Cl−的体系[11, 14]以及K+/Na+、Cl−和Br−的体系[12-13]通常分别会有固溶体(K, Rb)Cl或(K, Cs)Cl以及Na(Cl, Br)或K(Cl, Br)生成。除了常规水盐体系的相平衡研究,国内外学者还考察了添加溶质或溶剂对水盐体系相平衡的影响。Zeng等[24]测定了四元体系MgCl2-LiCl-NH4Cl-H2O在298.15 K下的溶解度数据,并利用Pitzer-Simoson-Clegg(PSC)模型进行了理论研究,讨论了氨气在盐湖除镁工艺中的应用。Hu等[25-26]对稀有碱金属铷、铯盐-混合溶剂体系相化学开展了一系列的研究工作,为稀碱金属水盐体系萃取工艺的开发提供了大量的基础数据。Taboada等[27]通过测定298.15 K下NaCl+KCl+Mg(OH)2在不同浓度氨-水溶剂中的溶解度,提出了利用氨气分离上述体系中的单盐的可行方案,即在分离NaCl和KCl之前先通入氨气使Mg(OH)2完全沉淀,而后进行NaCl和KCl的分步结晶。Witkamp等[28]测定了323~363 K 下Na2CO3+NaHCO3在不同组成的乙二醇-水混合溶剂中的溶解度,发现该体系的结晶固相中没有溶剂化物出现。随着乙二醇浓度的增加,的溶解度逐渐减小,而的溶解度则是先减小后增加,同时,含结晶水的结晶固相(如Na2CO3·NaHCO3·2H2O)的稳定区也随之减小(即转变温度升高),而无结晶水的结晶固相(如Na2CO3·3NaHCO3)的稳定区则逐渐增大(即转变温度降低),据此,可以通过控制乙二醇的浓度来调控晶体的组成。利用添加剂调控相图结晶区域为水盐体系无机盐的分离和提纯提供了新的工艺开发思路。
水盐体系不同研究类型涉及的相平衡实验研究方法、研究体系和应用领域简单归纳在表2中。

表2 水盐体系相平衡实验研究Table 2 Experimental study on phase equilibria of salt-water systems
2 水盐体系相平衡理论研究进展
水盐体系相平衡的理论研究方法可分为三大类:热力学模型法、统计力学理论和分子模拟。其中,热力学模型法发展较早,计算相对简单,应用也更为广泛。水盐体系的相平衡本质上是溶解平衡和电离平衡,即平衡条件下电离的盐在溶液中的化学势与其在对应的固相中的化学势相等。因此水盐体系相平衡研究本质上是计算系统组元的化学势或活度系数。
2.1水盐体系的热力学模型
水盐体系热力学模型中,最有名的是Pitzer模型及其改进模型。1973年Pitzer[29]根据德拜-休克尔理论(Debye-Huckel equation)提出了强电解质离子交互模型,这是一种半经验式的统计力学电解质溶液理论,它将德拜-休克尔理论拓展到了更高浓度(5~6 mol·L−1)的电解质溶液。Pitzer模型包含过量焓的3种贡献:①离子间的长程相互作用;②短程硬球效应位能,其主要部分是两离子之间的排斥能;③三离子间的排斥能,它是很小的项,只有在离子浓度极高时贡献才明显。Pitzer模型的一个重要特征就是所有参数都可通过单一电解质和含相同离子的二盐溶液的测定来估算,对于更复杂的混合物,不需要引入新的参数,即利用Pizter模型中的耦合参数和由单一盐溶液溶解度的实验值,Pitzer模型能用于预测混合盐体系中固体溶解度。对于离子强度较小的情况,Pitzer模型可以很好地预测大部分水盐体系的活度系数,但离子强度较大时,Pizter模型与实验的偏差较为明显,且随着离子强度的增大而增大。
Pitzer模型提出之后,有许多学者在其基础上进行了创造性的整理和改进。如Pitzer和李以圭[30-31]提出了以摩尔分数为浓度单位的、新的过量Gibbs自由能表达式,得到了Pitzer-Li方程,此方程已成功用于高达823 K及108Pa时,从无限稀释到饱和溶解度的NaCl-H2O体系的热力学函数计算。1992年Clegg和Pitzer[32]在Pitzer-Li方程与Pitzer-Simonson方程的基础上改进,提出了Clegg-Pitzer方程,适用于高浓度混合电解质水溶液和混合溶剂体系。不过Clegg-Pitzer方程在实际计算时非常复杂,为此Li和Mather[33-34]对其进行了简化,只考虑两粒子及三中性粒子作用项,略去了含离子的三粒子作用项和各种四粒子作用项,得到了Li-Mather方程,该方程可用于高浓度及混合溶剂体系,并成功应用于带有电离平衡的酸性气体(CO2、H2S)在各种醇-胺-水混合溶剂体系中的溶解度计算。
除此之外,从半经验的溶液模型出发,许多其他模型和理论也得到了很好的发展和应用。在这些理论中,离子的化学势一般包含两部分贡献:长程静电作用贡献和短程相互作用贡献。前者主要通过Poisson方程计算,而短程相互作用贡献的计算模型比较多,根据溶剂的处理方法不同又可大致分为两类:一类把溶剂当作连续介质,此时离子的短程作用仅考虑硬球排斥,其化学势贡献通常可通过Carnahan Starling硬球状态方程[35]计算;另一类则将溶剂也与离子一样当作作用粒子处理,此时离子、分子短程相互作用可用van der Waals相互作用描述,其化学势贡献可通过MBWR状态方程计算[36]。当溶剂为混合溶剂且溶剂组元变化时,采用非连续介质溶剂模型是必需的。Renon和Prausnitz[37]从局部浓度出发提出的NRTL属于此类。1982年,Chen 等[38]将Pitzer-Debye-Huckel理论与局部模型中的NRTL方程相结合,提出电解质NRTL(electrolyte NRTL)方程应用于电解质溶液的计算,并取得了成功。Li等[39-40]在这方面也做出了创造性贡献。近年来还发展了离子水化理论和离子缔合理论。其中Lu和Maurer[41]发展了离子单级水化模型可用于预测混合电解质水溶液的离子活度系数,无须引入混合参数;张锁江和韩世钧[42]发展了SRE离子水化模型。
热力学模型法能够用较少的参数来构建化学势(活度系数)函数,计算较为简单,应用非常方便。但其参数往往采用经验/半经验的方法获得,而且依赖于数据库的使用。对于数据库中不存在的盐类组成的水盐体系,该方法的可靠性难以得到保证。此外,模型法只能应用于热力学平衡条件下水盐体系的相平衡计算,对于介稳体系的相平衡研究必须发展非平衡态热力学,这是传统热力学的一个重要挑战。
2.2水盐体系的统计力学理论
水盐体系本质上是电解质溶液,对于电解质溶液的研究,统计力学发展了许多成功的理论,包括泊松-玻耳兹曼方程(Poisson-Boltzmann equation)、微扰理论(perturbation theory)、积分方程理论(integral equation theory)和密度泛函理论(density functional theory)等。这些统计力学理论从粒子的相互作用出发,考虑了粒子之间的长程和短程相互作用,通过统计力学框架构建体系的热力学函数,从而能够较好预测系统组元的化学势。其中积分方程理论和密度泛函理论是两个极具代表性的现代流体统计力学理论[43],近几十年得到了迅速发展,已广泛应用于多个学科中流体系统的热力学性质和微观结构研究。
积分方程理论以电解质溶液的总关联函数和直接关联函数之间的积分关系为核心,求解这个方程即可获得描述溶液结构的各粒子的径向分布函数,从而预测离子的化学势。积分方程的求解需要联立另外一个封闭关系(closure)。常见的封闭关系有超网链近似(hypernetted-chain approximation)、Percus-Yevick近似以及平均球近似(mean spherical approximation)等。根据所研究模型系统的复杂程度,可用简单积分方程或分子积分方程理论来研究。前者针对球形分子系统,后者研究多原子分子组成的体系。分子积分方程理论又发展出了RISM理论和MOZ理论,前者以位点-位点(site-site)的关联函数为研究目标,而后者以分子与分子之间的关联函数为研究对象。由于求解方便,RISM理论应用较为广泛,目前已出现相关商业软件计算流体系统的结构与热力学性质。
经典密度泛函理论是积分方程理论的姊妹理论,它把系统的微观结构与宏观热力学函数通过密度泛函连接起来,即巨势可以表示为密度分布函数的泛函,在平衡态条件下,通过对巨势求泛函变分即可获得系统平衡态结构和对应的热力学性质[44-46]。经过几十年的发展,经典密度泛函已经从定性计算方法发展为定量计算工具,可准确、快速地预测溶质的溶剂化自由能[47-48]。应用经典密度泛函理论研究水盐体系相图有两种发展方向:第一是结合Percus方法把水盐体系当作非均相系统处理,计算盐组元的化学势以及在晶体中的化学势[47];第二是把水盐体系当作均相系统处理,此时密度分布函数为常数,盐组元在溶剂中的化学势可通过自由能对密度求泛函计算[49-50]。
这些现代流体统计理论在水盐体系相平衡研究上应用尚少,但潜力巨大。基于分子尺度的流体统计理论不依赖经验参数,因而能够较为准确地预测不同体系的化学势。但统计力学理论系统性强,较难掌握,因而阻碍了它的广泛应用。另外,平衡态统计力学理论已经拓展到了非平衡态,涌现了如含时密度泛函理论等动力学理论,这些非平衡态统计力学理论的出现,为介稳体系相平衡研究提供了新的方法和思路。
2.3水盐体系的分子模拟研究
分子模拟是一种重要的理论研究手段。给定描述分子间相互作用的力学力场,分子模拟原则上能够准确预测系统的所有热力学和结构性质。溶解平衡时,溶质在固相中的化学势应当与其在液相中的化学势相等,根据这一热力学原理可以确定金属盐的溶解度。Cui和Harris[51]首次采用分子动力学模拟计算NaCl的溶解度,通过改变NaCl在溶液中的浓度,并计算对应的化学势,直到该化学势与固相NaCl盐中的化学势相等。根据同样的思想,Ferrario 等[52]发展了计算离子静电相互作用对化学势的贡献的方法,研究了氟化钾的溶解度。后来出现了其他各种改进的分子模拟方法。这些改进的方法在溶质化学势计算方面各有特色,但基本思路一致,都基于计算盐在溶解相和固相中的化学势,因此统称为化学势计算法[53]。
在化学势计算法中,固体盐组元(如NaCl)的化学势可以通过盐晶体的Gibbs自由能(Gs)对NaCl的分子数求导获得。而盐晶体的Gibbs自由能,可以通过对爱因斯坦固体的Gibbs自由能求微扰来计算,即Gs=GsEins+ΔAs+pΔVs,其中,GsEins是爱因斯坦固体的Gibbs自由能,可解析计算[54],ΔAs是从爱因斯坦固体到盐晶体的自由能变化,可以采用分子模拟通过热力学积分方法获得,ΔVs是在压强p条件下两个固体的平均体积之差。溶液中盐组元的化学势μv计算思路与上述方法类似,可采用微扰的方法通过分子模拟计算。

图2 用直接法计算NaCl溶解度的分子模拟模型[53]Fig.2 Modelling in direct method for evaluation of solubility of NaCl in water by using molecular simulation(left panel depicts crystalline NaCl solid and right panel for NaCl salt-water system)[53]
另一种通过分子模拟计算溶解度的方法是直接法(又叫作动力学法)。在直接法计算中,固体盐与溶液直接接触,构成一个界面系统(图2)。在溶解平衡条件下,获得该盐的饱和溶液,进而得到溶解度值[53]。在溶解-析出动力学模拟过程中,由于溶解比析出更为耗时,所以通常情况下,初始的界面系统由固体盐和过饱和水盐溶液构成,随着分子模拟的进行,盐溶液中的盐组元缓慢析出,最终达到溶解平衡。直接法计算盐组元的溶解度相对比较简单,模型也比较直观,但界面附近盐组元的密度分布急剧变化,为了确定均相水盐溶液中饱和盐浓度,往往需要建立较大的模型系统来排除界面效应,这极大增加了系统达到溶解平衡所需时间。直接法和化学势法研究盐的溶解度各有优缺点,两种方法给出的溶解度结果具有一致性。
分子模拟方法可用于研究水盐体系相图以及盐析效应等[55-57]。此外,介稳条件下水盐体系跟环境有粒子交换与能量交换,构建合适的交换模型,结合巨正则系综模拟和直接法(或化学势法),分子模拟法从原理上可拓展至介稳体系相平衡研究。
3 水盐体系相平衡研究热点
3.1温度效应
在盐湖资源开发过程中,往往需要知晓水盐体系在不同温度下的相图以及相图随温度变化的趋势。对比水盐体系在多个温度下的相图发现,随着温度的变化,相图中结晶区大小会发生变化,甚至会出现某个固相的结晶区消失或者新固相结晶区的出现等情况。对于不同的水盐体系,温度的影响也不尽相同。如Zeng等[14, 58-59]先后对四元体系LiCl-KCl-RbCl-H2O在298.15、323.15和348.15 K下的相图进行研究,该体系在这3个温度下的介稳相图见图3。从图中可以看到平衡固相并没有发生变化,而结晶区大小发生了变化,随着温度的升高固溶体(K, Rb)Cl的结晶区有所减小,与此同时KCl、RbCl和LiCl·H2O的结晶区有所增大;而Guo等[9]对三元体系Na2SO4-Li2SO4-H2O在288和308 K下稳定相平衡研究发现,该体系在308 K下的相图相比于288 K的而言,芒硝的结晶形式由Na2SO4·10H2O变成了Na2SO4,同时相图上又出现了一个新的结晶固相Li2SO4·Na2SO4,当然,其他各相区的大小也发生了变化。
在盐类资源开发过程中,盐湖昼夜温差较大。掌握不同体系的水盐相图随温度变化的规律,有利于精确掌控析盐组元和质量比,从而为盐湖开发工艺的优化提供支持。此外,可根据水盐体系在不同温度下析出组元,结合实际工业条件和生产需要,确定合理的蒸发和冷却结晶分离路线。
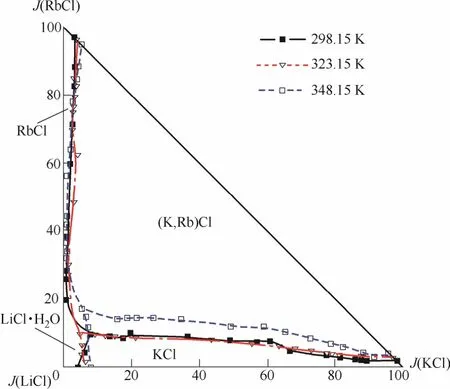
图3 四元体系LiCl-KCl-RbCl-H2O在298.15、323.15和348.15 K介稳相图[14, 58-59]Fig.3 Metastable phase diagram of quaternary salt-water system LiCl-KCl-RbCl-H2O at 298.15, 323.15 and 348.15 K[14, 58-59]
3.2盐效应
盐效应包括盐溶和盐析效应两种,其中绝大部分盐效应是盐析效应。盐析效应是指在溶液中,随一种盐组元的浓度增加另一种盐组元的饱和溶解度降低的现象。盐析效应普遍存在于水盐体系中,如图4所给的MgCl2-NaCl-H2O三元体系298 K相图中,由单变量曲线aE可以看出,随着氯化镁含量的增加,饱和溶液中氯化钠的量逐渐减小,直至饱和液相组成达到共饱和点,此时共饱和溶液中氯化钠的质量分数仅为0.3%。
盐析效应为析盐次序提供依据,是盐析结晶工艺设计和优化的基础。在生产过程中,可利用特定水盐体系的盐析效应,分离出所需工业原料。由华东理工大学国家盐湖资源综合利用工程技术研究中心开发并由青海盐湖海纳化工有限公司投产的钠法氢氧化镁制备技术[60],其中用到了氯化镁对氯化钠的盐析作用,在溶解六水氯化镁原料的同时结晶分离析出氯化钠晶体,并将其溶于淡盐水中送回电解车间,实现了电解盐水的循环利用。
3.3结晶固相类型
对于不同的水盐体系,析出的结晶固相类型不同,有单盐、水合盐、复盐和固溶体。其中单盐指的是一对最基本的阴阳离子组成的盐,如NaCl、NH4Cl、K2SO4等;水合盐指的是单盐分子结合了若干个水分子组成的盐。水合盐在不同温度下所结合的水分子数也不同,如对于CaCl2的结晶形式,298 K时为CaCl2·6H2O,308 K时为CaCl2·4H2O,323 K时为CaCl2·2H2O。复盐一般指的是两种或两种以上单盐组成的盐,而且对于大多数水盐体系中形成的复盐,有着特定的矿物名称,如光卤石(KCl·MgCl2·6H2O)、白钠镁矾[Na2Mg(SO4)2·4H2O]等。固溶体亦被称为混晶,一般指的是两种盐在固相中形成的互溶物,且这种固体晶型是完全均匀的,如(K, Rb)Cl、Na(Cl, Br)、(LiCl·H2O, NH4Cl)等。
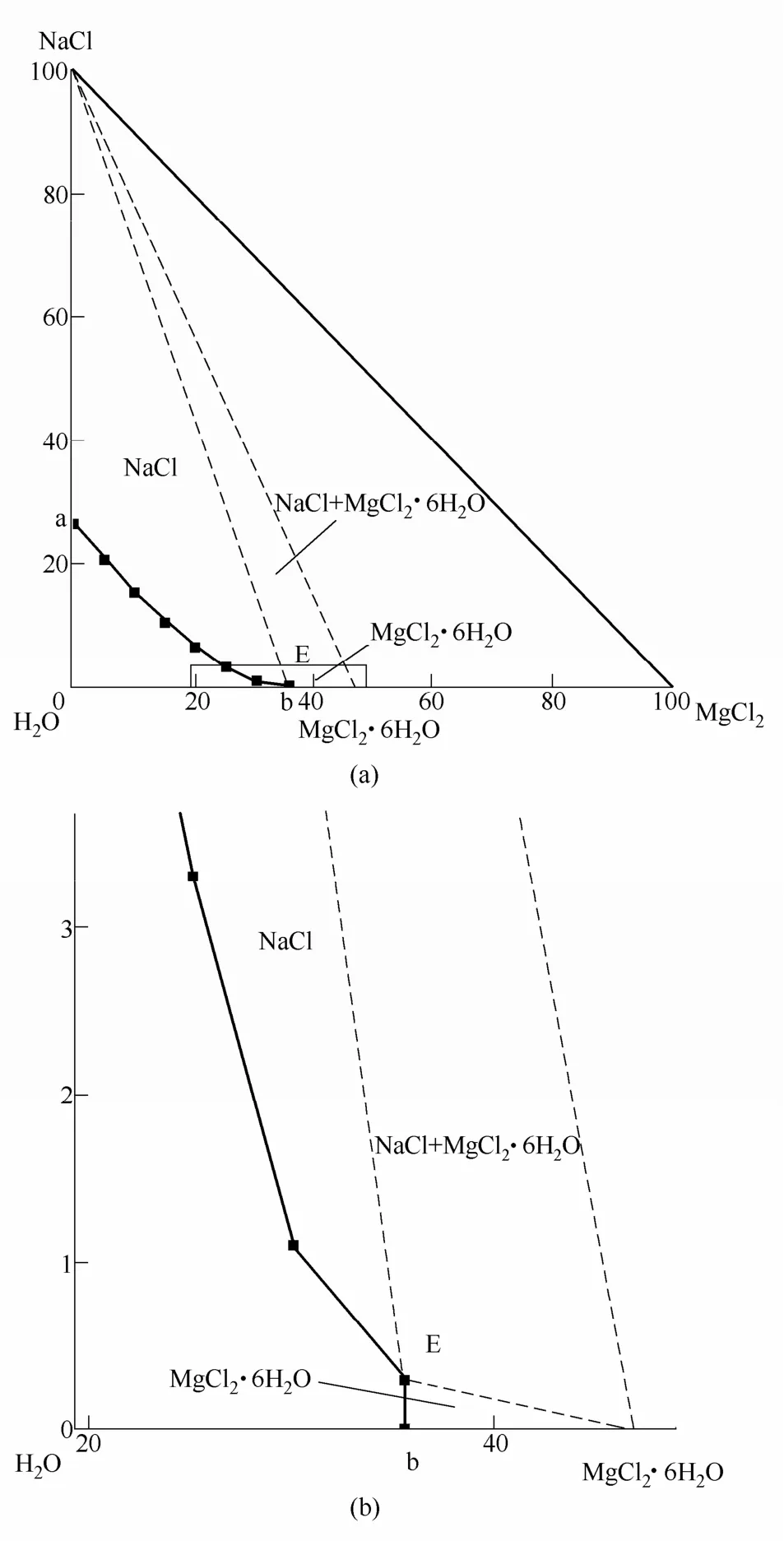
图4 MgCl2-NaCl-H2O三元体系298 K稳定相图(a)及其局部放大图(b)Fig.4 Stable phase diagram of ternary salt-water system MgCl2-NaCl-H2O at 298 K(a), and partial enlarged drawing(b)
在采用分子模拟和统计力学方法开展相图研究时,需预先知道结晶固相类型。如在分子模拟计算过程中,需计算固相中盐组元的化学势。结晶固相类型不同,则盐组元在固相中的化学势也会发生变化。另外,掌握结晶形成不同固相类型的机理,也是确定在不同条件下结晶类型的关键。这一方面的研究需定量计算不同晶体在溶液中生长的自由能变化,需结合量化计算和溶剂化自由能计算,这方面的进展尚不多见。
4 总结与展望
我国的盐湖资源非常丰富,然而目前资源开发十分有限,主要集中在钾、镁资源的开发利用上,如何更高效、更全面地开采盐湖资源是盐湖研究的一个重点。未来水盐体系相图基础研究工作应符合国家重大战略需求,将水盐体系相平衡研究跟盐湖盐类资源开发利用充分结合起来,使我国的盐类资源开发迈向一个更高的台阶。要实现这个目标,还需大力发展水盐体系相平衡基础研究,完善基础数据的测定和模块化建立。
总的来说,对于水盐体系相平衡的实验研究方法较为成熟,而且研究体系正不断丰富,水盐体系相平衡数据库的筹建正在有序展开。理论研究则相对滞后,大部分理论研究还基于热力学模型上,统计力学理论和分子模拟应用相对较少,而非平衡态统计力学的应用尚处于起步阶段。基于此,未来的水盐体系相平衡研究除了完善常见的几种水盐体系在遗漏温度下的溶解度数据以外,还可以从以下几个方面开展工作。
(1)进一步完善多元水盐体系相图的测定,为盐湖开发构建完整数据库。盐湖中除了常见的钾、钠、镁资源以外,还有许多碱金属如锂、铯、铷及其他稀有金属盐类资源,这一类盐类资源储量不多,但开发的价值较大。工业上对于这类浓度较低却含有高附加值的资源,通常先采用蒸发浓缩、吸附等方法浓缩富集,再通过反应结晶、萃取等手段进行分离提纯,如西藏扎布耶锂业高科技有限公司采用的“冷冻除碱硝-梯度太阳池升温沉锂”,中信国安科技发展有限公司采用的“煅烧法”提锂工艺[61],以及青海盐湖工业股份有限公司正在调试的离子筛吸附提锂技术。对于分离提纯阶段,则需要相关水盐体系相图数据作为理论依据,而对于这些盐类资源,相关相图数据较少,制约了这部分资源的开发利用。在未来的工作中,应结合实验和理论研究,开展横向(体系)和纵向(温度)相平衡研究,完善盐湖全面开发利用的基础数据库。
(2)深入探究各体系结晶固相形成机理及转变条件。对于部分水盐体系,其结晶固相中可能存在复盐和固溶体等非单盐结晶形式,而平衡固相的结晶形式也影响着相应相图的结晶区划分。目前,对于平衡固相的组成和类型则仅通过实验进行测定,而对其形成机理、同一物质的不同结晶固相类型的转变条件等方面缺少一个系统和深入的认知,从而一定程度上制约了水盐体系相平衡的理论研究和实际应用。因此,在未来工作中,可进一步加强关于结晶固相形成和转变方面的机理工作。
(3)相平衡研究由单一水盐体系向多相体系拓展。在盐湖资源开发过程中,对于结晶分离纯化工艺,采用添加特定溶剂的溶析结晶工艺较之蒸发结晶工艺,能耗更低[62-63],且溶析剂可以回收循环使用,同时,对于那些溶解度随温度变化较小的盐,采用溶析结晶工艺分离更具经济性。而确定溶析结晶工艺的关键是掌握溶析剂与原有水盐体系之间的相平衡关系,因此,对于无机盐在混合溶剂体系中的相平衡研究,是一个重要的相平衡领域研究方向,对盐湖资源的综合开发利用有着非常重要的意义。
(4)深入开展非稳态相平衡理论研究,构建动态溶解模型。目前,对于水盐体系的非稳态相平衡研究,其介稳条件主要选取特定盐湖的当地气候条件,研究目的主要集中在盐湖析盐规律的研究。盐湖析盐的实际过程中,受到温度、风力、空气相对湿度和水分蒸发速率等环境条件影响较大,此外,外源势场、受限空间以及盐水流动方式等对盐的溶解和析出行为也会产生较大影响。合理考虑这些外部因素,构建动态溶解模型,进一步发展非平衡态热力学和统计理论,是定量预测工业条件下的溶解度曲线、精确控制析盐过程的基础,对于非稳态工业结晶过程的精确调控有着十分重要的意义。
References
[1] 郑绵平, 卜令忠. 盐湖资源的合理开发与综合利用 [J]. 矿产保护与利用, 2009, (1): 17-22. ZHENG M P, BU L Z. Rational development and comprehensive utilization of salt lakes resources [J]. Conservation and Utilization of Mineral Resources, 2009, (1): 17-22.
[2] SONG P S, SUN B, ZENG D W. Solubility phenomena studies concerning brines in China [J]. Pure and Applied Chemistry, 2013, 85(11): 2097-2116.
[3] 马培华. 科学开发我国的盐湖资源 [J]. 化学进展, 2009, 21(11): 2349-2357. MA P H. Sustainable exploitation and comprehensive utilization of salt lake resources in China [J]. Progress in Chemistry, 2009, 21(11): 2349-2357.
[4] 郑绵平. 中国盐湖资源与生态环境 [J]. 地质学报, 2010, 84(11): 1613-1622. ZHENG M P. Salt lake resources and eco-environment in China [J]. Acta Geologica Sinica, 2010, 84(11): 1613-1622.
[5] ZENG Y, YANG H M, YIN H, et al. Study of the phase equilibrium and solution properties of the quinary systemB4O27−+H2O at T=298.15 K [J]. Journal of Chemical & Engineering Data, 2004, 49(6): 1648-1651.
[6] 房春晖, 李冰, 李军, 等. 四元体系Li+, K+,相关系和溶液物化性质的研究 [J]. 化学学报, 1994, 52(10): 954-959.
FANG C H, LI B, LI J, et al. Studies on the phase diagram and solution properties for the quarternary system Li+, K+,at 25℃ [J]. Acta Chimica Sinica, 1994, 52(10): 954-959.
[7] DENG T L, YU X, SUN B. Metastable phase equilibrium in the aqueous quaternary system (Li2SO4+K2SO4+MgSO4+H2O) at 288.15 K [J]. Journal of Chemical & Engineering Data, 2008, 53(11): 2496-2500.
[8] WOLLMANN G, VOIGT W. Solid-liquid phase equilibria in the system K2SO4-MgSO4-H2O at 318 K [J]. Fluid Phase Equilibria, 2010, 291(2): 151-153.
[9] GUO Y F, LIU Y H, WANG Q, et al. Phase equilibria and phase diagrams for the aqueous ternary system (Na2SO4+Li2SO4+H2O) at (288 and 308) K [J]. Journal of Chemical & Engineering Data, 2013, 58(10): 2763-2767.
[10] ZHOU H Y, ZENG D W, HAN H J, et al. Solubility isotherm of the system Li2SO4-K2SO4-MgSO4-H2O at 273.15 K [J]. Journal of Chemical & Engineering Data, 2013, 58(6): 1692-1696.
[11] HU B, SONG P, LI Y, et al. Solubility prediction in the ternary systems NaCl-RbCl-H2O, KCl-CsCl-H2O and KBr-CsBr-H2O at 25℃using the ion-interaction model [J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 2007, 31(4): 541-544.
[12] SANG S H, CUI R Z, HU J W, et al. Measurements of the solid-liquid equilibria in the quaternary system NaCl-NaBr-Na2SO4-H2O at 323 K [J]. Journal of Solution Chemistry, 2013, 42(8): 1633-1640.
[13] CUI R Z, SANG S H, HU Y X. Solid-liquid equilibria in the quaternary systems KCl-KBr-K2B4O7-H2O and KCl-KBr-K2SO4-H2O at 373 K [J]. Journal of Chemical & Engineering Data, 2013, 58(2): 477-481.
[14] YU X D, ZENG Y, YANG J Y. Solid-liquid isothermal evaporation metastable phase equilibria in the aqueous quaternary system LiCl+KCl+RbCl+H2O at 298.15 K [J]. Journal of Chemical & Engineering Data, 2012, 57(1): 127-132.
[15] ZHOU H, ZHANG J B, ZHANG H L, et al. Salt-forming regions of Na+, Mg2+//Cl−,system at 373.15 K in the nonequilibrium state of isothermal boiling evaporation [J]. Journal of Chemical & Engineering Data, 2012, 57(4): 1192-1202.
[16] SANG S H, ZHANG Z L, LI M. Solid-liquid metastable equilibria in quaternary system Li2SO4+Li2CO3+Li2B4O7+H2O at 288 K [J]. Chem. Res. Chin. Univ., 2009, 25(5): 740-743.
[17] 宋彭生. 湿渣法在水盐体系相平衡研究中的应用 [J]. 盐湖研究, 1991, (1): 15-23. SONG P S. Application of wet residue method in study on phase equilibria of salt-water systems [J]. Journal of Salt Lake Research,1991, (1): 15-23.
[18] 苏裕光, 吕秉玲, 王向荣. 无机化工生产相图分析(一)基础理论[M]. 北京: 化学工业出版社, 1985: 136-137. SU Y G, LÜ B L, WANG X R. Phase Diagram Analysis in Inorganic Chemical Production (Ⅰ): Basic Theory [M]. Beijing: Chemical Industry Press, 1985: 136-137.
[19] KWOK K S, NG K M, TABOADA M E, et al. Thermodynamics of salt lake system: representation, experiments, and visualization [J]. AIChE Journal, 2008, 54(3): 706-727.
[20] ATBIR A, MANCOUR-BILLAH S, EL HADEK M. Solid-liquid equilibria in the quaternary system K+, Fe2+, Fe3+/Cl−-H2O at 288.15 K [J]. Fluid Phase Equilibria, 2004, 215(1): 97-103.
[21] ATBIR A, EL HADEK M, COHEN-ADAD R. Solid-liquid equilibria in the quaternary system NaCl-FeCl2-FeCl3-H2O [J]. Fluid Phase Equilibria, 2001, 181(1/2): 187-194.
[22] YIN X, YU X L, WU X Y, et al. Solubility prediction and measurement of the system KNO3-LiNO3-NaNO3-H2O [J]. Journal of Chemical & Engineering Data, 2013, 58(6): 1839-1844.
[23] SONG P S, YAN Y. Thermodynamics and phase diagram of the salt lake brine system at 25℃ (Ⅰ): Li+, K+, Mg2+/Cl−,system [J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 2001, 25(3): 329-341.
[24] YANG H T, ZENG D W, LIANG T Y, et al. Experimental determination and modeling of the solubility phase diagram of the quaternary system MgCl2+LiCl+NH4Cl+H2O at 298.15 K and its applications in industry [J]. Industrial & Engineering Chemistry Research, 2013, 52(48): 17057-17063.
[25] LI Y J, LI S N, ZHAI Q G, et al. Solubility, density, refractive index, and viscosity for the polyhydric alcohol+CsBr+H2O ternary systems at different temperatures [J]. Journal of Chemical & Engineering Data, 2013, 58(6): 1577-1588.
[26] ZHAO D D, LI S N, ZHAI Q G, et al. Solid-liquid equilibrium (SLE) of the N,N-dimethylacetamide (DMA)+MCl (M = Na, K, Rb, and Cs)+water ternary systems at multiple temperatures [J]. Journal of Chemical & Engineering Data, 2014, 59(5): 1423-1434.
[27] TABOADA M E, GRABER T A, ELIZALDE J, et al. Separation of potassium chloride from pure and industrial sylvinite by solventing-out with ammonia [J]. Informacion Tecnologica, 1996, 7(5): 41-48.
[28] GAERTNER R S, SECKLER M M, WITKAMP G. Solid phases and their solubilities in the system Na2CO3+NaHCO3+ethylene glycol+water from (50 to 90) ℃ [J]. Journal of Chemical & Engineering Data, 2004, 49(1): 116-125.
[29] PITZER K S. Thermodynamics of electrolytes (Ⅰ): Theoretical basis and general equations [J]. J. Phys. Chem., 1973, 77(2): 268-277.
[30] 李以圭, PITZER K S. 高温高压下氯化钠水溶液的热力学(Ⅰ): 在373~573 K及0.1~100 MPa条件下NaCl-H2O体系的热力学性质[J]. 化工学报, 1986, 37(1): 40-49. LI Y G, PITZER K S. Thermodynamics of aqueous sodium chloride solutions at high temperatures and pressures (Ⅰ): Thermodynamics properties over 373—573 K and 0.1—100 MPa [J]. Journal of Chemical Industry and Engineering (China), 1986, 37(1): 40-49.
[31] 李以圭, PITZER K S. 高温高压下氯化钠水溶液的热力学(Ⅱ): 在823 K及100 MPa条件下NaCl-H2O体系的热力学性质 [J]. 化工学报, 1987, 38(2): 249-255. LI Y G, PITZER K S. Thermodynamics of aqueous sodium chloride at high temperature and pressure (Ⅱ): Thermodynamic properties of aqueous NaCl to 823 K and 100 MPa [J]. Journal of Chemical Industry and Engineering (China), 1987, 38(2): 249-255.
[32] CLEGG S L, PITZER K S. Thermodynamics of multicomponent, miscible, ionic solutions: generalized equations for symmetrical electrolytes [J]. J. Phys. Chem., 1992, 96(8): 3513-3520.
[33] LI Y G, MATHER A E. Correlation and prediction of the solubility of carbon dioxide in a mixed alkanolamine solution [J]. Ind. Eng. Chem. Res., 1994, 33: 2006-2015.
[34] LI Y G, MATHER A E. Correlation and prediction of the solubility of CO2and H2S in aqueous solutions of methyldiethanolamine [J]. Ind. Eng. Chem. Res., 1997, 36(7): 2760-2765.
[35] CARNAHAN N F, STARLING K E. Equation of state for nonattracting rigid spheres [J]. J. Chem. Phys., 1969, 51: 635-636.
[36] JOHNSON J K, ZOLLWEG J A, GUBBINS K E. The Lennard-Jones equation of state revisited [J]. Molecular Physics, 1993, 78(3): 591-618.
[37] RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures [J]. AIChE Journal, 1968, 14(1): 135-144.
[38] CHEN C C, BRITT H I, BOSTON J F, et al. Local composition model for excess Gibbs energy of electrolyte systems (Ⅰ): Single solvent, single completely dissociated electrolyte systems [J]. AIChE Journal, 1982, 28(4): 588-596.
[39] PENG Q, LI Z, LI Y. Thermodynamics of potassium hydrogen phosphate-potassium dihydrogen phosphate-polyethylene glycol aqueous two-phase systems [J]. Fluid Phase Equilibria, 1994, 95: 341-357.
[40] PENG Q, LI Z, LI Y. Application of regular solution theory to calculation of liquid-liquid equilibria for water-containing systems [J]. Fluid Phase Equilibria, 1994, 97: 67-80.
[41] LU X H, MAURER G. Model for describing activity coefficients in mixed electrolyte aqueous solutions [J]. AIChE Journal, 1993, 39(9): 1527-1538.
[42] 张锁江, 韩世钧. 电解质活度系数与溶剂化数 [J]. 化工学报, 1994, 45(3): 293-297. ZHANG S J, HAN S J. Electrolytic activity coefficient and solvated number [J]. Journal of Chemical Industry and Engineering (China), 1994, 45(3): 293-297.
[43] HANSEN J P, MCDONALD I R. Theory of Simple Liquids: With Applications to Soft Matter [M]. 4th ed. Amsterdam: Elsevier, 2013.
[44] WU J Z. Density functional theory for chemical engineering: from capillarity to soft materials [J]. AIChE Journal, 2006, 52(3): 1169-1193.
[45] WU J Z. Density functional theory for liquid structure and thermodynamics [M]// LU X H, HU Y. Molecular Thermodynamics of Complex Systems. Berlin Heidelberg: Springer, 2009.
[46] ZHAO S L, LIU Y, CHEN X Q, et al. Chapter one - unified framework of multiscale density functional theories and its recent applications [M]// GUY B M, LI J H. Advances in Chemical Engineering. Pittsburgh: Academic Press, 2015: 1-83.
[47] ZHAO S, JIN Z, WU J. New theoretical method for rapid prediction of solvation free energy in water [J]. J. Phys. Chem. B, 2011, 115(21): 6971-6975.
[48] ZHAO S, RAMIREZ R, VUILLEUMIER R, et al. Molecular density functional theory of solvation: from polar solvents to water [J]. J.Chem. Phys., 2011, 134(19): 194102.
[49] ZHAO S L, LIU H L, RAMIREZ R, et al. Accurate evaluation of the angular-dependent direct correlation function of water [J]. J. Chem. Phys., 2013, 139(3): 034503.
[50] ZHAO S L, LIU Y, LIU H L, et al. Site-site direct correlation functions for three popular molecular models of liquid water [J]. J. Chem. Phys., 2013, 139(6): 064509.
[51] CUI S T, HARRIS J G. Solubility of sodium chloride in supercritical water: a molecular dynamics study [J]. J. Phys. Chem., 1995, 99(9): 2900-2906.
[52] FERRARIO M, CICCOTTI G, SPOHR E, et al. Solubility of KF in water by molecular dynamics using the Kirkwood integration method [J]. J. Chem. Phys., 2002, 117(10): 4947.
[53] KOBAYASHI K, LIANG Y, SAKKA T, et al. Molecular dynamics study of salt-solution interface: solubility and surface charge of salt in water [J]. J. Chem. Phys., 2014, 140(14): 144705.
[54] SANZ E, VEGA C. Solubility of KF and NaCl in water by molecular simulation [J]. J. Chem. Phys., 2007, 126(1): 014507.
[55] ZENG D W, LIU H X, CHEN Q Y. Simulation and prediction of solubility phase diagram for the separation of MgCl2from LiCl brine using HCl as a salting-out agent [J]. Hydrometallurgy, 2007, 89(1/2): 21-31.
[56] DOCHERTY H, GALINDO A, SANZ E, et al. Investigation of the salting out of methane from aqueous electrolyte solutions using computer simulations [J]. J. Phys. Chem. B, 2007, 111(30): 8993-9000.
[57] CHATTERJEE S, NANDA A, CHOWDHURY R, et al. Mathematical modeling and simulation of solubility and ultrafiltration behavior of hemoglobin in a semi-batch module in the salting-in and -out regions [J]. Biochemical Engineering Journal, 2003, 15(1): 11-20.
[58] LI Z Q, YU X D, YIN Q H, et al. Thermodynamics metastable phase equilibria of aqueous quaternary system LiCl+KCl+RbCl+H2O at 323.15 K [J]. Fluid Phase Equilibria, 2013, 358: 131-136.
[59] YIN Q H, ZENG Y, YU X D, et al. Metastable phase equilibrium in the quaternary system LiCl+KCl+RbCl+H2O at 348.15 K [J]. Journal of Chemical & Engineering Data, 2013, 58(10): 2875-2880.
[60] 孙玉柱, 宋兴福, 汪瑾, 等. 几种卤水化学资源利用技术[C]// 2012青岛国际脱盐大会论文集. 青岛: 中国科学技术协会, 2012: 303-308. SUN Y Z, SONG X F, WANG J, et al. Several novel technologies about the utilization of brine resources [C]// 2012 Qingdao International Conference on Desalination and Water Reuse. Qingdao: China Association for Science and Technology, 2012: 303-308.
[61] 高峰, 郑绵平, 乜贞, 等. 盐湖卤水锂资源及其开发进展 [J]. 地球学报, 2011, 32(4): 483-492. GAO F, ZHENG M P, NIE Z, et al. Brine lithium resource in the salt lake and advances in its exploitation [J]. Acta Geoscientica Sinica, 2011, 32(4): 483-492.
[62] WEINGAERTNER D A, LYNN S, HANSON D N. Extractive crystallization of salts from concentrated aqueous solution [J]. Industrial & Engineering Chemistry Research, 1991, 30(3): 490-501.
[63] TABOADA M E, GRABER T A, CISTERNAS L A. Sodium carbonate extractive crystallization with poly(ethylene glycol) equilibrium data and conceptual process design [J]. Industrial & Engineering Chemistry Research, 2004, 43(3): 835-838.
DOI:10.11949/j.issn.0438-1157.20151172
中图分类号:TQ 013.1
文献标志码:A
文章编号:0438—1157(2016)02—0379—11
基金项目:国家高技术研究发展计划项目(2011AA06A107);化学工程联合国家重点实验室开放课题项目(SKL-ChE-13C04);上海青年科技启明星计划A类项目(14QA140300)。
Corresponding author:ZHAO Shuangliang, szhao@ecust.edu.cn; SONG Xingfu, xfsong@ecust.edu.cn supported by the National High Technology Research and Development Program of China (2011AA06A107), the Open Project of State Key Laboratory of Chemical Engineering of China (SKL-ChE-13C04) and the Shanghai Science and Technology Committee Rising-Star Program (14QA14031300).
Progress in study on phase equilibria of salt-water systems
ZHANG Jie1, 2, SHI Xuewei1, ZHAO Shuangliang1, SONG Xingfu1, 2, YU Jianguo1, 2
(1State Key Laboratory of Chemical Engineering, East China University of Science and Technology, Shanghai 200237, China;2National Engineering Research Center for Integrated Utilization of Salt Lake Resource, East China University of Science and Technology, Shanghai 200237, China)
Abstract:The phase equilibria and phase diagrams of salt-water systems constitute the theoretical basis for chemical industry of inorganic salts. The fundamental studies on the phase equilibrium can provide firm support for the comprehensive development and utilization of salt lake salt resources. In this paper, the recent domestic and international research advances and methods on phase equilibria of slat-water systems from both experimental and theoretical perspectives are summarized. In particular, the experimental methods on the determination of phase diagrams for stable and metastable phase equilibrium systems as well as the factors which cause the change of phase interval and solid crystal type are presented. In addition, based on the up-to-date theoretical methods including thermodynamic models, statistical mechanics theories and computer simulations, the outline of their principles, current situations and possible extensions toward the investigation of stable and metastable phase equilibrium systems are introduced. Finally, the research hotspots in this domain are discussed along with the
expectations on the future development.
Key words:salt-water system; phase equilibria; phase diagrams; salt lakes resources

