动态表面张力破裂磷脂膜的分子动力学模拟
孔宪,胡晓宇,,卢滇楠,,刘铮(化学工程联合国家重点实验室(清华大学);清华大学化学工程系,北京 00084)
动态表面张力破裂磷脂膜的分子动力学模拟
孔宪1,胡晓宇1,2,卢滇楠1,2,刘铮2
(1化学工程联合国家重点实验室(清华大学);2清华大学化学工程系,北京 100084)
摘要:磷脂双层膜在生物传感器、仿生膜和生物膜反应器等领域具有广阔的应用前景。揭示磷脂膜破裂过程规律对于磷脂膜器件设计和应用具有重要的基础意义。以二棕榈酰磷脂酰胆碱(dipalmitoyl phosphatidylcholine, DPPC)和二棕榈酰磷脂酰甘油(dipalmitoyl phosphoglycerol, DPPG)作为磷脂膜组分,采用粗粒化分子动力学模拟研究了磷脂膜组成对其破裂过程的影响规律。首先建立了磷脂膜破裂动力学的临界破裂时间及临界破裂表面张力的识别方法;进而考察了磷脂膜组成对其破裂动力学的影响规律。模拟结果表明随着带负电组分DPPG含量增加,磷脂膜平均临界破裂时间延迟且分布变宽,即磷脂膜强度提高,磷脂膜破裂呈现非均匀特性。提出了描述动态表面张力作用下磷脂膜破裂过程的“动态”微观对抗理论,由该理论可预期磷脂膜的线张力随着DPPG含量提高而增强,与分子动力学模拟结果相符。为基于磷脂膜的分子器件的设计提供了数值模拟及理论依据。
关键词:DPPC/DPPG磷脂双层膜;分子模拟;磷脂膜破裂;表面张力;动力学理论
2015-07-17收到初稿,2015-08-14收到修改稿。
联系人:卢滇楠,刘铮。第一作者:孔宪(1988—),男,博士研究生。
Received date: 2015-07-17.
引 言
自然界的磷脂双层膜由两层磷脂单分子组装而成,是生命活动的重要载体[1]。磷脂膜的生物相容性使得其在生物传感器[2]、仿生纳滤膜[3]和生物膜反应器等领域呈现良好的应用前景。阐释外力作用下磷脂膜破裂过程的规律,对于磷脂膜和基于磷脂膜的器件设计及应用具有重要的基础意义。表面张力是磷脂膜所受到的最重要外力之一[4-6],磷脂膜在高强度表面张力及其快速变化作用下会加速破裂。微管吸吮实验表明,当表面张力在(10~30)× 10−5N·cm−1的范围内,磷脂囊泡就会发生破裂[7-11],磷脂囊泡破裂亦与表面张力的施加速度有关[11]。然而磷脂膜的破裂是发生在分子尺度上的微秒级变化,尚难以直接通过实验研究磷脂膜破裂的分子机制[12]。分子模拟为研究磷脂膜的破裂提供了有力工具。Tieleman等[13]利用全原子分子动力学模拟发现对于纯DPPC磷脂膜,当横向的机械拉伸力大于−200×10−5Pa时,磷脂膜会发生不可逆的破裂。Groot等[14]采用耗散粒子动力学研究了表面活性剂对张力下磷脂膜的破裂行为的影响,模拟结果显示表面活性剂的存在降低了磷脂膜的可拉伸性并且降低了磷脂膜所能承受的最大表面张力。Leontiadou 等[15]采用分子动力学的方法研究了纯DPPC膜中亲水性孔道的结构及磷脂膜的破裂,结果表明当磷脂膜的表面张力低于38×10−5N·cm−1时,膜中的亲水性孔道可以保持稳定的结构;而当表面张力大于该值时,孔道结构逐步扩大并最终导致膜的破裂。Lai等[16]的研究表明,直径小于0.5 nm的纳米粒子有助于水分子进入磷脂双分子层并诱导磷脂膜破裂;而直径大于0.7 nm的纳米粒子则有助于稳定磷脂膜。Xie等[12]采用分子动力学模拟展示了表面张力的施加速度对于纯DPPC磷脂膜破裂的影响。总体而言,从分子水平上揭示磷脂组成对磷脂膜破裂的影响机制以及对非恒定表面张力作用下磷脂双层膜的破裂规律的研究尚有待深入。
本文利用粗粒化分子动力学模拟方法,考察表面张力强度为80×10−5N·cm−1条件下磷脂膜的破裂过程。通过建立磷脂膜破裂临界时间和临界表面张力值的分析方法,采用电中性的二棕榈酰磷脂酰胆碱(dipalmitoyl phosphatidylcholine, DPPC)和带负电的二棕榈酰磷脂酰甘油(dipalmitoyl phosphoglycerol, DPPG)作为磷脂膜组分,考察表面张力施加速率以及磷脂膜组成对磷脂膜破裂行为的影响规律。进一步地,提出“动态”微观对抗理论以描述磷脂膜破裂过程的动力学,旨在为磷脂膜和磷脂膜元件的设计及其应用提供理论指导。
1 分子动力学模拟与分析
1.1模型
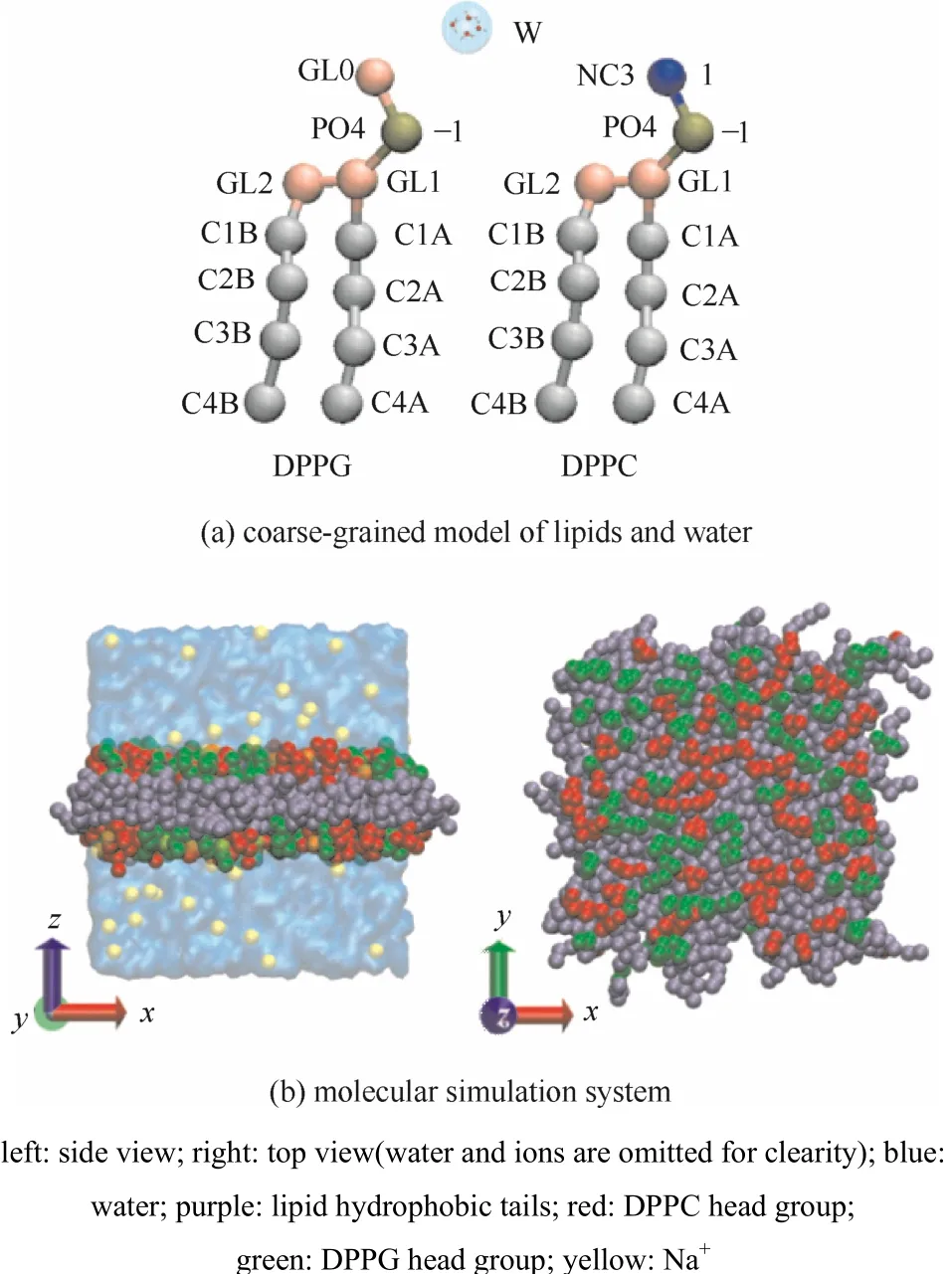
图1 磷脂双层膜模型Fig.1 Model of lipid bilayer membrane
采用Marrink等开发的Martini粗粒化力场[17-18],整个模拟系统包含粗粒化的磷脂分子、粗粒化的水粒子和用于平衡体系电荷的离子。磷脂分子的模型如图1(a)所示,DPPG和DPPC磷脂分子均由12个粗粒化粒子组成。其中,DPPC分子极性头部含有一个带正电的胆碱基团(NC3)粒子、一个带负电的磷酸基团(PO4)和两个中性的甘油骨架(GL1,GL2),总净电荷为0;而DPPG分子极性头部含有一个中性的甘油基团(GL0)、一个带负电的磷酸基团(PO4)和两个中性的甘油骨架(GL1,GL2),总净电荷为−1e。DPPG和DPPC磷脂分子的两条疏水尾均分别由4个疏水性的粒子组成,每个粒子代表实际的磷脂分子尾部的3个甲基或亚甲基。Martini力场中,4个水分子被粗粒化为1个粗粒化粒子,符号为W。模拟过程中用于维持模拟体系电中性的离子为粗粒化钠离子(Na+),包括钠离子及其水合分子,带有+1e的正电荷,直径为0.47 nm。
1.2模拟与分析方法
模拟软件为Gromacs 4.5.5[19], 所用力场为Martini粗粒化力场,模拟采用了周期性边界条件。控温方法均采用了Berendsen方法[20],耦合常数是0.4 ps。控压也采用了Berendsen方法,依据不同的表面张力施加速率,耦合常数控制在0.4~4.0 ps之间。控压方法是半各向异性的,磷脂膜的法向(即Z向)施加1.0×105Pa的恒定压力;而磷脂膜平面(即XY平面)施加恒定的表面张力。在模型构建过程中,模拟盒子边长X与边长Y相同,在XY平面上压力控制为各向同性,因此模拟盒子边长X和边长Y在模拟过程中始终相等,即Xbox=Ybox。依据标准的Martini力场,静电相互作用和Lennard-Jones相互作用的截断半径均设为1.2 nm,积分步长为40 fs。
所有的模拟体系[图1(b)]中,整个盒子有216个磷脂分子,两个磷脂单层的磷脂分子的数目及比例均一致。对于由DPPC构成的磷脂膜,在模拟体系中加入9028个溶剂粒子。对于由DPPC和DPPG构成的磷脂膜,为了保证模拟体系电中性,与DPPG数目相等的溶剂粒子被替换为钠离子(Na+)。
在模拟磷脂膜破裂过程之前,首先将模拟体系置于表面张力为70×10−5N·cm−1下,进行200 ns的模拟平衡。因为此表面张力低于磷脂膜破裂的临界值,故而磷脂膜保持完整性。选取平衡模拟最后50 ns,每隔0.1 ns选取构象,得到500个不同的初始构象,作为后续破裂过程模拟的初始构象。在磷脂膜破裂过程模拟时,将目标耦合表面张力值设定为80×10−5N·cm−1,在NPzσT系综条件下模拟36 ns,统计磷脂膜的破裂时间及其对应的临界破裂表面张力。
在模拟过程中,通过改变式(1)中控压耦合常数τP来考察表面张力变化速率对磷脂膜破裂动力学的影响。
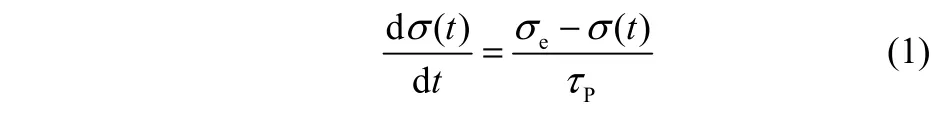
式中,σ(t)是t时刻磷脂膜的表面张力,σe是目标耦合表面张力值,τP是控压耦合常数。
结果分析过程中,采用VMD软件来观察轨迹及作图[21]。体系的表面张力(σ),盒子尺寸(Xbox, Ybox, Zbox)等是通过Gromacs自带的分析工具获取的。理论分析及拟合中用到的程序均采用Matlab来完成。
2 结果与讨论
2.1临界破裂点的判定
磷脂的临界破裂点是研究表面张力破裂磷脂膜的重要参数。为此首先考察了磷脂膜破裂过程中,磷脂双层膜的各种性质随着模拟时间的变化,结果如图2所示。
图2(a)给出了模拟盒子的X边长(Xbox)和磷脂膜法向上模拟盒子的Z边长(Zbox)随模拟时间的变化。初始构象中,磷脂膜铺满整个XY平面,因此模拟盒子边长与磷脂膜边长相等,即Xmembrane=Xbox和Ymembrane=Ybox。在磷脂膜破裂过程模拟中,X-Y平面上施加了强度为80×10−5N·cm−1的表面张力。在其作用下,磷脂膜的边长(Xbox和Ybox)以恒定的速度缓慢地变大,即磷脂膜的面积(Xbox×Ybox)逐渐增加。当磷脂膜发生破裂时,磷脂膜的边长Xbox会显著增加。磷脂膜厚度与磷脂膜法向上模拟盒子边长Zbox相关。在表面张力作用下,Zbox值缓慢降低。当磷脂膜破裂时,Zbox值会显著降低。
由于磷脂膜具有流动性,直接通过Xbox和Zbox值来判断磷脂膜是否发生破裂和相应的临界破裂压力存在误差。故求取Xbox和Zbox对时间t 的二次导数(X″box和Z″box),观察其随时间的变化,结果如图2(b)所示。结果表明,Z″box的极小值与X″box的极大值相对应,如图2(b)中绿色虚线所示。该时刻时磷脂膜尺寸变化的加速度最大,表明此时磷脂膜处于受外界合力最大的时刻,是磷脂膜破裂过程中最为剧烈的状态。标记该时刻为t′c,所对应的两个极值之间差值的绝对值为v′c,即v′c=|X″box−Z″box|。以t′c时刻为起点,向前搜索找到第一个|X″box−Z″box|≤0.02v′c的时间点,即为磷脂膜临界破裂时间点tc。绘制磷脂膜表面张力γ随时间变化曲线,结果如图2(c)所示。依据磷脂膜临界破裂时间tc,可在图2(c)中确定相应的磷脂膜临界破裂表面张力σc,如图2中洋红色虚线所示。通过对体系500次模拟案例进行统计分析,即可得到特定条件下磷脂膜的临界破裂时间tc和临界破裂表面张力σc及其统计学分布。
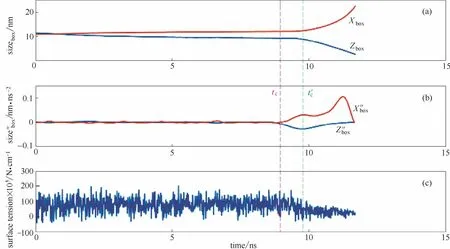
图2 磷脂膜破裂临界点的表征Fig. 2 Characterization of critical rupture point of lipid bilayer membrane (a) Xboxand Zbox; (b) second derivatives of Xboxand Zbox(X″boxand Z″box); (c) surface tension (γ)
2.2磷脂膜组成对膜破裂时间的影响
依据上述磷脂膜临界破裂时间的确定方法,计算了磷脂组成对磷脂双层膜临界破裂时间的影响。

图3 磷脂双层膜组成对临界破裂时间分布影响Fig. 3 Effects of DPPC/DPPG ratio on distribution of critical rupture time
由图3结果可知,磷脂双层膜的临界破裂时间tc均存在时间分布。随着DPPG比例增加,磷脂膜临界破裂时间分布变宽。这表明DPPG会增加磷脂膜的非均匀性,使得破裂过程随机性增强。图3结果还表明,随着DPPG比例的增加,磷脂膜的临界破裂时间会延迟。对于由DPPG构成的磷脂膜,在模拟时间内(36 ns)部分磷脂膜并没有破裂。表明DPPG有助于增强磷脂膜的结构稳定性,这对于高强度人工膜体系的设计和构建具有指导意义。DPPC和DPPG的比例分别为1:0(纯DPPC)、7:1、3:1、1:1和0:1(纯DPPG)。目标耦合表面张力值为80×10−5N·cm−1,控压偶联常数τP设定为4 ps。对于每种磷脂双层膜组成,选取了500个不同的初始结构进行模拟以进行统计平均,结果如图3所示。
2.3表面张力施加速率对磷脂膜破裂行为的影响
通过改变压力偶联常数τP来改变表面张力施加速率,研究其对磷脂膜破裂的影响,结果如图4所示。
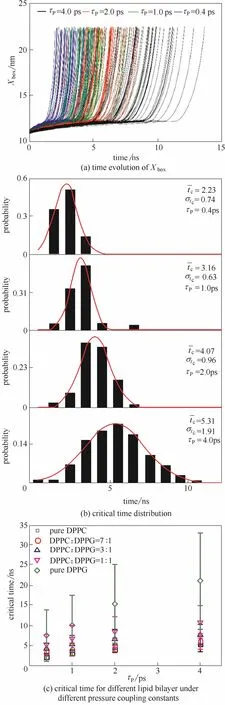
图4 不同控压耦合常数τP对纯DPPC磷脂膜破裂时间的影响Fig.4 Effects of pressure coupling constants on pure DPPC lipid bilayer’s critical rupture time
图4(a)给出了压力耦合常数τP对纯DPPC磷脂膜边长Xbox随时间变化的影响,而图4(b)给出了耦合常数τP对平均破裂时间及其分布的影响。结果表明,随着τP的增加,纯DPPC磷脂膜破裂时间显著延迟且分布变宽,即降低表面张力施加速率有助于维持磷脂膜的稳定性。这表明调整磷脂膜表面张力的施加速率是稳定或者破坏磷脂膜的可行途径,如在实际应用中可通过增大剪切力来提高细胞破裂率,而在生物膜反应器中则可通过降低流体剪切速率来维持生物膜的完整。
图4(c)给出了控压耦合常数对不同组成的磷脂膜破裂时间的影响。结果表明,随着控压耦合常数的增加,即表面张力施加速率的降低,不同组成的磷脂膜的破裂时间均增加,即增加表面张力施加速率,如高速剪切,会导致磷脂膜的快速破裂。图4(c)结果还表明,随着磷脂膜中DPPG组分的增加,控压耦合常数的影响也更加显著,即增加DPPG分子在磷脂膜中的比例有助于维系磷脂膜在高速剪切下的稳定性。这对于高稳定人工磷脂膜的设计具有指导意义。
2.4破裂过程的理论分析
微观对抗理论[22]常常用于描述在恒定表面张力作用下磷脂膜破裂比例,其假设完整磷脂膜的比例由磷脂膜的寿命常数所决定。完整磷脂膜分率Pintact随时间变化由式(2)给出
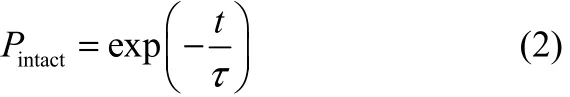
式中,τ为恒定表面张力下磷脂膜的寿命常数,t为恒定表面张力作用时间。在传统微观对抗理论中,τ值通常由表面张力σ和磷脂膜线张力Γ所决定,其关系式如式(3)所示
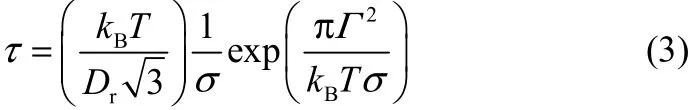
式中,Dr是一个与表面张力及线张力无关的参数,kB为Boltzmann常数,T为体系温度。
对于所模拟的体系,磷脂双层膜所受到的表面张力σ(t)是随时间而变化,因此传统微观对抗理论不适用。为解决该问题,尝试分子动力学数据来求取表面张力随时间的变化,建立“动态”微观对抗理论。
在分子动力学模拟中,磷脂双层膜所受的表面张力σ(t)可以通过式(4)求出
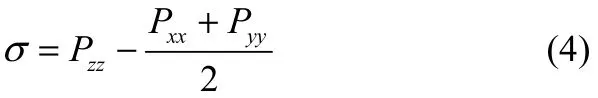
式中,Pxx、Pyy和Pzz分别为垂直于x、y、z方向上的压力分量。将式(4)代入式(1)并积分即可求得表面张力σ(t)随时间的变化
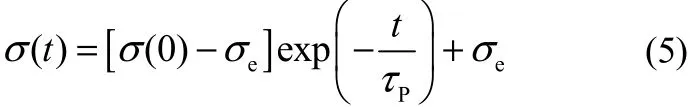
式中,σ(0)为分子动力学模拟初始时刻t=0 ns时磷脂膜的表面张力,即σ(0)=70×10−5N·cm−1;σe为目标耦合表面张力值,即σe=80×10−5N·cm−1。这里假设表面张力的变化没有松弛,可以将表面张力随时间的变化式(5)和磷脂膜寿命常数式(3)代入式(2),即可得到非恒定表面张力条件下,完整磷脂膜分率Pintact随时间变化。这样就建立了“动态”微观对抗理论方程组。
图5给出了不同磷脂组成条件下,分子模拟统计得到的完整磷脂膜分率Pintact随时间的变化,并采用“动态”微观对抗理论方程对模拟数据进行拟合。
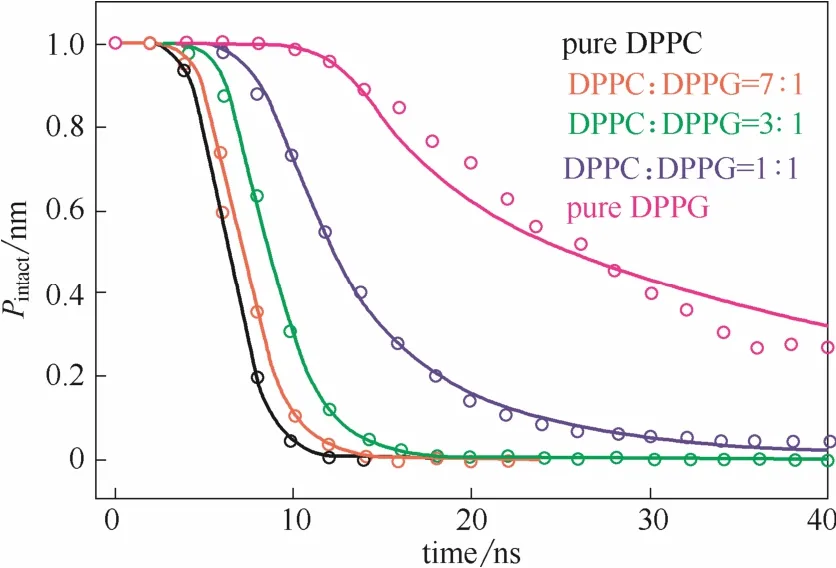
图5 不同组成的磷脂膜破裂过程的动力学Fig.5 Kinetics of rupture for lipid bilayer with different DPPC/DPPG ratio
图5中离散圆点为分子模拟统计计算得到的磷脂膜破裂过程中完整磷脂膜分率随时间变化,而连续实线为通过式(2)、式(3)、式(5)拟合得到的曲线。结果表明,所建立的“动态”微观对抗理论方程可以很好地描述不同组成的磷脂膜破裂动力学过程。通过该方程组得到不同组成磷脂膜的线张力,结果如表1所示。
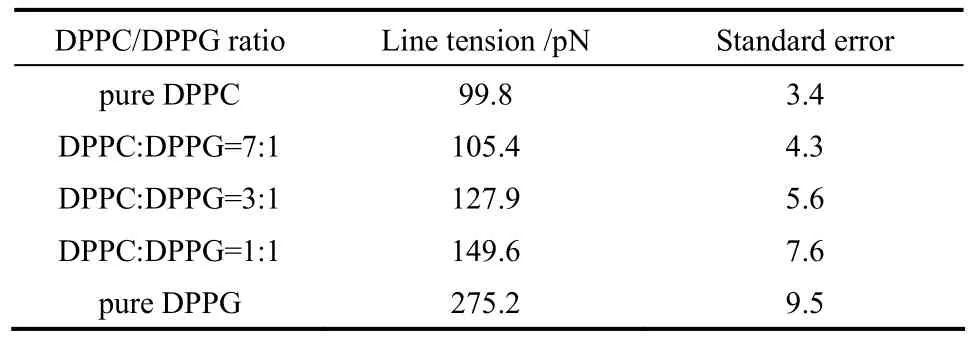
表1 不同组成的磷脂膜的线张力拟合值Table 1 Fitted value of line tension for lipid bilayer with different ratio
表1表明,随着磷脂膜中DPPG含量增加,磷脂膜的线张力也显著增加,即DPPG含量增加有助于提高磷脂双层膜的稳定性。综合图5和表1可知,“动态”微观对抗理论可以很好地描述非恒定表面张力引起的磷脂膜破裂过程,这对于外力引起的磷脂膜破裂及其调控具有理论指导意义。
3 结 论
采用粗粒化分子动力学模拟的方法研究了非恒定表面张力作用条件下,磷脂膜组成对磷脂双层膜破裂过程的影响。研究表明,提高表面张力施加速率可加速磷脂膜的破裂过程;提高磷脂双层膜中DPPG的比例,有利于增强磷脂双层膜的稳定性,具体表现为破裂时间延迟、破裂时间分布展宽和临界表面张力增加。提出了“动态”微观对抗理论模型,并对磷脂膜的破裂过程动力学进行拟合预测。结果表明该理论可以很好描述表面张力变化条件下磷脂膜的破裂过程动力学,再现分子动力学模拟结果,对磷脂双层膜的设计和应用具有指导意义。
References
[1] LIPOWSKY R, SACKMANN E. Structure and Dynamics of Membranes [M]. Amsterdam: Elsevier, 1995:201.
[2] NIELSEN C H. Biomimetic membranes for sensor and separation applications [J]. Anal. Bioanal. Chem., 2009, 395(3): 697-718.
[3] ZHAO Y, VARARATTANAVECH A, LI X S, et al. Effects of proteoliposome composition and draw solution types on separation performance of aquaporin-based proteoliposomes: implications for seawater desalination using aquaporin-based biomimetic membranes [J]. Environ. Sci. Technol., 2013, 47(3): 1496-1503.
[4] MCINTOSH T J, SIMON S A. Roles of bilayer material properties in function and distribution of membrane proteins [J]. Annu. Rev. Bioph. Biom., 2006, 35(1): 177-198.
[5] JAHNIG F. What is the surface tension of a lipid bilayer membrane? [J]. Biophys. J., 1996, 71(3): 1348-1349.
[6] SOVERAL G, MACEY R I, MOURA T F. Membrane stress causes inhibition of water channels in brush border membrane vesicles from kidney proximal tubule [J]. Biol. Cell, 1997, 89(5): 275-282.
[7] EVANS E, HEINRICH V, LUDWIG F, et al. Dynamic tension spectroscopy and strength of biomembranes [J]. Biophys. J., 2003, 85(4): 2342-2350.
[8] HEINRICH V, RAWICZ W. Automated, high-resolution micropipet aspiration reveals new insight into the physical properties of fluid membranes [J]. Langmuir, 2005, 21(5): 1962-1971.
[9] NEEDHAM D, NUNN R S. Elastic-deformation and failure of lipid bilayer-membranes containing cholesterol [J]. Biophys. J., 1990, 58(4): 997-1009.
[10] OLBRICH K, RAWICZ W, NEEDHAM D, et al. Water permeability and mechanical strength of polyunsaturated lipid bilayers [J]. Biophys. J., 2000, 79(1): 321-327.
[11] RAWICZ W, SMITH B A, MCINTOSH T J, et al. Elasticity, strength, and water permeability of bilayers that contain raft microdomainforming lipids [J]. Biophys. J., 2008, 94(12): 4725- 4736.
[12] XIE J Y, DING G H, KARTTUNEN M. Molecular dynamics simulations of lipid membranes with lateral force: rupture and dynamic properties [J]. BBA-Biomembranes, 2014, 1838(3): 994-1002.
[13] TIELEMAN D P, LEONTIADOU H, MARK A E, et al. Simulation of pore formation in lipid bilayers by mechanical stress and electric fields [J]. J. Am. Chem. Soc., 2003, 125(21): 6382-6383.
[14] GROOT R D, RABONE K L. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants [J]. Biophys. J., 2001, 81(2): 725-736.
[15] LEONTIADOU H, MARK A E, MARRINK S J. Molecular dynamics simulations of hydrophilic pores in lipid bilayers [J]. Biophys. J., 2004, 86(4): 2156-2164.
[16] LAI K, WANG B A, ZHANG Y, et al. Computer simulation study of nanoparticle interaction with a lipid membrane under mechanical stress [J]. Phys. Chem. Chem. Phys., 2013, 15(1): 270-278.
[17] MARRINK S J, DE VRIES A H, MARK A E. Coarse grained model for semiquantitative lipid simulations [J]. J. Phys. Chem. B, 2004, 108(2): 750-760.
[18] MARRINK S J, RISSELADA H J, YEFIMOV S, et al. The MARTINI force field: coarse grained model for biomolecular simulations [J]. J. Phys. Chem. B, 2007, 111(27): 7812-7824.
[19] PRONK S, PALL S, SCHULZ R, et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit [J]. Bioinformatics, 2013, 29(7): 845-854.
[20] BERENDSEN H J C, POSTMA J P M, VANGUNSTEREN W F, et al. Molecular-dynamics with coupling to an external bath [J]. J. Chem. Phys., 1984, 81(8): 3684-3690.
[21] HUMPHREY W, DALKE A, SCHULTEN K. VMD: visual molecular dynamics [J]. J. Mol. Graph Model, 1996, 14(1): 33-38.
[22] LEVADNY V, TSUBOI T, BELAYA M, et al. Rate constant of tension-induced pore formation in lipid membranes [J]. Langmuir, 2013, 29(12): 3848-3852.
DOI:10.11949/j.issn.0438-1157.20151147
中图分类号:TQ 021.4
文献标志码:A
文章编号:0438—1157(2016)02—0641—07
基金项目:国家自然科学基金项目(21276138);化学工程重点实验室基金项目(SKL-CHE-10A01)。
Corresponding author:LU Diannan, ludiannan@tsinghua.edu.cn; LIU Zheng, liuzheng@tsinghua.edu.cn supported by the National Natural Science Foundation of China (21276138) and the State Key Laboratory of Chemical Engineering (SKL-CHE-10A01).
Molecular dynamics simulation of rupture of lipid bilayer under dynamic surface tension
KONG Xian1, HU Xiaoyu1,2, LU Diannan1,2, LIU Zheng2
(1State Key Laboratory of Chemical Engineering (Tsinghua University);2Department of Chemical Engineering, Tsinghua University, Beijing 100084, China)
Abstract:The biocompatible nature of lipid bilayer makes it appealing for wide applications including biosensor, biomimetic membrane for separation or reaction. Understanding lipid bilayer rupture is of fundamental importance for the design and application of lipid bilayer based devices. In the present study, a lipid bilayer membrane made by dipalmitoyl phosphatidylcholine (DPPC) and dipalmitoyl phosphoglycerol (DPPG) was used for the molecular dynamics simulation of the lipid bilayer rupture. A method for determining the rupture time and the critical surface tension was proposed, based on which, the effects of lipid bilayer composition on the lipid bilayer rupture were examined. It was shown that an increase in the negatively charged DPPG in the lipid bilayer postponed the rupture time, indicating a strengthened structural stability. On the other hand, the widened distribution of the rupture time indicated the heterogeneous nature of the lipid bilayer. A dynamic microscopic opposing forces model was proposed to describe the above mentioned lipid bilayer rupture under an unsteady surface tension. The model had reproduced the simulation results and thus offered theoretical tools for the design and optimization of the lipidbilayer based devices and processes.
Key words:DPPC/DPPG lipid bilayer membrane; molecular simulation; lipid bilayer rupture; surface tension; kinetic theory

