基于核密度估计的极短弧定轨的分布估计方法∗
王歆 李鑫冉
(1中国科学院紫金山天文台 南京 210008) (2中国科学院空间目标与碎片重点实验室 南京 210008) (3中国科学技术大学 合肥 230026)
基于核密度估计的极短弧定轨的分布估计方法∗
王歆1,2†李鑫冉1,2,3
(1中国科学院紫金山天文台 南京 210008) (2中国科学院空间目标与碎片重点实验室 南京 210008) (3中国科学技术大学 合肥 230026)
采用分布估计算法,通过建立解空间的概率模型,实现了一种测角资料的极短弧初轨计算方法.在概率模型建立中,采用非参数核密度估计,无需对分布进行任何假设.不同于遗传算法、粒子群算法等进化算法,方法不仅考虑解的适值优劣,同时考虑了解的整体特性.根据基于实测数据的数值计算表明:方法在没有任何约束条件情况下对于一般观测精度仍可获得有效解.
航天器,天体力学:定轨,方法:数值,方法:统计
1 引言
空间目标编目的主要目的是了解在轨的工作卫星和空间碎片的准确轨道,从而可推算它们的位置,有效地支持各类航天活动.为了能够获取准确轨道必须获得足够弧长和数量的观测资料,然而随着空间目标数量的不断增加,采用面向目标的跟踪观测方式已不能满足需求.近年来空间目标观测逐步转变为面向空域的观测模式,目前我国低轨道空间目标光学测角资料超过80%来自于这种观测模式,是我国自主编目的主要数据来源.这种方式在提高观测量的同时带来了新的问题,对于每个目标每次采集的弧长是非常短的,往往只有数十秒,甚至十几秒,这么短的资料是不足以获取足够准确的轨道的,需要将许多短弧段关联在一起共同实现准确的轨道确定.通过极短弧定轨获取弧段有效信息、提高关联效率就成为一项重要的研究内容.即使在跟踪模式下,如能以较短弧长获得有效轨道显然也是有助于提高观测效率的[1].
短弧定轨问题是一个经典问题,主要困难在于问题本身的病态性,弧段越短这种病态性越突出[2].文献[3]将遗传算法(Genetic A lgorithm,GA)用于解决天基极短弧定轨问题,文献[4]采用了相同方法研究了一般的地基短弧定轨问题,但在GA算子选择上和文献[3]不同,这些工作克服了经典方法不能获得合理结果的困难,但解的偏差和弥散度仍相当大.文献[5-6]采用完全不同的优化变量、适值函数和算子给出了一种计算方案,在一定约束条件下缩小了解的偏差和弥散度,初步满足了后续应用的需求.文献[7]初步探索了采用粒子群算法(Particle Swarm Optim ization,PSO)求解极短弧定轨问题的方法,得到了和文献[5-6]相似的结果.上述工作虽然各自不同,但都采用了进化计算(Evolutionary A lgorithm),文献[8]则针对进化计算不同于经典方法的计算流程,提出了具有一般意义的资料处理策略,通过稳健估计实现了极高崩溃点的定轨.这些工作初步建立起了采用进化计算解决极短弧定轨的框架,但都需要针对具体问题进行方法、算子以及参数和约束条件的选择,而对于编目而言,面对的是大批量目标,因此过多的约束和参数并不是最佳选择.
本文从另一个角度做了探索,初轨计算的实践告诉我们,对于初轨计算而言不能以残差均方根(RMS)最小作为唯一判别.在精度范围内,短弧定轨问题是多解的,这些解的RMS十分接近,而且往往RMS最小的解并不是实际最优解[9].之前所有工作都着眼于寻找RMS最小的单个解,而忽视了解的整体情况.本文引入了分布估计算法(Estimation of Distribution A lgorithm,EDA)[10],EDA是目前国际上进化计算研究的热点之一,与GA、PSO的不同在于,EDA立足于对优势解群体的整体刻画,而并不局限于个别优势个体.
EDA仅是一个算法框架,本文基于核密度估计(Kernel Density Estim ation)实现了一种具体的算法,采用非参数方法,无需对分布进行任何假设,构造了具体的极短弧定轨方法,并结合中国科学院光学观测网的实际数据情况做了计算验证.
2 分布估计算法
EDA是进化计算领域新兴起的一类随机优化算法,是当前国际进化计算领域的研究热点,其概念最早在1996年提出并得到了迅速发展.EDA是GA和统计学习的结合,通过统计学习的手段建立解空间内个体分布的概率模型,然后对概率模型随机采样产生新的群体,如此反复进行,实现群体的进化.EDA中没有传统的交叉、变异等遗传操作,是一种全新的进化模式[11].和其他方法一样,EDA用于解决如下优化问题:
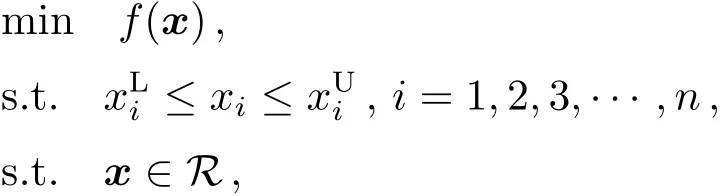
其中x=(x1,x2,···,xn)为实数域R上的n维解向量.和分别为第i维的上下界. EDA的流程如图1.EDA首先随机生成N个解作为初始种群XG={x1,x2,···,xN}, G=0为进化代数;然后依据适值优劣选择P个优势群体;接着根据优势群体构造概率模型;由概率模型通过采样,生成G+1代群体XG+1,如此迭代进化.与GA相比,EDA方法在选择优势群体后,对于优势群体内个体在建立概率模型时是等权的,因此概率模型中考虑了优势群体的数密度,是解空间整体特性和适值优劣的综合反映,这个特点非常适合极短弧定轨问题.不同的EDA实现主要区别在于概率模型建立的方法不同.
与GA一样,由于采用二进制编码比较利于概率模型的建立,EDA起初也是针对二进制编码在离散域上的优化问题,后来在此基础上发展到采用实数编码处理连续域问题.由于连续域概率模型的复杂性给设计有效的分布估计算法增加了难度,因此连续域EDA的发展相对缓慢.目前在连续域概率模型建立时基本都采用了Gauss分布假设,由于这种处理对于许多工程问题并不合适,在具体问题中直方图分布也常被使用,但直方图分布不连续光滑,也有较大局限性[12].
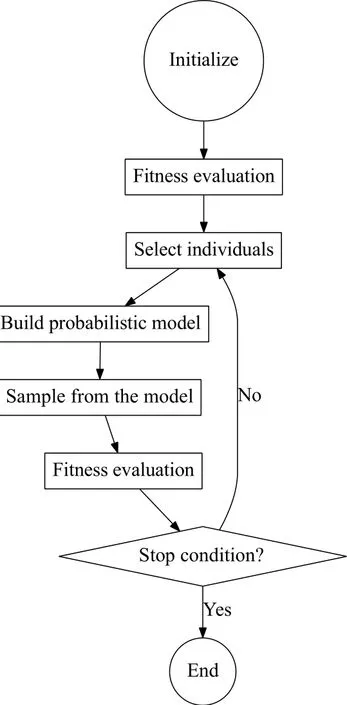
图1 分布估计算法的流程图Fig.1 T he flow chart of EDA
3 初轨计算的分布估计方法
3.1 变量和编码的选择
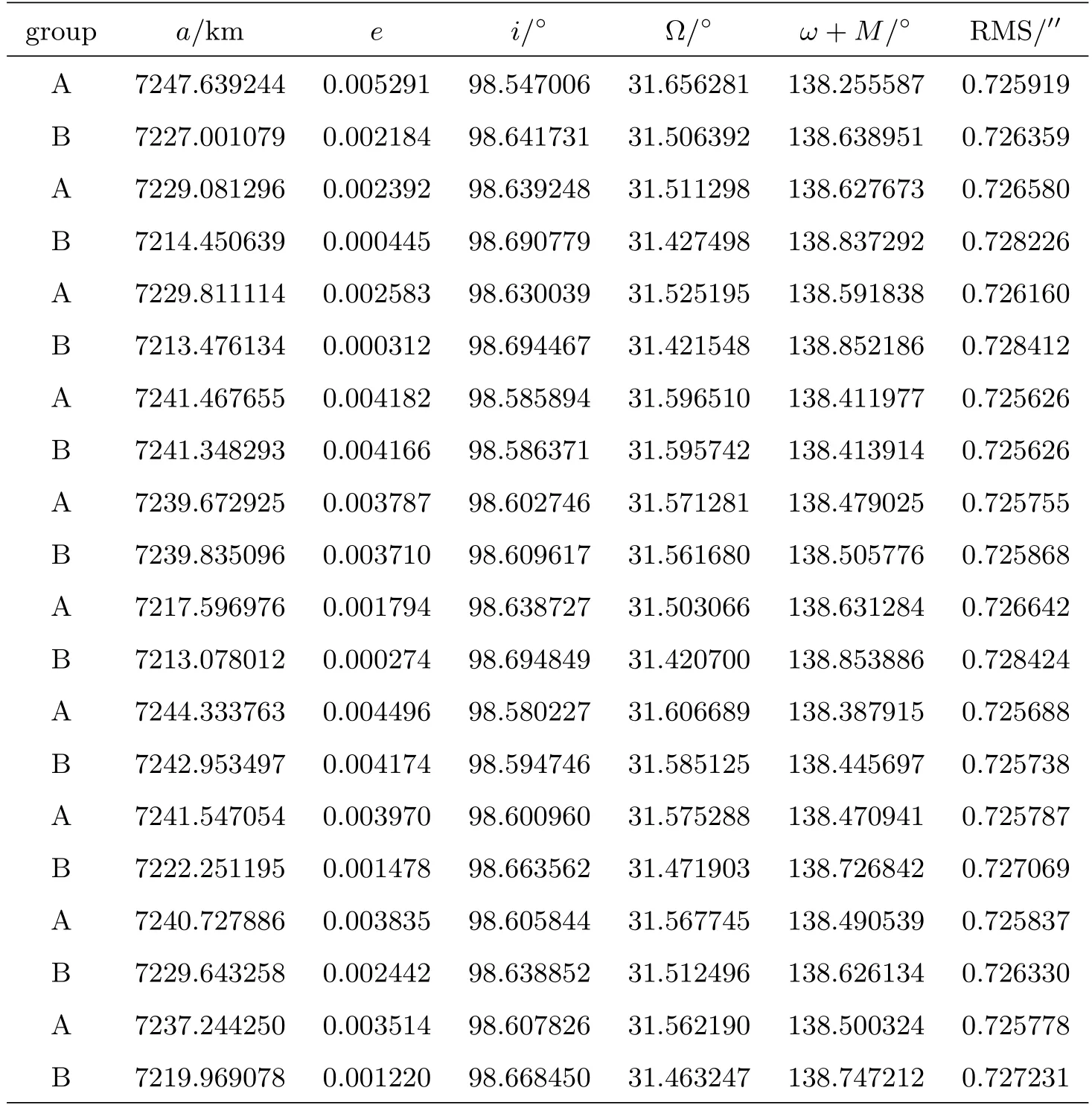
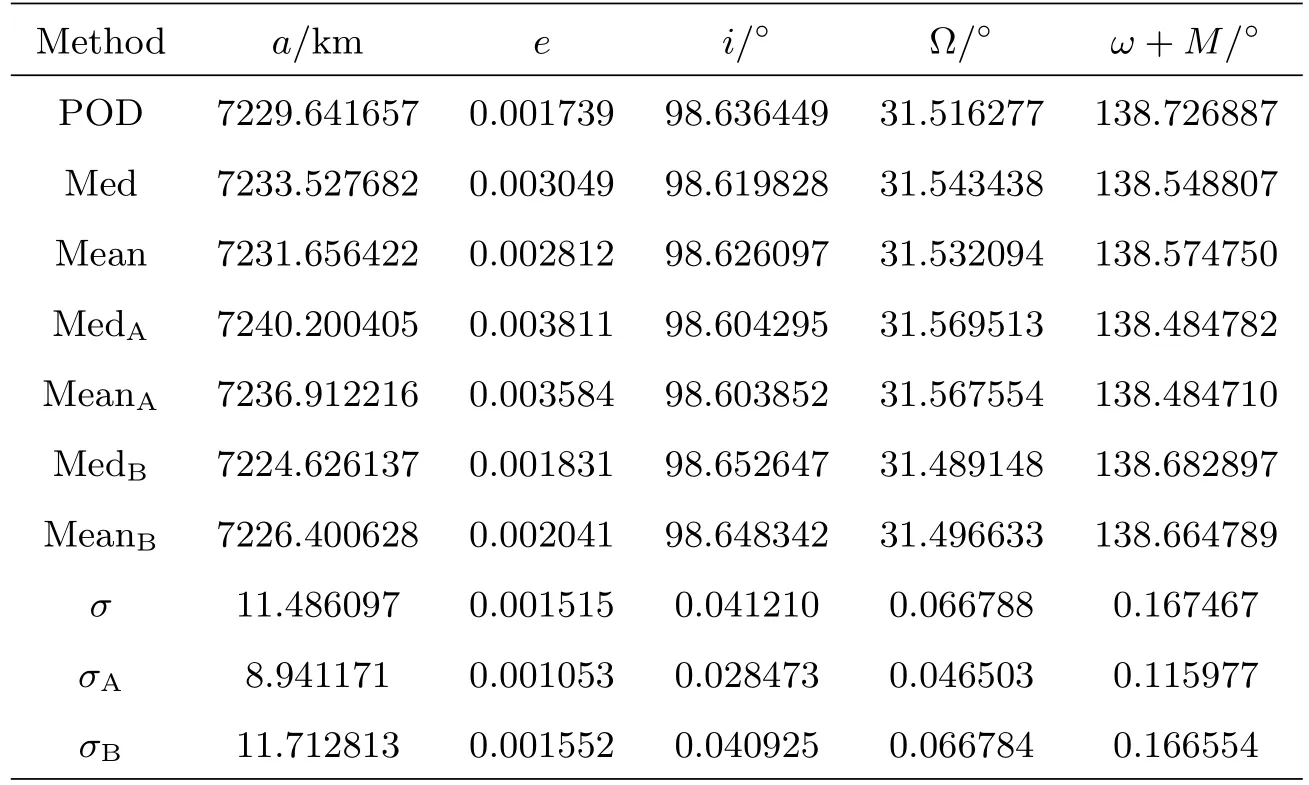
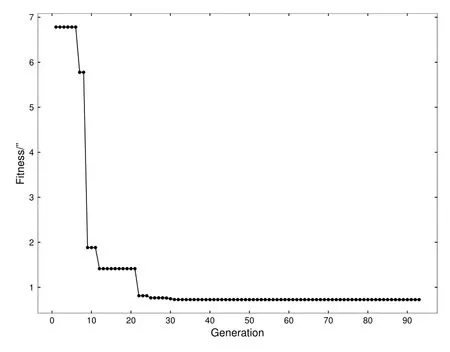
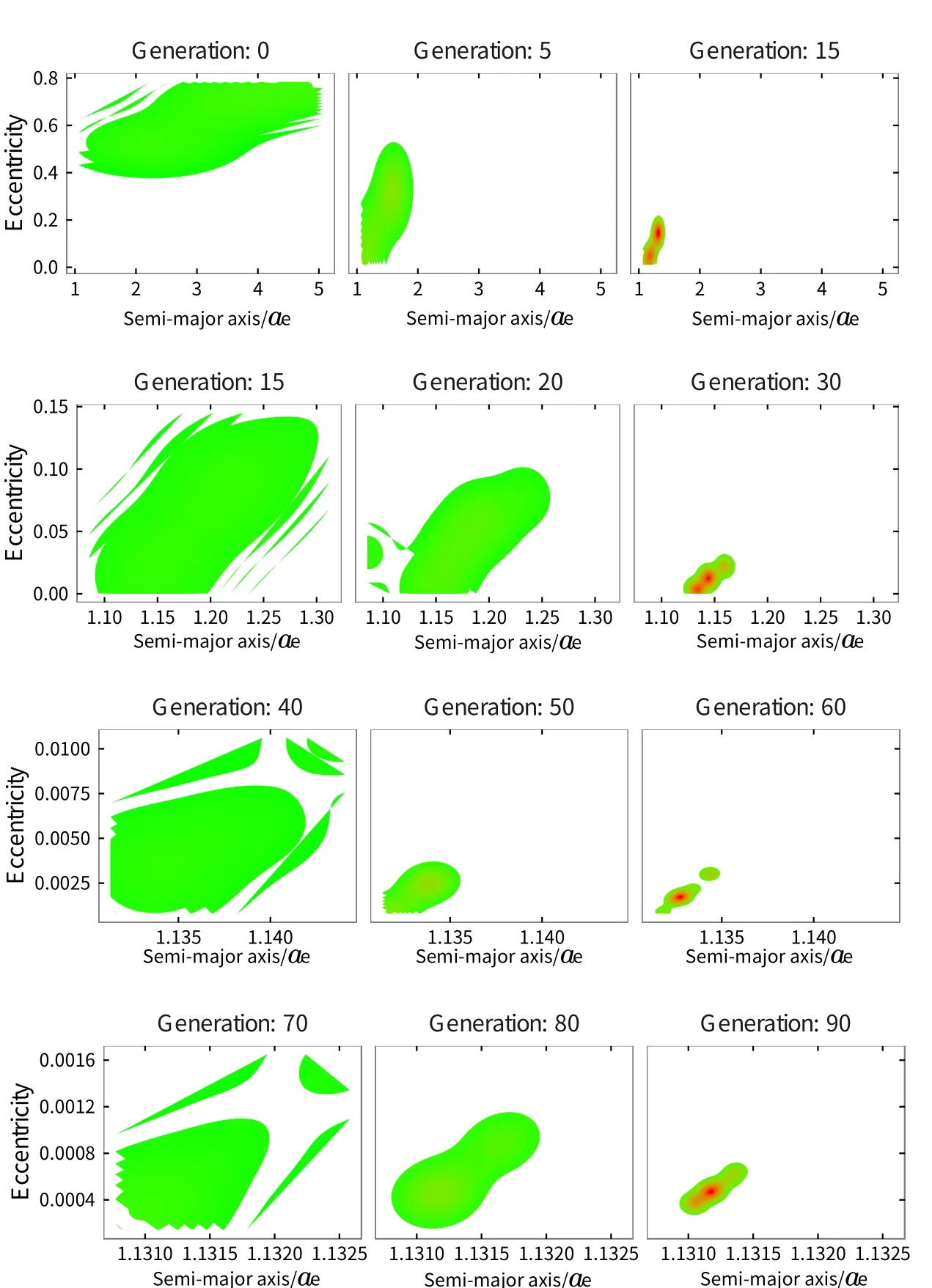
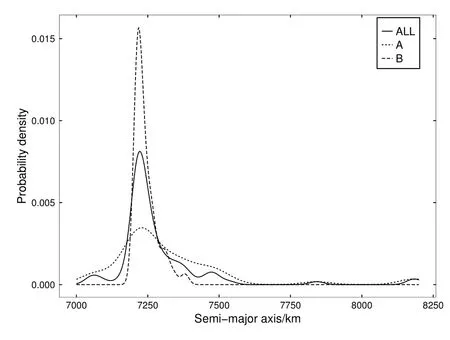
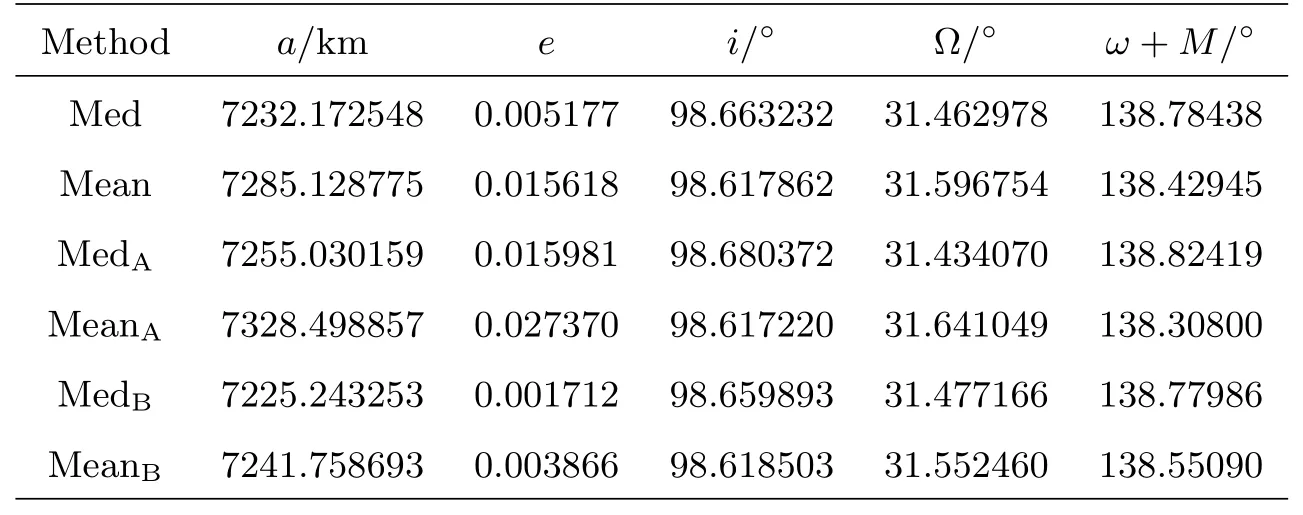
文献[3]选择观测首末时刻的斜距作为优选变量,这种选择使优选变量需要和首末观测资料共同得到轨道状态量,特别是当首末资料出现较大误差时,无法得到合理结果.文献[5-6]针对这点选择了和观测量不相关的历元时刻t0的3个Kepler根数(a,e,M0)作为优选变量,在保持参数空间维数较低的同时,使得结果不依赖于具体的某个观测量.这种选择对于近圆轨道是合适的,但当偏心率稍大时,每个优化变量都符合上下界约束条件的情况下,仍会出现a(1−e) 可见其中x1为近地点高度,确定了x1的下界,每个变量都符合上下界条件时,解都是合理的轨道.x和(a,e,M0)的逆变换是简单的. 对于定轨问题采用二进制编码使得优化空间过大,因此仍然采用了实数编码. 3.2 适值函数 采用和文献[5-6]相同的适值函数,令观测量为{ti,αi,δi,i=1,2,···,N},其中αi和δi分别为赤经和赤纬.由历元时刻t0的x经过简单转换即可得到相应的a、e、M0,任意时刻ti的平近点角M为: 此时目标斜距ρi为: 其中Ri=|Ri|,Ri为测站的地心位置矢量,Zi为目标天顶距.由测量方程可得: 对任意两个观测时刻tk、tj,tk>tj,分别得到(rk,rj),定义 适值函数为: 3.3 初值的生成 初始种群生成和一般进化计算采用的方法完全相同,对每个维在上下界取值范围内根据均匀分布随机选取.尽管取值范围并不影响计算的开展,但根据已知信息减小取值范围缩小求解空间显然是有益的.考虑到极短弧轨道计算中涉及观测时间很短,目标的地心距变化不会太大,根据圆轨道假设,任选两个观测时刻tk、tj,令rj=rk=r,由(4)–(7)式可得∆fkj,将 作为目标函数可优选得到r,这是个一维优化问题[13].显然x1不能大于r,同时考虑空间目标最低轨道高度情况,可确定x1的取值范围为[1.03ae,r].事实上远地点地心距必须大于r,但考虑到计算误差,实际取值时需要对近地点略微放大一些,而对于远地点略微缩小一些,因此没有直接采用a(1−e)和a(1+e)作为优选变量,避免了远地点近于近地点的不可行情况.这个步骤仅是参考,所以计算要求不高,一般选取首尾观测资料计算,如考虑稳健性因素可对每对观测资料做同样的优选,根据得到的全部r选取参考值. x2的取值范围对近地空间目标取[0,4ae]已涵盖了全部范围,x3∈[0,2π). 3.4 概率模型的建立方法 EDA中概率模型是根据优势群体建立的,确定优势群体规模后可采用GA的各种选择方法,由于EDA对于优势群体内个体是同等对待的,多采用截断选择或锦标赛选择.这两种方法都只涉及适值大小比较,无需对适值进行标定,算法大为简化.采用截断选择,选择适值最好的P个个体作为优势群体.利用第G代的优势群体XGE进行概率建模. 建模中将各维作为独立变量考虑,因此问题转换为3个1维建模问题.令XGE中某维数据为{y1,y2,···,yP}.不作任何分布假设,采用核密度估计方法可给出任意y的概率密度D(y)[14]: 其中h为带宽,K(·)为核函数,采用常用的Epanechnikov核函数[15]: (9)式即概率模型,令从第G代得到的优势群体建立的概率模型记为DEG,在概率模型更新过程中采用阻尼方式,第G+1代的概率模型为: 其中α为学习效率,反映了新信息的吸收率,也是旧信息的遗忘率. 对于核密度估计而言,带宽h的选择至关重要,在EDA中概率密度函数是不断收敛的,因此不宜采用固定带宽,根据Silverman大拇指法则(rule of thumb)动态选择带宽: 其中σ为建立核密度估计样本的标准差. 3.5 概率模型的采样方法 从概率模型DG中采样已无实质困难,对于核密度估计,Silverman给出了一种无需计算密度本身的采样方法[16],令数据样本为{y1,y2,···,yP},采样步骤如下:(1)从[1,P]中均匀选择一个随机整数v;(2)从K(·)中随机采样得到ϵ;(3)采样z=yv+ϵh.重复上述步骤即可得到任意样本容量的采样,新样本和原样本的概率密度函数一致.上述方法将一个非参数分布的采样问题,转换为了一个解析的参数分布采样问题,仅需要从核函数采样. 对于Epanechnikov核,有一个极其快速的采样方法[16]:生成3个[0,1)均匀分布的随机数v1、v2和v3,则采样ϵ为: 将(13)式代入上述采样过程,可快速实现从任意样本的核密度估计中采样. 3.6 终止条件 进化计算方法一般采用最大进化代数Gmax和连续C代适值没有进化作为终止条件, EDA也可采用同样的终止条件.考虑到EDA是对解的整体刻画,因此考虑概率密度收敛作为终止条件,由(12)式可知,当样本σ很小时,h趋于0,从而解不再更新.σ反映了概率密度的收敛,以样本数据在3个维度上的标准差之和σ1+σ2+σ3 EDA在进化过程中和GA一样对父代是破坏性的,GA中采用精英保留策略使得适值最好的解始终进入子代.在EDA的计算过程中记录下适值最好的结果x best作为最优解;由于EDA考虑了解的整体特征,当计算终止时,σ趋于0,说明解都集中在一点,记这个解为x prob.对于每次计算同时记录下这两个解. 3.7 (i,Ω,ω)的求解 由优选得到历元t0时刻的(a,e,M0)可求得ti时刻的地心位置矢量ri,在此基础上求解完整的6个轨道根数已无任何困难.考虑到极短弧定轨精度要求不高,由每对(ri,rj)可得到一组(i,Ω,ω),取其平均(,,)作为结果,考虑稳健性用中值替代均值作为结果. 采用MATLAB1h ttp://www.m athw orks.com编写了程序,并选取中国科学院空间目标与碎片光学观测网中的一圈实测资料进行了数值验证,设备精度优于5′′,事后验证该圈实际精度1′、采样频率1 Hz,采用了前10 s弧段做计算验证.根据圆轨道假设计算得到该弧段的地心距约为1.13ae,因此优化变量的取值范围为x1∈[1.03ae,1.15ae]、x2∈[0,4.0ae]以及x3∈[0,2π],对于a和e并未利用任何先验信息.由于EDA需要对概率密度进行估计,过少数量不利于模型的建立,因此种群大小大于其他进化算法,参数取N=100、P=30、α=0.1、Tσ=10−6. 图2给出了一次计算中适值的收敛过程,可见算法全局搜索能力强,进化开始收敛很快,30代后适值已非常接近最终结果. 初轨计算中(a,e)是最为关心的,将(x1,x2)转换为(a,e)后,图3给出了概率密度的变化情况.图中颜色越红表示概率密度越大,每行采用了相同的尺度,行与行之间尺度不同.图中可看出进化开始,解集范围很大,峰值也不明显;随着进化过程,解集范围不断缩小,峰值也越来越显著. 与其他进化计算一样,随机数对结果会产生影响,通过MATLAB中rng(shuffle)命令采用不同随机数种子计算10次,结果列于表1,对于每次计算依次给出了x best和x prob,分别用A和B表示.表2给出了这些结果的统计信息,包括全部结果的均值(M ean)、中值(M ed)和标准差(σ),以及A组和B组的分组结果,POD表示由多天多站精密定轨得到的结果作为参考标准. 表1 不同随机数种子下的定轨结果Tab le 1 The resu lts of o rb it determ ination with d ifferen t random seed s 从表1中结果可以看出:每次计算结果虽不同,同一次计算结果中A组和B组的结果也并不完全一致,但RMS都很小并且非常接近,从寻优角度可视作等价,随机数生成对计算并无实质影响,本文方法是有效的.获得的轨道结果不同则反映了极短弧定轨本身的困难.从表2的统计结果看,各组解的均值或中值非常接近,也都能满足需求,和文献[5-6]相比,在减少约束条件情况下,解的偏差更小,标准差相当,说明关于解的整体刻画对于极短弧定轨有很好的效果,在实践中可采用多次计算的均值或中值作为参考解. 对于极短弧定轨而言,测量误差影响更为显著,文献[3]强调了极高精度观测对于极短弧定轨的必要性,即使是2′′的观测误差,对结果造成的影响也是巨大的.文献[5-6]采用参数化的Bootstrap方法[17]考察了测量误差对求解的影响,采用相同方法,根据设备精度对观测资料增加5′′的随机误差后采用本文方法定轨,以不同随机数种子重复50次,解的统计结果见表3. 表2 定轨的统计结果Tab le 2 The statistical resu lts of o rb it determ ination 图2 适值的收敛过程Fig.2 T he convergence p rogress of the fitness 从表3中结果可见:和文献[3]一样,观测精度下降后,定轨受到大幅度影响.从中值和均值看,A组受到很大影响,而B组影响较小.说明以概率密度收敛位置作为解比适值最小解对于实际问题而言更优,也再次说明考察解的整体情况是十分有利的.图4给出了初轨计算最为关心的a的概率密度图,包括了全体数据以及A组和B组的结果.图中可见都是重尾形状,解释了表3中中值结果优于均值结果的原因.两组解的弥散程度都大幅度增加,相比较而言,B组相对集中,但两组的概率密度函数峰值的位置却很接近,分别为7228.928274 km和7218.417037 km,都在可接受范围内,和没有增加误差情况下相当.高精度观测对极短弧定轨显然是十分有利的,采用本文方法在一般精度情况下仍可获取有效解,以概率密度最大作为评估选取标准解则更为稳健. 图3 概率密度收敛过程Fig.3 T he convergence p rogress of the p robab ility density 图4 半长径a的概率密度Fig.4 The p robability density of sem i-m a jor ax is a 表3 增加随机误差后的结果Tab le 3 T he resu lts of orb it d eterm ination with rand om noises 综上所述,本文方法和其他进化计算方法类似,可以克服经典方法对于极短弧定轨的困难,相比于GA、PSO等进化计算方法,在减少约束条件、一般观测精度的情况下仍可获取令人满意的结果,主要得益于算法不仅考虑解的适值大小,同时考虑了解的整体分布情况.不同于其他进化算法,算法本质上不再寻找单个解,而是寻找解的区域,不断缩小解的区域最终获得结果,直观上看,就是寻找优势解最为稠密的区域.种群大小是决定进化计算效率的主要因素之一,EDA采用的种群数量要大于其他进化算法,因此计算效率较低,然而对于极短弧而言,通常观测数据不多,在当前计算能力下已可满足实践应用的需求.本文不仅是引入一种不同的计算方法,更重要的是从优势解稠密性去考虑极短弧定轨问题,拓展了研究思路. 参考文献 [1]Bennett J C,Sang J,Sm ith C,et a l.A dSpR,2015,55:617 [2]吴连大,贾沛璋.天文学报,1997,38:288 [3]Ansalone L,Cu rti F.Ad SpR,2013,52:477 [4]H inagaw a H,Yam aoka H,Hanada T.A d SpR,2014,53:532 [5]李鑫冉,王歆.天文学报,2016,57:66 [6]Li X R,W ang X.ChA&A,2017,41:undeterm ined [7]李鑫冉,王歆.飞行器测控学报,2015,34:540 [8]李鑫冉,王歆.天文学报,2016,57:181 [9]贾沛璋,吴连大.天文学报,1998,39:337 [10]Larra˜naga P,Lozano J A.Estim ation of D istribu tion A lgorithm s:A New Too l for Evo lu tionary Com pu tation.New York:Sp ringer Science+Business M ed ia,2002:3-26 [11]周树德,孙增圻.自动化学报,2007,33:113 [12]王圣尧,王凌,方晨,等.控制与决策,2012,27:961 [13]吴连大.人造卫星和空间碎片的轨道和探测.北京:中国科学技术出版社,2011:158-191 [14]Parzen E.Anna ls of M athem atica l Statistics,1962,33:1065 [15]Epanechn ikov V A.Theory of P robab ility and Its A pp lications,1969,14:153 [16]Silverm an B W.Density Estim ation for Statistics and Data Analysis.London:Chapm an and Hall, 1986 [17]E fron B,T ibshiran i R.A n In troduction to the Bootstrap.New York:Chapm an&Ha ll,1993:53-35 Estim ation of D istribu tion A lgorithm for Initial O rbit Determ ination of Too-short-arc Based on K ernel Density Estim ation WANG Xin1,2LIXin-ran1,2,3 (1 Pu rp le M oun tain Observatory,Chinese Academ y of Scien ces,Nan jing 210008) (2 K ey Labo rato ry fo r Space O bjec t and D ebris O bserva tion,Pu rp le M oun tain O bserva to ry,Chinese Academ y of Scien ces,Nan jing 210008) (3 Un iversity of Scien ce and Techno logy of China,Hefei 230026) A new approach of the initial orbit determ ination for too-short-arc with angular measurements is im plemented by building the probabilistic model in the solution space with the estimation of distribution algorithm.without any assumption of distribution,the non-parametric kernel density estimation is employed in themodel building.Themethod,unlike other evolutionary algorithms,such as genetic algorithm and particle swarm optim ization,considers the fitness as well as the characteristic of solution space.Numerical check with real observations indicates that without any constraints,the proposed technique has a good performance for themeasurements of general accuracy. space vehicles,celestialmechanics:orbit determ ination,methods:numerical,methods:statistical P135; A 10.15940/j.cnki.0001-5245.2016.06.005 2016-01-27收到原稿,2016-02-29收到修改稿 ∗国家自然科学基金项目(11373072)资助 †wangxin@pm o.ac.cn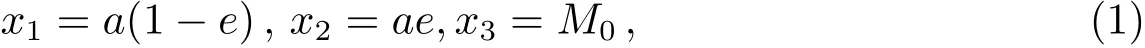
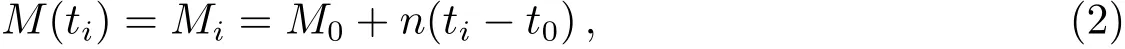

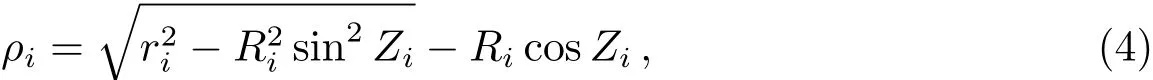
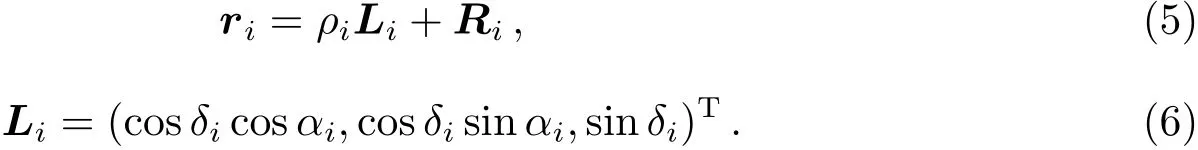

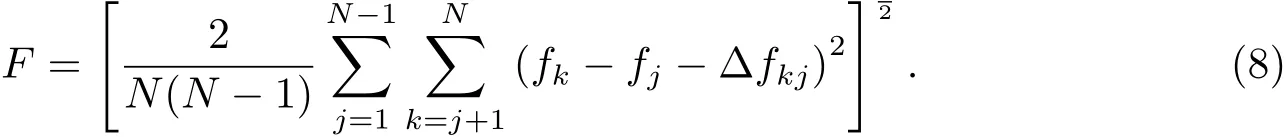
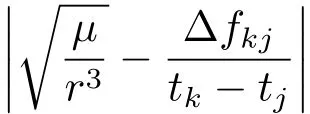
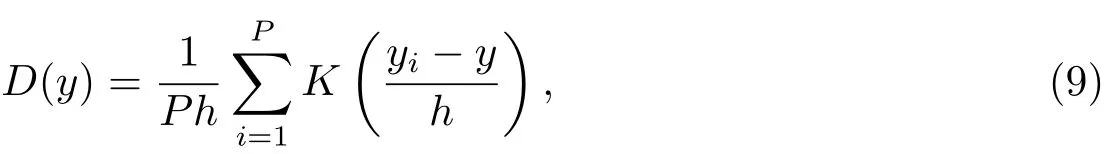
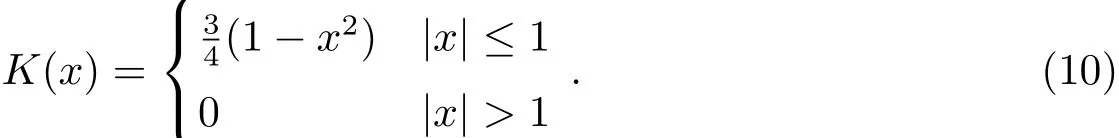
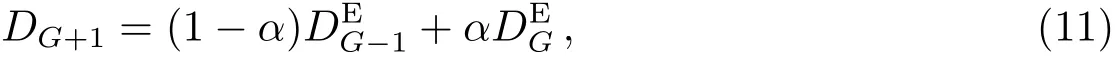

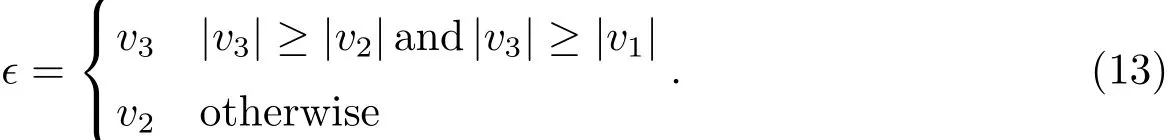
4 数值验证
5 结论与讨论

