小质量X射线双星中中子星自转演化的研究∗

徐啸天 朱浈琳

(南京大学天文与空间科学学院 南京 210093)

小质量X射线双星中中子星自转演化的研究∗

徐啸天†朱浈琳

(南京大学天文与空间科学学院 南京 210093)

为解释毫秒脉冲星自转周期的观测数据和理论结果之间的差异,采用数值分析的方法研究了小质量X射线双星中中子星的自转演化.在计算中,分别考虑了辐射压和中子星辐照引起的物质交流的不稳定性对系统的影响.结果如下:(1)吸积盘内的辐射压会使自转周期有小幅增加,中子星辐照导致的物质传输率的变化会缩短演化路径中自转减慢的阶段;(2)同时考虑辐射压和中子星辐照时在物质传输的高态阶段吸积会被辐射压抑制; (3)吸积的质量和快参数影响达到自转平衡的系统数目.

吸积,恒星:演化,恒星:中子星,X射线:双星

1 引言

在磁场强度-周期图中,脉冲星的分布表现出双峰结构(图1)[1].磁场强度在B∼1011–1012Gs范围,自转周期约为几秒的脉冲星被称为正常的脉冲星,磁场强度较弱, B∼108–109Gs,周期P 6 20 ms的脉冲星被称为毫秒脉冲星(MSPs).其分布的双峰结构表明这两种脉冲星经历了不同的演化过程.大多数MSPs存在于双星系统中,因此,一般认为MSPs为双星演化的产物[2−3].

关于MSPs形成的再循环理论认为:中子星从伴星吸积的物质会减弱中子星的磁场,同时物质所携带的角动量会加速中子星的自转[1,4−8].该过程通常发生在小质量X射线双星(LMXBs)中.

中子星的自转演化是再循环理论的一个基本问题.Ghosh等人指出中子星的吸积盘会和其磁场耦合[9−11],并产生加速或减速力矩.为描述中子星的自转随时间的演化,他们定义了“快参数”ωs(方程3),该参数与磁场强度、自转周期和光度有关.当ωs达到一个临界值ωc时,力矩消失,系统达到自转平衡,此时自转周期为平衡周期Peq.此后,许多作者研究了这个课题.Wang认为Ghosh和Lamb模型中的磁压力需要修正[12−13]; Lovelace等[14]提出磁场和吸积盘的耦合仅能发生在盘内边缘的边界层处.

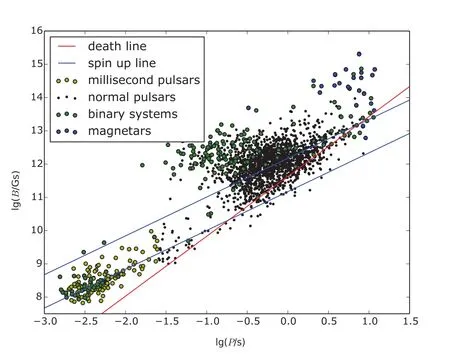
图1 脉冲星的观测分布.数据取自ATNF(A ustra lia Telescop e Nationa l Facility)脉冲星表†[1].蓝线为分别用值为1018g·s−1(爱丁顿极限)和1016g·s−1的吸积率计算得到的“加速线”(sp in-up lines).红线为用B12/P2≈0.2计算得到的“死亡线”(death line),其中B12为以1012Gs为单位的中子星磁场强度.Fig.1 O bservational d istribu tion of pu lsars.Data are taken from the ATNF pu lsar cata logue††h ttp://www.atn f.csiro.au/research/pu lsar/psrcat/psrcat help.h tm l[1].The b lue lines rep resen t the sp in-up lines calcu lated by 1018g·s−1(Edd ington lim it)and 1016g·s−1, respectively.The red line rep resen ts the death line ca lcu lated by B12/P2≈0.2,w here B12is the m agnetic field strength of neu tron stars in units of 1012Gs.

吸积中子星的磁场演化也是一个待定的问题.Romani认为吸积物质掩埋了中子星已有的磁场[15];Konar和Bhattacharya认为“欧姆耗散”可能为磁场衰减的原因:吸积物质加热了中子星的壳层,使得电导率下降,进而磁场的能量通过表面电流转化为热能[16].虽然吸积引发的磁场衰减的细节还存有争论,但是已经提出反映该过程的一些经验公式[17−19],这些作者认为吸积引发的磁场衰减仅为吸积物质质量的函数.

虽然在观测上再循环理论在不同的方面得到了支持,但仍有一些未解决的疑难.例如,观测得到的P//7总体上比理论得到的Peq//7大[20−22],其中B9是以109Gs为单位的磁场强度.这些疑难对传统的再循环理论提出了挑战.

为探索这些观测疑难背后可能的原因,应该以更自洽的方式研究LMXBs的演化过程.因此我们在上述工作的基础上,引入辐射压和中子星辐照引起的物质交流的不稳定性研究LMXBs的演化过程.本文的结构如下:第2部分介绍相关的模型;第3部分描述计算的输入参数,展示计算结果以及一些可能的解释;第4部分与观测进行比较;第5部分对工作进行讨论和总结.

2 模型

2.1 再循环理论

进入再循环阶段之前,中子星一般表现为正常的脉冲星.当系统进入吸积阶段后,由于中子星的磁场和吸积物质之间的相互作用,在中子星周围形成磁层,磁层半径Rm为磁压和物质的冲击压达到平衡的位置,Rm=ϕRA,其中ϕ≈0.5[11]、RA为阿尔芬半径, RA=3.2×1082/7(B12R36)4/7m−1/7cm,此处17为以1017g·s−1为单位的吸积率、B12为以1012Gs为单位的磁场强度、R6为以106cm为单位的中子星半径、m=M/M⊙, M为中子星质量.

在磁层中,吸积物质将沿着磁场线运动,并在极区累积造成磁场的衰减并把角动量传递给中子星.同时,吸积盘通过和磁场耦合产生力矩作用于中子星.由于磁冻结效应和磁张力的存在,与磁场耦合的区域和中子星之间发生角动量的交换,其力矩的效果依赖于盘的内边缘R0和共转半径Rco之间的关系,共转半径为开普勒转动频率和中子星自转频率相等的位置,R0和Rco之间的区域贡献加速力矩,Rco以外的区域贡献减速力矩.大约吸积0.2 M⊙质量后中子星的自转周期降至毫秒量级[23−24].

2.2 自转演化

在吸积过程中,我们采用Ghosh和Lamb提出的公式描述中子星的自转演化[11]:

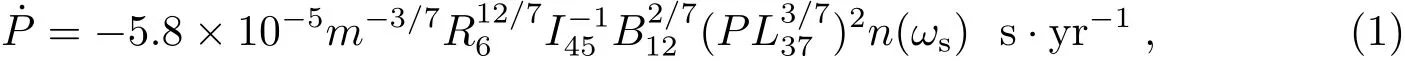
其中快参数ωs为:

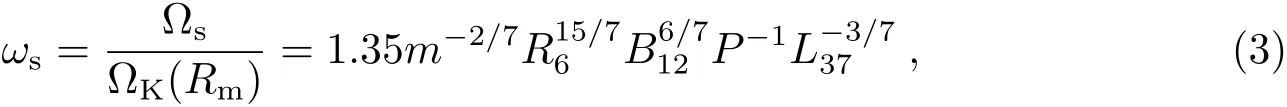
其中Ωs为中子星的自转角速度,ΩK为吸积盘中物质的开普勒速度.当ωs=ωc时,力矩消失,即P=Peq.Ghosh和Lamb[11]以及Wang[12]的工作显示ωc的范围为0.35–0.95,一些数值计算的工作显示其范围为0.5–0.7[25−26].

2.3 磁场演化

磁场的衰减和吸积质量∆M有关,我们采用Shibazaki等人提出的经验公式描述这一过程[17]:

其中Bi为初始磁场强度,Mi为常数,Mi=10−4M⊙.我们采用Zhang和Kojima提出的“底磁场强度”Bf作为计算中磁场强度的最小值[18],其定义为:

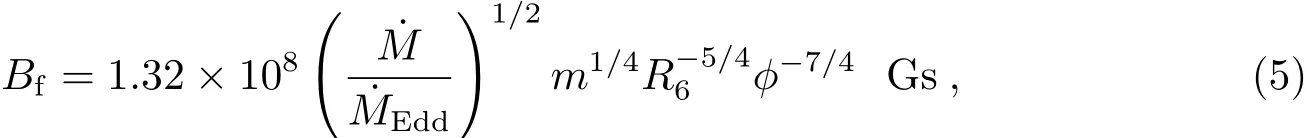
2.4 辐射压

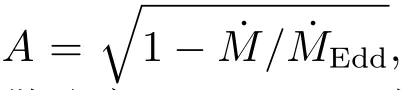
因此,ωs和的表达式也做相应的修正:

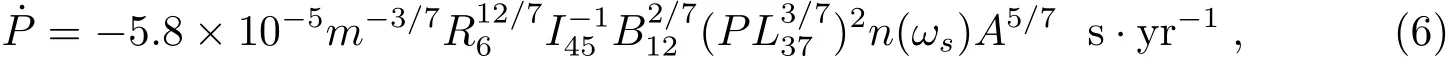
其中

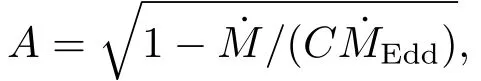
2.5 中子星辐照

在LMXBs中,由于X射线的辐照,伴星有膨胀的趋势,膨胀过程中物质传输速率提高.如果伴星始终处于洛希瓣内,则物质传输是稳定的.但是,Hameury等[29]指出物质传输的不稳定性在LMXBs中是不可避免的.对于稳定的物质传输,系统将满足以下不等式:

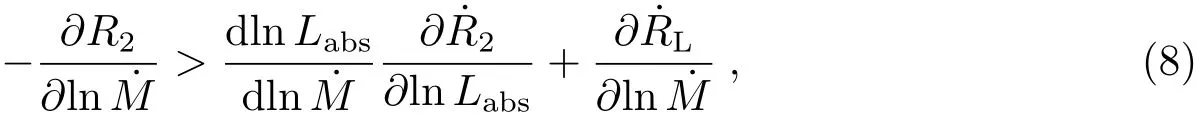
其中R2为伴星的半径,RL为洛希瓣的半径,Labs为伴星吸收X射线后再辐射部分的光度.当X射线流量和伴星质量减小时,∂2/∂ln会迅速增加,因此,该不等式很容易被破坏.

由于上述不稳定性,物质传输速率会在高态和低态之间转换.转换的周期约为1 yr至100 yr,低态可以持续一个周期的90%,其吸积率为平均吸积率的0.1%[30].在计算中,认为平均吸积率为常数,这意味着高态阶段的吸积率很容易超过爱丁顿极限,因此高态阶段的吸积率要受到爱丁顿吸积率Edd的限制.

2.6 演化路径示例

在这一部分中我们计算了LMXBs在lg P-lg B图中的演化路径.以下为输入参数:中子星的初始周期为1 s;初始磁场强度为1012Gs;质量和半径分别为1.4 M⊙和10 km;平均吸积率分别取3个值,1016、1017和1018g·s−1;ωc的值为0.5.

1.参考模型

该模型中,仅考虑吸积引起的磁场衰减(方程4)和自转周期的演化(方程1).计算结果(图2)显示,对于相对低的吸积率(=1016,1017g·s−1),系统会先经历一个减速过程(lg P-lg B图),然后加速,但ωs-lg t图显示吸积了0.2 M⊙之后未完全达到平衡.

2.考虑辐射压的模型

该模型中,考虑辐射压的效应,即用参数A修正参考模型.计算结果(图3)显示辐射压使减速阶段延长(lg P-lg B图),这是因为吸积受到了来自中子星的辐射压的抑制,物质的运动为亚开普勒,即物质携带的角动量有一定减小.另外,ωs-lg t图显示辐射压不会显著地影响ωs的演化.

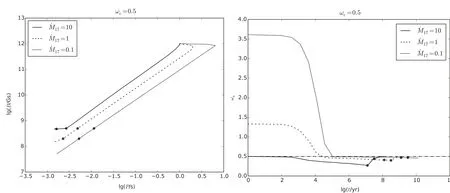
图2 由参考模型计算的结果.左图显示了系统在lg P-lg B图上的演化轨迹;右图显示了系统在ωs-lg t图上的演化轨迹,即力矩的变化.实线、虚线、点线分别代表17=10,17=1和17=0.1的情况.线上的两个实点分别表示∆M=0.2M⊙和∆M=0.5M⊙.点虚线表示ωs=0.5.图3–6的图例和本图一致.Fig.2 Calcu lated resu lts in the referenced m odel.T he left panel show s the evolu tion tracks in the lg P-lg B d igram.The righ t panel show s the evo lu tion tracks in theωs-lg t d igram.The so lid,dashed,and dotted lines rep resen t the resu lts with17=10,17=1,and17=0.1,resp ectively.T he tw ofilled circles rep resent the points w here∆M=0.2M⊙,and∆M=0.5M⊙,respectively.The dashed line rep resen tsωs=0.5.Sam e in Figs.3–6.

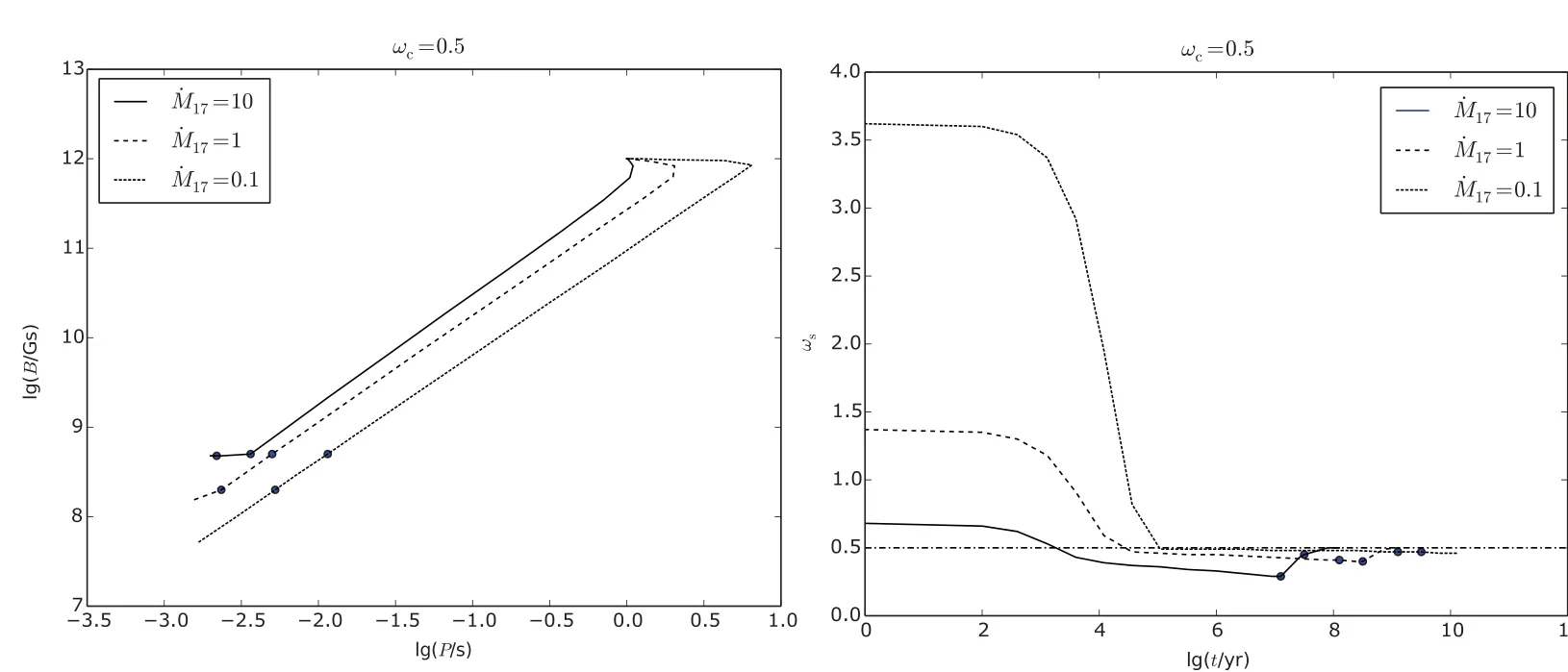
图3 考虑辐射压的计算结果Fig.3 Ca lcu lated resu lts in the m odel tak ing accoun t of rad iation p ressu re

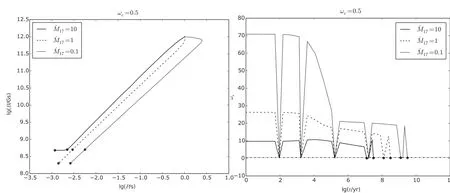
图4 考虑物质传输周期的计算结果Fig.4 Ca lcu lated resu lts in the m odel tak ing account of m ass transfer cycles

4.考虑所有效应的模型

该模型中,在参考模型的基础上考虑所有效应,并取C=2.计算结果(图5)显示高吸积率的演化路径会向低吸积率的路径偏移(lg P-lg B图),因为此时高态阶段的吸积受到了爱丁顿极限的限制.总体上,对于较高的平均吸积率,加速力矩被削弱;对于较低的平均吸积率,这些效应没有显著的影响.

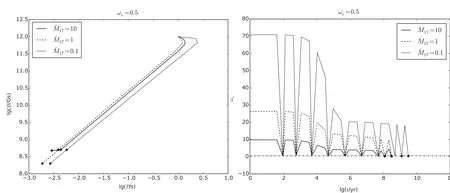
图5 考虑所有效应的计算结果Fig.5 Ca lcu lated resu lts in the m odel tak ing accoun t of a ll effects

3.考虑辐照的模型

该模型中,考虑X射线辐照造成的不稳定性引起的物质传输速率的变化.计算结果(图4)显示吸积率的变化使减速阶段缩短(lg P-lg B图),并使得ωs在ωc和大于ωc之间交替变化.

改变C的值为1.1以考察参数C对系统的影响.计算结果(图6)显示,C变小时对力矩削弱的效果会比C=2的情况更强.

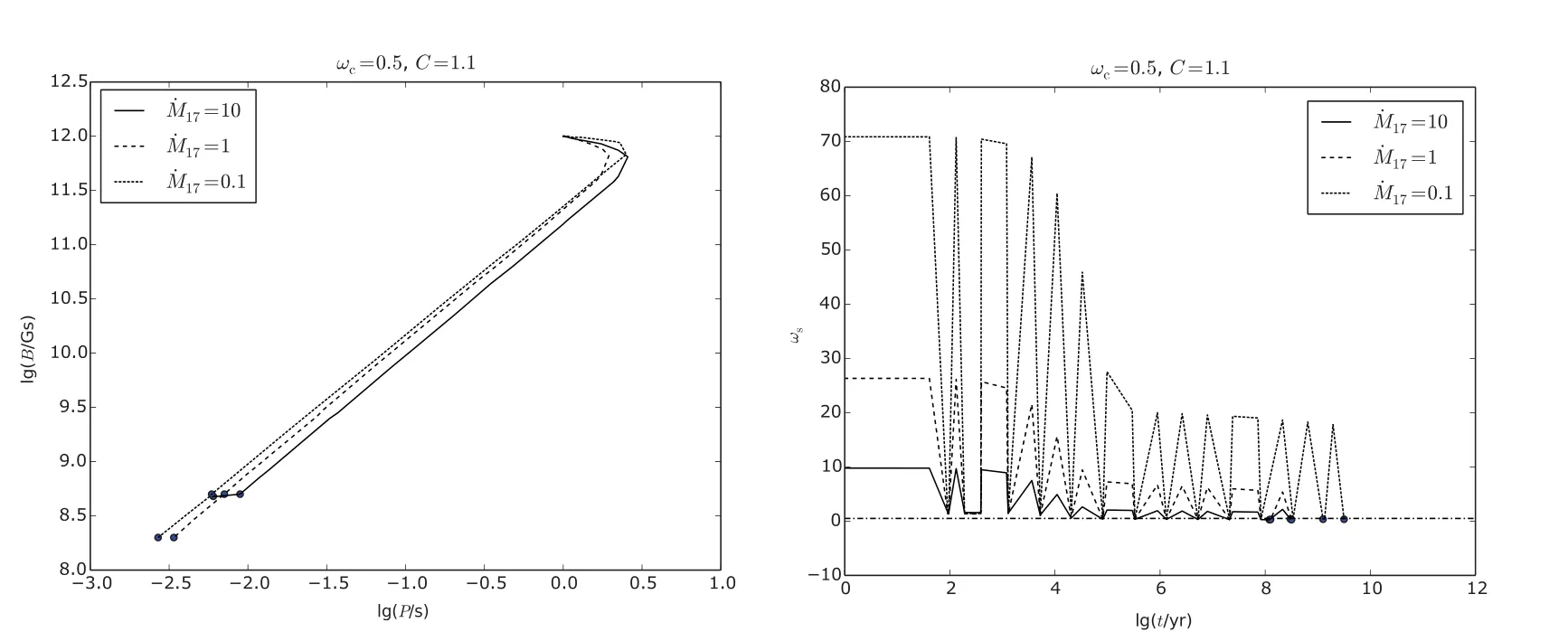
图6 C=1.1时,考虑所有效应的计算结果Fig.6 Calcu lated resu lts in the m odel taking account of all effects with C=1.1

3 大样本计算

3.1 输入参数

接着我们用蒙特卡洛方法计算105个LMXBs中中子星的演化.根据已有的统计工作,部分输入参数可以用高斯或对数高斯函数来描述:

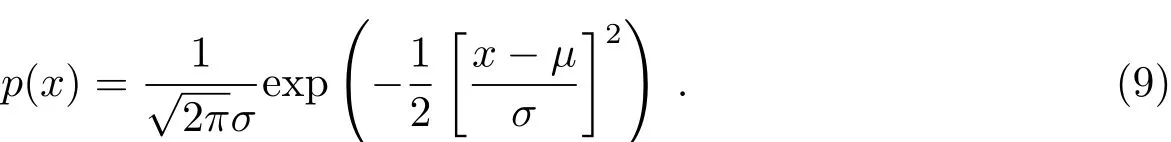
1.初始磁场强度:Bi的分布采用对数高斯分布描述,µ=12,σ=0.5,lg Bi的取值范围为10.5–14.0[31].

2.初始周期:Pi的分布采用对数高斯分布描述,µ=0,σ=0.4,Pi的取值范围为0.1 s–30 s[31].

4.中子星质量:M的分布采用高斯分布描述,µ=1.4M⊙,σ=0.2M⊙[33],M的取值范围为0.9 M⊙–2.2 M⊙.

5.中子星半径:设置中子星半径为10 km.

6.物质传输速率变化周期:取100 yr为一个周期,其中低态持续一个周期的90%,其吸积率为平均吸积率的0.1%,即low=/1000,高态的吸积率为high=(1−0.9/1000)/0.1.

7.计算的终止条件:吸积结束时,大部分系统吸积0.1–0.2 M⊙[34],少数系统吸积0.5M⊙[35].计算中取0.2 M⊙为计算的终止条件.

3.2 计算结果

3.2.1 lg B的分布

由于方程(4)显示磁场的演化仅依赖于吸积质量,并且以上大样本计算中的终止条件都为0.2 M⊙,所以这些计算得到的lg B的分布相同,图7的左图为lg B的分布,右图为底磁场强度lg Bf的分布.lg Bf的分布接近于高斯轮廓,与lg B的分布明显不同,说明0.2 M⊙不足以让一些系统达到底磁场强度(见2.6节中的示例).

图7 左图为∆M=0.2M⊙时磁场强度的理论分布;右图为方程(5)得到的底磁场强度的分布.Fig.7 T he left panel show s the theoretical d istribu tion of the m agnetic field strengths w here∆M=0.2M⊙.T he righ t panel show s the d istribu tion of the bottom m agnetic field strength ca lcu lated by Eq.(5).

3.2.2 lg P的分布

自转周期的演化由方程(6)控制.快参数是自转演化中的重要参数,其大小决定了力矩的效果为加速还是减速,当系统达到平衡周期时,ωs=ωcA.因此,ωc的值决定了平衡周期的大小.以下结果为不同的模型对中子星自转演化的影响.

1.参考模型该模型中,仅考虑吸积引起的磁场衰减(方程(4))和自转周期的演化(方程(1)).图8为计算结果,图9为lg Peq的分布.通过比较发现lg P和lg Peq的分布不同,即许多系统没有达到自转平衡(见讨论).

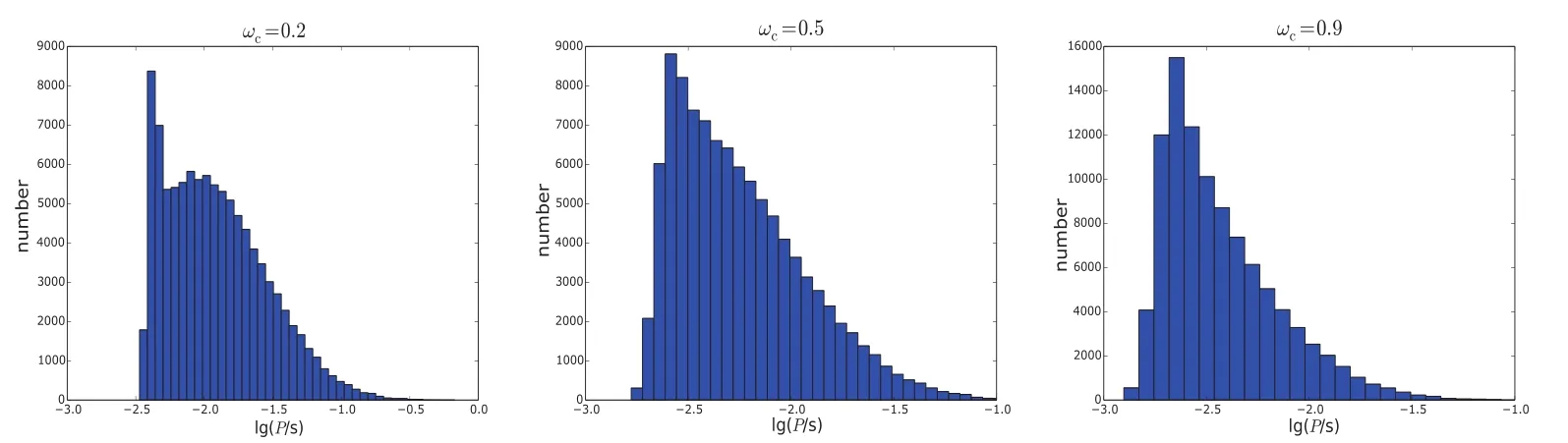
图8 由参考模型计算得到的lg P分布.左、中、右图中ωc分别取0.2、0.5、0.9.图9–12的图例和本图一致.Fig.8 Calcu lated d istribu tions of lg P calcu lated in the referenced m odel.In the left,m idd le,and righ t panels,ωcis taken to be 0.2,0.5,and 0.9,resp ectively.Sam e in the Figs.9–12.

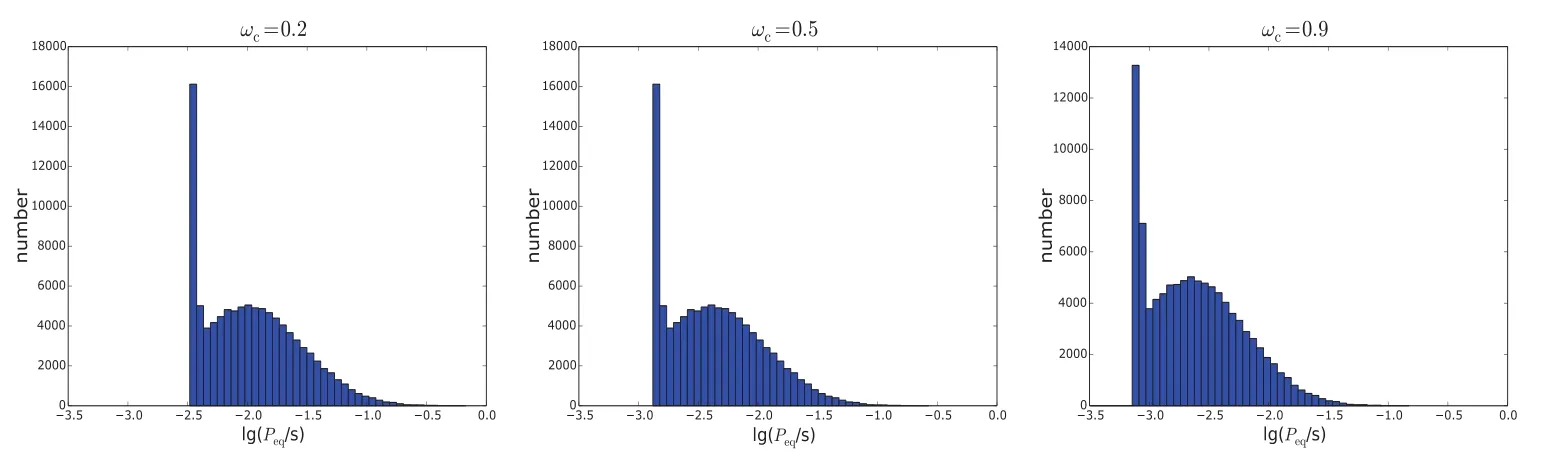
图9 lg Peq的分布Fig.9 T he d istribu tions of lg Peq

2.考虑辐射压的模型

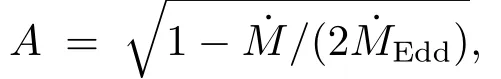
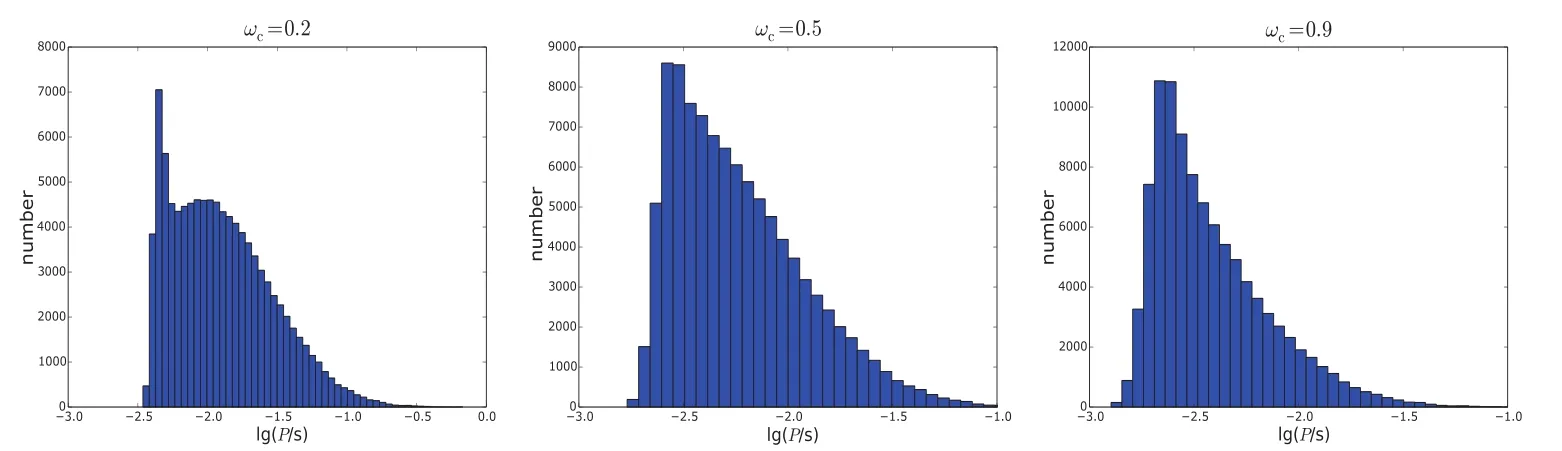
图10 考虑辐射压的计算结果Fig.10 Ca lcu lated resu lts in the m odel considering rad iation p ressu re

3.考虑辐照的模型

图11展示了计算结果.该模型中,考虑了吸积率的变化.因为高态阶段的吸积率大约为平均吸积率的100倍,很容易超过爱丁顿吸积率,当这种情况发生时,我们令其值等于爱丁顿吸积率.虽然高态仅占一个周期的10%,但高态主导了系统的演化,若仅靠低态的贡献,一些系统中中子星的自转周期无法达到毫秒量级.计算结果显示lg P的分布较参考模型更加集中,峰值位置变化不大,但峰值处对应的系统数目有所增加.

4.考虑所有效应的模型

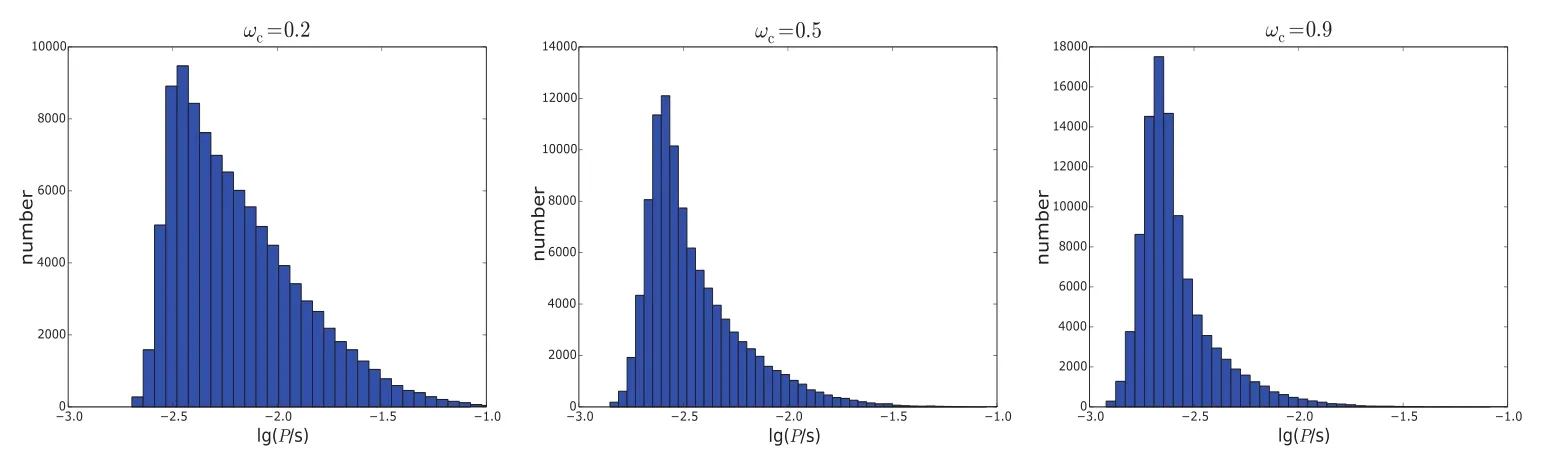
图11 考虑中子星辐照的计算结果Fig.11 Calcu lated resu lts in the m odel taking account of the irrad iation of NS

图12 考虑所有效应的计算结果Fig.12 Calcu lated resu lts in the m odel tak ing accoun t of all physica l p rocesses

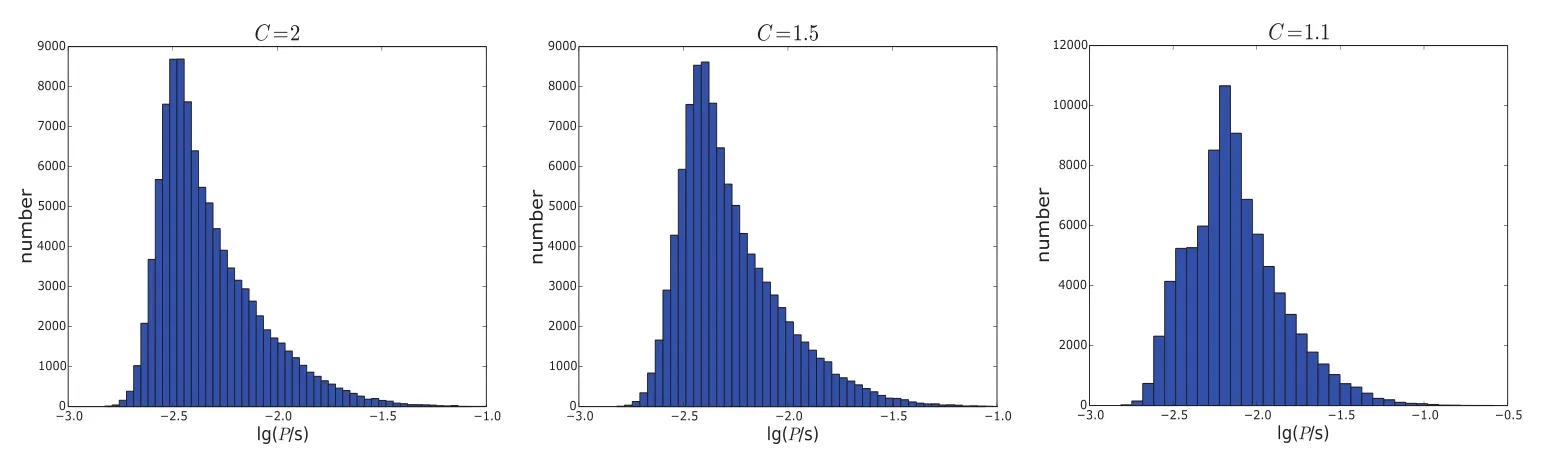
图13 改变参数C考虑所有效应并取ωc=0.5时的计算结果.左、中、右图中参数C的取值分别为2、1.5、1.1.Fig.13 Ca lcu lated resu lts in the m odel tak ing account of a ll effects with d ifferen t va lues of C and ωc=0.5.In the left,m idd le,and righ t panels,C is taken to be 2,1.5,and 1.1,resp ectively.

4 与观测的比较

在这部分中,我们把计算结果与毫秒脉冲星的观测数据进行比较,其中观测数据来自ATNF脉冲星表[1]中的中子星自转周期小于25ms的双星系统.

为了更全面地分析数据携带的信息,我们采用两种方法进行比较:用原始数据进行比较(M ethod-1);用归一化的数据进行比较(M ethod-2),其中归一化的数据由以下方式得到:

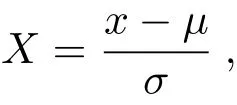
其中X为归一化的数据点,x为原始数据点,µ为原始数据的平均值,σ为原始数据的方差,即使数据的平均值为0,方差为1.Method-1是最直接的比较方法,但Method-1对数据的要求很强,我们认为使理论分布的形状和观测分布的形状一致的效应也具有一定的合理性,因此引入Method-2以比较分布函数的形状信息.以下为比较结果:

1.磁场强度

图14显示:Method-1中,在lg B<8.3的区域计算结果和观测一致,在lg B>8.3区域理论结果和观测之间有差异.M ethod-2中,理论结果和观测之间的差异仍存在.

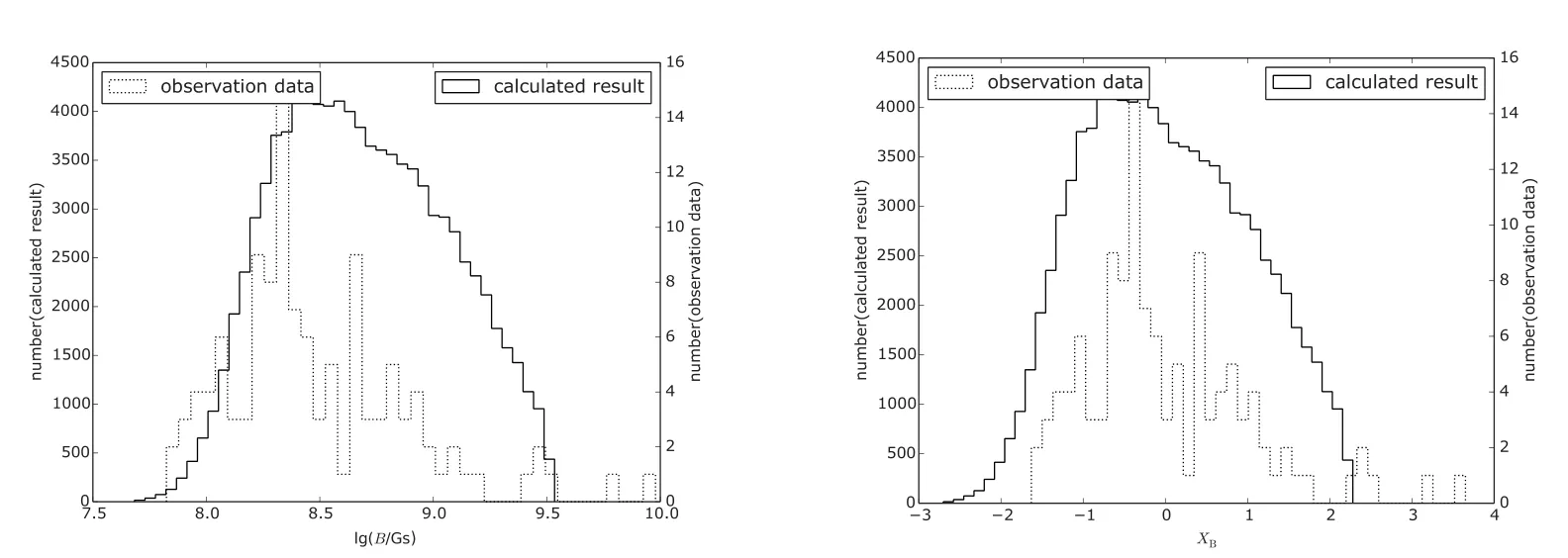
图14 磁场强度的分布.左图为原始数据lg B;右图为lg B归一化后的数据XB.Fig.14 D istribu tion of m agnetic field strengths.The left panel show s the origina l data lg B and the righ t panel show s the scaled data XB.

2.自转周期

影响lg P的分布的因素有很多(ωc、C、模型中的成分),观测数据的分布可以通过这些因素的不同组合得到解释.以下为可能的组合及其比较结果:

(1)考虑所有效应,ωc=0.5,C=2:Method-1和Method-2都显示计算结果和观测一致(图15).

(2)考虑所有效应,ωc=0.5,C=1.5:Method-1和Method-2都显示计算结果和观测一致,但峰值的位置有一些不同(图16).

(3)考虑所有效应,ωc=0.5,C=1.1:Method-1显示计算结果不能解释观测; Method-2显示计算结果和观测一致(图17).因此,一些系统的C值可能接近1.

(4)考虑所有效应,ωc=0.9,C=2:Method-1中计算结果的峰值的位置小于观测数据;M ethod-2中计算结果和观测一致(图18).

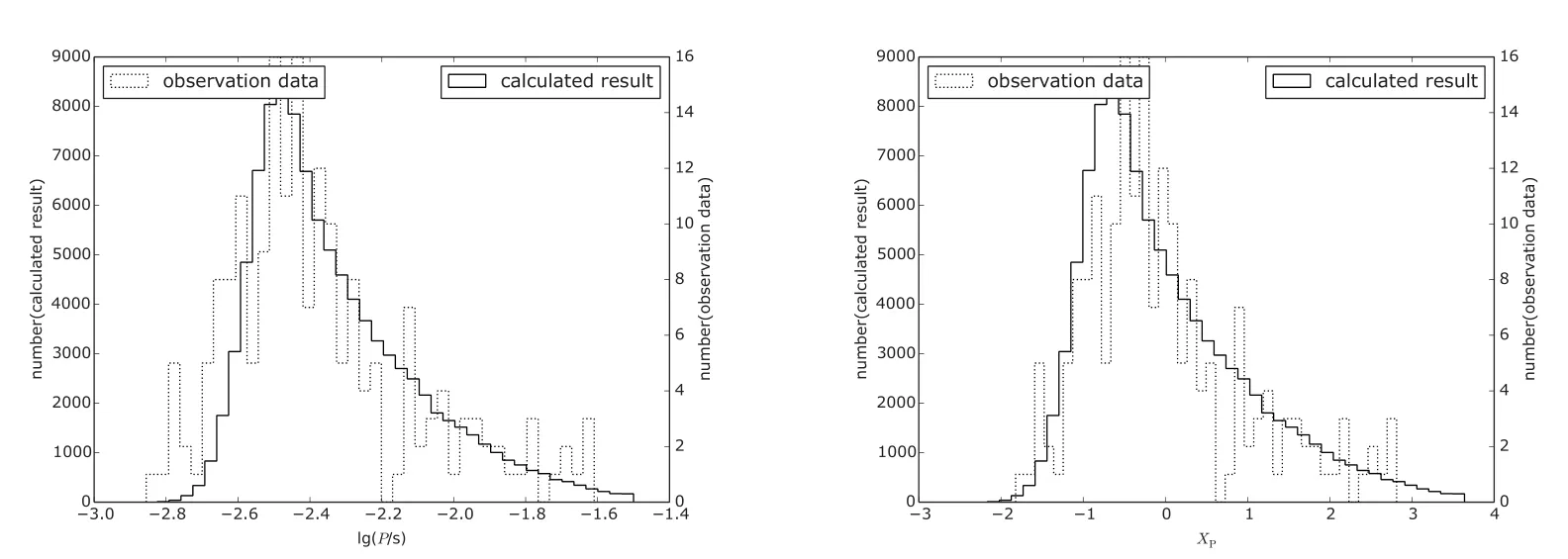
图15 由ωc=0.5和C=2得到的自转周期分布.左图为原始数据lg P;右图为lg P归一化后的数据XP.图16–19的图例和本图一致.Fig.15 D istribu tion of the sp in periods with the fo llow ing param eters:ωc=0.5 and C=2.T he left panel show s the origina l data lg P and the righ t panel show s the sca led data XP.Sam e in the Figs.16–19.

图16 由ωc=0.5和C=1.5得到的自转周期分布Fig.16 D istribu tion of the sp in p eriods with the follow ing param eters:ωc=0.5 and C=1.5

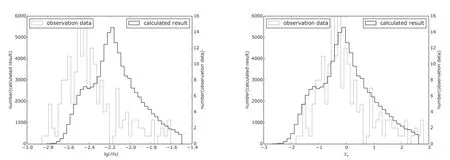
图17 由ωc=0.5和C=1.1得到的自转周期分布Fig.17 D istribu tion of the sp in periods with the follow ing param eters:ωc=0.5 and C=1.1

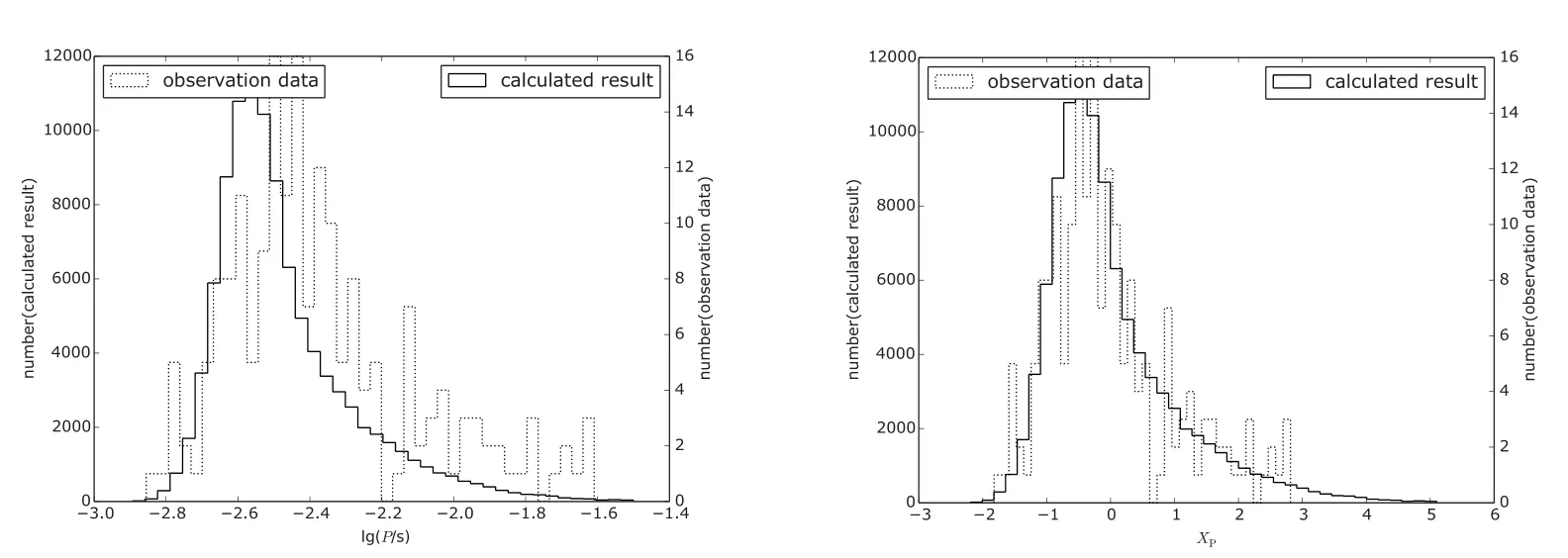
图18 考虑所有效应,由ωc=0.9,C=2计算得到的自转周期分布Fig.18 The calcu lated distribu tion of the sp in periods with the follow ing param eters:ωc=0.9 and C=2,tak ing accoun t of a ll effects

(5)考虑中子星辐照,ωc=0.9,C=2:Method-1中计算结果不能解释观测;Method-2中计算结果和观测一致(图19).因此,用中子星辐照和较高的ωc可能解释一些系统.

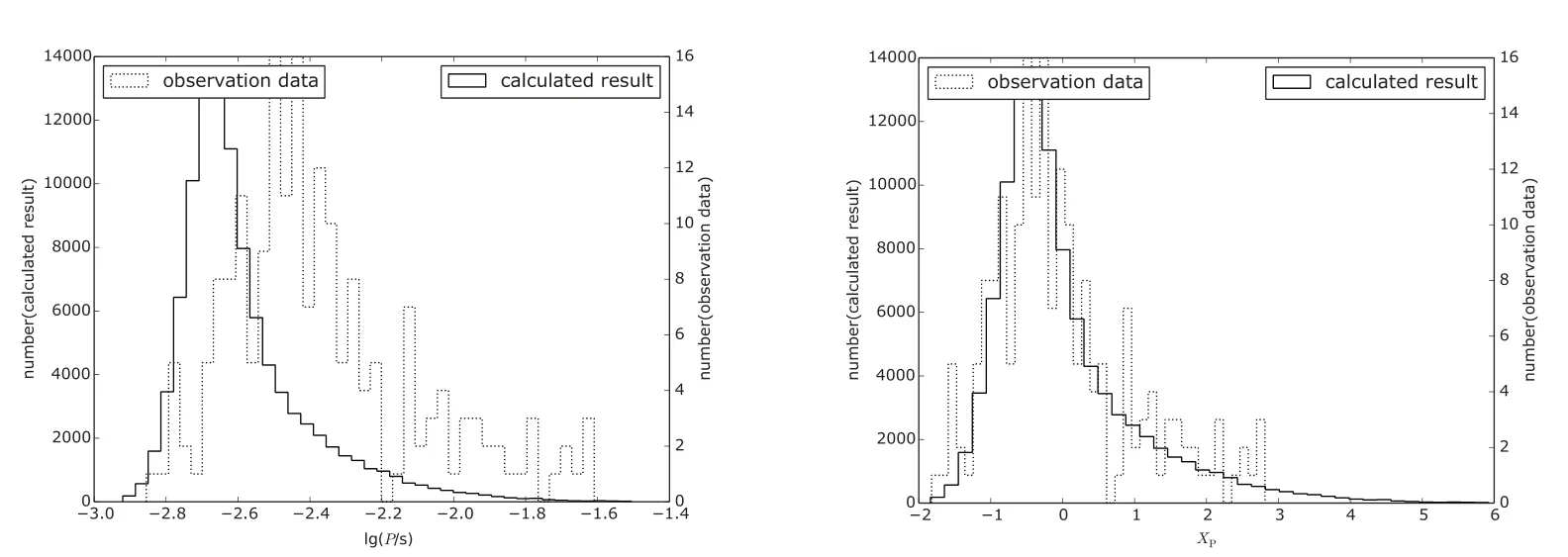
图19 考虑中子星辐照,由ωc=0.9和C=2计算得到的自转周期分布Fig.19 The calcu lated d istribu tion of the sp in periods with the fo llow ing param eters:ωc=0.9 and C=2,taking account of the irradiation of the NS

5 讨论和结论

大样本计算中参考模型的结果显示一些系统未能达到Peq,而且不同的参数空间下的结果与Peq的偏离程度也不同,这个差异与ωc相关.以下讨论中用ωs/(Aωc)来描述达到自转平衡的系统数目(达到平衡时满足ωs/(Aωc)=1).

从n(ωs)=0可以得到Peq∝ω−1c,即ωc较小的系统更容易达到平衡状态.因此ωc= 0.2时,接近平衡周期的系统数目多于ωc=0.9的情况.图20为考虑所有效应,终止条件为0.2M⊙,C=2时ωs/(Aωc)的分布.

另外,计算终止条件也会影响到达平衡的系统数目.在以上大样本计算中,终止条件都为0.2 M⊙.但实际中吸积过程可能停止于0.1 M⊙,也可能达到0.5 M⊙,我们检验了不同终止条件的影响.图21–22为取ωc=0.5,C=2,考虑所有效应时的计算结果.吸积质量越大,吸积物质携带的总角动量越多,中子星自转越快(图21),即系统更有可能达到平衡周期(图22).因此吸积质量为0.5 M⊙时接近平衡的系统数目比吸积质量为0.1 M⊙时多.

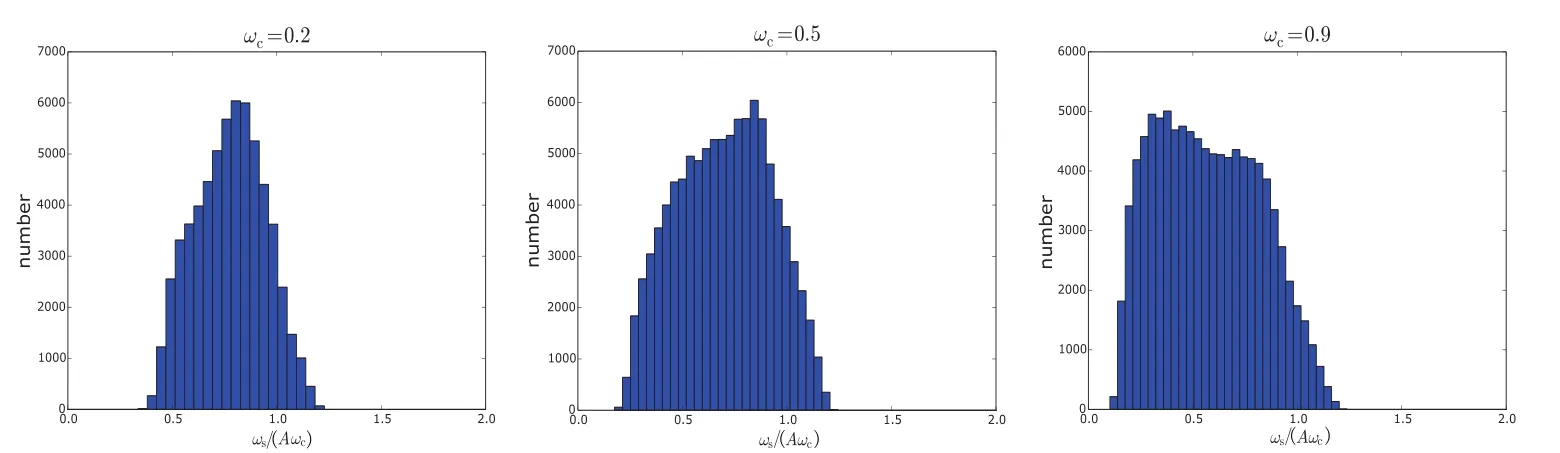
图20 ωs/(Aωc)的分布.左、中、右图中ωc分别为0.2、0.5、0.9.Fig.20 The d istribu tions ofωs/(Aωc).In the left,m idd le,and righ t panels,w e respectively useωc=0.2, ωc=0.5,andωc=0.9.

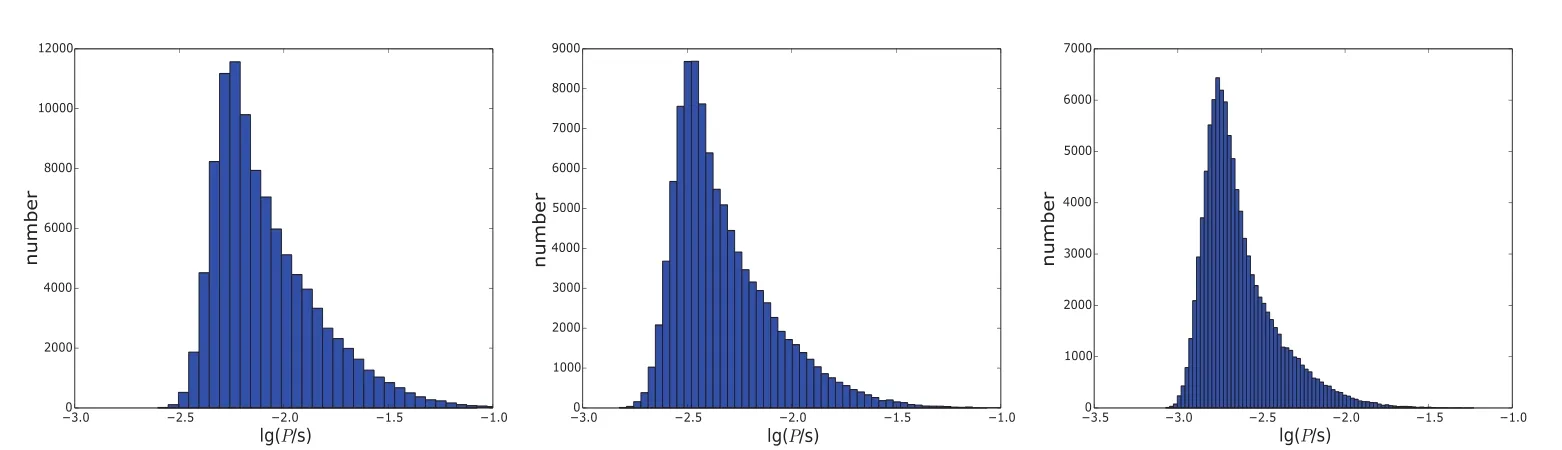
图21 改变终止条件时lg P的分布,ωc=0.5.左、中、右图中终止条件分别为∆M=0.1M⊙、∆M=0.2M⊙、∆M=0.5M⊙.Fig.21 T he d istribu tions of lg P in d ifferent term ination cond itions.In the left,m idd le,and righ t panels, w e resp ectively use∆M=0.1M⊙,∆M=0.2M⊙,and∆M=0.5M⊙as the term ination cond ition.

此次工作基于毫秒脉冲星形成理论的预言和观测之间的差异,运用蒙特卡洛模拟的方法分析了辐射压和中子星辐照对于LMXBs演化的影响.主要结果可以做如下总结:

(1)辐射压会削弱加速力矩,使自转周期有所增加.

(2)X射线对伴星的辐照会使得物质传输率在高态和低态之间转换,虽然高态持续时间很短,但主导了演化过程.对于较高的平均吸积率,它加强了加速力矩.

(4)为了描述辐射集束效应等其他因素,我们引入参数C修正了参数A的表达式.计算结果和观测的比较显示,参数C的变化范围为1–2,ωc的变化范围为0.5–0.9.

(5)计算结果显示0.2 M⊙的吸积质量不足以使大部分系统到达平衡,到达平衡的系统数目与ωc的值相关.

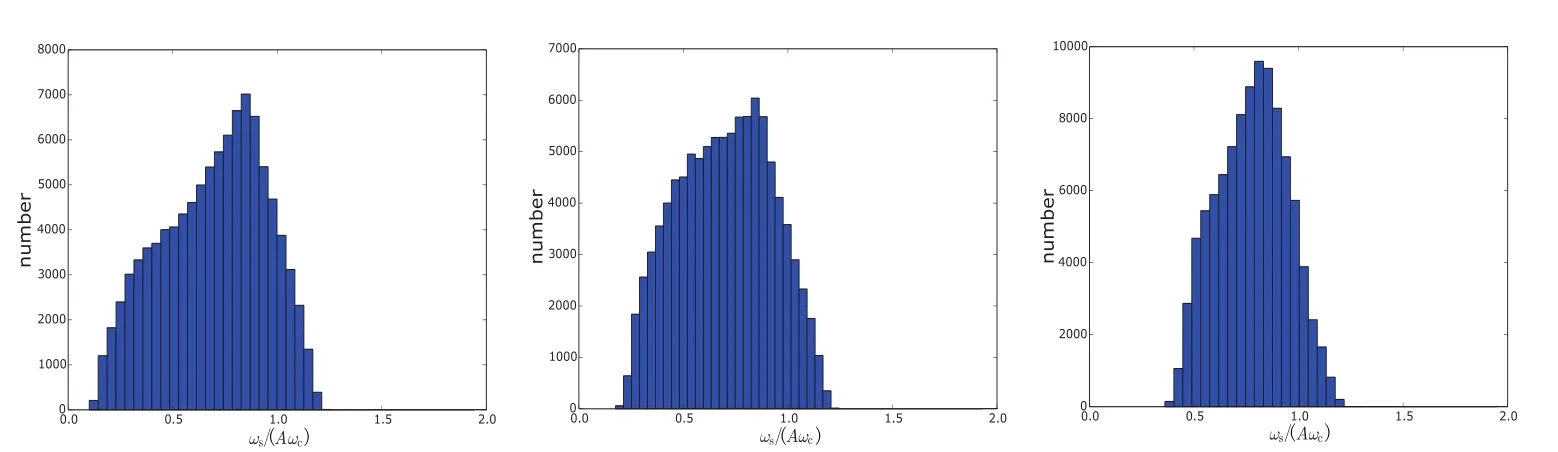
图22 改变终止条件时ωs/(Aωc)的分布.左、中、右图中终止条件分别为∆M=0.1M⊙、∆M=0.2M⊙、∆M=0.5M⊙.Fig.22 T he d istribu tions ofωs/(Aωc)in d ifferen t term ination cond itions.In the left,m idd le,and right panels,w e resp ectively use∆M=0.1M⊙,∆M=0.2M⊙,and∆M=0.5M⊙as the term ination condition.

致谢感谢南京大学李向东教授和国家天文台张承民研究员对本工作的指导和帮助.感谢审稿人对本文提出的宝贵意见.

[1]M anchester R N,Hobbs G B,Teoh A,et a l.A J,2005,129:1993

[2]Bhattacharya D,van den Heuvel E P J.PhR,1991,203:1

[3]Lorim er D R.LRR,2008,11:8

[4]A lpar M A,Cheng A F,Ruderm an M A.Natu re,1982,300:728

[5]Radhak rishnan V,Srinivasan G.CSci,1982,51:1096

[6]Taam R E,van den Heuvel E P J.A p J,1986,305:235

[7]Bhattacharya D,Srin ivasan G.X-ray B inaries.Cam b ridge:Cam b ridge Un iversity P ress,1995

[8]van den Heuvel E P J.Science,2004,303:1143

[9]Ghosh P,Pethick C J,Lam b F K.A p J,1977,217:578

[10]Ghosh P,Lam b F K.A p J,1979,232:259

[11]Ghosh P,Lam b F K.A p J,1979,234:296

[12]W ang Y M.A p J,1995,449:L 153

[13]W ang Y M.A&A,1987,183:257

[14]Lovelace R V E,Rom anova M M,B isnovaty i-K ogan G S.M NRAS,1995,275:244

[15]Rom an i R W.Natu re,1990,347:741

[16]K onar S,Bhattacharya D.M NRAS,1997,284:311

[17]Sh ibazak i N,M u rakam i T,Shaham J,et a l.Natu re,1989,342:656

[18]Zhang C M,K o jim a Y.M NRAS,2006,366:137

[19]K iel P D,Hu rley J,Bailes M,et al.M NRAS,2008,388:393

[20]Patruno A,Haskell B,D’A ngelo C.A p J,2012,746:9

[21]Shao Y,Li X D.A p J,2012,756:85

[22]Tau ris T.Science,2012,335:561

[23]程争,张承民,赵永恒,等.天文学报,2013,54:514

[24]Cheng Z,Zhang C M,Zhao Y H,et a l.ChA&A,2014,38:294

[25]Long M,Rom anova M M,Lovelace R V E.A p J,2005,634:1214

[26]Zanni C,Ferreira J.A&A,2013,550:A 99

[27]Andersson N,G lam pedakis K,Haskell B,et al.M NRAS,2005,361:1153

[28]W eng S S,Zhang S N.A p J,2011,739:42

[29]Ham eu ry J M,K ing A R,Lasota J P,et a l.A&A,1993,277:81

[30]Harpaz A,Rappap ort S.A p J,1994,434:283

[31]W ang J,Zhang C M,Zhao Y H,et al.A&A,2011,526:A 88

[32]W ijers R A M J.M NRAS,1997,287:607

[33]Zhang C M,W ang J,Zhao Y H,et al.A&A,2011,527:A 83

[34]K iziltan B,K ottas A,de Yoreo M,et al.A p J,2013,778:66

[35]van den Heuvel E P J.BASI,2011,39:1

Evolu tion of the Sp in Periods of N eu tron Stars in Low-m ass X-ray B inaries

XU Xiao-tian ZHU Zhen-lin

(Schoo l of A stronom y and Space Scien ce,Nan jing Un iversity,Nan jing 210093)

We present numerical analysis of the spin evolution of the neutron stars in low-mass X-ray binaries,trying to exp lain the discrepancy in the spin period distribution between observations of m illisecond pulsars and theoretical results.In our calculations,we take account of possib le effect of radiation pressure,and irradiationinduced instability on the structure of the disk,and the evolution of themass transfer rate,respectively.We report the follow ing resu lts:(1)Radiation pressure leads to a slight increase of the spin periods,and irradiation-induced mass transfer cycles can shorten the spin-down phase of evolution.(2)The calculated results in the m odel combining radiation pressure and irradiation-induced mass transfer cycles show that accretion is strongly lim ited by radiation pressure in high m ass transfer phase.(3)The accreted mass and the critical fastness parameter can affect the number of systems in equilibrium state.

accretion,stars:evolution,stars:neutron,X-rays:binaries

P145;

A

10.15940/j.cnki.0001-5245.2016.06.002

2016-02-11收到原稿,2016-04-01收到修改稿

∗国家级大学生创新创业训练计划项目(G1410284092)资助

†xtxuthom as@163.com