轨道距离对系外行星大气逃逸的影响∗

杨沫 郭建恒

(1中国科学院云南天文台 昆明 650011) (2中国科学院天体结构与演化重点实验室 昆明 650011) (3中国科学院大学 北京 100049)

轨道距离对系外行星大气逃逸的影响∗

杨沫1,2,3†郭建恒1,2‡

(1中国科学院云南天文台 昆明 650011) (2中国科学院天体结构与演化重点实验室 昆明 650011) (3中国科学院大学 北京 100049)

大气逃逸是行星大气演化的重要一环,其主要能量来源为主星在高能波段的辐射.辐射流量随轨道距离的增大会急剧下降,不同轨道处的行星大气逃逸差异较大,轨道距离对系外行星大气逃逸的影响需要深入研究.运用一维流体动力学模型,并且考虑辐射转移和多种粒子的光化学反应过程,对行星大气逃逸随轨道距离的变化进行了研究.由于主星光谱在不同的演化阶段会表现出较大差异,故采用XSPEC(X-Ray Spectral Fitting Package)中的等离子体模型APEC(Astrophysical Plasma Em ission Code),获得不同年龄的类太阳星光谱作为模型输入光谱.结果发现:不同轨道处的行星逃逸率显著不同,逃逸机制也会随轨道距离的增大由剧烈的流体动力学逃逸转化为缓和的金斯逃逸,且行星引力势越小、恒星-行星系统越年轻,这一转化距离越远.处于年轻恒星-行星系统中的短周期行星,逃逸率和辐射流量的相关性降低.这个结果表明经典的能量限制(Energy-lim ited)逃逸理论对这类行星是不适用的.这些发现丰富了对系外行星大气逃逸过程的研究,尤其是扩展了在不同轨道距离和恒星年龄条件下,逃逸机制和能量转换过程的研究.

流体动力学,行星和卫星:大气,恒星:类太阳星,X射线:恒星

1 引言

在主星剧烈的XUV辐射(X-ray and extreme-ultraviolet,1–920˚A)驱动下,许多短周期系外行星大气以及早期的太阳系行星大气都可能经历了快速的流体动力学逃逸过程[1−3].2003年,通过分析由哈勃太空望远镜获取的热木星HD 209458b的凌食数据, Vidal-M ad jar等[1]首次发现了其表面存在蒸发的上层大气,并且正在进行流体动力学逃逸.他们估算出逃逸率大约为1010g/s.此后,Lecavelier Des Etangs等[2]通过对热木星HD 189733b 3次凌食数据的分析,将其逃逸率限制在109–1011g/s.目前只有空间望远镜具备探测此类现象的能力,相较于有限情况的观测研究,理论研究可以扩展到更广泛的恒星-行星系统,得到逃逸率对其他物理参数的依赖情况.对于短周期行星的模型研究发现,由于大气温度极高(可达10000 K[2]),其逸散层底(exobase,大气标高等于粒子碰撞平均自由程处,以上为逸散层)可能位于洛希瓣边界以上,主星潮汐力能使逃逸率显著提高[4].

主星XUV辐射流量是影响行星大气逃逸的最关键因素.行星接收到的辐射流量由主星性质及轨道距离决定.主星性质决定了XUV波段的辐射总光度LXUV.由于主星处于不断的演化之中,恒星光谱能量分布(spectral energy distribution,即SED)也会随之演化.恒星早期磁场活动剧烈,自转速度快,高能辐射非常强,年轻的类太阳星X射线总光度比现在太阳的高3–4个量级[5−6].对于轨道距离为a的行星,其接收到的XUV波段的辐射流量FXUV为:

由此可见,对于同一系统中的行星,其接收到的辐射流量随轨道距离的增加迅速下降.

行星上层大气被来自主星的高能辐射加热后,大气急剧膨胀,进而摆脱行星的引力束缚.经典的能量限制(Energy-lim ited)理论指出,逃逸率和行星接收到的XUV波段的流量成正比[4,7].按照能量限制理论,随着轨道距离的增加,逃逸率会迅速减小.更重要的是,随着轨道距离的增加,当XUV波段的辐射流量下降到不再使行星大气满足流体动力学逃逸条件时,逃逸机制将会由剧烈的流体动力学逃逸转化为缓和的金斯逃逸,逃逸率也剧变到极低值(例如:用金斯逃逸计算,WASP 10b的逃逸率仅为0.6 g/s[8]).

此外,行星大气逃逸也会影响到行星的结构和演化.对于短周期小质量行星,剧烈的流体动力学逃逸过程有可能剥离掉其全部大气,仅遗留岩质内核;而对于大质量行星,大气逃逸影响较小[9].当行星引力势超过1013.6erg/g时,由于加热效率过低,甚至无法进行流体动力学逃逸[8].

恒星XUV辐射加热行星大气的过程非常复杂,尽管此前已有大量关于系外行星大气逃逸的模型研究,但是许多简化为单光子能量模型[10−11],导致许多重要的物理过程被忽略.2007年,Koskinen等[12]研究了类木星大气逃逸机制由流体动力学逃逸向金斯逃逸转化的轨道距离,估算出主星年龄为100 M yr时为1.7 au,年龄为6.7 Gyr时则减小到0.13 au.他们的研究是基于XUV波段总辐射流量做出的推算,没有考虑主星光谱能量分布及其随年龄演化产生的影响.实际上,能量越高的光子其光致电离吸收截面越小(σE∝,E是光子能量)[13],从而能穿透到大气更深层.行星大气的加热主要源自光致电离(离解)产生的光电子,这些光电子会通过碰撞过程将能量转移给更多的粒子,高能光子经历一次光致电离所产生的光电子,能量仍然很高,能进一步产生二次甚至多次电离[14].不同能量光子穿透能力和多次电离能力的不同导致光谱能量分布会影响大气结构和加热过程.由此可见,对大气逃逸的研究,并不能简单地用总辐射流量或单光子能量替代光谱能量分布[15].此外,许多已有模型未考虑X射线的加热作用[3,10−11,16−17].虽然X射线的光致电离截面远小于EUV,但是考虑到恒星早期X射线辐射极其剧烈,此时忽略X射线的影响可能并不合理.

在本文中,我们将基于流体动力学模型,重点研究轨道距离对系外行星大气逃逸的影响.由于行星和主星性质也会影响大气逃逸,在模型研究中我们选取了3颗具有代表性的行星:热木星HD 209458b、热海王星GJ 436b和超级地球Kepler-11b;并使用XSPEC软件包构造了不同年龄阶段类太阳星的XUV光谱,这些光谱包括:刚进入主序(0.1 Gyr),太阳年龄(4.6 Gyr)和主序后期(8.0 Gyr).在本文中,第2部分介绍了本次研究使用的一维流体动力学模型及主星光谱的构造方法.为了使研究更接近物理实际,并且能进一步研究逃逸机制转化和能量转换,模型充分考虑了辐射转移过程和多种光化学机制.第3部分是结果和讨论,对非短周期行星研究了其逃逸机制由流体动力学向金斯逃逸的转化;对短周期行星研究了其在主星辐射能趋于饱和的情况下,能量的转换过程和结果.第4部分是结论与展望.

2 一维大气逃逸模型

本文使用一维行星大气流体动力学逃逸模型[10,16,18],可用于研究径向膨胀的行星上层大气.该模型考虑了电子和H、He两种元素的光化学反应,总计9种粒子:H2、H、He、H+、、、He+、HeH+和电子;输入光谱为太阳的EUV光谱.为了使研究更接近物理实际,本次研究对模型主要做了以下两点扩展:考虑X射线辐射的加热作用,并且从太阳年龄扩展到主序阶段不同年龄;加入重元素C、N、O、Si的光致电离和多种化学反应.所以在本文中,模型总共考虑了18种粒子的光化学反应:7种中性粒子H2, H,He,C,N,O,Si;10种离子H+,,,He+,HeH+,C+,N+,O+,Si+,Si2+和电子.和EUV光子相比,X射线光子光致电离截面小,加热作用不明显,但是光致电离截面随着原子序数的增大而增大(σZ∝Z5,Z是原子序数)[13].因此,在考虑了X射线的情况下,重元素的作用变得更加重要.此外,观测研究也揭示了系外行星大气中存在重元素[19−21],所以包含重元素的光致电离(离解)能更真实地反映X射线的加热作用.

2.1 方程和假设

模型中18种粒子都有对应的粒子数密度nj和连续性方程,下标j表示粒子种类.但是由于粒子耦合,各种粒子的速度和温度都相同[10].模型的下边界为大气热层底部R0,对应的下边界温度为T0.因为R0和行星表面非常接近,计算时可以用行星半径Rp代替R0,行星表面有效温度Teff代替T0.我们设定轨道距离为0.05 au时,下边界温度为1000 K,即T0(a=0.05 au)=1000 K.如果不考虑行星反照率和自转速度的差异,假设行星a的表面温度和轨道距离分别为T1和a1,行星b的表面温度和轨道距离分别为T2和a2,由Parm entier等[22]的研究成果可推导出行星表面有效温度和轨道距离的关系为:

由此可得到模型所需的任意轨道处的下边界温度.模型输入的行星大气元素丰度为太阳丰度[23].由于大部分分子在热层底部已经高温离解[17]且重元素占比极低,在模型中仅考虑占比高的H和He两种元素的分子化学,而重元素部分不考虑分子化学.此外,我们还考虑了模型中18种粒子的以下过程:光致电离(离解)、碰撞电离、复合、电荷交换和其他重要反应.相关反应和反应率[17−18,24]在表1中列出.

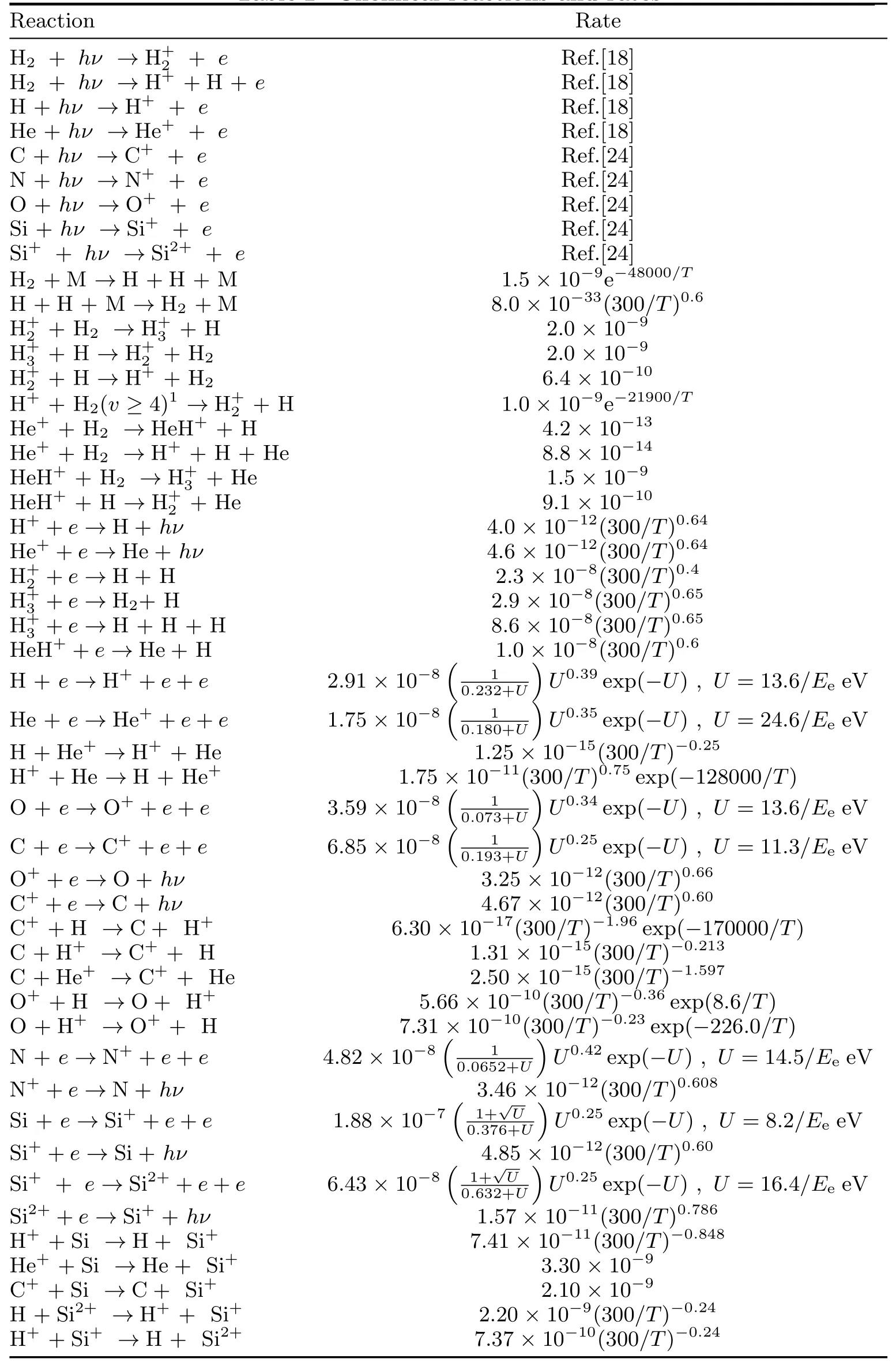
表1 化学反应及速率Tab le 1 Chem ica l reactions and rates

行星大气逃逸的动力学过程用以下多粒子一维流体动力学方程组表示:

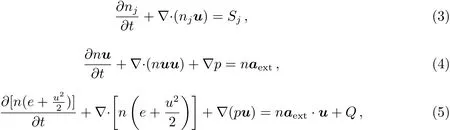
其中,n和u分别表示气体整体的粒子数密度和速度.j表示不同种类的粒子.Sj表示单位时间内,由于光化学反应,某种粒子的产生和湮灭.e=kT/(γ−1)µ是比内能,k是玻尔兹曼常数,T是温度,µ是平均分子量.模型设定γ=5/3.p是压强.aext表示由主星潮汐力、行星引力和公转共同产生的合力.主星质量M∗设定为一个太阳质量.Q=H−L是净加热率,其中H表示主星的辐射加热,L表示行星大气的辐射冷却和化学热.ηj,ν定义为净加热效率,下标ν表示入射光的波长.因此,总加热可表示为:

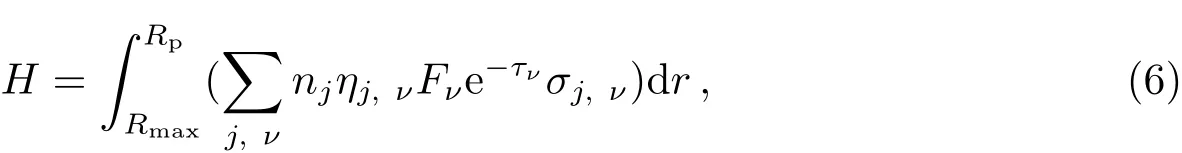
其中Fν和σν分别为辐射流量和光致电离截面.Rmax表示行星大气上边界,模型设定为15Rp.由于高能辐射下的加热过程二次电离非常重要[14],对模型中占比极高的H、He和H2这3种粒子,在计算ηj,ν时考虑了多次电离[18].其他粒子则简化计算: ηj,ν=(hν−Ej)/(hν),其中Ej为粒子电离能,h为普朗克常数.

一维流体动力学模型描述的辐射转移的方向为主星和行星中心的连线.在计算总辐射能量时,考虑到行星背对着主星的一面并没有接收辐射,而正对主星的一面辐射角不同,考虑辐射投影之后等效面积为πr2,相对于行星面积4πr2需乘以1/4因子[4,8].这个1/4因子近似了恒星辐射在行星大气上的有效值,所以在计算逃逸率时,我们乘以1/4因子以修正一维模型:

其中,r为粒子和行星中心的距离,ρ为粒子密度,v为粒子速度.

辐射转移是决定行星大气结构最重要的过程.考虑非潮汐锁定下的一维辐射转移,入射光特定频率的光深为:

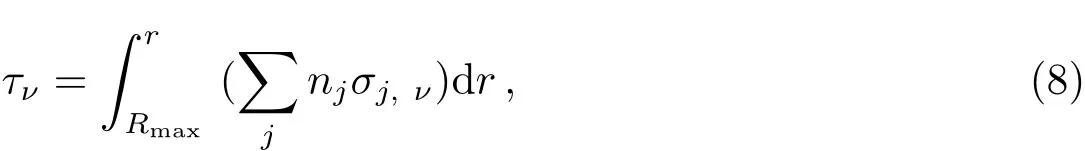
则一个不依赖于频率的平均光深可通过下式给出:

我们将使用这个平均光深来定义行星吸收恒星辐射的特征半径(τ=1的半径处).

2.2 XUV光谱能量分布

行星围绕恒星运转,其大气逃逸由主星XUV波段的辐射主导.随着主星年龄的增长,自转速度变慢,高能辐射减小,光谱曲线软化[5].我们根据Sanz-Forcada等[25]给出的关系式计算恒星X射线和EUV随年龄演化的光度值:

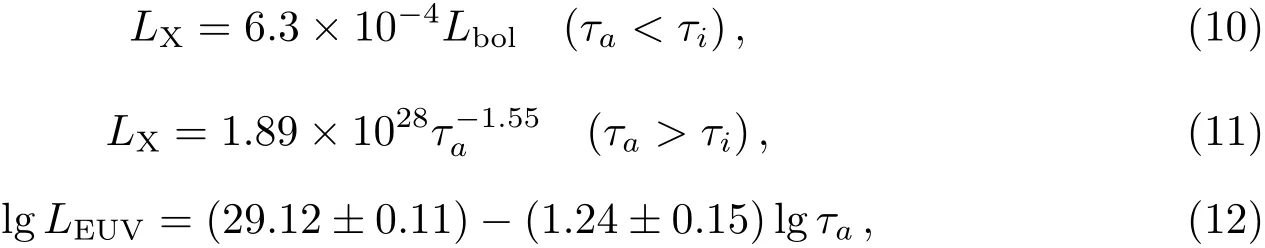
LX由晚期F型星到早期M型星的观测数据给出,Lbol表示恒星总光度,τa表示恒星年龄, τi=2.03×1028L−0.65bol.由于我们研究的是主序星,一般τa>τi.此外,我们计算得出的LX(τa=4.6 Gyr)=1.775×1027erg/s(4.6 Gyr为太阳年龄)和太阳的值相差不大,后者大约为LX=1027erg/s[26];在EUV波段,计算得出LEUV(τa=4.6 Gyr)最小值为1.227×1028erg/s,最大值为3.218×1028erg/s,其中最小值1.227×1028erg/s和太阳的值接近[27].所以我们通过以上关系式可以得到类太阳星X射线和EUV随年龄演化的光度值为:

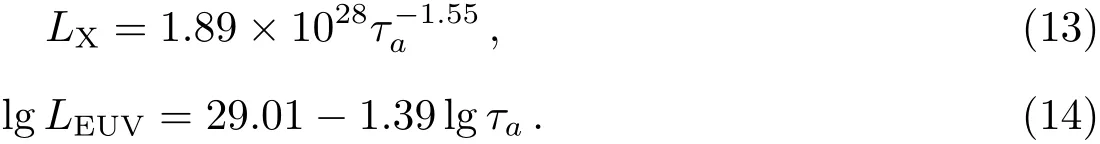
设定恒星年龄为太阳年龄(τa=4.6 Gyr),轨道距离为日地距离(a=1.0 au),通过方程(1)可得出FXUV=4.97 erg·cm−2·s−1,非常接近太阳值(4.64 erg·cm−2·s−1[28]).

虽然得到了光度随年龄的演化关系,但是观测上并不能给出特定恒星随年龄演化的光谱能量分布.为了解决这个问题,我们采用Xspec V 12.8.2[29]构造光谱.我们选取XSPEC中的等离子体模型APEC,自由参量为恒星大气金属丰度和冕层温度.我们首先限定金属丰度取太阳丰度[23],这样一来,输出的光谱能量分布只和温度相关.在高能天体物理中,温度通常决定了天体的光谱能量分布.为了得到随年龄演化的XUV光谱能量分布,我们首先在APEC中设定了一系列的冕层温度,然后计算所得光谱的LX/LEUV.由方程(13)和(14)我们可以得到该比值随年龄的演化.所以一旦给定主星年龄,APEC中应设定的冕层温度就可以由这一比值确定.最终,我们可以得到任意年龄的LX、LEUV、LX/LEUV、冕层温度和光谱能量分布.实际上,LX/LEUV提供了隐含在光谱能量分布中的硬度比信息,我们可以把这一比值看做某种色指数.图1比较了主星年龄分别为0.1 Gyr、4.6 Gyr和8.0 Gyr时的光谱能量分布,由图明显可见,主星XUV辐射流量随着演化减小,且在演化早期下降更明显.

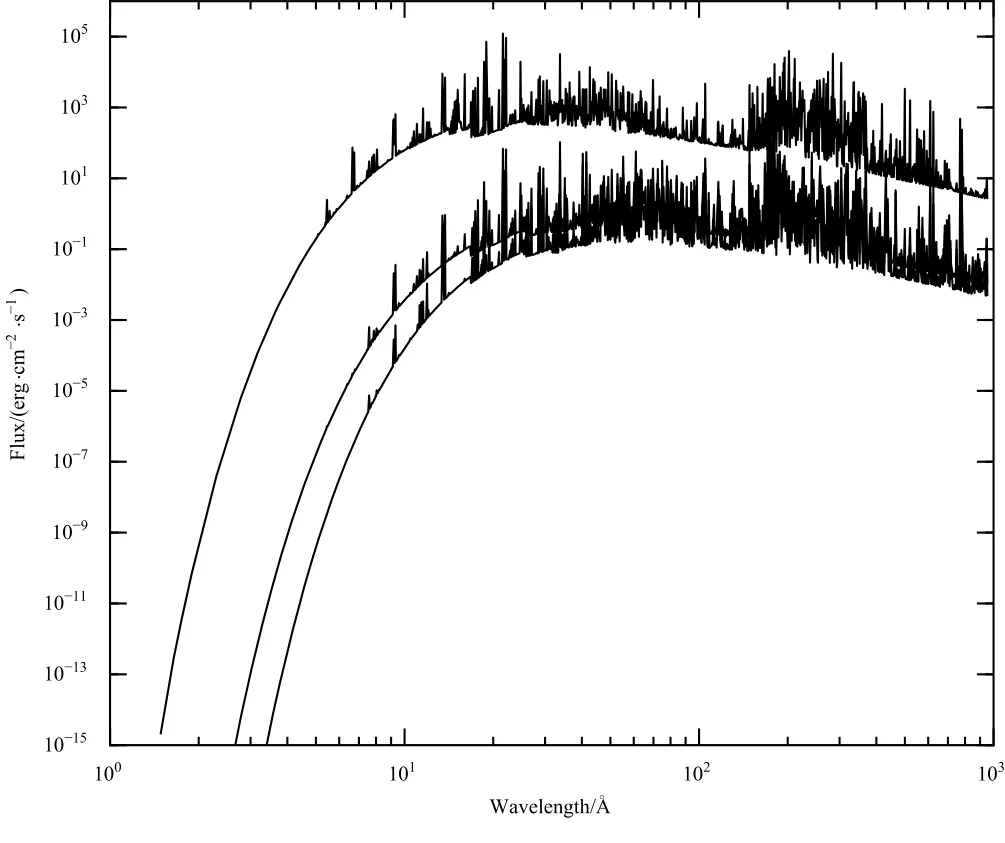
图1 不同年龄类太阳星XUV光谱能量分布.从上往下依次代表0.1 Gy r,4.6 Gy r和8.0 G y r,流量定标在0.05 au.Fig.1 The XUV SED of solar-type stars at d ifferent ages.From top to dow n,the th ree lines rep resent the SED of stars at 0.1 Gy r,4.6 Gy r,and 8.0 G y r,respectively.The flux is ca lib rated with a d istance of 0.05 au.

3 结果与讨论

3.1 逃逸机制

对于那些离主星很近的行星,在主星剧烈的高能辐射驱动下,行星上层大气温度可高达10000 K[2].在高压的推动下,气体急剧膨胀并形成迅速逃逸的气体流,即为流体动力学逃逸.对于那些离主星较远的行星,其大气动力学过程较为缓和.热运动着的、仅作弹性碰撞的粒子,其速度分布服从麦克斯韦分布.只有那些速度足够快的粒子(在麦克斯韦分布的高能尾巴附近)有足够的动能摆脱行星的引力束缚向行星际空间逃逸,这种逃逸机制则为金斯逃逸,单位面积的逃逸率ϕesc(单位particles·m−2·s−1)可由金斯定则给出:

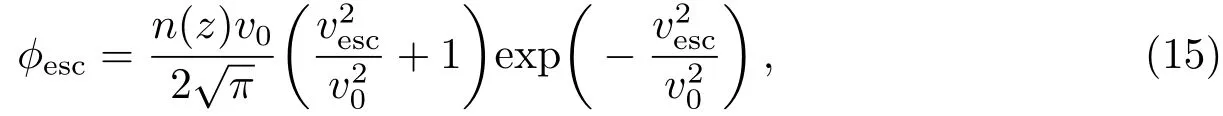
上式中,n(z)为粒子数密度,vesc为逃逸速率,v0为最可几速率.金斯逃逸非常缓和,比如:用金斯逃逸估算,WASP-10b的逃逸率仅为0.6 g/s[8];而流体动力学逃逸则非常剧烈,模型给出的逃逸率通常能达到1010g/s,会对行星演化产生更快速、更显著的影响(尤其对小质量行星).另一方面,在金斯逃逸中,只有达到逃逸速率的粒子能够摆脱行星的引力束缚从而逃逸出去,重元素更难达到逃逸速率,所以金斯逃逸对轻元素有显著的偏向性,目前的地球可能就是轻元素通过这种方式逃逸出去而重元素会留下来[30];而流体动力学逃逸是一种很强的热逃逸机制,重元素在和轻元素频繁碰撞后会随之逃逸[30].两种逃逸机制产生的演化结果可能差异巨大,所以在研究行星大气逃逸时,必须对逃逸机制做出判断,否则对演化的研究误差将极大.流体动力学逃逸由主星剧烈的高能辐射驱动,从方程(1)可知行星大气接收到的辐射流量和轨道距离的二次方成反比,当辐射流量下降到使行星大气不能满足流体动力学逃逸条件时,逃逸机制将会由流体动力学逃逸转化为金斯逃逸.

此前的研究[12,15]一般使用经典的金斯边界条件[12]判断逃逸机制.该条件指出,若粒子在大气逸散层底rexo的平均动能3kT/2不小于此处行星引力势能GMpm/rexo,即热逃逸参数χ满足χ=GMpm/(kT rexo)≤1.5,则为流体动力学逃逸.值得注意的是,在计算引力势能时,金斯边界条件并未考虑主星潮汐力,但是潮汐力实际上会减小行星对粒子的引力束缚;甚至对于某些短周期行星,尽管不满足金斯边界条件,但是由于逸散层底位于洛希瓣边界上方,实际上在逸散层的粒子已不受行星引力束缚[4].逃逸机制的转化是一个复杂的过程,和大气组成等也有关系,简单地将χ=GMpm/(kT rexo)≤1.5用于判断所有情况并不合理.Volkov等[31]对不同成分的大气直接使用蒙特卡洛模拟来研究逃逸机制的转化条件,发现χ∼2–3.6.因此,在我们的研究中考虑了洛希瓣效应,首先使用Koskinen等[12]的方法判断逸散层底(逸散层底的压强大约为3.7 pbar),然后采用Volkov等[31]的判据(χ∼3)来估算逃逸机制发生转化的轨道距离.考虑洛希瓣效应后,引力束缚∆Φ为[4]:

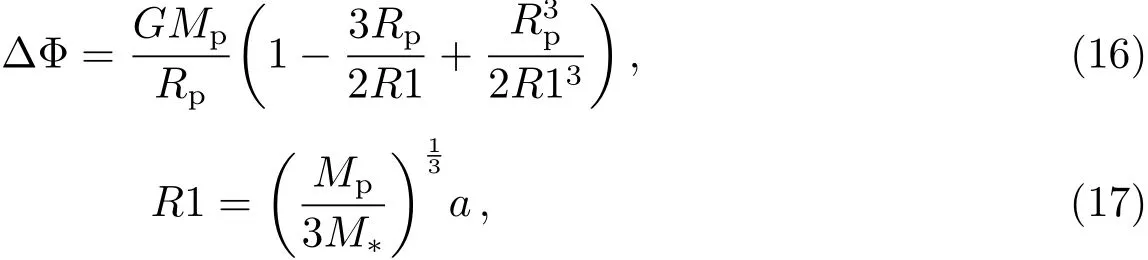
其中,G为引力常数,R1是洛希瓣边界,∆Φ为行星表面和洛希瓣边界的引力势之差,在方程(16)中用粒子所在半径代替行星半径Rp,则可得出粒子需要克服的引力势.

为了更全面地研究逃逸机制转化时的轨道距离,我们选取了3颗不同质量和半径的行星:热木星HD 209458b、热海王星GJ 436b和超级地球Kepler-11b,3颗行星的参数见表2.我们首先严格按照表2中的参数对模型进行了试算,物质损失率为:Kepler-11b, 5.6×108g/s;GJ 436b,1.2×1010g/s;HD 209458b,6.9×1010g/s.此前的研究中已有大量关于HD 209458b逃逸率的计算,量级为1010g/s[16−17,32],其中Garc´ıa M u˜noz在2007年给出的逃逸率为6.1×1010g/s[32],我们的结果非常接近这一值.我们进一步分别研究这3颗行星在主星年龄为0.1 Gyr、4.6 Gyr和8.0 Gyr时不同轨道距离处的大气逃逸,分别代表主序阶段年轻、壮年和年老的情况.不同年龄的入射光谱见图1.

表2 行星参数Tab le 2 P lanetary param eters

我们的计算结果显示在图21研究重点为非短周期行星流体动力学逃逸向金斯逃逸的转化,为了呈现完整的趋势及进一步分析短周期行星在辐射能量趋于饱和时的能量转换情况,将杨沫和郭建恒之前工作中已得出的短周期行星的逃逸率包含在图中.,星号表示流体动力学逃逸向金斯逃逸转化的轨道距离.需要注意的是,我们的模型使用了流体的假设,这个假设并不适用于那些粒子之间耦合不紧密的气体团,即不能用来求解金斯逃逸.因此,在星号之后的物质损失率应该使用玻尔兹曼方程求解,对于确定为金斯逃逸的区域可以使用金斯定则(方程(15)),本文的结果可能比实际情况偏大数个量级.但是,对星号以前的部分,我们的结果明确地说明了它们存在着流体动力学逃逸,并给出了逃逸率.这个临界点(星号)明确表示了在某个轨道距离处,流体动力学逃逸将向金斯逃逸转化.对于金斯逃逸的计算(星号之后的部分),超过了本文的范围,我们希望以后进行进一步研究.总而言之,用不适合的逃逸机制进行计算,可能会造成极大偏差,所以在研究大气逃逸时确定逃逸机制非常重要.

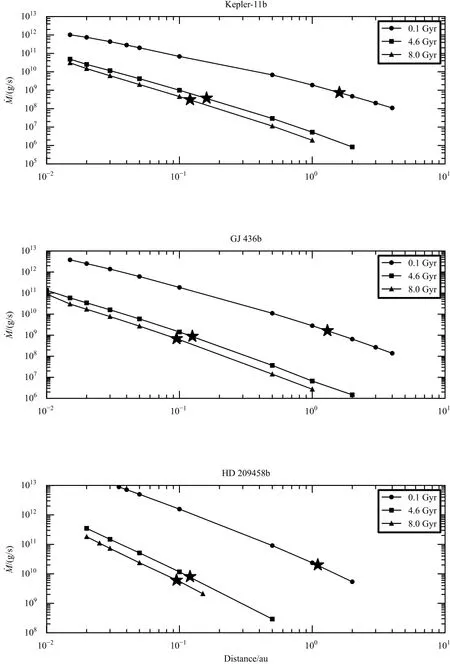
图2 不同轨道距离处的逃逸率.星号代表临界点.Fig.2 The m ass loss rates at d ifferen t orb ita l d istances.C ritical poin ts are show ed by stars.

由图2可见,HD 209458b能够进行流体动力学逃逸的轨道距离远小于Kepler-11b.实际上在模型计算过程当中,我们无法模拟更远轨道距离处HD 209458b的大气逃逸.随着轨道距离的增加,HD 209458b接收到的辐射流量迅速下降,而且对模拟数据的分析发现,几乎全部的辐射能都通过行星大气的红外辐射冷却过程散失,并没有用于推动大气逃逸,这和Salz等[8]对大质量行星加热效率的研究结果一致.总体上,逃逸率随着轨道距离和主星年龄的增加而下降,变化区间大约为1013g/s到108g/s(星号前).但是,由于入射光谱区别不大(见图1),4.6 Gyr和8.0 Gyr的逃逸率相差并不显著.另外,逃逸机制发生转化的轨道距离,也依赖于主星年龄和行星本身的性质.主星年龄较年轻和行星引力势较小的情况下,流体动力学逃逸能在更远的轨道距离处进行.这是因为年轻恒星能提供更多的高能辐射,使行星大气粒子有更高的动能;而行星引力势小意味着更容易摆脱引力束缚,从而χ值更小.在0.1 Gyr时,3颗行星能进行流体动力学逃逸的轨道距离都超过了1 au.但是在8.0 Gyr时,HD 209458b仅能在小于0.095 au的轨道距离内进行流体动力学逃逸.在4.6 Gyr时,转化距离在0.1–0.2 au,这和Koskinen等[12]的研究结果一致.

在0.1 Gyr时,Kep ler-11b的转化距离为1.6 au.在我们太阳系中,水星、金星、地球和火星的质量和引力势都远小于Kep ler-11b且公转轨道距离小于1.6 au,这意味着这些行星在早期演化中都经历过快速的流体动力学逃逸过程.我们将太阳年龄设定为0.1 Gyr,对火星(轨道距离为1.5 au)的大气逃逸过程进行了模拟.结果发现其满足流体动力学逃逸条件,逃逸率为0.65×109g/s.

3.2 逃逸率

首先介绍经典的能量限制理论.如果用Q表示行星单位时间获得的净能量,q表示粒子单位质量的能量,逃逸率可用=Q/q表示.净能量Q来源于主星辐射(主要)和其他来源,例如行星引力波和内能,并且通过化学反应和红外辐射等过程损失一部分能量.对于能够逃逸到行星际空间的粒子,它们必须摆脱行星的引力束缚,所以q包含了引力势能∆ϕ、动能v2R1/2和热能cpTR1.如果假设全部的能量都用来帮助逃逸粒子摆脱引力束缚,则粒子能量q简化为引力势能;且不考虑除主星辐射外的能量来源,可推导出估算逃逸率的能量限制方程[4,7]:

我们模型的逃逸率由方程(7)给出.因为模型包含了辐射转移、辐射冷却和光化学等微观物理过程,所以可以直接得到β和η的值.将β和η代入方程(18),可以修正能量限制情况下的逃逸率.我们在图3列出了不同情况下恒星辐射在行星大气中的吸收.图中主星辐射较强的3条线(上面的3条线)分别表示主星年龄为4.6 Gyr、轨道距离为0.02 au时3颗行星对辐射的吸收,而辐射较弱的线(最下面的线)是主星年龄为8.0 Gyr、轨道距离为0.1 au时Kepler-11b的吸收情况.由图可见,主星辐射在大气上层吸收极少,在下层迅速减小,这是因为在引力束缚下大气粒子密度随半径增加,近似呈指数衰减;对小质量行星,引力势往往较小,所以其对粒子的引力束缚相对较弱,粒子密度衰减慢,相对大质量行星,其上层大气中有更多粒子吸收主星辐射,β值明显更大.对所有数据分析发现:大部分情况下,β的取值非常接近1(∼1.1),即主星辐射几乎能穿透到大气底层,估算逃逸率时假定β因子为1并不会带来明显误差(大部分估算都假定β因子为1).但是小质量行星在遭受强主星辐射时大气剧烈膨胀,β因子超过1.5,即特征吸收半径大约是行星半径的1.5倍.在这种情况下,确定合理的β值,则变得很重要.通过分析数据还发现,相较于β取值的小幅波动,η变化范围极大.一般η∼0.1–0.5,但是对大质量行星,在辐射流量较小时η可降至0.01以下,进一步降低辐射流量将无法进行流体动力学逃逸.这主要是因为大质量行星的引力势能大,如果能逃逸则意味着温度足够高以产生足够的压力梯度,而高温会大大促进辐射冷却,从而降低加热效率[8,18].

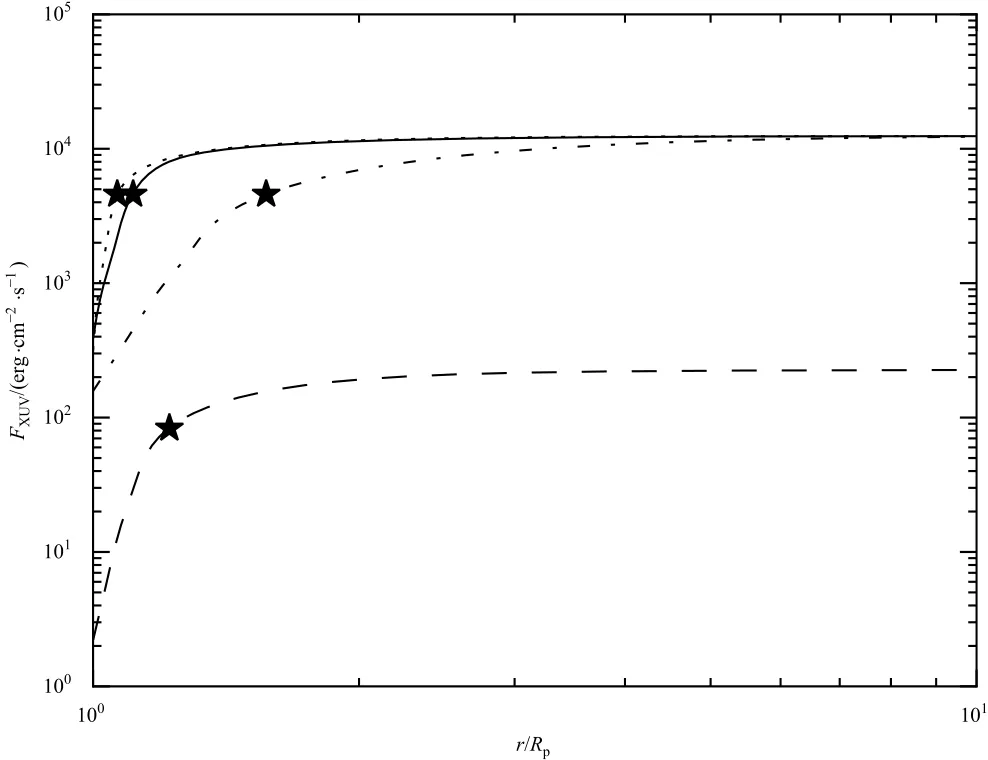
图3 主星辐射在行星大气中的吸收.上面的3条线代表主星年龄为4.6 Gy r,轨道距离为0.02 au,其中点线为HD 209458b,实线为G J 436b,点虚线为K ep ler-11b.下面的虚线代表K ep ler-11b,参数为8.0 G y r、0.1 au.星号标示了光深为1处.Fig.3 Absorp tion of stellar rad iation in p lanetary atm osphere.The dotted,so lid,and dot-dashed lines rep resen t the resu lts of HD 209458b,G J 436b,and K ep ler-11b,respectively,and the stellar age is 4.6 Gy r,the orb ita l d istance is 0.02 au.T he dashed line show s the resu lt of K ep ler-11b with a stellar age of 8.0 G y r and an orb ital d istance of 0.1 au.Stars denoteτ=1.

图4为对行星大气流体动力学逃逸,模型和能量限制方程所得逃逸率的比较,能量限制方程中β和η的取值由模型给出.由图可见,越年轻、轨道距离越近、行星引力势越小,模型和能量限制理论偏差越大.主星年龄为0.1 Gyr、轨道距离为0.015 au时,对Kep ler-11b两者能相差近两个数量级.越年轻、轨道距离越近意味着辐射流量越大,此时行星大气被剧烈加热,除了引起快速流体动力学逃逸,逃逸粒子也获得了极高的动能和热能,但是能量限制理论忽视了动能和热能带走的能量,导致结果严重偏高.而行星引力势越小,意味着粒子需要克服的引力势能在总能量中的占比越小,动能和热能占比越高,这种情况下忽略了动能和热能的能量限制理论误差会更大.图中,接收辐射流量较小的行星(轨道距离大、主星年老),模型和方程(18)结果较一致.值得注意的是,理论上能量限制方程计算的为逃逸率上限,但是有时模型结果会略大于此“上限”,这是由于方程(18)忽视了除主星辐射之外的能量来源,而模型在给出边界条件时已经设定了行星大气下边界的温度,相当于能量来源还有行星内能.

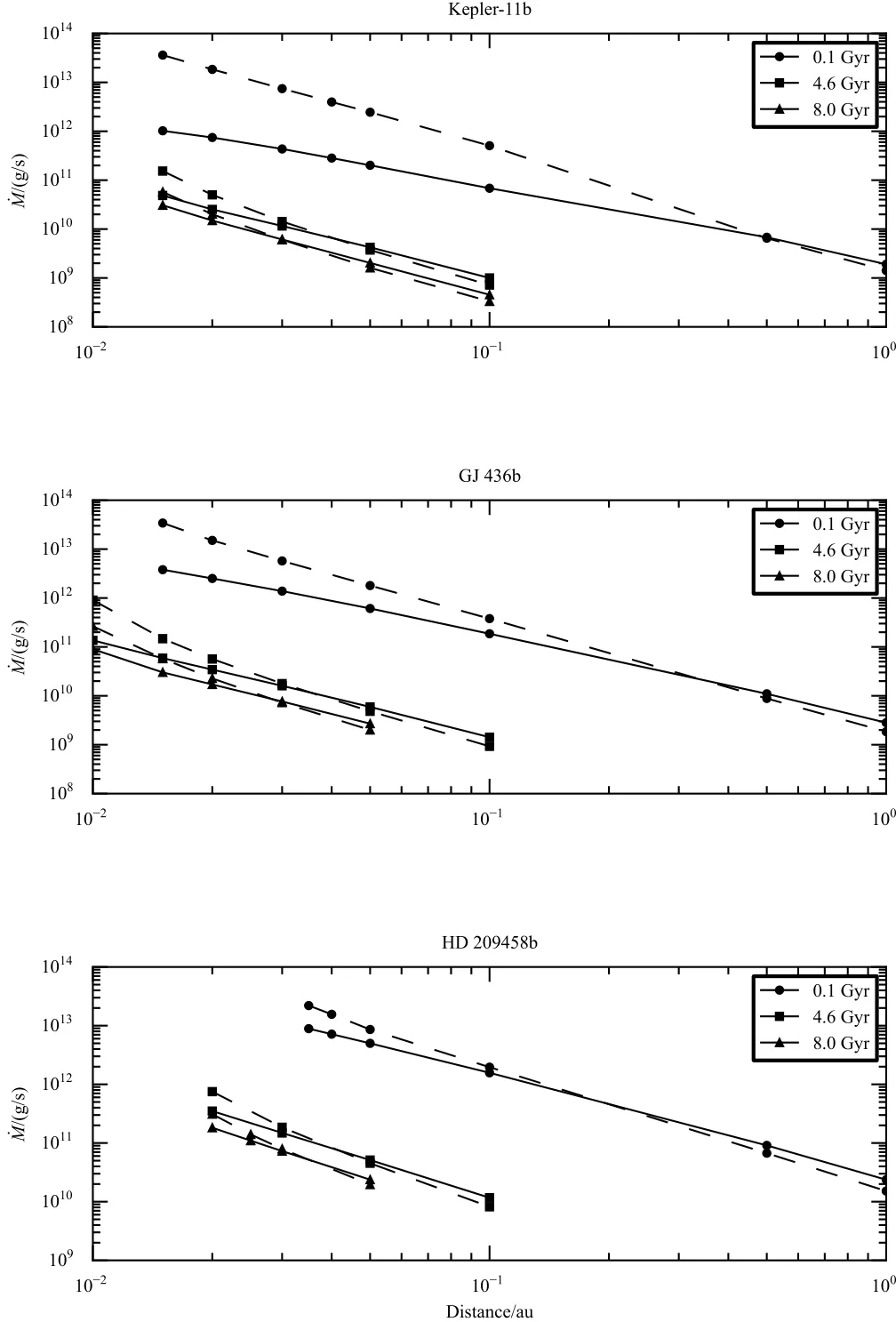
图4 模型和能量限制理论的比较.实线为模型结果,虚线为能量限制方程计算结果.Fig.4 Com parison betw een ou r m odel and the energy-lim ited equation.T he solid lines rep resent the resu lts of ou r m odel,w h ile the dashed lines stand for the energy-lim ited equation.

除了定性分析,由模型得出行星大气的温度和速度结构后(见图5),可定量给出能量转化的结果.在洛希瓣边界高度,单位质量粒子增加的热能和动能分别为:

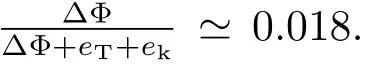
4 总结与展望

本文讨论了轨道距离、主星年龄、行星性质对行星大气逃逸的影响,尤其是轨道距离对逃逸机制和能量转换过程的影响.我们发现不同轨道处的行星逃逸率显著不同,逃逸机制也会随轨道距离的增大由剧烈的流体动力学逃逸转化为缓和的金斯逃逸,且行星引力势越小、恒星-行星系统越年轻,这一转化距离越远.在0.1 Gyr时,流体动力学逃逸在超过1 au处仍能进行,意味着在太阳系早期,水星、金星、地球和火星都经历了快速流体动力学逃逸阶段.而对于处于年轻恒星-行星系统中的短周期、小引力势行星,逃逸率和轨道距离及辐射流量的相关性降低,大部分能量转化为粒子热能和动能,和经典的估算逃逸率的能量限制理论能相差近两个数量级.实际上,除了能量限制的情况,还存在多种模式的大气逃逸[35],对这些模式我们还需更细致的研究;此外,虽然本文的工作包含了主星年龄为0.1 Gyr、4.6 Gyr和8.0 Gyr时的大气逃逸,分别代表主序阶段年轻、壮年和年老的情况,但是大气逃逸会影响行星演化和分布情况[36−38],我们将在今后的工作覆盖更多的主星年龄,以进一步研究大气逃逸对演化的影响.

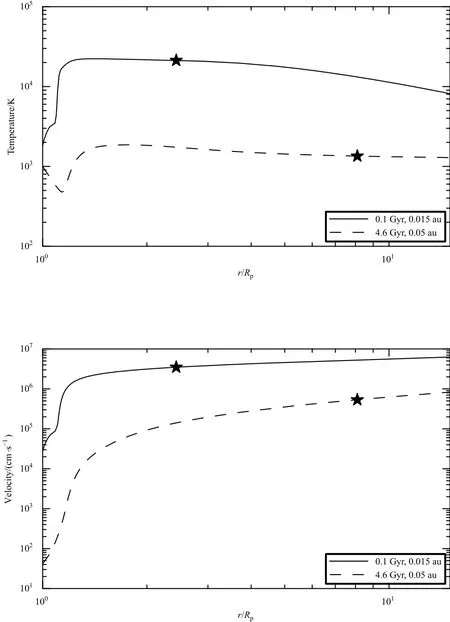
图5 Kep ler-11b大气温度和速度结构.上方的图为温度结构,下方的为速度结构.星号标示洛希瓣边界.Fig.5 Tem p eratu re and velocity structu res of K ep ler-11b.The upper and the low er panels rep resen t the structu res of atm ospheric tem peratu re and velocity,resp ectively.Stars denote the Roche-lobe boundary.

我们的模型已经包括了真实的辐射转移和多种光化学反应过程,能够得出粒子密度分布、温度和速度结构等多个物理量.一维模型反映了恒星-行星中心连线大气的物理特性.在不考虑恒星非球对称引力以及非潮汐锁定的条件下,可以较好地代表行星大气逃逸的物理特性.在使用多维模型的情况下,行星逃逸大气的密度、速度和温度等分布从赤道到极区的情况较为复杂,在这种情况下,不利于得到流体动力学逃逸向金斯逃逸转化的临界点,这是本文使用一维模型的出发点.此外,一维模型具有计算稳定、收敛快、物理结果直观等优势,为我们工作的开展带来了极大的便利,但是一维模型无可避免地会忽视一些物理过程,其中最重要的是在潮汐锁定的情况下,恒星辐射在行星大气水平方向的能量传递.我们的一维模型结果明确反映了恒星-行星中心连线的物理特性,也使用了1/4因子对逃逸率做了修正.尽管这个1/4的因子并不能完全反映多维的情况,但是对于逃逸率的修正是可以接受的[4,8].此外,一维模型还会忽视三维磁场对大气逃逸的影响.大气逃逸是非常复杂的过程,在物理细节上我们仍有许多改进空间,例如粒子沉积过程和大气底层的分子化学.在未来的工作中,我们将进一步完善模型,使模型更接近物理实际.

[1]V ida l-M ad jar A,Lecavelier Des E tangs A,D´esert J M,et a l.Natu re,2003,422:143

[2]Lecavelier Des E tangs A,Eh ren reich D,V ida l-M ad jar A,et al.A&A,2010,514:A 72

[3]T ian F,Toon O B,Pav lov A A,et a l.Science,2005,308:1014

[4]E rkaev N V,K u likov Y N,Lamm er H,et a l.A&A,2007,472:329

[5]Feigelson E D,Gaffney J A III,Garm ire G,et al.Ap J,2003,584:911

[6]Favata F,M icela G.SSRv,2003,108:577

[7]Lamm er H,Selsis F,R ibas I,et al.A p JL,2003,598:L 121

[8]Sa lz M,Schneider P C,Czesla S,et al.A&A,2016,585:L 2

[9]Lecavelier Des E tangs A,V ida l-M ad jar A,M cConnell J C,et a l.A&A,2004,418:L 1

[10]Guo J H.A p J,2011,733:98

[11]M u rray-C lay R A,Ch iang E I,M u rray N.A p J,2009,693:23

[12]K osk inen T T,A y lw ard A D,M iller S.Natu re,2007,450:845

[13]P fefferm ann E.P roportional Coun ters//T r¨um p er J E,Hasinger G.T he Universe in X-Rays.Berlin: Sp ringer,2008:6-7

[14]Cecchi-Pestellin i C,C iaravella A,M icela G.A&A,2006,458:L 13

[15]Chadney J M,G a land M,Un ruh Y C,et al.Icar,2015,250:357

[16]Guo J H.A p J,2013,766:102

[17]Yelle R V.Icar,2004,170:167

[18]Guo J H,Ben-Ja ffel L.A p J,2016,818:107

[19]V idal-M ad jar A,D´esert J M,Lecavelier Des E tangs A,et al.Ap JL,2004,604:L69

[20]V idal-M ad jar A,Hu itson C M,Bou rrier V,et al.A&A,2013,560:A 54

[21]Sw ain M R,T inetti G,Vasish t G,et al.A p J,2009,704:1616

[22]Parm entier V,Gu illot T,Fortney J J,et a l.A&A,2015,574:A 35

[23]A sp lund M,G revesse N,Sauva l A J,et a l.ARA&A,2009,47:481

[24]K osk inen T T,Harris M J,Yelle R V,et a l.Icar,2013,226:1678

[25]Sanz-Forcada J,M icela G,R ibas I,et a l.A&A,2011,532:A 6

[26]Lalitha S,Poppenhaeger K,Singh K P,et a l.A p J,2014,790:L 11

[27]R ichards P G,Fennelly J A,Torr D G.JGRA,1994,99:8981

[28]R ibas I,G u inan E F,G¨udel M,et a l.A p J,2005,622:680

[29]A rnaud K A.adass,1996,101:17

[30]Patrick I.G iant P lanets of Ou r Solar System:An Introduction.Berlin:Sp ringer,2006:56-58

[31]Volkov A N,Johnson R E,Tucker O J,et al.Ap JL,2011,729:L24

[32]Garc´ıa M u˜noz A G.P&SS,2007,55:1426

[33]Lop ez E D,Fortney J J.A p J,2014,792:1

[34]W ang J,Ford E B.M NRAS,2011,418:1822

[35]Ow en J E,A lvarez M A.A p J,2015,816:34

[36]How e A R,Bu rrow s A.A p J,2015,808:150

[37]Jin S,M ordasin i C,Parm entier V,et al.A p J,2014,795:65

[38]Guo J H.A p J,2010,712:1107

The Im pacts of O rbital D istance on Exop lanetary A tm ospheric Escape

YANG Mo1,2,3GUO Jian-heng1,2

(1 Yunnan A stronom ica l Observatory,Chinese A cadem y of Sciences,K unm ing 650011) (2 K ey Labo rato ry fo r the Struc tu re an d Evo lu tion of Celestia l O bjec ts,Chinese A cadem y of Scien ces, K unm ing 650011) (3 Un iversity of Chinese A cadem y of Scien ces,Beijing 100049)

D riven by the high energy radiation of host stars,atmospheric escape is very im portant for planet evolution.W hile the flux drops dramatically with the increase of orbital distance,it is essential to study the im pacts of orbital distance on atmospheric escape.We consider the hydrodynam ic escape of exoplanets driven by the XUV(X-ray and extreme-ultraviolet)radiation of their host stars.We aim to study themass-loss rate,the transition of escapemechanism,the structures of tem perature and velocity,based on a one-dimensionalhydrodynam icmodelwhich includes radiative transfer processesand photochem ical reactions.As the stellar XUV em ission varieswith the stellar evolution,we use XSPEC(X-Ray Spectral Fitting Package)to construct the XUV spectra of solar-type stars at different ages.We find that with the increase of orbital distance,themass-loss rates drop significantly,and when the stellar XUV flux is too small to preserve the hydrodynam ic escape,it w ill turn to Jeans escape.This transition occurs in larger distance for younger and smaller planets.For young p lanets, hydrodynam ic escape can occur in 1–2 au.For very young and close-in planets,the relation between mass-loss rate and stellar flux is not as significant as planets that are not close to their host stars,and the energy-lim ited equation can lead to large overestimate.

hydrodynam ics,p lanets and satellites:atmospheres,stars:solar-type, X-rays:stars

P185;

A

10.15940/j.cnki.0001-5245.2016.06.004

2016-04-08收到原稿,2016-05-04收到修改稿

∗国家自然科学基金项目(11273054)资助

†yangmo215@ynao.ac.cn

‡guojh@ynao.ac.cn