热木星属性对相曲线相位的影响分析∗

田蕾 季江徽

(1中国科学院紫金山天文台 南京 210008) (2中国科学院大学 北京 100049) (3中国科学院行星科学重点实验室 南京 210008)

热木星属性对相曲线相位的影响分析∗

田蕾1,2†季江徽1,3‡

(1中国科学院紫金山天文台 南京 210008) (2中国科学院大学 北京 100049) (3中国科学院行星科学重点实验室 南京 210008)

利用浅水模型研究热木星属性参数对其大气环流平衡图案及相曲线相位的影响,分别考虑了热木星半径、自转速率、表面重力加速度这3个参数变化产生的影响.应用热木星HD 189733b的属性参数进行模拟,结果显示:半径、表面重力加速度变化对于热木星大气环流平衡图案及红外相曲线相位的影响也可以忽略.但自转速率变化对于热木星大气环流平衡图案以及红外相曲线相位的影响较大.进而可以推测,在热木星红外相曲线的长期观测中,若极大值和极小值的相位发生了明显变化,则热木星的自转速率改变有可能是原因之一.

天体力学,流体力学,行星和卫星:大气,方法:数值

1 引言

目前已有超过2000颗系外行星被确认发现(参见网址http:www.exop lanet.eu),其中有一类系外行星被称为热木星.热木星是一类距离中心恒星小于0.1 au、周期在几个地球日之内的气态巨行星.热木星的动力学状态与太阳系内的木星相比,存在两点重要的差异.首先,由于热木星离中心恒星非常近,受到潮汐锁定作用[1−4],可以将其视为同步自转(即自转周期与公转周期相同,方向一致).这就意味着目前发现的大部分热木星周期约为1–5个地球日,是木星自转速率的1/12–1/2,因此对于一定速度的大气流,在热木星上所受的科氏力比在木星上小得多.其次,热木星受到主星的辐射非常强烈,约是木星所受辐射的103–105倍[5].因此,即使在风速很大的情况下,热木星也可能昼夜面温差很大.

近十年,关于热木星的大气环流研究取得了巨大进展.由Spitzer空间望远镜和Hubble空间望远镜观测到的红外光度曲线、光谱为许多热木星的3维温度结构提供了诸多限制条件,暗示了这些热木星上存在着活跃的大气环流运动[6−12].

如图1所示,当系外行星绕着轨道运行,地球上观测到它的辐射通量随其轨道相位的变化而变化,由此可获得相光度曲线,简称相曲线(phase curve)[14].在光学和紫外波段观测获得的相曲线反映的是系外行星的反射光,是关于轨道相位的函数;在近红外和中红外波段观测获得的相曲线反映的是行星的热辐射,直接取决于系外行星的温度、大气成分以及随经度的变化.红外相曲线反映了系外行星的昼夜面差异,可用于探测系外行星大气运动[15−19].不同的大气环流结构在红外相曲线上有着不同的反映.如果行星同步自转且无赤道风,则最热区域位于星下点位置,相曲线与轨道的相位一致,亮度最大值出现在凌星次掩(secondary eclipse).但是如果行星上存在大气环流,则会导致行星上的热分布改变,最热区域偏离星下点,如图2所示,红外相曲线峰值的相位就会偏离凌星次掩[20−24].

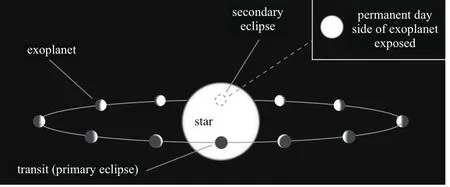
图1 系外行星绕着轨道运行示意图.地球上观测到系外行星辐射通量随其轨道相位的变化而变化,由此可获得相光度曲线[13].Fig.1 A d iagram of an exop lanet’s m otion in a circu lar orbit.Phase cu rves can be ob tained accord ing to the variation of rad iative flux[13].

目前已有很多基于同步自转圆轨道短周期的3维热木星大气环流模型,但是大气3维环流模型包含很多复杂的相互作用过程,往往导致难以分辨何种动力学机制占主导地位[21,25−36].因此,简化的模型在研究巨行星的大气动力学中起到了非常重要的作用[37−40].尤其是在研究行星尺度的大气环流运动时,可以忽略垂直方向上的运动过程,而简化为2维模型.浅水模型(shallow-watermodel)是描述行星大气运动的2维模型中形式最简单的,在研究行星的大气和海洋的运动方面有着广泛应用.对于自转较快的气态巨行星,由Taylor-Proudman定理可知,在流体静力学平衡状态下(科氏力与压力平衡),行星速度场呈现2维分布,只有垂直于自转轴的水平方向速度,也即沿经度方向运动的地转流(geostrophic flow).对于不同的纬度,运动方向可能相反,形成方向交替的带状流,这是自转气态巨行星大气环流的基本特征.

浅水模型是对球面局部平面化,模型中赤道上的科氏项为0,而在地转流近似中科氏项最大,虽然这样的近似处理对于赤道附近带来的误差较大,但对中纬度以及大尺度的全球环流模拟比较实用.

Showman等人利用浅水模型研究了阻力时标和辐射时标对于潮汐锁定的系外行星大气环流的影响[39].Perezbecker等人基于浅水模型研究了热木星昼夜温差程度对大气环流的影响[41].Showman等人基于3维模型研究了热木星的轨道距离和自转速率对于大气环流的影响[42].Kaspi等人利用3维模型研究了系外类地行星包括半径、自转速率、行星平均密度等属性对于大气环流的影响[43].

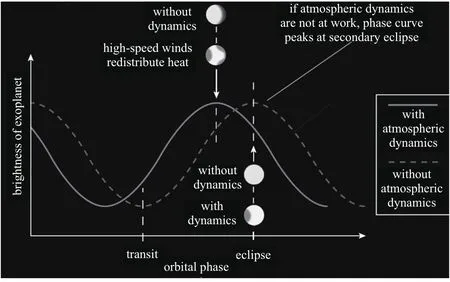
图2 系外行星的红外相光度曲线.它表示辐射通量随轨道相位变化,系外行星上若存在大气环流运动,辐射通量的峰值可能会出现在凌星次掩之前[13].Fig.2 In frared(IR)phase cu rves of exop lanets.In frared phase cu rves exh ib it flux variations with orb ital phase.If atm ospheric dynam ics are at w ork,a flux peak m ay occu r before secondary eclipse[13].

本文通过对STSWM(Spectral Transform Shallow Water Model)程序包进行修改,利用浅水模型来研究热木星自身属性参数对其大气环流平衡图案及相曲线相位的影响,分别考虑了热木星半径、自转速率、表面重力加速度这3个参数变化产生的影响.本文第2部分介绍浅水模型如何应用于热木星大气环流的模拟;第3部分介绍求解该模型的算法;第4部分分别展示热木星半径、自转速率、表面重力加速度对大气环流平衡图案的影响,以及对其相曲线相位的影响;最后一部分进行总结与讨论.

2 模型

2.1 浅水方程

浅水方程以有限的自由面高度描述不可压缩流在重力和科氏力作用下随时间的演化[44],从而为模拟行星尺度的大气运动提供了简便途径.浅水方程包括动量方程和质量连续性方程.

若不考虑摩擦,动量方程写作:

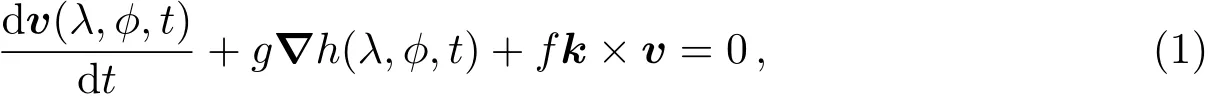
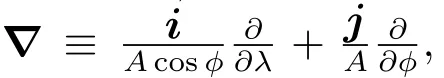
2.2 应用于热木星大气

基于浅水模型,我们拟研究热木星的大气运动.基于Showm an等人建立的热木星大气浅水模型[39],需要在浅水方程的基本形式上做一些修改,结合热木星的情况,突出同步自转、昼夜面温差大等特征.Showman采用一种理想的两层浅水模型来模拟热木星大气的热量传输.如图3所示,假设模型的上层密度ρupper较小,代表行星大气中气象活动活跃的大气层.下层无限深,密度ρlower比上层密度大,代表巨行星的内部.

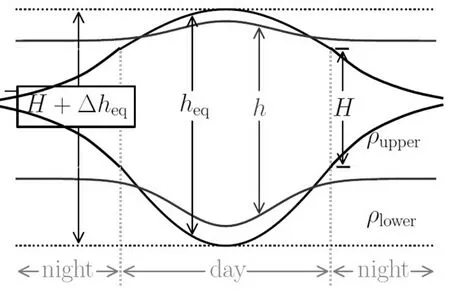
图3 浅水模型应用于热木星大气环流的图示[41].图中实线分别表示实际的高度场h和辐射平衡下的高度场heq.Fig.3 A schem e of Shallow-w ater m odel app lied to a hot Jup iter’s atm ospheric circu lation[41].The solid lines rep resent the actua l height field h and rad iative equ ilib rium heigh t field heq.

假设大气满足均衡理论(Isostasy)[45],则下层中一定深度以上的总质量保持恒定,斜压波所在处的上层自由面和分界面向两个方向弯曲,如图3所示.均衡假设意味着下层没有水平压力梯度,也就没有水平速度,但是有垂直速度,质量可以在两层之间传输.上层大气的动量方程写作:

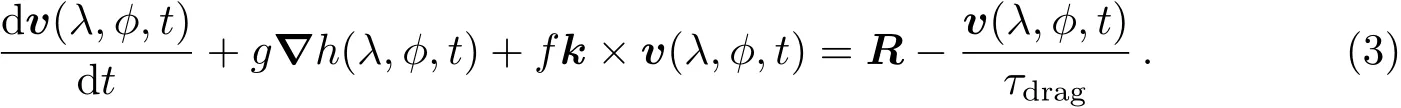
其中h为上层大气的厚度,R为传入上层的动量,τdrag为阻力时标,这里不考虑大气阻力的细节过程,简单以−v/τdrag表示大气阻力项.上层大气的质量连续性方程写作:

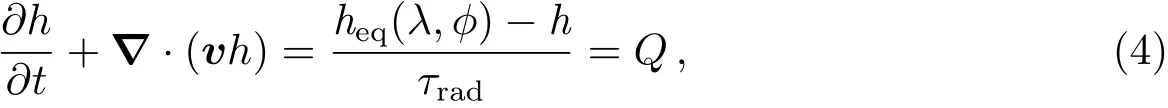
其中Q为能量传输项,Q>0表示加热,Q<0表示冷却,τrad为辐射时标.heq(λ,ϕ)为辐射平衡下的大气厚度场,因为热木星是同步自转,heq(λ,ϕ)不变,且一面永远是昼面,另一面永远是夜面,设星下点的(λ,ϕ)=(0◦,0◦),可以认为其中H是辐射平衡下的昼夜面平均大气厚度,∆heq是辐射平衡下的星下点处与平均值的大气厚度差值,如图3所示.

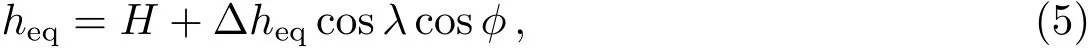
(4)式的意义为:当上层大气未达到辐射平衡时,质量将在两层间传输,使得h增大或减小.在辐射时标τrad内,h向heq弛豫,辐射时标τrad是模型的一个自由参数.我们可以结合大气3维背景来理解这种质量传输,在3维背景下h代表等熵面以上的质量柱.在加热至局部辐射平衡的区域(即Q>0),流体熵增,并高于参考等熵面,使得h增大.类似地,在冷却的区域,即Q<0的区域,流体降到参考等熵面以下,使h减小.

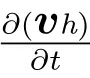
在本文中,我们根据Showm an等人的方法[39]对程序包STSWM[44]加以修改.原始程序包STSWM的控制方程是浅水方程的基本形式,即(1)和(2)式,我们在程序包中添加了力学项,依上述内容将控制方程分别改为(3)式和(4)式,使之符合热木星的大气特征.

3 谱变换算法

STSWM采用谱变换算法在球坐标系下解浅水方程组.在球坐标系下求解浅水方程,广泛采用的是谱变换方法.谱变换方法的基本思想[44]是先在类似有限差分法的格点中就地估算所有非线性项,然后将这些项通过傅立叶变换和高斯积分转到波数空间,如(6)式所示.

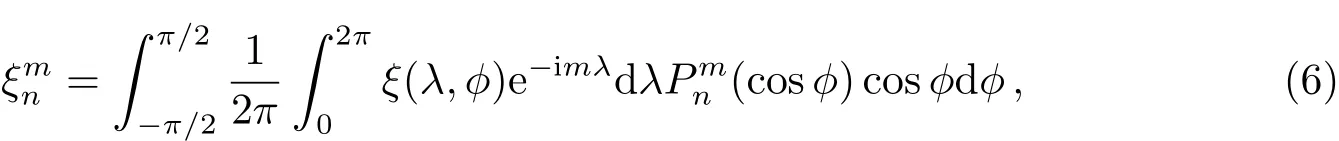
上式表示方程组中任意待求量ξ(λ,ϕ)可以通过傅立叶变换和高斯积分展开成一段截断的球谐函数之和,式中是连带勒让德多项式.

在波数空间计算各线性项和导数,可将求导运算简化为乘积运算.运算结束时,再将变量从波数空间转回实际空间,如(7)式所示:

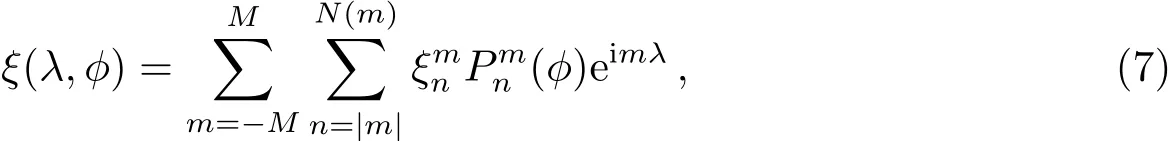
式中M为最大傅里叶波数,N(m)为连带勒让德多项式的最高次.谱变换方法将动量方程写为涡度方程和散度方程的形式,采用速度和纬度余弦乘积来取代速度,且球面网格采用高斯格点,不包含南北极点,可以避免“极点问题”(球坐标系下两极点为奇点).浅水方程的解代表多种大气运动类型,包括Rossby波、Kelvin波等.

我们在程序中选择谱截断T170,对应全球512×256的网格.该系统对初始条件不敏感[47],所以可以将初始条件简单设为一个静止的厚度均匀为H的上层大气,模型的自由参数设置参考了Liu和Showman的研究[47],H=200 km,τdrag=τrad=1 d,∆heq/H=0.01,并且运行各算例至大气环流结构达到稳定状态,此时得到的大气厚度分布h(λ,ϕ)是我们感兴趣的结果,它是大气环流和恒星辐射共同作用的结果,这里将其称为大气环流平衡图案.

若将稳定状态下的热木星大气厚度h(λ,ϕ)在朝向观测者的半球进行积分,得到的积分值(t)可视为热木星红外辐射通量的相关量[48]:

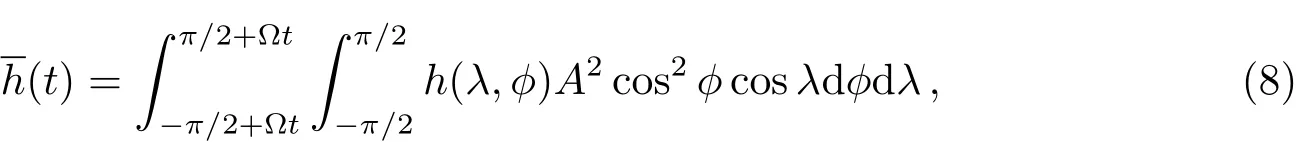
其中A为热木星半径,由此还可模拟出理论的红外相曲线.

4 结果

Showman和Guillot[25]在2002年最先预测了热木星HD189733b上存在大气环流运动,并提出这一现象会反映在红外相曲线和光谱上.该预测已被Spitzer空间望远镜对热木星HD 189733b的红外观测所证实[7−8],意味着该热木星上确实存在超自转气流.我们采用热木星HD 189733b的属性参数(见表1)计算得到其大气环流的平衡图案(如图4左)与Liu和Showman的计算结果[47](图4右)基本一致,因此验证了我们对STSWM程序包的修改是可信的.

表1 热木星HD 189733b的属性参数Tab le 1 T he p aram eters for HD 189733b

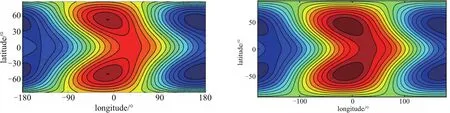
图4 对热木星HD 189733b的计算结果比较:我们的结果(左图)与Liu和Showm an的计算结果[47](右图)基本一致.Fig.4 Ou r sim u lation resu lts for HD 189733b basica lly agree with those of Liu&Showm an’s.The left panel:ou r resu lts,the righ t panel:Liu&Showm an’s resu lts[47].

接下来,我们用3组算例分别展示热木星HD 189733b的3个属性(半径A、自转速率Ω、表面重力加速度g)对于大气环流平衡图案以及相曲线相位的影响.在每组算例中,每次只改变一个变量值,保持另外两个变量不变.半径A、自转速率Ω、表面重力加速度g的取值均在热木星的典型值范围内.我们对结果数据进行了归一化处理,以便比较各算例的环流平衡图案和相曲线相位差异.下面我们将逐一介绍计算结果.

4.1 热木星半径的影响

第1组算例研究不同半径对于热木星大气环流平衡图案和红外相曲线相位的影响.这组算例的自转速率、表面重力加速度相同.各算例的参数取值如表2所示,自转速率Ω、表面重力加速度g取值与热木星HD 189733b一致.典型的热木星半径的量级在106–109m之间,所以算例的半径取值为8.20×106m、8.20×107m、8.20×108m、8.20×109m.

表2 半径、自转速率、表面重力加速度3组算例各自对应的4个参数取值Tab le 2 Fou r va lues of rad ius,rotation rate,and su r face grav ity acceleration in the 3 group s of param eters

如图5左列所示,图中颜色深浅表示大气厚度h的大小,颜色越浅表示h越大,颜色越深表示h越小.大气厚度分布在总体上还是保持着昼面高夜面低的情况,可以理解为昼面热夜面冷.赤道上的大气厚度极大值代表赤道上的最热区域.

图案在北半球呈现西北-东南方向倾斜,在南半球呈现西南-东北方向倾斜,赤道上的最热区域向东偏离了星下点,与Showm an等人的结果一致[39].如第1节中所述,这种现象产生的机制可能是行星尺度波的相互作用.昼夜面的巨大温差引发了持续的行星尺度的波,在低纬度生成了赤道Kelvin波,Kelvin波表现向东的群速度,在一个存在持续动力和阻尼的环流运动中将导致赤道附近的热学图案有向东的相位移动.同时,赤道Rossby波在Kelvin波的南北两侧生成,表现向西的群速度,因此中纬度的热学图案将出现向西的相位移动.

图5右列是根据(8)式算得的理论红外相曲线,0相位代表凌星主掩的时刻,相位1和−1代表凌星次掩的时刻.由图5可见,A 1、A 2、A 3、A4算例中环流平衡图案均呈现出相同程度的赤道超自转现象,相应的理论红外相曲线极大值、极小值的相位也相同,极大值的相位在凌星次掩之前,极小值的相位在凌星主掩之前.

由算例A1、A 2、A 3、A 4的结果可以看出,在热木星其他属性不变的情况下,半径变化对于热木星大气环流平衡图案的影响可以忽略,进而对红外相曲线的极大值、极小值相位的影响也可以忽略.

4.2 热木星自转速率的影响

第2组算例研究不同自转速率对于热木星大气环流平衡图案和红外相曲线相位的影响.这组算例的半径、表面重力加速度相同,各算例的参数取值如表2所示,半径A、表面重力加速度g取值与HD 189733b一致.因为热木星的周期约为1–5个地球日,典型的热木星自转速率约在1.0×10−5–7.0×10−5s−1之间,所以这组算例的自转速率Ω取值为1.0×10−5s−1、2.0×10−5s−1、4.0×10−5s−1与6.0×10−5s−1,结果如图6所示.

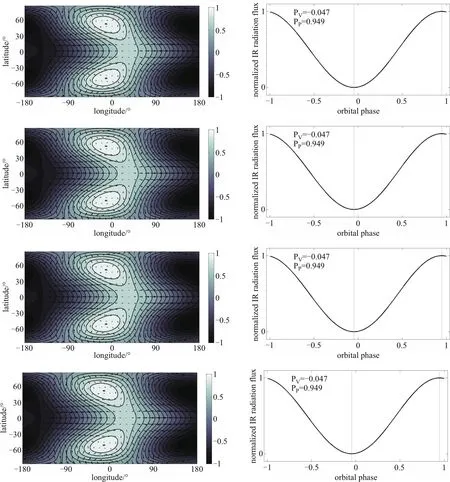
图5 由上到下依次是算例A 1、A 2、A 3、A 4的大气环流平衡图案(左)和红外相曲线相位(右),左图中箭头表示大气的速度场.令星下点经纬度为(0◦,0◦).右图中PV表示红外相曲线最小值相位,PP表示最大值相位.结果数据进行了归一化处理,以便比较各算例的环流平衡图案和相曲线相位差异.Fig.5 The equilibrated pattern of atm ospheric circu lation(left)and the phases of peak and valley in IR phase cu rve(righ t)of Cases A 1,A 2,A 3,and A 4 are show n from top to bottom,resp ectively.A rrow s rep resent atm ospheric velocity field in left-side figu res.Substellar p oin t is at longitude,latitude(0◦,0◦). In righ t-side figu res,PVrep resen ts the phase of va lley va lue in IR phase cu rve,w h ile PPrep resen ts the phase of peak value.The resu lts are norm alized for easier com parison.

图6中,算例Ω1的大气环流平衡图案接近于辐射平衡下heq的情况,整个图案虽然出现了向东的相位移动,但是赤道没有出现明显的超自转流,理论上红外相曲线的极大值的相位在凌星次掩之前,极小值的相位在凌星主掩之前.

算例Ω2的大气环流平衡图案出现了明显的赤道超自转流,赤道上的最热区域向东偏离了星下点,而中纬度区域的图案相位出现了向西移动,理论上红外相曲线的极大值的相位在凌星次掩之前,极小值的相位在凌星主掩之前.

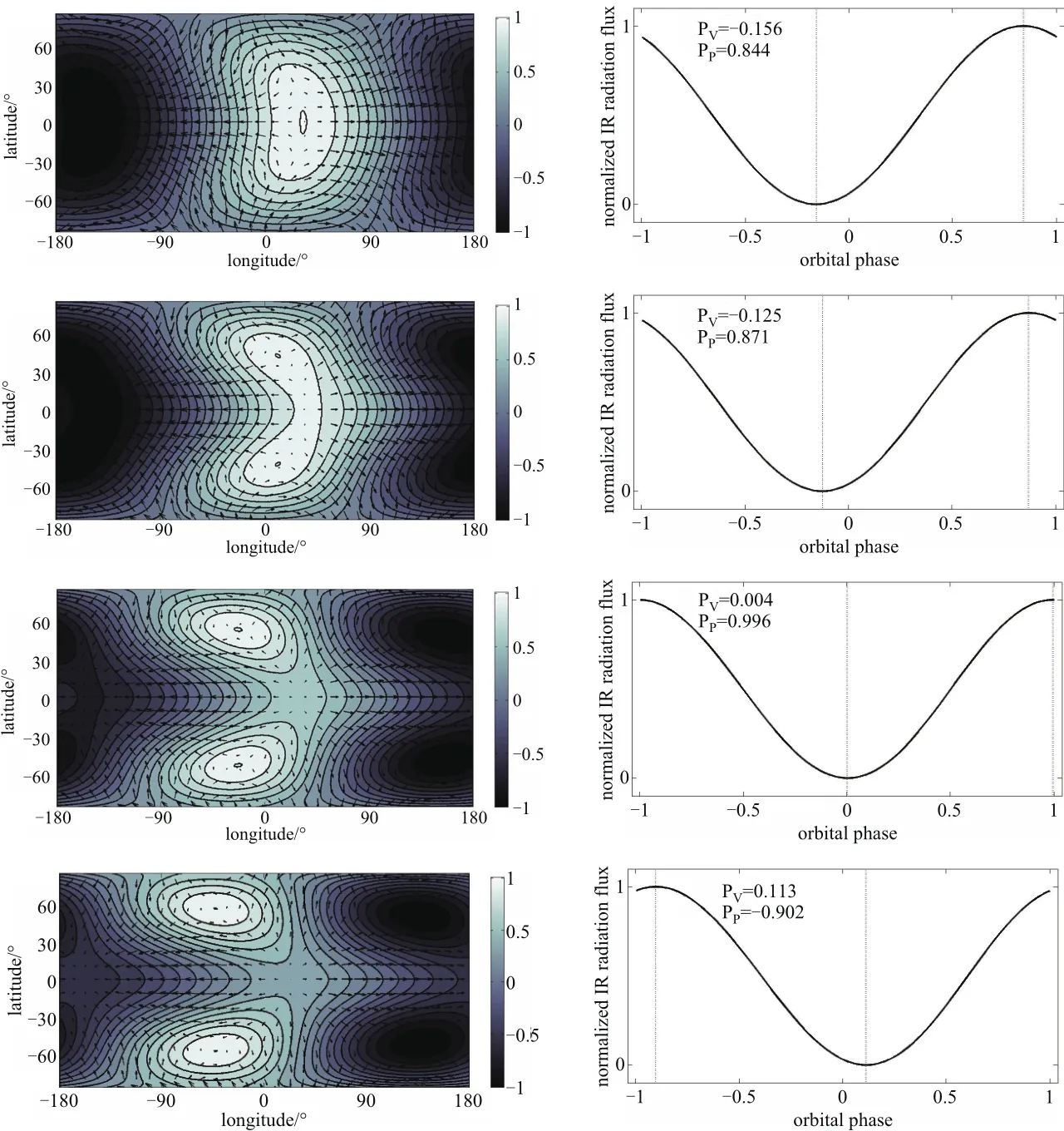
图6 由上到下依次是算例Ω1、Ω2、Ω3、Ω4的大气环流平衡图案(左)和红外相曲线相位(右).图中各线条和符号含义同图5.Fig.6 Equ ilib rated pattern of atm ospheric circu lation(left)and phases of peak and valley in IR phase cu rve(right)of CasesΩ1,Ω2,Ω3,andΩ4 are show n from top to bottom,resp ectively.T he m ean ings of cu rves and sym bo ls are the sam e as show n in Figu re 5.

算例Ω3的大气环流平衡图案中的赤道超自转流更加明显,赤道上最热区域向东偏离星下点的程度更大,中纬度区域的图案相位向西移动的程度也更大.理论红外相曲线的极大值相位在凌星次掩之前,而与算例Ω1、Ω2不同的是,算例Ω3的极小值的相位在凌星主掩之后.

算例Ω4大气环流平衡图案上的赤道超自转流与算例Ω3的一样明显,中纬度图案相位向西移动的程度比算例Ω3更严重.理论红外相曲线相位与算例Ω1、Ω2完全不同,算例Ω4的极大值的相位在凌星次掩之后,极小值的相位在凌星主掩之后.

由算例Ω1、Ω2、Ω3、Ω4的结果可以看出,在热木星其他属性不变的情况下,自转速率变化对于热木星大气环流平衡图案的影响较大.热木星自转速率越大,赤道超自转流越明显,赤道最热区域向东偏离星下点的程度越严重,中纬度向西的相位移动也越严重.进而在红外相曲线上的反映也不同,极值的相位相对于凌星主掩和次掩的位置不同.

4.3 热木星表面重力加速度的影响

第3组算例研究不同表面重力加速度对于热木星大气环流平衡图案和红外相曲线相位的影响.这组算例的半径、自转速率相同.各算例的参数取值如表2所示,半径A、Ω取值与HD 189733b一致.典型的热木星表面重力加速度在100 m·s−2以内,所以算例的表面重力加速度分别取值为5.0m·s−2、20.0m·s−2、40.0m·s−2、80.0m·s−2.

如图7所示,g1、g2、g3、g4算例中环流平衡图案均呈现出相同程度的赤道超自转现象,相应的理论红外相曲线极大值和极小值的相位也相同,极大值的相位在凌星次掩之前,极小值的相位在凌星主掩之前.

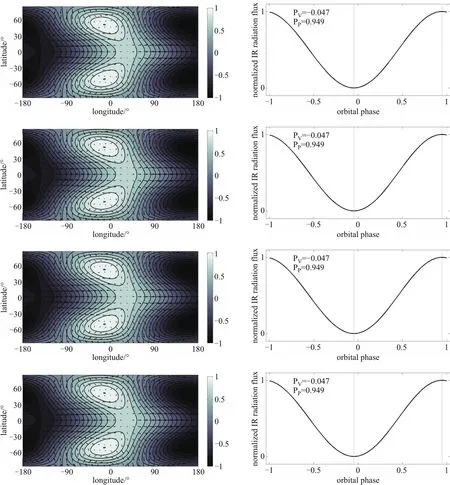
图7 由上到下依次是算例g1、g2、g3、g4的大气环流平衡图案(左)和红外相曲线相位(右).图中各线条和符号含义同图5.Fig.7 Equ ilib rated pattern of atm ospheric circu lation(left)and phases of p eak and va lley in IR phase cu rve(righ t)of Cases g1,g2,g3,and g4 are show n from top to bottom,resp ectively.T he m eanings of cu rves and sym bo ls are the sam e as show n in Figu re 5.

由算例g1、g2、g3、g4的结果可以看出,在热木星其他属性不变的情况下,表面重力加速度变化对于热木星大气环流平衡图案的影响可以忽略,进而对红外相曲线的极大值和极小值相位的影响也可以忽略.

5 讨论与总结

本文中各算例的大气环流平衡图案表明:由于赤道Kelvin波表现为向东的群速度,所以赤道出现向东超自转流,超自转现象把昼面热量向东传输到夜面.而Kelvin波两侧生成的Rossby波表现为向西的群速度,所以中纬度出现向西的相位移动,把昼面热量向东传输到夜面.

在热木星其他参数不变的情况下,半径、表面重力加速度变化对于热木星大气环流平衡图案的影响可以忽略,进而对红外相曲线的极大值和极小值相位的影响也可以忽略.但是,自转速率变化对于热木星大气环流平衡图案以及红外相曲线的影响较大.热木星自转速率越大,赤道超自转流越明显,赤道最热区域向东偏离星下点的程度越严重,中纬度向西的相移也越严重.随着热木星自转速率增大,赤道以外的全球大部分区域的平衡图案相位西移,导致理论红外相曲线极大值出现在凌星次掩之后,极小值出现在凌星主掩之后.

在未来的热木星红外相曲线观测中,本文的研究有助于对一些可能出现的观测结果做出预测.在热木星红外相曲线的长期观测中,若极大值和极小值的相位发生了明显变化,则热木星的自转速率改变有可能是原因之一.实际上,热木星的大气环流平衡图案及相曲线相位还与热木星大气成分、所受辐射量、是否同步自转等因素相关,这将在今后的研究中进行讨论.

[1]Dong Y,Ji J H.ScChG,2012,55:872

[2]董瑶,季江徽.天文学报,2013,56:350

[3]Dong Y,Ji J H.ChA&A,2014,38:186

[4]Dong Y,Ji J H.M NRAS,2013,430:951

[5]Showm an A P,Cho J Y,M enou K.T he C lim ate of the A rctic.Tucson:Sp ringer In ternationa l Publish ing,2009:3508-3517

[6]K nu tson H A,Charbonneau D,A llen L E,et a l.Natu re,2007,447:183

[7]Knutson H A,Charbonneau D,Cowan N B,et al.Ap J,2009,690:822

[8]Charbonneau D,K nu tson H A,Barm an T,et a l.A p J,2008,686:1341

[9]Harrington J,Hansen B M,Luszcz S H,et al.Science,2006,314:623

[10]Cow an N B,A gol E,Charbonneau D.M NRAS,2007,379:641

[11]Sw ain M R,Vasisht G,T inetti G,et al.Ap J,2009,690:L114

[12]C rossfield I J M,Hansen B M S,Harrington J,et al.A p J,2010,723:1436

[13]Heng K,Showm an A P.AREPS,2014,43:1

[14]Seager S.Exop lanet A tm ospheres.P rinceton:P rinceton University P ress,2010:40

[15]M arley M S,G elino C,Stephens D,et a l.A p J,1999,513:879

[16]Sudarsky D,Bu rrow s A,Pinto P.Ap J,2000,538:885

[17]Bu rrow s A,Sudarsky D,Hubeny I.A p J,2004,609:407

[18]Barm an T S,Hauschild t P H,A llard F.Ap J,2005,632:1132

[19]M adhusudhan N,Bu rrow s A.A p J,2011,747:25

[20]Showm an A P,Fortney J J,Lian Y,et a l.A p J,2009,699:564

[21]Heng K,Frierson D M W,Phillipps P J.M NRAS,2011,418:2669

[22]Rauscher E,M enou K.A p J,2012,750:96

[23]Perna R,Heng K,Pon t F.A p J,2012,751:59

[24]Dobbs-D ixon I,A go l E.M NRAS,2013,435:3159

[25]Showm an A P,Gu illot T.A&A,2002,385:166

[26]Cooper C S,Showm an A P.A p J,2005,629:L 45

[27]Cooper C S,Showm an A P.A p J,2006,649:1048

[28]Showm an A P,Coop er C S,Fortney J J,et al.A p J,2008,682:559

[29]Dobbs-D ixon I,Lin D N C.A p J,2008,673:513

[30]M enou K,Rauscher E.A p J,2009,700:887

[31]Rauscher E,M enou K.A p J,2010,714:1334

[32]Dobbs-D ixon I,Cumm ing A,Lin D N C.A p J,2010,710:1395

[33]Th rastarson H T,Cho J.A p J,2010,716:144

[34]Lew is N K,Showm an A P,Fortney J J,et a l.A p J,2010,720:344

[35]Perna R,M enou K,Rauscher E.Ap J,2010,719:1421

[36]Heng K,M enou K,Phillipps P J.M NRAS,2011,413:2380

[37]Cho J Y K,M enou K,Hansen B M S,et a l.A p JL,2003,587:L 117

[38]Cho J Y K,M enou K,Hansen B M S,et a l.A p J,2008,675:817

[39]Showm an A P,Po lvan i L M.A p J,2011,738:71

[40]Showm an A P,Fortney J J,Lew is N K,et al.Ap J,2013,762:24

[41]Perezbecker D,Showm an A P.A p J,2013,776:201

[42]Showm an A P,Lew is N K,Fortney J J.A p J,2015,801:1816

[43]K asp i Y,Showm an A P.A p J,2015,804:60

[44]Hack J J,Jakob R.Nationa l Cen ter for A tm ospheric Research Techn ica l Note NCAR/TN-343+STR. Bou lder:Nationa l Center for A tm ospheric Research,1992

[45]G ill A E.A tm osphere-O cean Dynam ics.London:A cadem ic P ress,1982

[46]Shell K M,Held IM.JA tS,2004,61:2928

[47]Liu B,Showm an A P.Ap J,2013,770:42

[48]Zhang X,Showm an A P.A p J,2014,788:1

The In fluence A nalysis of a Hot Jup iter’s Property on Its Phases of Peak and Valley in IR Phase Curve

TIAN Lei1,2JI Jiang-hui1,3

(1 Pu rp le M oun tain O bserva to ry,Chinese A cadem y of Scien ces,Nan jing 210008) (2 Un iversity of Chinese Academ y of Scien ces,Beijing 100049) (3 K ey Labo ra to ry of P laneta ry Scien ces,Chinese A cadem y of Scien ces,Nan jing 210008)

We investigate the influence of a hot Jupiter’s property on its equilibrated pattern of atmospheric circu lation(EPAC)and its phases of peak and valley in in frared phase curve(IRPC)with the shallow-water model.The influences of a hot Jupiter’s radius,rotation rate,and surface gravity acceleration,respectively,are extensively explored in this work.In the simulations,we adopt the physical parameters sim ilar to those of HD 189733b.The results show that the rotation rate of the hot Jupiter may play a vital role in its EPAC and IRPC,whereas the influence of its radius and surface gravity acceleration is negligible.Thereby,we can in fer that if the phases of peak and valley in IR phase curve vary significantly in the long-term observations,the variation of the hot Jupiter’s rotation ratemay act as one of the potential causes.

celestialmechanics,hydrodynam ics,p lanets and satellites:atmospheres, methods:numerical

P138;

A

10.15940/j.cnki.0001-5245.2016.06.006

2016-04-11收到原稿,2016-04-26收到修改稿

∗国家自然科学基金项目(11273068,11473073)、中国科学院战略性先导科技专项(B类)(XDB09000000)、中国科学院新兴与交叉学科布局试点项目(KJZD-EW-Z001)和紫金山天文台小行星基金会资助

†764955965@qq.com

‡jijh@pm o.ac.cn