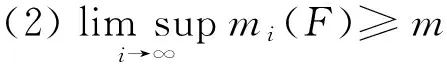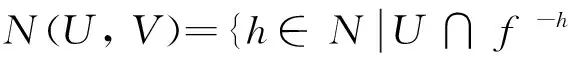正上密度回归点集的若干性质
曹 毅, 吴晓荣
(1. 江苏理工学院数理学院, 江苏 常州 213001; 2. 南京外国语学校, 江苏 南京 210008)
正上密度回归点集的若干性质
曹 毅1, 吴晓荣2
(1. 江苏理工学院数理学院, 江苏 常州213001; 2. 南京外国语学校, 江苏 南京210008)
摘要:令X为紧致度量空间,f:X→X为连续映射, 讨论正上密度回归点与支撑点的关系,并证明当正上密度回归点集稠密时, 可迁系统等价于E系统.
关键词:E系统; 支撑点; 正上Banach密度回归点
0引言
拓扑空间中连续自映射的周期点、 回归点、 非游荡点及映射混沌性是拓扑动力系统的重要研究内容. 在这些方面,许多学者已经进行了广泛的研究,做出了很多贡献,而从纯粹的拓扑角度看,回归点集的轨道才是最重要的.
设(X,d)是紧致度量空间,f:X→X是连续映射. 若点x的轨道无限次地进入它的任一邻域,则称之为f的回归点. 根据点x的轨道进入邻域的不同频数,可以有不同的回归. 文献[1]给出了一种特殊的回归现象——正上Banach密度回归. 讨论正上Banach密度回归点,得出正上Banach密度回归点集在迭代作用的不变性,并给出正上Banach密度回归点集稠密时f拓扑可迁的等价条件.
1相关定义

定义2设A={a1, a2, …},其中a1 定义4如果(X, f)拓扑可迁且存在有全支撑的不变测度,则称(X, f)为E系统. 如果存在x∈X,对于任意ε>0,有m(V(x, ε))>0,则称x为m∈M(X, f)的支撑点. Sm表示m所有支撑点的集合. 如果对于任意ε>0,存在m∈M(X, f),使得m(V(x, ε))>0,则称x∈X为f的支撑点. 2正上密度回归点集与支撑点集 引理3[4]设(X, f)为一动力系统,E、 F分别为X的开子集和闭子集,m,mi∈M(X),i=1, 2, …,且mi在ω*拓扑下收敛到m,则有 引理5[6]设(X, f)为一动力系统,则以下等价: (1) f拓扑可迁; (2) f 为满射且Trans(f)≠Ø; 定理1设(X, f)为一动力系统: 所以x为μ的支撑点,从而x为f的支撑点. 在上式中取g=χV,其中χV为V上的特征函数. 从而有: 即 3正上密度回归点集稠密的等价条件 定理3设(X, f)为一动力系统,下列条件等价: (2) (X, f)是E系统; 证明充分性显然. 因为N(W, W)⊃N(x, W)-N(x, W),由引理6得N(W, W)为Syndentic集. 而当fi(W)∩W≠φ时,fi+n(U)∩V⊃fi+n(W)∩fi(W)⊃fn(fi(W)∩W)≠Ø, 即 于是N(U, V)为Syndentic集,f是拓扑强遍历的. 引理7[7]设X为一紧致度量空间,f:X→X是连续满射,则f拓扑弱遍历且不是敏感依赖于初始条件的充分必要条件是f是一致几乎周期的极小同胚. 引理8[8]设X为一紧致度量空间,f:X→X是连续满射,则f一致几乎周期的充分必要条件是f等度连续. 参考文献: [1] YIN J D, ZHOU Z L. Positive upper density points and chaos[J]. Acta Mathematics Scientia, 2012, 32(4): 1 408-1 414. [2] AKIN E. The general topology of dynamical systems (graduate studies in mathematical sciences)[M]. New York: American Mathematical Society, 1993. [3] AKIN E. Recurrence in topological dynamics: furstenberg families and ellis actions[M]. New York: Plenum Press, 1997: 96. [4] WALTERS P. An introduction to ergodic theory[M]. New York: Springer Verlag, 1982. [5] 周作领. 弱几乎周期点和测度中心[J]. 中国科学(A辑), 1992, 6(6): 572-581. [6] KOLYADA S, SNOHA L. Some aspects of topological transitivity: a survay[J]. Grazer Math Ber, 1997, 334(1):3-35. [7] 杨润生. 拓扑遍历映射[J].数学学报,2001, 44(6): 1 063-1 068. [8] AUSLANDER J. Minimum flows and their extensions[M]. North Holland: Elsevier Science Ltd , 1988. (责任编辑: 洪江星) Some properties of positive upper density recurrence points CAO Yi1, WU Xiaorong2 (1. School of Mathematics and Physics, Jiangsu University of Technology, Changzhou, Jiangsu 213001, China; 2. Nanjing Foreign Language School, Nanjing, Jiangsu 210008, China) Abstract:Let X be a compact metric space and f:X→X a continuous onto maps. This paper discusses the relationships of the positive upper Banach density recurrence point and the support point, and proves that a topologically transitivity system is equivalent to a E-system when the set of positive upper Banach density recurrence points is dense. Keywords:E-system; support point; positive upper Banach density recurrence points DOI:10.7631/issn.1000-2243.2016.03.0401 文章编号:1000-2243(2016)03-0401-04 收稿日期:2013-11-22 通讯作者:曹毅(1978-),讲师,主要从事方向动力系统与遍历理论方面的研究,cyy7812@163.com 基金项目:国家自然科学基金资助项目(11102076); 江苏理工学院青年科研基金资助项目(KYY12023) 中图分类号:O189.3 文献标识码:A