发电机运动轨迹预测理论的研究

胡雪凯，梁纪峰，张 乾，刘翔宇

(1.国网河北省电力公司电力科学研究院，河北 石家庄 050021；2.国网河北省电力公司检修分公司，河北 石家庄 050070)

发电机运动轨迹预测理论的研究

胡雪凯1，梁纪峰1，张 乾2，刘翔宇1

(1.国网河北省电力公司电力科学研究院，河北 石家庄 050021；2.国网河北省电力公司检修分公司，河北 石家庄 050070)

广域测量系统的发展，为根据实测电力系统轨迹进行暂态不稳定性的紧急控制提供了可能。利用实时数据进行超实时预测能尽早投入控制措施，阻止失步的发生。因此，研究高精度长时间的轨迹预测具有重要意义。从发电机运动方程出发，导出了适用于电力系统的滚动自记忆预测方法。该方法先用三角函数拟合不平衡功率，然后由不平衡功率预测角速度，最后由自记忆公式预测功角。IEEE9节点系统的仿真计算结果表明，该方法可以很准确地预测未来至少0.5 s的功角轨迹，同三角函数、自回归预测相比，具有预测精度高、预测时间长的优点。

电力系统；功角；自记忆预测；三角函数预测；自回归预测

0 引言

广域相量测量系统(Wide Area Measurement System，WAMS)在电力系统的广泛应用，使得动态过程中机组的运动轨迹可以直接测量而不必依赖于传统的数值计算，这无疑为电力系统的实时紧急控制提供了新的发展契机[1-5]。在同一参考时间下，互相大电网的各项实时信息可以通过 WAMS获取，且数据更新速度达到毫秒级, 为电力系统的暂态不稳定性的实时识别提供了可能。

但是，如果只是利用WAMS实测的轨迹信息，在得出系统失稳的判断后才进行控制，往往无法阻止失步的发生，电力系统已转入失步解列再同步的过程，已经遭受了巨大的损失。所以，需要对轨迹进行准确的超实时预测，尽早地得出系统是否稳定的结论，才能为紧急控制赢得更多的时间。另外，广域信息在测量和传输过程中，可能存在部分缺失或延迟，对轨迹进行超实时预测还能起到弥补信息缺失和补偿延迟的作用[6-9]。

如何对发电机运动轨迹进行预测一直是电力科技工作者多年来努力寻求的目标。文献[10]采用计算机手段进行快速仿真，利用WAMS提供的信息更新计算初值，该方法必须基于系统故障后各元件的机电暂态模型和参数，然而这些数据往往是难以准确获得的；文献[11-13]分别使用了样条函数插值法、三角函数拟合法、自回归预测法，根据实测的状态信息实时辨识和滚动刷新预测模型的参数，以此来预测未来系统的轨迹，这类方法的优点是不依赖于系统的结构和参数，但它们都属于经验性预测，预测模型没有建立在符合物理规律上的动力学微分方程，缺乏机理性，导致预测精度不够；文献[14]尝试使用自组织映射神经网络的方法进行轨迹预测，这类方法的缺点是应用于实际时，训练的样本难以获得，而且训练过程相对困难。

本文从发电机的微分运动方程出发，导出了其运动轨迹的自记忆滚动预测方法，该方法在计及历史测量信息对未来影响的同时，还考虑了其高阶状态量变化对未来产生的影响。IEEE9节点系统的仿真结果表明，本文所提方法能够准确预测未来至少0.5 s的发电机运动轨迹，同三角函数、自回归预测相比，其预测精度更高、预测时间更长。

1 发电机运动方程及轨迹特性

多机电力系统同步参考坐标下的运动方程可以表示为

式中：di为发电机i的转子角；D wi为发电机i的转子角速度；Mi为发电机i的惯性时间常数；Pmi、Pei为机械输入功率、电磁输出功率； Di为阻尼因子；DPi= Pmi- Pei称为不平衡功率。

式(1)中的id、iwD 和iPD 可以实时测量，其中id二阶连续，iwD 一阶连续，iPD 代表了角加速度，属于高阶量，在系统发生离散操作时可以突变，但其在各次离散操作间保持连续；并且功角、角速度、角加速度之间遵循动力学关系。总之，电力系统的运动方程是一个非线性动力学方程。

计及发电机的调节器和调速器后，iPD 不再是正弦曲线，其变化情况比较复杂，但需要指出的是：不平衡功率的变化并不是毫无规律的随机变化，考虑到电力系统的实际情况，iPD 曲线具有低频拟周期性质，一段时间内的轨迹不平衡功率能够用三角函数拟合。

2 采用自记忆方法的轨迹预测

由于功角摇摆轨迹满足狄利克雷条件，文献[8]中采用三角函数对功角曲线进行预测，其三阶形式为；自回归也是一种轨迹预测的方法，它用于预测变量在固定的时间间隔内有很高相关系数的情形，其二级方程式为dt= b0+ b1dt-1+ b2dt-2+ e[15]。然而，以上两种方法的预测时长和精度都不够理想。

自记忆预测是从微分运动方程出发，与一个记忆函数作内积，将历史信息反映到微分方程中，在计算中具有良好的精度和稳定性[16-17]。它适用于如下形式的微分动力系统：

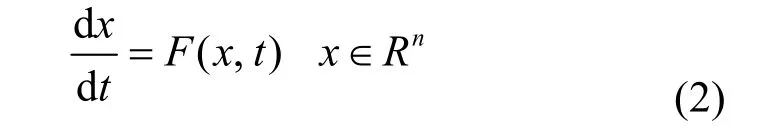
对应的离散表达式为

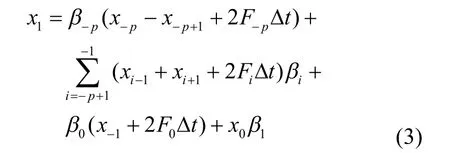
将式(2)与发电机运动方程(1)相比不难看出，d对应x，0w wD 对应 (,)Fxt,其三阶形式为

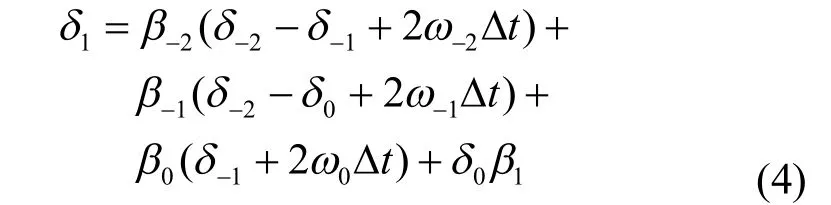
然而，这里的问题在于，式(3)右端的所有F(x,t)在常规自记忆预测中都是已知，或可以通过计算获得，但对于电力系统，式(4)中与 F (x,t)对应的 w0D w 只能获得当前时刻和之前时刻的测量数据，下一时刻的 w0D w 是未知的，而且无法准确计算出来，这样，仅仅下一时刻的功角 d1是可预测的，第二个时刻的功角 d2就已经不能预测，更不用说进行多步预测，显然这不是我们所预期的。

为了使自记忆应用到电力系统时能进行多步预测，有必要先对0w wD 进行预测。将运动方程(1)的第二式化为差分形式可得：

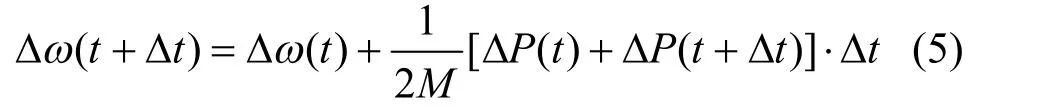
与上面预测功角的问题类似，要预测 wD ，就必须先预测 PD 。根据上一节对不平衡功率的分析，可以由

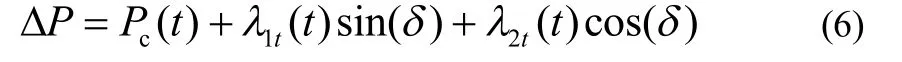
实现对 D P 的预测，其中 Pc(t) ,l0( t) ,l1(t) ,l2(t )为时变参数。针对某固定时刻的运行状态，只要系统不发生大的扰动或操作，可认为参数在短时间内保持恒定，也就是说，仅需用最小二乘法进行一次参数辨识，此后认为它们定常不变。

总结上面的讨论，可以根据之前时刻的 di和Dwi由式(4)预测下一时刻的 di+1，然后根据 di+1由式(6)预测下一时刻的 D Pi+1，再根据 D Pi和 D Pi+1由式(5)预测下一时刻的 D wi+1，于是就可以由 di+1，D wi+1返回式(4)预测第二个时刻的 di+2，如此一直滚动预测到所需时刻。流程图如图1。

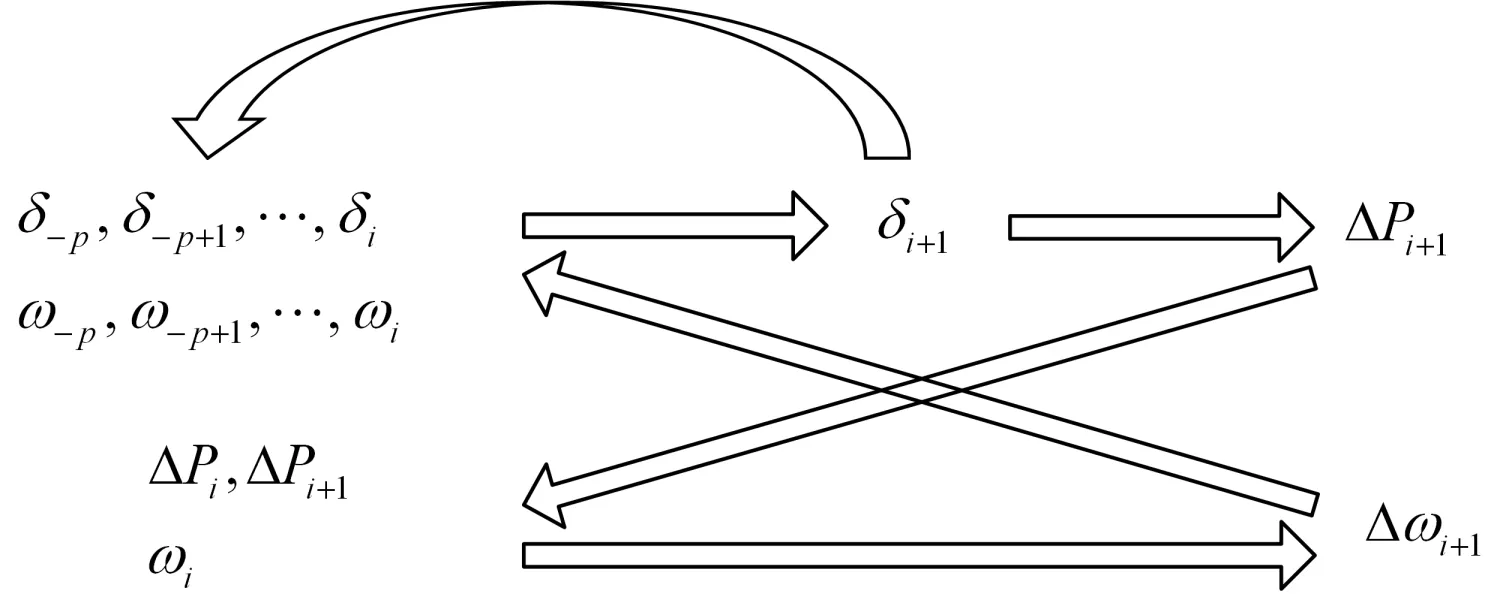
图1 自记忆预测流程Fig. 1 Process of self-memory prediction

3 仿真计算

为验证自记忆预测方法的优越性，在 PSASP中，以图2所示的IEEE9节点系统为例进行仿真计算。

图2 IEEE9系统Fig. 2 IEEE9 system

故障设为5号母线和7号母线之间的线路在靠近5号母线处发生三相短路。

故障切除时间为0.36 s时，功角发生单摆，保持稳定。0.4~0.5 s为采样时段，对于发电机G2，3种方法的预测轨迹及实际轨迹如图3(a)所示(以G1作为参考机，测量点数N=10，图中用“*”表示测量点)。

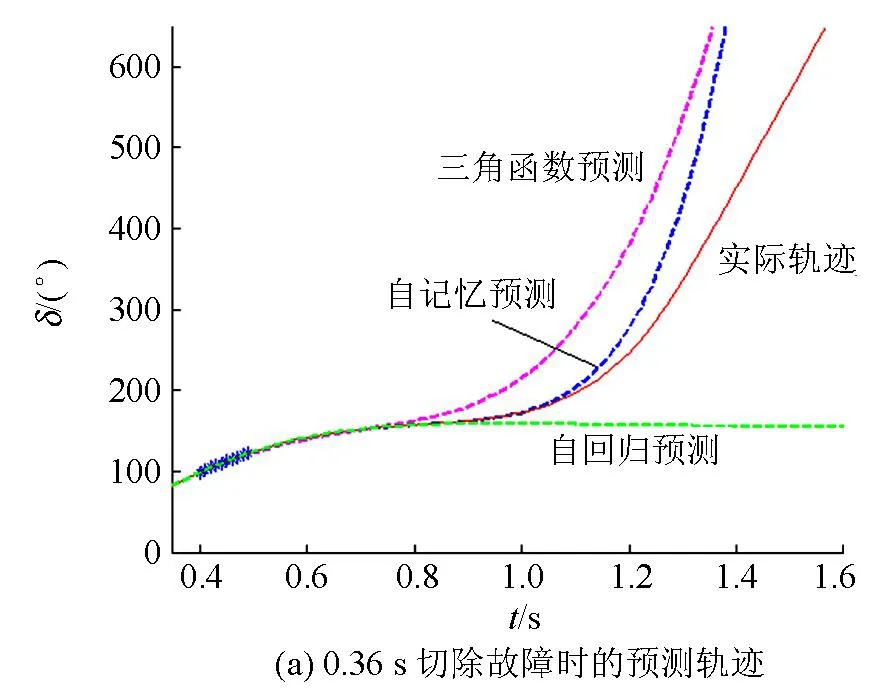
图3 数据窗长T0=100 ms，测量点数N=10，测量间隔Dt=10 msFig. 3 Data window T0=100 ms, point N=10, interval Dt=10 ms

故障切除时间为 0.30 s时，功角多摆失稳。0.4~0.5 s为采样时段，3种方法的预测轨迹及实际轨迹如图3(b)所示。

表1给出了3种方法在不同预测时间长度下的最大误差。

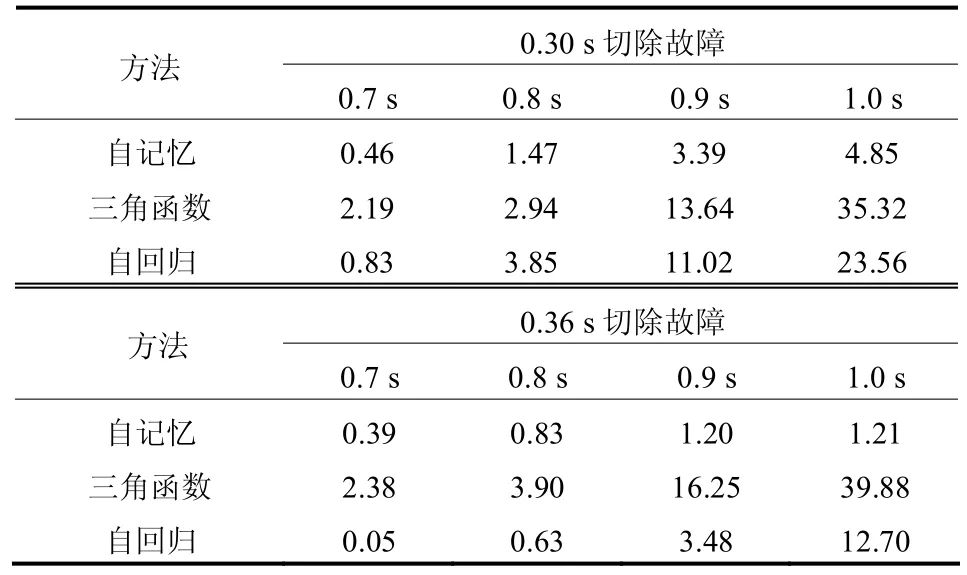
表1 不同预测时间长度下的最大误差Table 1 Maximum error of different prediction time length单位(º)

从图3及表1可以看出，对于以上3种方法，预测点越接近测量点，预测精度越高。其中，三角函数预测的效果较差；自回归预测在开始几个点处与自记忆预测相差不大，但随着预测时间的增长，自回归的误差迅速增大，并且不能反映出轨迹的发展趋势，而自记忆预测仍能保持较高的精度。如果将功角误差限定在 5°之内，自记忆可以预测未来0.5 s的轨迹；而三角函数和自回归只能预测0.3 s，可见自记忆的预测效果要远优于其他两种。

图4、图5给出了改变数据窗长度和测量点密度后的预测轨迹。

经过图3~图5的比较，发现在所有情况下，自记忆预测的精度和时间长度都要优于三角函数和自回归预测。尽管自记忆预测的运算量是3种方法中最大的，但在下一时刻的观测点到来之前，仍然能完成当前时刻的预测任务，因此计算量并不是要考虑的主要问题。

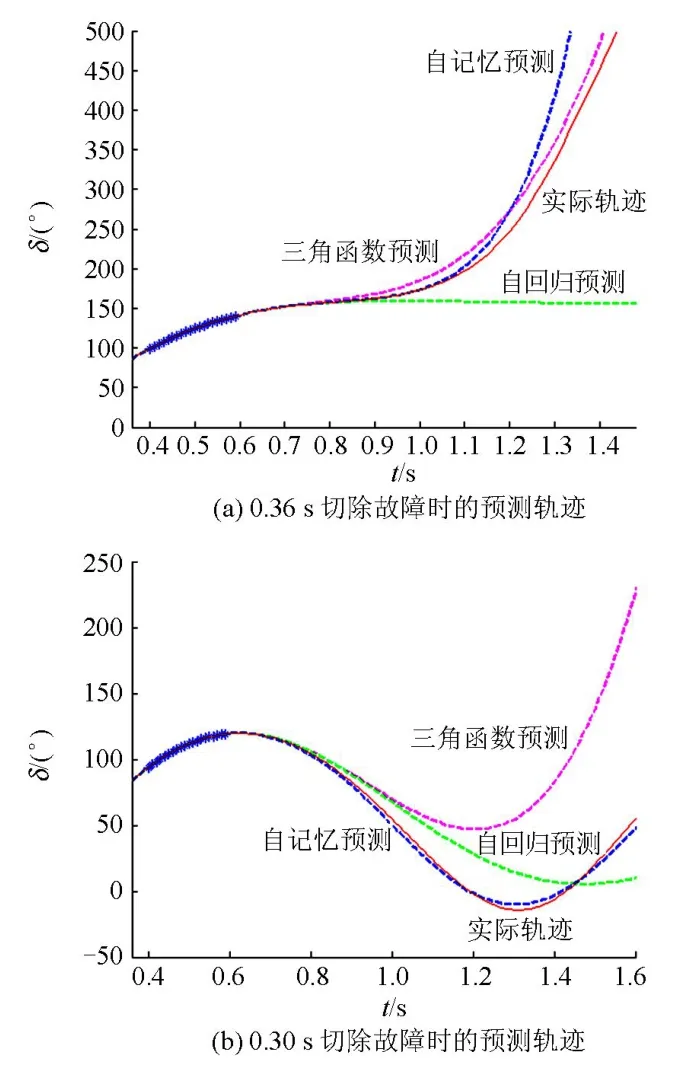
图4 数据窗长T0=200 ms，测量点数N=20，测量间隔Dt=10 msFig. 4 Data window T0=200 ms, point N=20, interval Dt=10 ms

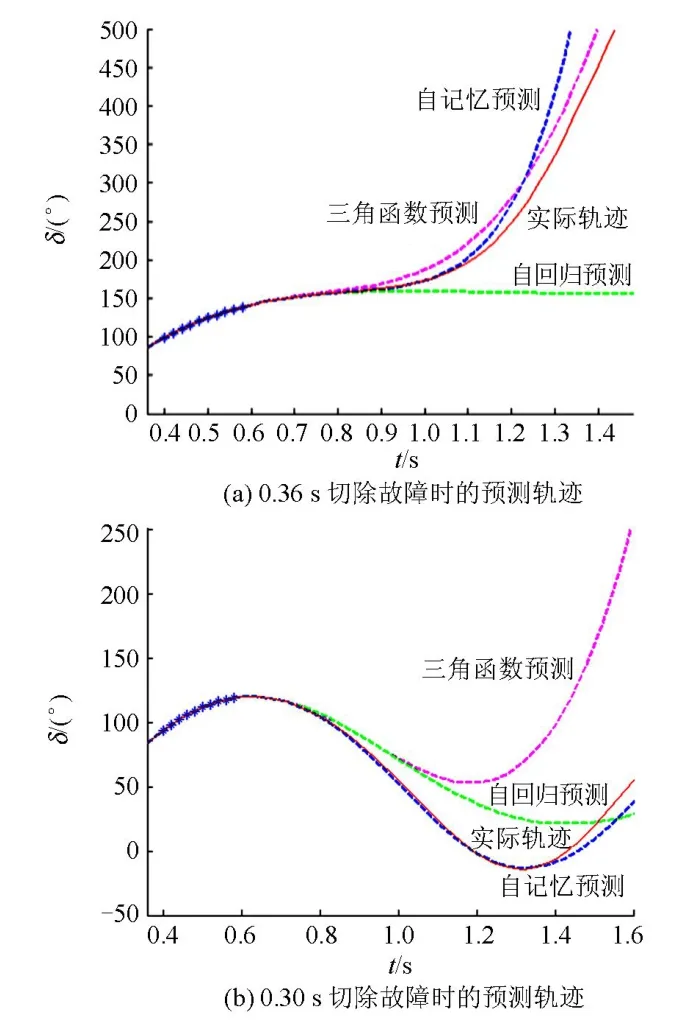
图5 数据窗长T0=200 ms，测量点数N=10，测量间隔Dt=20 msFig. 5 Data window T0=200 ms, point N=10, interval Dt=20 ms

对比图3和图4可以发现，当测量间隔不变(Dt= 10 ms)，窗长加倍(T0=200 ms)时，预测的准确性有明显的提高。对于多摆情况的预测，图3(b)在1.60 s时的误差已达42.1º，而图4(b) 预测到1.60 s时的误差仅为 7.2º；若误差限制在 5º以内，窗长T0=100 ms的图3(b)可以预测未来0.5 s的轨迹，窗长T0=200 ms的图4(b)则可以预测未来0.95 s的轨迹。

对比图4和图5可以发现，当窗长不变(T0=200 ms)，数据密度加倍时，预测的准确性也会有所提高。图5(b)在1.60 s时的误差为12.2º，而图4(b)在1.60 s时的误差仅为7.2º；若误差限制在5º以内，测量间隔Dt =20 ms的图5(b)可以预测未来0.88 s的轨迹，测量间隔Dt =10 ms的图 4(b)则可以预测未来0.95 s的轨迹。

由上面的比较可以得出，对于本文提出的滚动自记忆预测方法，测量数据窗越长，数据点越密，则准确预测的时间就越长，并且数据窗长度的影响较数据点密度更为突出，为了提高预测的精度和时长，可以适当增加数据窗长度和数据密度。

然而，数据窗的长度和数据密度并不能无节制地增加，而要考虑到实际条件的限制。目前测量装置的数据更新速度最快可达 20 ms，也就是说测量数据的密度最小为Dt =20 ms。同时，预测过程中要进行矩阵运算，当测量点数为N，预测点数为N'时，主要矩阵运算的乘法次数为(57N+7N')，加法次数为(39N-32+5N')，数据密度固定时，数据窗长度的加倍意味着点数加倍，从而使运算量加倍；另一方面，数据窗越长，则第一次预测开始的时间就会越迟，有可能在等待测量数据时系统就已经失步解列。因此，对于数据窗长也要加以限制，仿真表明窗长取200 ms左右较为合适，既能使运算量小，预测起始时间早，又能保证较高的预测精度和时长。

4 结论

本文基于发电机运动方程导出了多个状态量的自记忆滚动预测公式，它无需事先获得系统的参数和结构，在计及历史测量信息对未来影响的同时，还考虑了其高阶状态量变化对未来产生的影响。对IEEE9节点系统的仿真结果表明，该方法相对于三角函数、自回归等预测方法，无论在预测精度，还是在预测时间长度上，都是最优的。综合所有情况，当数据窗长l=200 ms，测量间隔Dt =20 ms，功角误差限定在5º之内时，自记忆至少可以预测未来0.5 s的轨迹变化情况。

[1] 卢志刚, 郝玉山, 康庆平, 等. 电力系统中实时相角测量中的参考相角预测[J]. 电力系统自动化, 1998, 22(8): 22-25. LU Zhigang, HAO Yushan, KANG Qingping, et al.Prediction of reference phase angle in real-time phase angle measurement of electric power system[J]. Automation of Electric Power Systems, 1998, 22(8): 22-25.

[2] 张保会. 加强继电保护与紧急控制系统的研究提高互联电网安全防御能力[J]. 中国电机工程学报, 2004, 24(7): 1-6. ZHANG Baohui. Strengthen the protection relay and urgency control systems to improve the capability of security in the interconnected power network[J]. Proceedings of the CSEE, 2004, 24(7): 1-6.

[3] 彭疆南, 孙元章, 程林. 基于受扰轨迹的紧急控制新方法[J]. 电力系统自动化, 2002, 26(21): 17-22. PENG Jiangnan, SUN Yuanzhang, CHENG Lin. A novel approach for transient stability emergency control based on perturbed trajectory[J]. Automation of Electric Power Systems, 2002, 26(21): 17-22.

[4] 张保会, 谢欢, 于广亮, 等. 基于广域轨迹信息的多机系统暂态不稳定性快速预测方法[J]. 电网技术, 2006, 30(19): 53-58. ZHANG Baohui, XIE Huan, YU Guangliang, et al. Fast prediction method for multi-machine system transient instability based on wide area trajectory information[J]. Power System Technology, 2006, 30(19): 53-58.

[5] 赵建成, 谢小荣, 穆钢. 基于 WAMS的电力系统暂态稳定的快速预测[J]. 继电器, 2005, 33(7): 1-5. ZHAO Jiancheng, XIE Xiaorong, MU Gang. WAMS-based real-time prediction of transient stability for multi-machine power systems[J]. Relay, 2005, 33(7): 1-5.

[6] 高吉普, 徐长宝, 张道农, 等. 智能变电站通信网络时间性能的探讨[J]. 电力系统保护与控制, 2014, 42(16): 144-148. GAO Jipu, XU Changbao, ZHANG Daonong, et al. Time performance discussion for smart substation communication network[J]. Power System Protection and Control, 2014, 42(16): 144-148.

[7] 张新昌, 张项安. 层次化保护控制系统及其网络通信技术研究[J]. 电力系统保护与控制, 2014, 42(19): 129-133. ZHANG Xinchang, ZHANG Xiangan. Research of hierarchical protection & control system and its communication technology[J]. Power System Protection and Control, 2014, 42(19): 129-133.

[8] 孔祥玉, 赵帅, 房大中, 等. 能量函数方法在大电网追加紧急控制中的应用[J]. 电力系统及其自动化学报, 2014, 26(1): 8-12. KONG Xiangyu, ZHAO Shuai, FANG Dazhong, et al. Append emergency control strategy based on energy function method in large power system[J]. Proceedings of the CSU-EPSA, 2014, 26(1): 8-12.

[9] 汪强, 徐小兰, 葛光胜, 等. 智能变电站专用通信设备的关键技术[J]. 电力系统保护与控制, 2014, 42(7): 150-153. WANG Qiang, XU Xiaolan, GE Guangsheng, et al. Key technologies of special communication device in smart substation[J]. Power System Protection and Control, 2014, 42(7): 150-153.

[10] 李琰, 周孝信, 周京阳. 基于新增虚拟节点的系统受扰轨迹预测[J]. 电力系统自动化, 2007, 31(12): 19-22. LI Yan, ZHOU Xiaoxin, ZHOU Jingyang. The perturbed trajectories prediction based on an additional virtual node[J]. Automation of Electric Power Systems, 2007, 31(12): 19-22.

[11] 徐英, 夏世威, 毛安家, 等. 基于 WAMS 预测轨迹的IEEAC等值[J]. 电力系统保护与控制, 2010, 38(4): 31-34. XU Ying, XIA Shiwei, MAO Anjia, et al. IEEAC method based on the WAMS predicting trajectory[J]. Power System Protection and Control, 2010, 38(4): 31-34.

[12] 宋方方, 毕天姝, 杨奇逊. 基于 WAMS的电力系统受扰轨迹预测[J]. 电力系统自动化, 2006, 30(23): 27-31. SONG Fangfang, BI Tianshu, YANG Qixun. Perturbed trajectory prediction method based on WAMS[J]. Automation of Electric Power Systems, 2006, 30(23): 27-31.

[13] 李国庆, 孙福军, 任强. 基于外部观测的电力系统暂态稳定性实时预测和控制方法[J]. 电网技术, 1995, 19(1): 17-22. LI Guoqing, SUN Fujun, REN Qiang. Real-time prediction and control method for transient stability of multi-machine power system based on outside observation[J]. Power System Technology, 1995, 19(1): 17-22.

[14] 周伟, 陈允平. 自组织映射神经网络用于暂态稳定性分析的研究[J]. 电力系统自动化, 2002, 26(15): 33-38. ZHOU Wei, CHEN Yunping. Self-organizing mapping neural networks for power system transient stability assessment[J]. Automation of Electric Power Systems, 2002, 26(15): 33-38.

[15] 郑德如. 自相关与自回归预测[J]. 财经研究, 1982(6): 51-57. ZHENG Deru. Autocorrelation and autoregressive prediction[J]. Finance Research, 1982(6): 51-57.

[16] 范习辉, 张焰. 灰色自记忆模型及应用[J]. 系统工程理论与实践, 2003(8): 114-117. FAN Xihui, ZHANG Yan. A novel self-memory grey model[J]. Systems Engineering-Theory & Practice, 2003(8): 114-117.

[17] 陆君安, 夏军, 陈士华, 等. 动力系统的自记忆数值预报[J]. 数学杂志, 1998(增刊1): 11-14. LU Junan, XIA Jun, CHEN Shihua, et al. The self-memory numerical forecast for solving dynamical systems[J]. Journal of Mathematics, 1998(S1): 11-14.

(编辑 葛艳娜)

Study on prediction of generator trajectory

HU Xuekai1, LIANG Jifeng1, ZHANG Qian2, LIU Xiangyu1
(1. State Grid Hebei Electric Power Research Institute, Shijiazhuang 050021, China; 2. State Grid Hebei Maintenance Branch, Shijiazhuang 050070, China)

With the development of wide area measurement system, it is possible for power system transient instability control based on real-time trajectory. Using real-time data to predict can take control measures as soon as possible, which can prevent out of step. Therefore, it is very important to study high-precision and long-time trajectory prediction. Proceeding from motion equations of generator, a rolling self-memory prediction method for power system is deduced. First, trigonometric function is used to fit unbalanced power; then, angular velocity is predicted by unbalanced power; at last, according to the self-memory prediction formula, power angle can be obtained. The simulation result of IEEE9 system shows that, the method mentioned in this paper can accurately predict at least 0.5s’ future trajectory. Compared with trigonometric function prediction and autoregressive prediction, this method can predict in a longer time with a higher accuracy.

power system; power angle; self-memory prediction; trigonometric function prediction; autoregressive prediction

10.7667/PSPC150580

：2015-06-03

胡雪凯(1987-)，男，硕士，工程师，主要从事电力系统计算分析工作；E-mail:719872361@qq.com

梁纪峰(1985-)，男，硕士，工程师，从事电力系统调度控制工作；

张 乾(1990-)，女，助理工程师，主要从事电气试验工作。