基于相量量测的中小型水电集群动态等值方法研究

胡柏玮，丁理杰，刘新宇，孙景涛，王晓茹，李 旻

(1.西南交通大学电气工程学院，四川 成都 610031；2.四川电力科学研究院，四川 成都 610072；3.国网四川省电力公司，四川 成都 610041)

基于相量量测的中小型水电集群动态等值方法研究

胡柏玮1，丁理杰2，刘新宇1，孙景涛1，王晓茹1，李 旻3

(1.西南交通大学电气工程学院，四川 成都 610031；2.四川电力科学研究院，四川 成都 610072；3.国网四川省电力公司，四川 成都 610041)

为了准确分析含中小型水电集群系统，针对中小型水电集群，提出了一种基于相量量测的动态等值建模方法。该方法以估计等值为基础，将扰动后互联区域间联络线上相量量测信息作为输入量，利用四阶龙格库塔法求解发电机动态方程，借助改进PSO算法实现参数的寻优更新，最终得到等值模型的各个参数。基于该方法对四川电网某地区中小型水电集群上进行动态等值建模，仿真结果证明了该方法的有效性与精确性。同时，基于仿真与负负荷表示的中小型水电集群对比分析，仿真结果证明了该方法的优越性与实用性。

中小型水电集群；动态等值；估计等值法；相量量测信息；改进PSO算法

0 引言

中小型水力发电作为一种灵活，便捷的绿色能源，在水力资源丰富的地区会大量并网。当该地区含有大量的中小型水电站，其形成的中小型水电集群将会影响系统的动态特性。在对含集中上网的中小型水电集群的系统进行分析时，建立包含每台水电机组的详细模型十分困难，不仅是因为中小型水电集群的实际参数获取困难，而且即使用典型参数表示，还是会出现潮流不收敛以及“维数灾”等情况。目前，建模时一般将其以负负荷形式表示。但该方法在仿真计算分析时会导致结果的不准确。而对中小型水电集群进行动态等值[1]，再对等值后的电网进行分析研究是精确分析的良好手段。文献[2-3]以同调等值法为基础，将小水电集群等值为 3阶发电机模型并联负荷的形式，并分析了其对主网稳定性影响。文献[4]将4阶发电机模型并联负荷模型作为等值模型，利用同调等值对小水电集群进行动态等值。但是，传统的同调等值法在对水电集群进行等值时需知该集群的结构与参数，具有很大的局限性[5-6]。文献[7]利用估计等值法仅将河北电网某一电厂等值为一台3阶发电机，但并未对某区域进行等值；文献[8-9]把 IEEE39节点某一区域以及天津电网外网均等值为一台6阶发电机，但并未对参数可辨识性进行分析，且未提出针对水电集群的等值模型与方法。文献[10-11]通过调用PSASP暂态稳定计算模块获得某组等值参数下变电站出口的功率响应，分别将3台水电机与8台水电机均等值为一台3阶发电机，但该方法须结合研究系统模型，且等值系统太小，不具有实际意义。因此，针对中小型水电集群结构与参数未知的情况下，仅仅依靠相量量测信息的估计等值方法研究具有十分重要的意义。

本文针对结构与参数未知的中小型水电集群，结合其特点，提出一种以估计等值为基础的动态等值模型与方法。该方法仅须将扰动后互联区域间联络线上相量量测信息作为输入，利用四阶龙格库塔法求解发电机动态方程，借助改进PSO算法实现等值模型参数的寻优更新，即可得到把集中上网的中小型水电集群等值为单一发电机并联恒功率负荷模型的各参数。应用该方法对含中小型水电集群的实际电力系统进行等值建模，仿真结果表明采用该方法建立的等值模型精度可满足系统暂态稳定分析的要求；与负负荷表示的水电集群对比分析，结果表明本文所提方法能精确含中小型水电集群电网的分析结果。

1 水电集群动态等值模型

中小型水电集群一般通过220 kV及以下电压等级的变电站上网，再通过500 kV变电站接入主网。所要等值的水电集群通过联络线与内部系统连接，而等值区域中各水电机组电气距离较近，在内部系统发生扰动时，外部系统中所包含的水电集群可以认为全部同调[12]。基于上述特点，本文采用的中小型水电集群动态等值模型如图1所示，为单一发电机并联单一负荷的形式。

图1 动态等值模型结构图Fig. 1 Dynamic equivalent model structure

1.1 等值发电机模型

进行机电暂态计算时，由于二阶发电机模型不计阻尼绕组与励磁绕组的动态过程，因此只能反映原系统的稳定趋势，与原系统的动态特性差异较大；文献[13]基于仿真对比分析了发电机动态等值模型对动态等值性能的影响，结果表明五阶以上发电机模型相对于三阶模型寻优耗时大大增加但等值精度并未明显提高。本文等值发电机采用计及励磁绕组与阻尼绕组动态过程的常用三阶机电暂态模型[14]，励磁系统采用比例反馈模型，调速系统采用转矩恒定模型，其模型方程如式(1)所示。

式中：Tj为惯性时间常数；Pm为机械功率；E¢为dx¢后的电动势，代替了q轴暂态电动势qE¢；V为机端电压；dx¢为d轴暂态电抗，其值与q轴同步电抗xq相等(忽略暂态凸极效应)；d为Eq与端电压的夹角；D为阻尼系数；t为时间；w为转子转速；wf为参考轴转速；0dT¢为d轴暂态开路时间常数；Ef0为初始励磁电压；Kv为励磁电压反馈系数；V0为初始机端电压；xd为d轴同步电抗。

1.2 等值负荷模型

由于等值负荷对于系统动态特性影响较小[4]，因此等值负荷模型采用恒功率模型，即负荷有功功率与无功功率均为一个定值。文献[12]已对等值模型为3阶发电机并联静态负荷模型进行了可辨识性分析，理论证明了模型参数的可辨识性。由前述分析，可得到联络线功率方程为

式中：Pl、Ql分别为联络线功率；Pe、Qe分别为发电机输出功率；Ps、Qs分别为负荷有功与无功功率。

2 水电集群等值方法

2.1 水电集群等值框架

同步相量测量技术已广泛应用于电力系统动态监控中。基于参数辨识的估计等值法利用系统扰动后互联区域间联络线上的动态信息通过辨识算法来获取等值模型参数[15-18]。本文通过提取扰动时实际系统联络线上量测信息作为输入，辨识出等值模型参数，即a=[Tj、xd、dx¢、0dT¢、Kv、D、Ps、Qs]。其总体框架如图2所示。

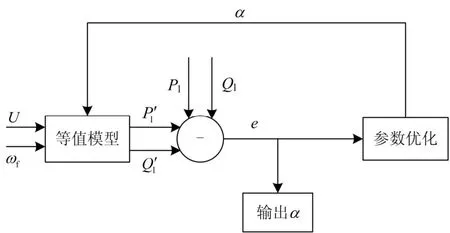
图2 水电集群等值框架图Fig. 2 Equivalent schematic diagram of hydropower generator group

该过程首先须初始化一套待辨识参数a，将扰动时联络线上电压与频率响应作为输入，求解等值模型方程，获得该套辨识参数下联络线上有功和无功功率lP¢和lQ¢。对比有功与无功功率的计算值与量测值，产生误差 e，若误差大于设定阈值，则利用优化算法更新待辨识参数a，重复上述过程；否则输出a作为等值模型参数。误差根据欧式距离求得，计算公式如(3)所示。

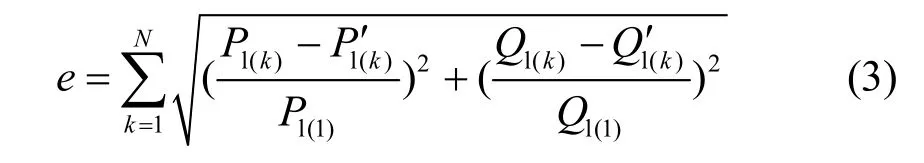
其中，N为采样点总数。

本文采用四阶龙格库塔法求解发电机动态方程，获取等值模型下联络线上的有功与无功功率。该框架如图3所示。

图3 联络线功率获取框架图Fig. 3 Schematic diagram of power on interconnection line

该过程以发电机内部变量w、d、E’作为状态变量，由发电机动态方程，结合4阶龙格库塔法，就可根据k时刻的状态变量求得k+1时刻的状态变量，进而根据发电机功率方程获得输出功率，最终得到该套等值模型参数下联络线功率。其状态变量的初值可以根据稳态相量图求得。各时刻状态变量迭代如式(4)所示。

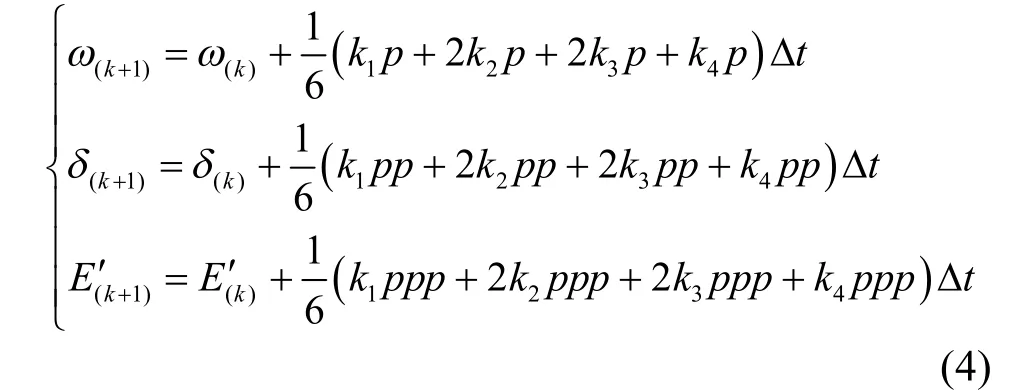
其中，k1p-k4ppp为各时刻迭代系数，由发电机动态方程变换获得。由于篇幅原因，这里不给出其计算公式。

发电机在机端电压和频率信号激励下各个时刻的电功率输出响应为

2.2 改进PSO算法在估计等值中的应用

粒子群优化(PSO)算法设置参数少、易于操作、全局收敛性好、搜索效率高等特点在电力系统优化问题上得到广泛应用[19-25]。本文结合前人对基本PSO算法进行的改进，进一步优化改进的 PSO算法。利用该方法对等值模型进行参数辨识。

基本PSO算法须初始化一群随机粒子，然后通过迭代寻找最优解。在每一次的迭代过程中，粒子通过跟踪两个“极值”来更新自己：一个是粒子本身所找到的最优解(个体极值pbest)，另一个是整个种群目前找到的最优解(群体极值gbest)。每个粒子按下式分别更新自己的速度和位置。

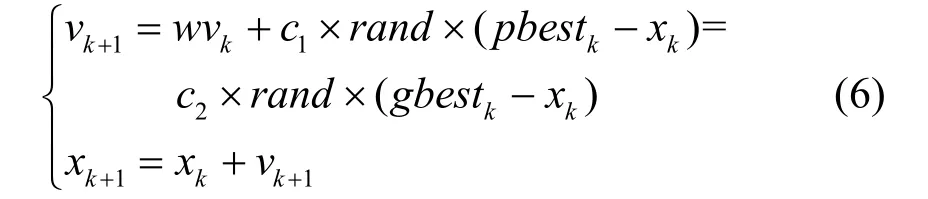
式中：vk为粒子的速度向量；w是惯性权重因子，一般取0.5~0.8的某一常数；c1和c2为学习因子，一般取2；rand为0至1之间的随机数，xk为粒子的位置向量。种群规模一般取30-50。

为平衡全局搜索和局部搜索能力，提高陷入局部最优后的自救能力，增强全局最优解的搜索能力，对基本PSO算法进行如下两条改进：

(1) 已有学者对惯性权重因子按线性递减的方式进行调整，公式如下：

式中：wmax和wmin分别为惯性权重的上下限，分别设为0.9和0.4；k为当前迭代次数；kmax为最大迭代次数。在搜索前期w较大，有利于全局搜索；在搜索后期w较小，有利于局部开发。

(2) 本文提出粒子变异策略。当群体极值 gbest的目标函数值稳定次数达到某一阈值且离最大迭代次数还有一定距离时，随机产生当前粒子的速度和位置，使其尽可能跳出局部最优，更好的搜寻全局。

基于改进 PSO算法求解上述动态等值模型参数的流程如图4所示。

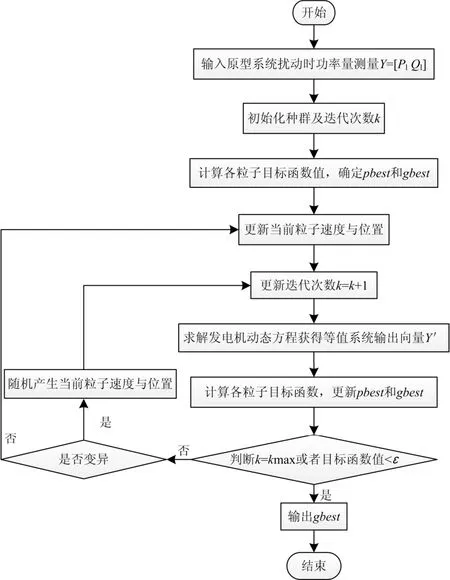
图4 基于改进PSO算法的参数辨识流程图Fig. 4 Flow chart of parameter identification based on modified PSO algorithm

具体步骤为：

(1) 输入原型系统扰动时互联区域间联络线上的有功功率Pl和无功功率Ql。

(2) 初始化各个粒子的待辨识参数a及迭代次数。

(3) 计算各粒子对应的目标函数值，确定初始的pbest和gbest。

(4) 更新当前粒子速度与位置。

(5) 更新迭代次数。

(6) 求解发电机动态方程，获得该等值模型参数下的联络线上的有功功率和无功功率。

(7) 计算各粒子的目标函数值，并更新pbest与gbest。

(8) 判断是否满足终止条件，若满足则终止，输出gbest；否则判断是否需要变异，若需要则随机产生当前粒子速度和位置并返回(6)；否则返回(5)更新各个粒子的速度和位置，继续循环计算。

3 仿真验证

3.1 可辨识性验证

在四川电网设置某500 kV线路N-1故障，将联络线响应作为量测数据，采用本文所述的方法对发电机及负荷进行参数辨识，得到的结果和实际模型参数比较如表1所示，辨识得到的响应曲线与实际响应曲线如图5、图6所示。

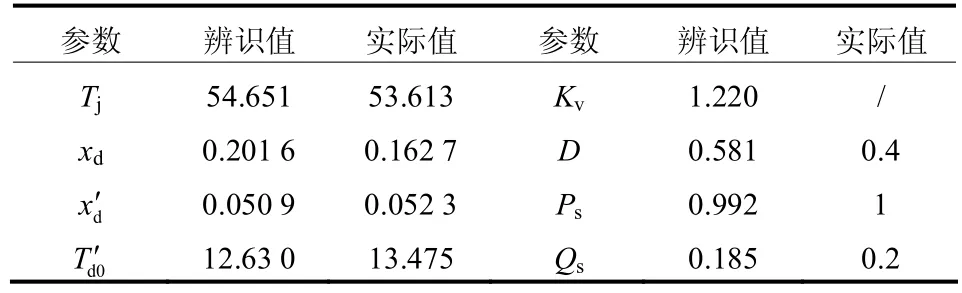
表1 模型辨识参数和实际参数比较(标幺值)Table 1 Comparison of the identified parameters and the real parameters of the model (p.u.)

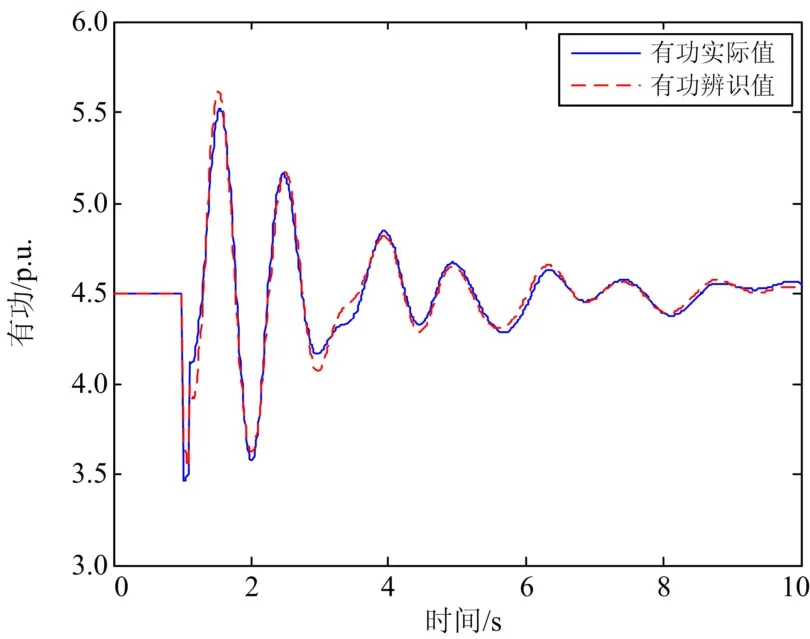
图5 辨识值与实际值有功功率响应曲线Fig. 5 Active power curves based on identified parameters and real parameters

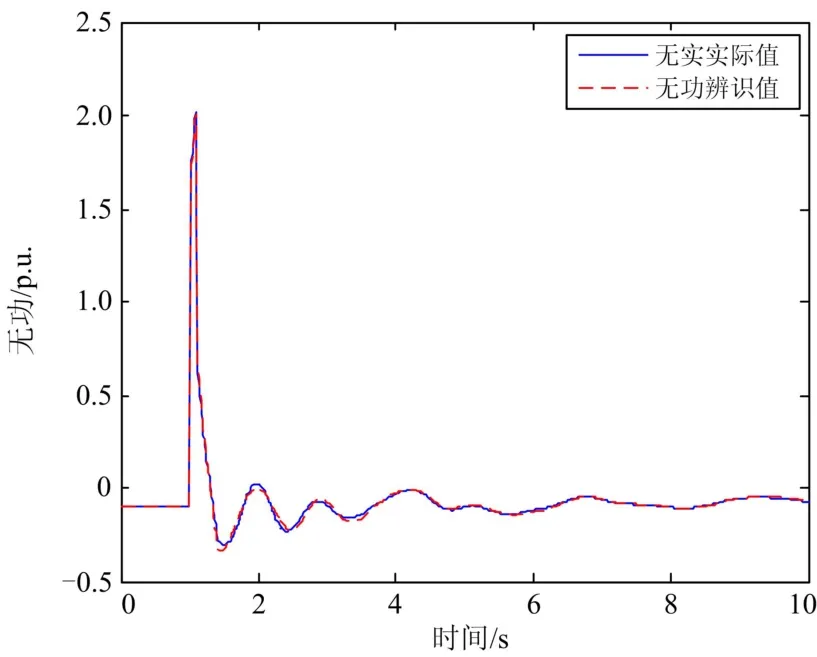
图6 辨识值与实际值无功功率响应曲线Fig. 6 Reactive power curves based on identified parameters and real parameters

由表1可知，辨识得到的参数与实际模型参数十分接近，说明这些参数是可辨识的。由于该方法侧重于全局寻优，且引入了Kv表示的简化励磁系统模型，使得某些参数偏离实际值，但并不影响整个动态过程的精度。从图5、图6可见，辨识得到的响应曲线与实际响应曲线具有很高的拟合度，误差很小，说明本文提出的改进粒子群算法鲁棒性好，寻优能力强。

3.2 水电集群动态等值

四川作为水电能源丰富地区，其水电装机容量占总装机容量的60%以上。四川某地区分布了近10座水电站，水电机组共计23台，总容量达1 548 MW。以该地区500 kV水电送出通道为例，对比分析以负负荷表示的水电集群与实际水电集群的动态响应特性，其中，负负荷分别采用40%电动机+60%恒阻抗负荷与考虑压变与频变的静态负荷模型。图7、图8为扰动后上述三种不同模型的功率响应曲线对比图。扰动为某500 kV线路发生N-1故障。

图7 不同模型有功功率响应曲线Fig. 7 Active power curves based on different models

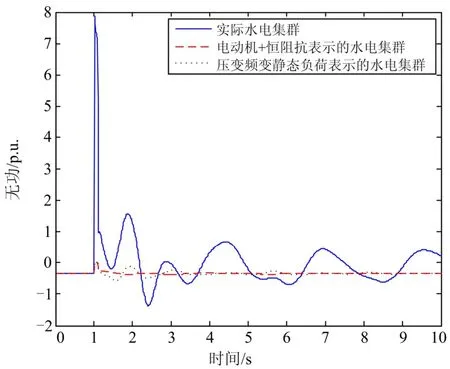
图8 不同模型无功功率响应曲线Fig. 8 Reactive power curves based on different models

由图7、图8可见，以负负荷表示的水电集群并不能准确描述实际水电集群的动态响应特性，这是由发电机与负荷模型的本质差别所决定的。因此，对中小型水电集群进行动态等值是精确分析的良好手段。

为分析该区域的中小型水电集群对四川主网动态特性的影响，采用本文提出的估计等值方法对该区域中小型水电集群进行动态等值建模，扰动为相同500 kV线路发生N-1故障。等值模型参数如表2所示。系统等值前后的功率响应曲线如图9、图10所示。

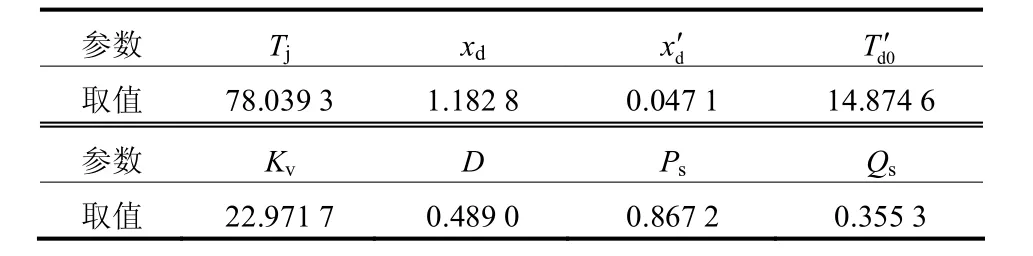
表2 等值模型参数(标幺值)Table 2 Parameters of equivalent model (p.u.)

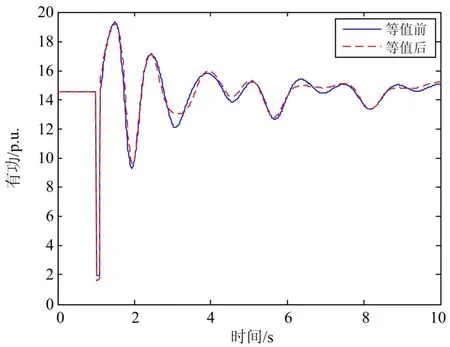
图9 等值前后联络线有功功率响应曲线Fig. 9 Active power curves of original and equivalent model

图10 等值前后联络线无功功率响应曲线Fig. 10 Reactive power curves of original and equivalent model

由上图可知，等值前后联络线上有功与无功响应曲线不仅总体动态响应趋势一致，还具有较高的拟合度，满足等值要求。

综上所述，本文所提出的基于改进PSO算法的中小型水电集群估计等值方法不仅快速简单，还准确实用，仅仅依赖量测信息就可对中小型水电集群进行动态等值，改善了目前由负负荷表示的水电集群的仿真计算精度低的不足，具备一定的工程实用价值。

4 结论

在对含中小型水电集群的电网进行动态特性分析时，负负荷表示的水电集群无法满足计算精度要求，而传统的同调等值法具有很大的局限性。针对上述实际问题，本文以估计等值法为基础，提出了一种基于相量量测的水电集群等值及参数辨识的方法。该方法利用四阶龙格库塔法求解发电机动态方程，借助改进 PSO算法实现各个参数的更新寻优，最终辨识出等值模型中的各个参数。采用所提出的方法对四川电网某区域的中小型水电集群进行等值建模，仿真结果验证了该方法的有效性与优越性，为计及中小型水电集群的电网分析奠定了基础。

[1] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.

[2] LIU Y, LI X, WANG Y, et al. Research on small signal stability of power system with distributed small hydropower[C] // Innovative Smart Grid Technologies-Asia, IEEE. IEEE, 2012: 1-6.

[3] 张元胜. 分布式小水电对电力系统运行稳定性影响的研究[D]. 长沙: 湖南大学, 2012. ZHANG Yuansheng. The effects on stable running of power grid of the distributed network with small hydropower[D]. Changsha: Hunan University, 2012.

[4] 王敏, 文劲宇, 胡文博, 等. 区域小水电机群动态等值建模方法研究[J]. 电力系统保护与控制, 2013, 41(17): 1-9. WANG Min, WEN Jinyu, HU Wenbo, et al. A dynamic equivalent modeling for regional small hydropower generator group[J]. Power System Protection and Control, 2013, 41(17): 1-9.

[5] 鞠平, 王卫华, 谢宏杰, 等. 3区域互联电力系统动态等值的辨识方法[J]. 中国电机工程学报, 2007, 27(13): 29-34. JU Ping, WANG Weihua, XIE Hongjie, et al. Identification approach to dynamic equivalents of the power system interconnected with three areas[J]. Proceedings of the CSEE, 2007, 27(13): 29-34.

[6] 刘峰. 电力系统外部等值理论及实用化探讨[J]. 继电器, 2007, 35(15): 67-71. LIU Feng. Elementary analysis of external network equivalence[J]. Relay, 2007, 35(15): 67-71.

[7] 张宁. 基于相量测量的同步发电机参数辨识研究[D].北京: 华北电力大学, 2007. ZHANG Ning. Research on the identification of synchronous generator parameters based on phasor measurement[D]. Beijing: North China Electric Power University, 2007.

[8] 杨靖萍. 大规模互联电力系统动态等值方法研究[D].杭州: 浙江大学, 2007. YANG Jingping. Study on dynamic equivalents methods for large-scale power systems[D]. Hangzhou: Zhejiang University, 2007.

[9] 李晓辉, 罗敏, 刘丽霞, 等. 动态等值新方法及其在天津电网中的应用[J]. 电力系统保护与控制, 2010, 38(3): 61-66. LI Xiaohui, LUO Min, LIU Lixia, et al. A new dynamic equivalence method and its application in Tianjin Grid[J]. Power System Protection and Control, 2010, 38(3): 61-66.

[10] 魏巍, 丁理杰, 史华勃, 等. 基于变电站线路出口信息的小水电群等值及参数辨识研究[J]. 四川电力技术, 2013, 36(5): 20-24. WEI Wei, DING Lijie, SHI Huabo, et al. Equivalence and parameter identification for small hydropower generator groups based on information of substation line[J]. Sichuan Electric Power Technology, 2013, 36(5): 20-24.

[11] SHI H B, HU B W, SUN J T. Research on hydropower generator group equivalence and parameter identification based on PSASP calling and optimization algorithm[C] // 2014 International Conference on Power and Energy, November 29-30, 2014, Shanghai, China.

[12] 鞠平. 电力系统建模理论与方法[M]. 北京: 科学出版社, 2010.

[13] 杨琴, 管霖, 王同文. 等值机模型的选择对动态等值性能的影响研究[C] // 中国高等学校电力系统及其自动化专业第二十四届学术年会论文集, 北京, 2008. YANG Qin, GUAN Lin, WANG Tongwen. Influence on the performance of dynamic equivalence based on equivalent model[C] // The 24th Annual Conference Proceedings about Power System and Automation in China. Beijing, 2008.

[14] 周杨. 互联电力系统区域动态等值方法研究[D]. 武汉:华中科技大学, 2012. ZHOU Yang. Research on dynamic equivalent method for interconnected power system areas[D]. Wuhan: Huazhong University of Science and Technology, 2012.

[15] PRICE W W, EWART D N, GULACHENSKI E M, et al. Dynamic equivalents from on-line measurements[J]. IEEE Transactions on Power Apparatus & Systems, 1975, 94(4): 1349-1357.

[16] 周云海, 李咸善, 胡翔勇, 等. 基于联络线动态潮流的动态等值方法[J]. 电工电能新技术, 1999, 11(5): 29-33. ZHOU Yunhai, LI Xianshan, HU Xiangyong, et al. Dynamic equivalents based on the transient power flow of the connecting lines[J]. Advanced Technology of Electrical Engineering and Energy, 1999, 11(5): 29-33.

[17] JU P, NI L Q, WU F. Dynamic equivalents of power systems with online measurements, part 1: theory[J]. IEE Proceedings-Generation, Transmission and Distribution, 2004, 151(2): 175-178.

[18] 张元, 郝丽丽, 戴嘉祺. 风电场等值建模研究综述[J].电力系统保护与控制, 2015, 43(6): 138-146. ZHANG Yuan, HAO Lili, DAI Jiaqi. Overview of the equivalent model research for wind farms[J]. Power System Protection and Control, 2015, 43(6): 138-146.

[19] 韩美玉, 王艳松, 张丽霞. 基于粒子群算法的电力系统非线性谐波状态估计[J]. 电力系统保护与控制, 2013, 41(22): 98-102. HAN Meiyu, WANG Yansong, ZHANG Lixia. Research on non-linear harmonic state estimation in power system based on particle swarm optimization algorithm[J]. Power System Protection and Control, 2013, 41(22): 98-102.

[20] 马建伟, 陈珊珊. 线性递减权重粒子群优化人工神经网络算法的光伏系统谐波检测[J]. 低压电器, 2014(4): 60-68. MA Jianwei, CHEN Shanshan. Harmonic detection of linear decreasing weight particle swarm optimization artificial neural network algorithm in photovaltaic system[J]. Low Voltage Apparatus, 2014(4): 60-68.

[21] 胡卫利, 程亮, 马倩, 等. 基于改进粒子群组合算法的电网基建年度投资预测[J]. 电网与清洁能源, 2014, 30(11): 52-64. HU Weili, CHENG Liang, MA Qian, et al. Prediction of annual power grid infrastructure investment based on hybrid algorithm of improved PSO[J]. Power System and Clean Energy, 2014, 30(11): 52-64.

[22] 周晖, 付娅, 韩盟, 等. 基于粒子群算法的含大规模风电互联系统的负荷频率控制[J]. 电力系统保护与控制, 2014, 42(10): 1-7. ZHOU Hui, FU Ya, HAN Meng, et al. Load frequency control of power systems with large scale of wind power integrated based on particle swarm algorithm[J]. Power System Protection and Control, 2014, 42(10): 1-7.

[23] 姜志鹏, 文习山, 蓝磊, 等. 粒子群算法应用于避雷器均压环配置优化[J]. 高压电器, 2014, 50(1): 102-106. JIANG Zhipeng, WEN Xishan, LAN Lei, et al. Application of particle swarm optimization algorithm to configuration optimization of grading rings for arrester[J]. High Voltage Apparatus, 2014, 50(1): 102-106.

[24] 卢旻, 吴绍武, 谢剑锋. 基于迁徙型 PSO算法的风光储系统配置优化分析[J]. 电器与能效管理技术, 2015(14): 33-46. LU Min, WU Shaowu, XIE Jianfeng. Configuration optimization of wind-solar storage system using MPSO algorithm[J]. Electrical & Energy Management Technology, 2015(14): 33-46.

[25] 刘欢, 刘志刚. 基于改进粒子群算法的牵引变电所维修优化研究[J]. 电力系统保护与控制, 2015, 43(11): 87-94. LIU Huan, LIU Zhigang. An improved particle swarm algorithm study on optimization model of maintenance schedules for railway traction substations[J]. Power System Protection and Control, 2015, 43(11): 87-94.

(编辑 张爱琴)

A dynamic equivalent method for centralized small and medium hydropower generator group based on phasor measurement information

HU Bowei1, DING Lijie2, LIU Xinyu1, SUN Jingtao1, WANG Xiaoru1, LI Min3
(1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Sichuan Electric Power Research Institute, Chengdu 610072, China; 3. Sichuan Power Corporation of State Grid, Chengdu 610041, China)

To analyze power system with centralized small and medium hydropower generator group accurately, this paper proposes a method to build a dynamic equivalent model of small and medium hydropower generator group based on phasor measurement information. Some procedures, such as inputting the phasor measurement information which exists in interconnection line after a disturbance, solving the generator dynamic equations based on 4-order Runge-Kutta method, and using modified PSO algorithm to update each parameter, are used in this method based on estimate equivalent method. For validation purposes, the proposed method is applied to the centralized small and medium hydropower generator group in Sichuan province. Results show that the reduced system retains the dynamic performance of the original system with good accuracy. Further simulations are made to compare with small and medium hydropower generator group which represent as a negative load. Results prove the superiority and practicability of the dynamic equivalent method.

centralized small and medium hydropower generator group; dynamic equivalent; estimate equivalent method; phasor measurement information; modified PSO algorithm

10.7667/PSPC151081

：2015-07-16

胡柏玮(1990-)，男，硕士研究生，研究方向为电力系统安全稳定分析；E-mail: 409134117@qq.com

丁理杰(1981-)，男，博士，高级工程师，研究方向为电力系统规划、运行以及稳定性研究；

刘新宇(1990-)，男，硕士研究生，研究方向为电力系统动态监测。