基于小波变换和改进Prony方法的电能质量扰动分析

任子晖，刘昊岳，徐进霞

(中国矿业大学信息与电气工程学院，江苏 徐州221008)

基于小波变换和改进Prony方法的电能质量扰动分析

任子晖，刘昊岳，徐进霞

(中国矿业大学信息与电气工程学院，江苏 徐州221008)

传统的电能质量分析方法通常只针对某一类特定的电能质量扰动问题进行分析，为了实现对常见电能扰动信号进行有效的区分与辨识，提出小波分析与 Prony方法相结合的分析算法。首先引入小波多分辨分析(multi-resolution analysis)，选取合适的小波函数对扰动信号进行分解，判断分解信号是否存在模极大值点，从而区分出稳态与暂态电能质量扰动问题。对于暂态扰动问题，优化了Mallat重构层数，提取出暂态扰动波形，以实现对扰动类型的判断。对于稳态扰动问题，改进Prony方法对于系统阶数估计的过程，提高了参数辨识精度。最后对混合扰动信号进行分析，并使用Matlab进行了仿真和实验验证。仿真和实验结果表明，该算法能准确地识别出各种类型的电能质量扰动信号。

电能质量；小波分析；Mallat重构；Prony方法；参数辨识

0 引言

随着国家的发展，我国电力工业的规模迅速扩大，用电负荷急剧增长，其中一些非线性负荷与冲击负荷严重影响了电力系统的供电质量，给用户带来了很大的困扰，有必要对扰动信号进行有效的分析与抑制[1-2]。目前常用的电能质量分析方法包括快速傅里叶变换法(FFT)[3]、小波变化法[4]、S变换法[5]、基于形态学的方法[6]等。这些算法往往只针对特定的某种电能质量问题进行分析，对于多个含噪声的常见扰动信号并不具备通用的分析方法。

针对以上问题，本文提出使用小波多分辨率分析与改进的Prony方法结合起来实现对常见电能质量问题进行辨识的算法。首先选取合适的小波函数对扰动信号进行多分辨率分析，通过对第一层高频系数的对比区分出暂态电能质量问题与稳态电能质量问题，如是暂态扰动，则使用优化层数的小波重构算法对信号进行重构，并提取出暂态波形，对其进行分析便可得出暂态扰动类型。如是稳态扰动，则使用Prony方法对信号进行拟合，得到扰动信号的特征参数。由于经典的Prony方法在噪声抑制、非平稳信号的拟合能力以及系统阶数的估计等方面效果并不理想，本文对经典Prony方法进行改进，使其能满足复杂电能信号的辨识精度。最终提出一套基于小波变换和改进Prony方法对常见扰动信号进行辨识的算法。

1 基于小波变换的电能质量扰动识别

1.1 小波多分辨分析

多分辨分析(multiresolution analysis)是可以将信号在一系列相异的空间上进行分解的方法，它的基本思想是在的某个子空间里确定基底，然后利用平移与伸缩变换，将子空间的基底扩展到里。

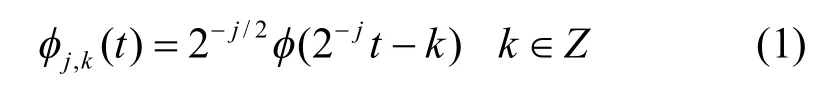
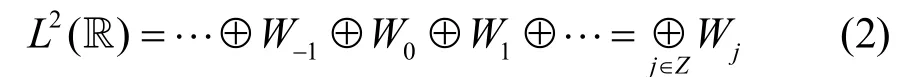
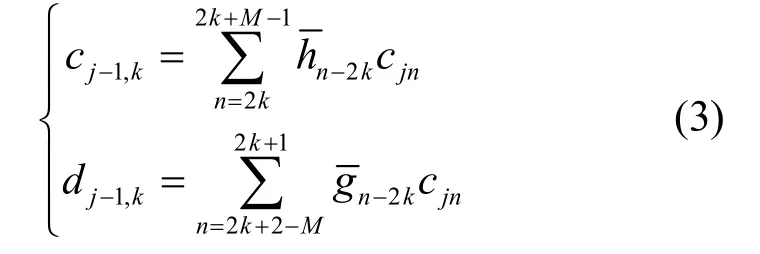
重构公式为

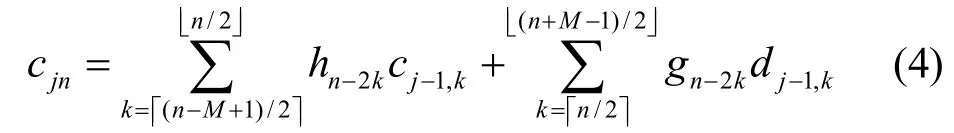
1.2 暂态电能质量扰动的检测

在对电能质量扰动的检测中，利用小波分析可以探测信号中暂态反常的部分，选取最优的小波基可提高信号辨识的精度。Daubechies小波具有正交性及紧支撑性，对于信号突变点的检测有较好的灵敏度，是理想的小波函数。文献证明了小波最适宜应用在暂态电能质量扰动识别中。

选取合适的小波函数之后，还需确定相应的分解层数。实际应用中一般使用公式来计算频带的划分数目，为分解的层数，式中为系统的基频，为采样频率。而后进行模极大值的判定。首先对第一、二层高频系数进行求模平均，结果记为再得到其极大模记为若大于某阈值(由文献知在实际应用中一般取则可认为检测到暂态波动。

在实际电网中，多种电能质量问题可能会同时出现，而稳态电能质量扰动可能会对暂态扰动的检测产生不利影响，为了验证在复杂环境中上述小波算法的准确度，不失一般性地，构造混有3次、20次谐波以及2.5次间谐波干扰信号的电能质量暂态扰动模型：

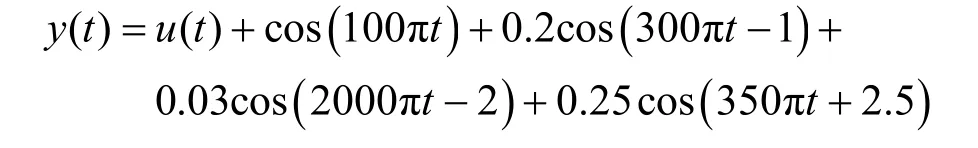
图1为加入噪声后模型的原始波形以及经db4小波 6层分解后的 d1层离散细节。实验得 d1层mean=0.000665，max分别出现在第261及288个点上，其值分别为0.026 1及0.031 5，可得两个点的M值为38.25和46.37，可判定检测到信号突变点。可见该算法即使在含有谐波、噪声等干扰的情况下依然能很好地检测出是否发生电能质量暂态扰动。

图1 原始信号及d1层小波分解Fig. 1 Original signal and d1 layer wavelet decomposition

1.3暂 态扰动波形的提取

为了对扰动信号进行进一步分类分析，需要提取并存储电能质量扰动的波形。由于小波分解算法会将信号分解到不同的子频带，电网中的干扰信号会使提取的暂态波形受到影响，其中各次谐波的频谱泄漏现象对暂态扰动波形重构的精度有着较大的影响，其他干扰信号影响较小[11]。因此，需以减小谐波干扰为目的对提取方法进行改进。

考虑工频成分对d6层的干扰，先只对1~5层高频系数进行重构并相加，得到原始信号 ()yt的暂态扰动波形，如图2(a)所示。由重构波形可知，仿真结果并不理想，受到了原始信号中谐波的影响。

原信号经过小波变换后被划分为7个子频带：6.4~3.2 kHz、3.2~1.6 kHz、1.6~0.8 Hz、800~400 Hz、400~200 Hz、200~100 Hz、100~0 Hz，由于信号的谐波部分主要分布在100~200 Hz频带上，即d6层，而 d6子频带的频率成分会产生频谱泄漏，影响了d5层的重构精确度，因此在考虑谐波的影响后只对d1~d4层进行重构，重构波形如图2(b)所示。可见虽然重构波形依然受高次谐波影响，但其幅值较小，基本上消除了谐波对于暂态扰动波形提取的影响。

图2 重构波形图Fig. 2 Refactoring waveform figure

2 改进Prony方法的应用

Prony方法在谐波、电压闪变等稳态电能质量问题中有着广泛的应用，但其最大的缺点就是对噪声十分敏感，现对其进行改进并应用在稳态电能质量问题的分析中。

2.1 改进Prony方法

改进的Prony方法主要包括以下步骤：

1) 构造样本矩阵

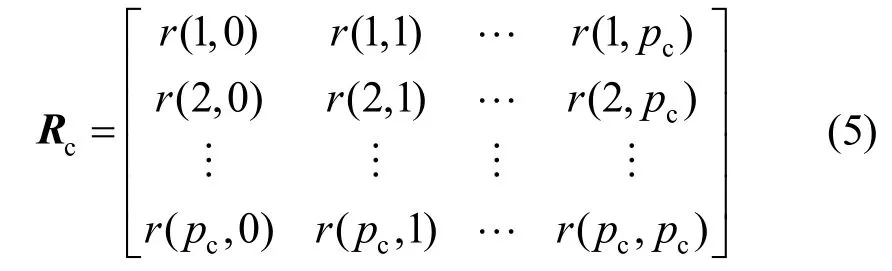
2) 系统阶数的估计

线性参数的估计可以看作求解方程组(6)的过程。

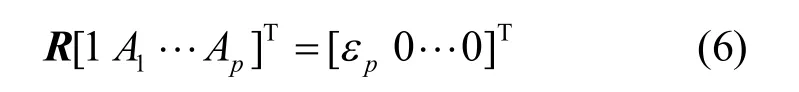
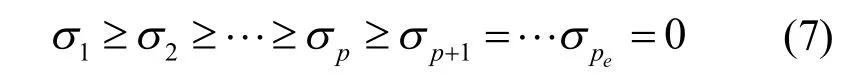
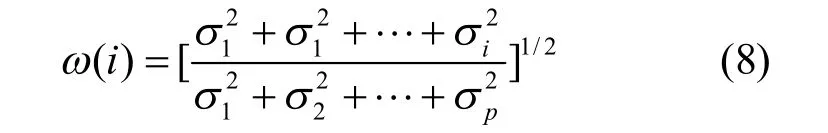
式中，p为系统的估计阶数，由于 ()iw 是单调递增的，当i值从1向p递增时，的值会向1逼近，而信号空间的奇异值明显大于噪声空间的奇异值，因此当i取到某值使得大于限值l(一般取时，可认为此时的i即为系统的实际阶数

3) 优化参数的Prony模型

将在系统实际阶数M后的噪声空间以零空间替代，即得到样本矩阵的最优近似矩阵去除噪声空间影响后，参数矩阵只有个独立参数，则可构造p + 1- M维的方程组

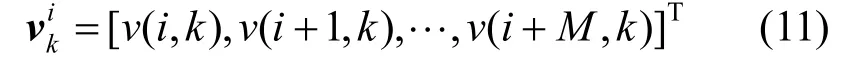
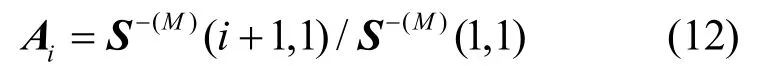
通过上述算法便能得到对原始信号的参数估计，计算出各频率分量的特征参数。

2.2 有效性测试

现将改进Prony算法应用在多种谐波混合信号的检测中进行验证，构造谐波信号：

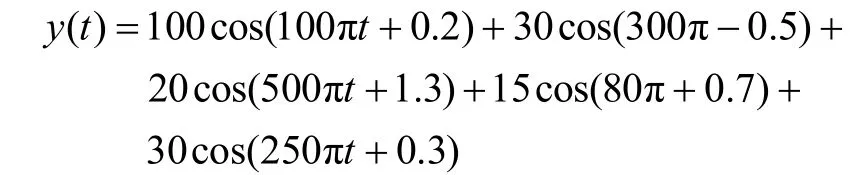
并在信号中加入信噪比为30 dB的噪声。首先使用原始Prony算法对信号进行拟合，如图3(a)所示，并与原信号作对比，得到二者的均方误差，如图3(b)。而后使用经改进的Prony方法再次拟合信号，实验结果如图3(c)与图3(d)所示，可见识别效果有了明显的改善。

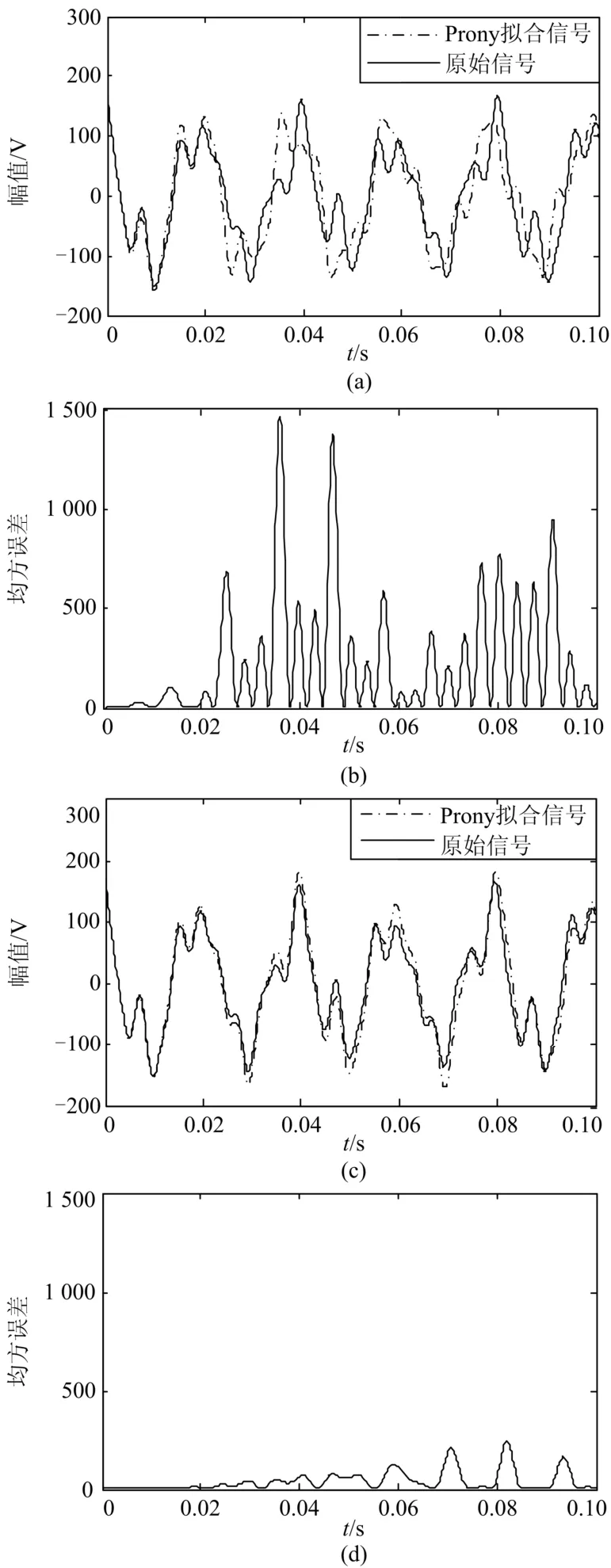
图3 Prony方法识别效果对比Fig. 3 Prony method recognition effect

为了更客观地评价算法改进前后的优劣，表 1给出了两种算法的误差对比，可见改进的Prony方法在各种误差意义上均优于传统Prony方法，且在连续波形的拟合上具有一般性。

表1 不同Prony方法的误差比较Table 1 Error comparison of different Prony method

3 算例仿真

采用Matlab在信噪比为30 dB的噪声环境下生成包括电压暂升、电压暂降、电压短时中断、振荡暂态、谐波与间谐波与电压闪变在内的六种常见的电能质量扰动信号，如图4所示，其中采样频率为10 kHz，采样长度为0.2 s，共采集2 000个数据。

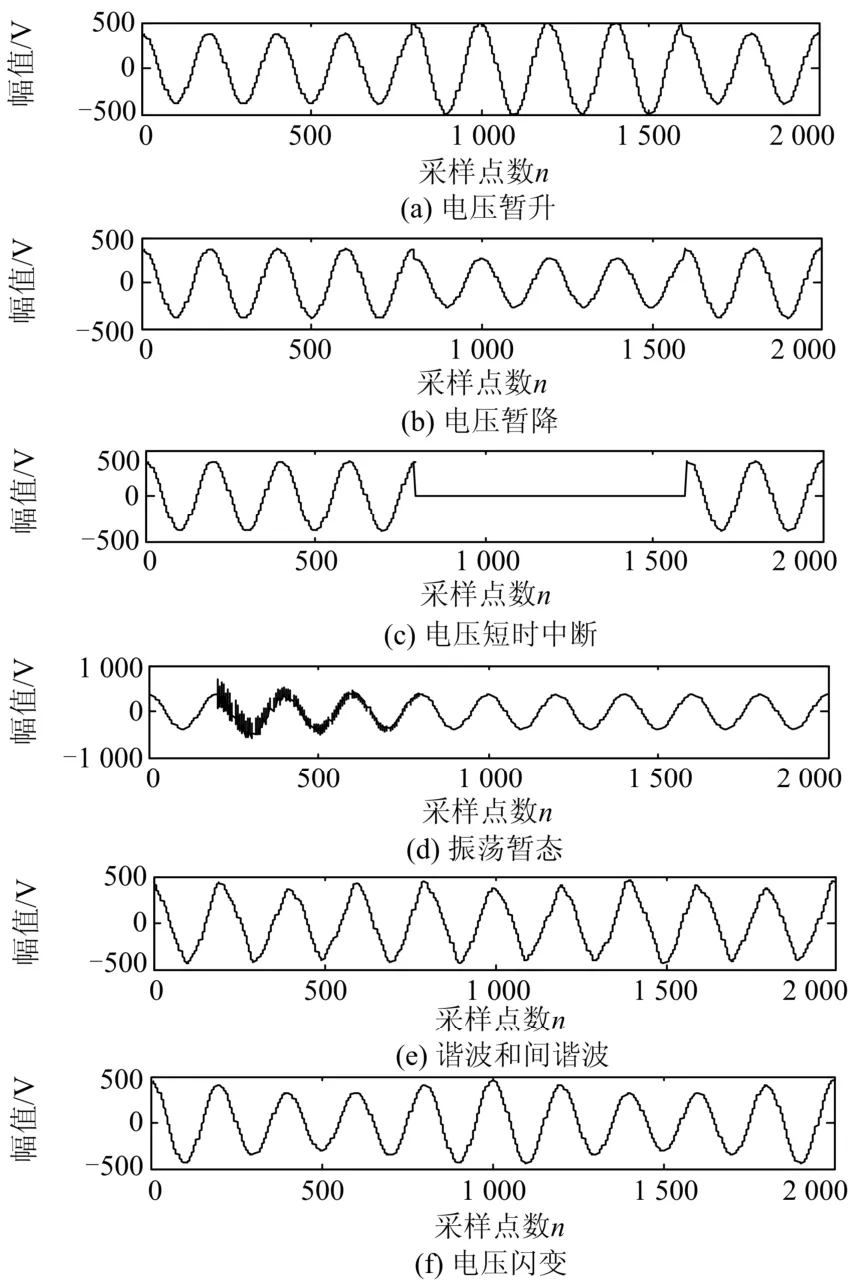
图4 6种常见的电能质量扰动信号Fig. 4 Six kinds of common power quality disturbance signal

3.1 电能质量扰动分类

根据1.2节公式可求得信号的小波分解层数为p- 1 = 6 层，对上述6种电能质量扰动信号进行db4小波的6层分解，可得出它们的d1尺度高频系数，如图5所示。

由如图5(a)~图5(c)可见，在存在噪声影响的情况下，db4小波依然能够较为准确地定位电压暂升、电压暂降与电压短时中断发生的起始与结束时刻。由图5(d)可见，暂态振荡的起始时刻有着较大的峰值，容易被定位，但其幅值呈指数递减，由于存在噪声，会对结束时刻的定位有所偏差。

由图 5(e)、图 5(f)可知，谐波与间谐波、电压闪变的高频系数很小，分布杂乱，不存在模极大值点，由此可将暂态与稳态电能质量信号有效地区分开来。

图5 信号的d1层高频系数Fig. 5 d1 layer high frequency coefficient of the signal

3.2 暂态电能质量扰动分析

由暂态扰动信号的模极大值点可确定扰动发生的起止时刻，现将实验的测量值与模型的理论计算值相对比，结果如表2所示。

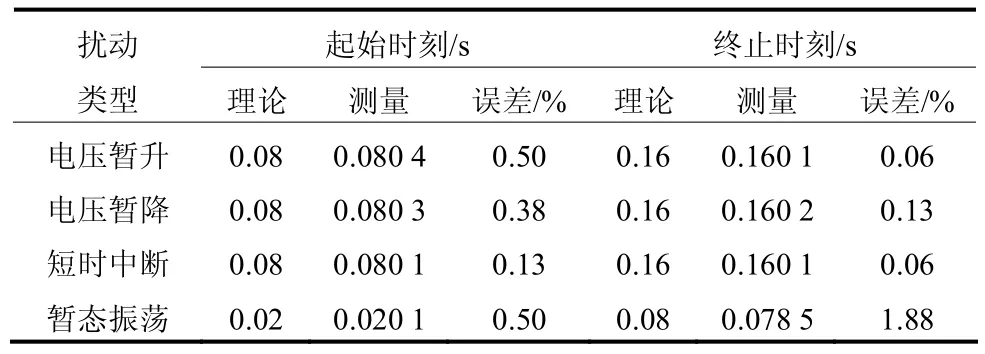
表2 扰动起止时刻检测Table 2 Detection of disturbance begin-end time

分析表2可知，在有噪声的情况下，算法较为准确地识别出电压暂升、电压暂降、电压短时中断的起止时刻，对于振荡暂态的起始时刻定位准确，而终止时刻存在一定误差，但影响不大，仍能对扰动信号进行定位。

对扰动信号进行定位后即可重构分解信号，从而提取出暂态扰动波形，提取的波形如图6所示。

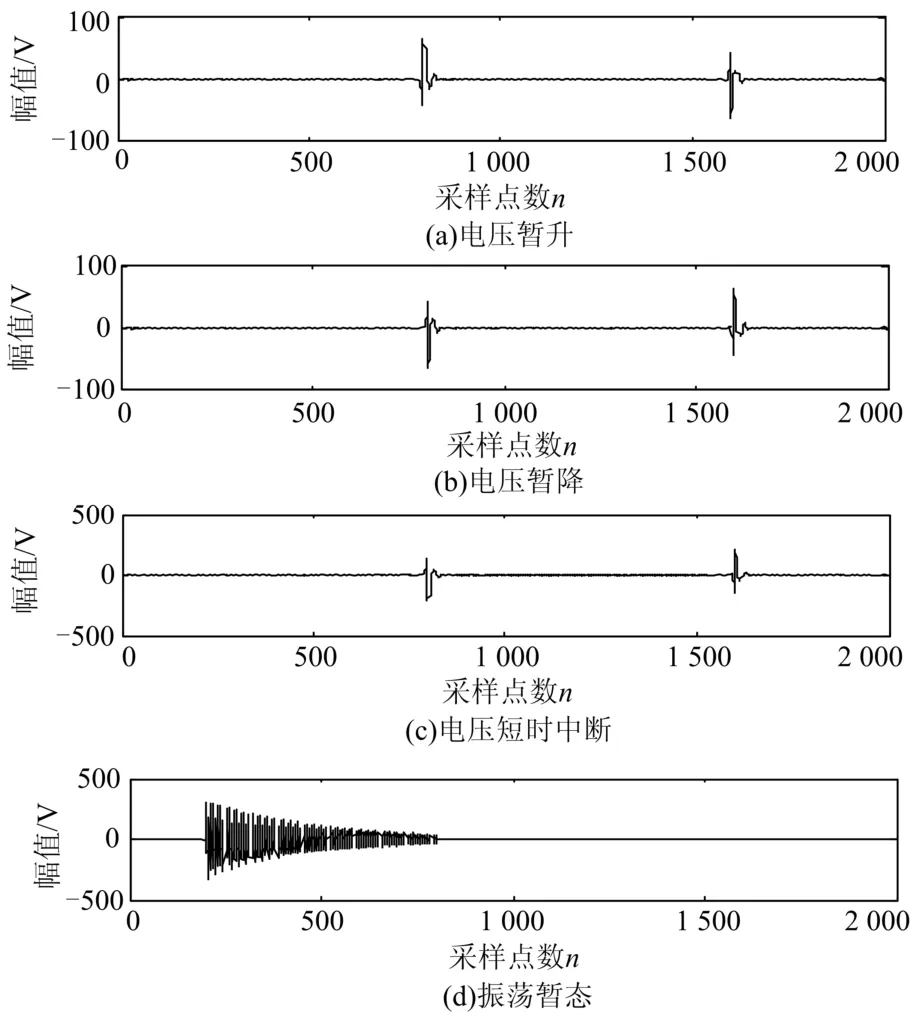
图6 暂态扰动波形提取Fig. 6 Extraction of transient disturbance waveform

由文献[12]可知，在确定扰动信号的起止位置之后，便可对原始信号序列扰动开始前后半周波的数据进行分析，使用均方根值法计算其电压有效值，便可辨识出暂态电能质量问题的类型，本文不再赘述。

3.3 稳态电能质量扰动分析

区分出稳态电能质量问题之后，采用上述改进的Prony方法对扰动信号进行分析。

图4中谐波与间谐波的混合模型为

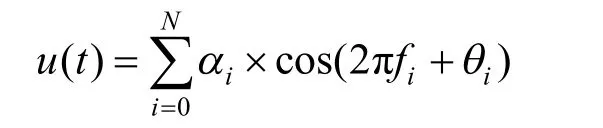
其中，N = 2 、f0= 5 0、f1= 1 50、f2= 3 5、a0= 3 80、a1= 3 0、a2= 2 0、q0= 0 、q1= 0 .5、q2= 1 .1，并含有信噪比为30 dB的高斯噪声。使用改进Prony方法拟合信号，如图7所示。表3为谐波信号的特征参数。由表3可知，采用经改进算法拟合的信号频率参数误差均在 0.01%以下，幅值误差在 2%以下，较为精确地辨识出原信号的各个分量，实现在含噪声情况下对谐波、间谐波问题的参数识别。

下面对电压闪变信号进行分析，实验中构造的是一个含噪声的单频电压闪变模型 v (t)=380 ´ [ 1 + 0 .2cos(0.2 ´ 2 π f0t) ] cos(2π f0t )，将其展开后可知该模型含有40、50、60 Hz的频率分量，对该模型进行拟合，并提取出信号的包络，所得图形如图8所示，表4为闪变信号的特征参数。由表4可知，算法对闪变信号60 Hz分量的拟合精度稍逊，但依然能够达到实际所需的水平，实现对电压闪变信号的提取与分析。

图7 谐波信号的Prony拟合Fig. 7 Prony fitting of harmonic signal

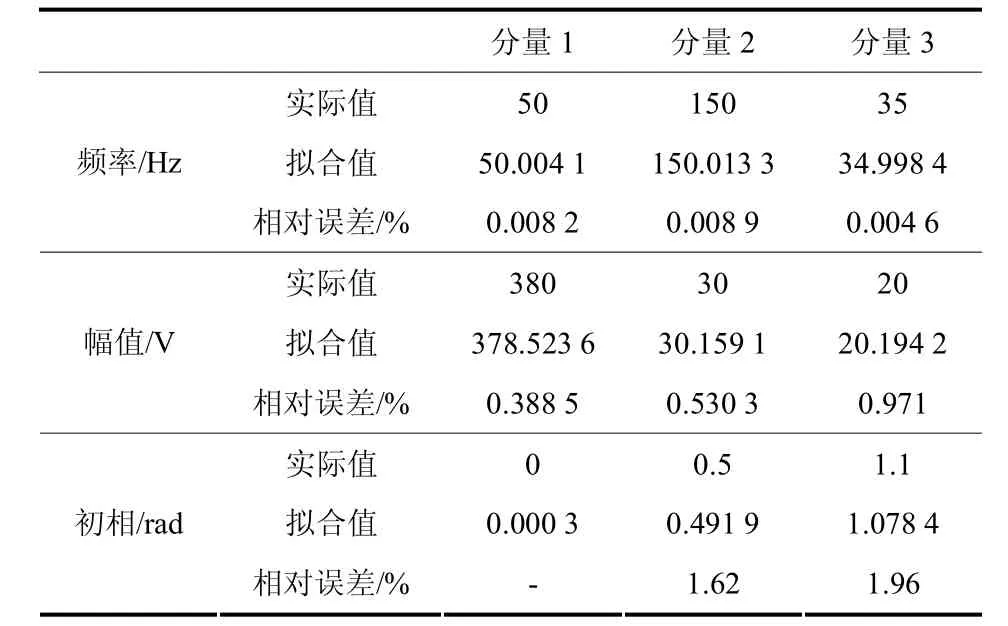
表3 谐波、间谐波信号特征参数Table 3 Signal characteristic parameters of harmonic and inter harmonic

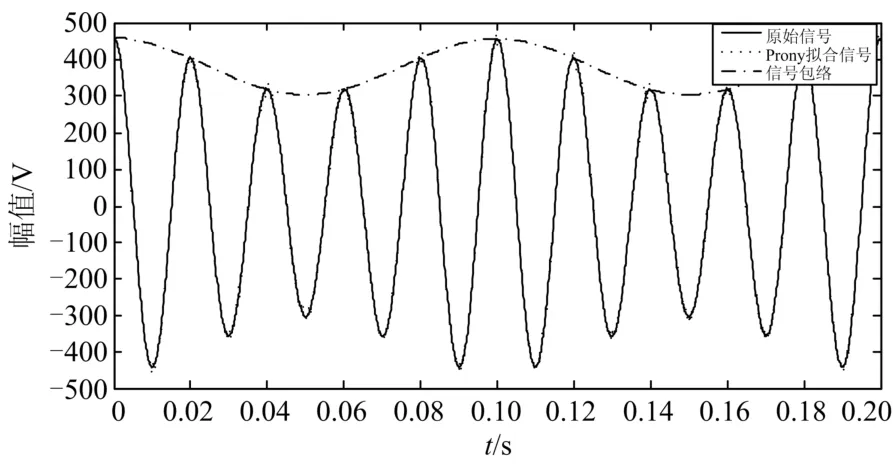
图8 闪变信号的Prony拟合Fig. 8 Prony fitting of flicker signal

3.4 混合电能质量扰动分析

在实际的电力系统中，往往存在多种电能质量问题共存的情况，对此分为两种情况进行讨论。

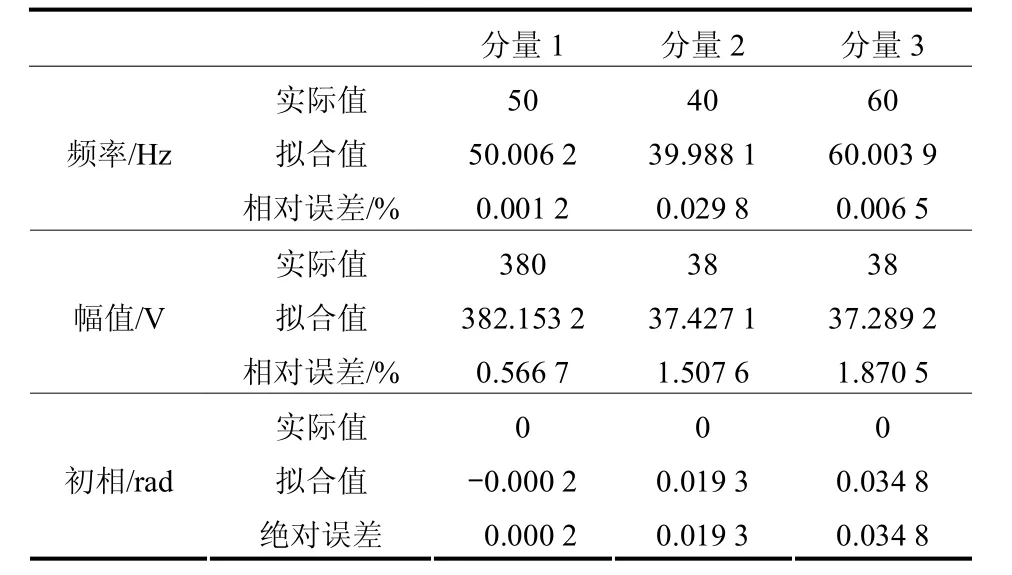
表4 电压闪变信号特征参数Table 4 Characteristic parameters of voltage flicker signal

1) 若只存在多种稳态扰动，由于所提算法在连续信号的拟合上具有一般性，可直接对混合信号进行Prony拟合，并得到所有扰动的特征参数。现构造含有3次谐波的电压闪变仿真模型：

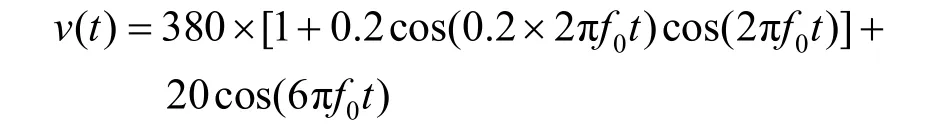
其中， f0= 5 0Hz ，并加入信噪比为 3 0 dB的高斯噪声。对模型进行改进Prony辨识得到如表5所示的特征参数。可知，算法在弱噪情况下仍然能够比较精确地分离出各频率分量，并确定各个分量的特征参数，实现对混合稳态扰动信号的识别与分析。

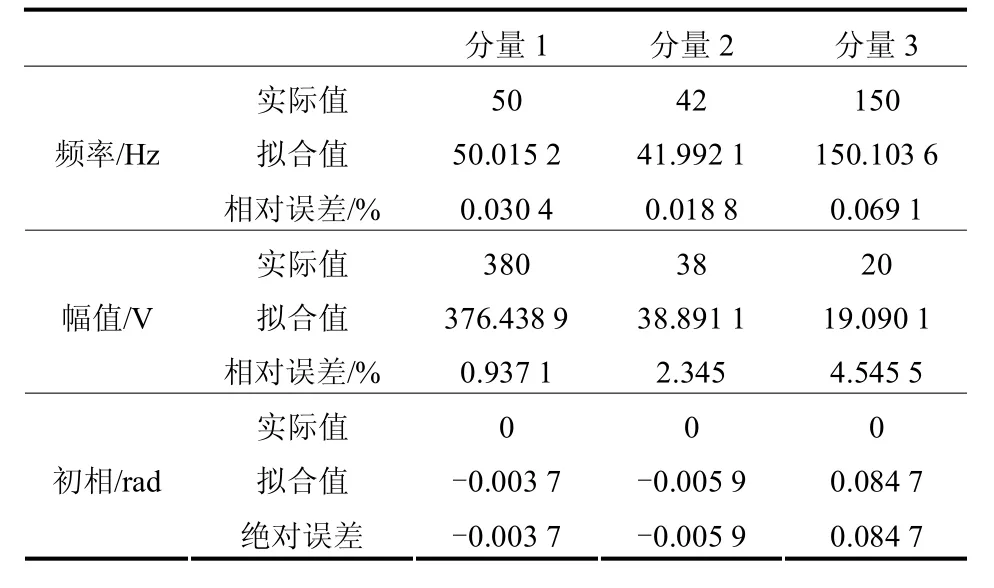
表5 谐波、电压闪变信号特征参数Table 5 Signal characteristic parameters of harmonic and voltage flicker

2) 当稳态与暂态电能质量扰动同时存在时，由第1节知本文算法可准确地判断是否包含暂态扰动及扰动的起止时间。首先使用文献[11]所述方法辨识扰动类型，并在暂态扰动发生时间之外重新选择样本，使用改进Prony方法进行分析，得到其特征参数。

4 结论

1) 选择db4小波来分析区别暂态与稳态电能质量扰动，并通过选择最优重构层数提取暂态扰动波形，得到了更好的重构信号，便于对暂态扰动进行分类。

2) 对Prony方法进行改进，得到了优化的Prony模型，其在对含有谐波、间谐波和小噪声干扰信号进行识别时依然具有较高的准确性。

3) 对经典电能质量扰动模型进行分析，可辨识出暂态扰动的种类与稳态扰动信号的特征参数，提出分析混合电能质量扰动问题的普遍方法。

[1] 张逸, 林焱, 吴丹岳. 电能质量监测系统研究现状及发展趋势[J]. 电力系统保护与控制, 2015, 43(2): 138-147. ZHANG Yi, LIN Yan, WU Danyue. Current status and development trend of power quality monitoring system[J]. Power System Protection and Control, 2015, 43(2): 138-147.

[2] 姚致清, 赵倩, 刘喜梅. 基于准同步原理的逆变器并网技术研究[J]. 电力系统保护与控制, 2011, 39(24): 123-126, 131. YAO Zhiqing, ZHAO Qian, LIU Ximei. Research on grid-connected technology of inverter based on quasi synchronous principle[J]. Power System Protection and Control, 2011, 39(24): 123-126, 131.

[3] 许珉, 刘玮. 加8项余弦窗插值FFT算法[J]. 电力系统保护与控制, 2015, 43(11): 27-32. XU Min, LIU Wei. An interpolation FFT algorithm based on 8-term cosine window[J]. Power System Protection and Control, 2015, 43(11): 27-32.

[4] 唐炬, 樊雷, 张晓星, 等. 用谐波小波包变换法提取GIS局部放电信号多尺度特征参数[J]. 电工技术学报, 2015, 30(3): 250-257. TANG Ju, FAN Lei, ZHANG Xiaoxing, et al. Multi-scale feature parameters extraction of GIS partial discharge signal with harmonic wavelet packet transform[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 250-257.

[5] 黄南天, 张卫辉, 蔡国伟, 等. 采用改进多分辨率快速S变换的电能质量扰动识别[J]. 电网技术, 2015, 39(5): 1412-1418. HUANG Nantian, ZHANG Weihui, CAI Guowei, et al. Power quality disturbances classification with improved multiresolution fast S-transform[J]. Power System Technology, 2015, 39(5): 1412-1418.

[6] 聂永辉, 荣令玉, 张立艳. 数学形态学和ESPRIT在低频振荡分析中的应用[J]. 电力系统及其自动化学报, 2012, 24(6): 123-127. NIE Yonghui, RONG Lingyu, ZHANG Liyan. Low frequency oscillation analysis using mathematical morphology and ESPRIT[J]. Proceedings of the CSU-EPSA, 2012, 24(6): 123-127.

[7] 刘明才. 小波分析及其应用[M]. 2版. 北京: 清华大学出版社, 2013: 10-18.

[8] 鲁波涌, 黄文清. 结合小波变换和能量算子的电压暂降检测方法[J]. 电工技术学报, 2011, 26(5): 171-177. LU Boyong, HUANG Wenqing. Hybrid wavelet-energy operator method for voltage sag detection[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 171-177.

[9] The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Technical Gazette, 2015, 22(1): 43-49.

[10] 李正明, 徐敏, 潘天红, 等. 基于小波变换和 HHT的分布式并网系统谐波检测方法[J]. 电力系统保护与控制, 2014, 42(4): 34-39. LI Zhengming, XU Min, PAN Tianhong, et al. A harmonic detection method for distributed connected grid system by using wavelet transform and HHT[J]. Power System Protection and Control, 2014, 42(4): 34-39.

[11] 李玉洁, 方瑞明. 基于改进加权灰关联分析法的风电机组可靠性研究[J]. 电力系统保护与控制, 2015, 43(14): 63-69. LI Yujie, FANG Ruiming. Reliability assessment for wind turbine based on weighted degree of improved grey incidence[J]. Power System Protection and Control, 2015, 43(14): 63-69.

[12] CHO S H, PARK C H, HAN J H, et al. A waveform distortion evaluation method based on a simple half-cycle RMS calculation[J]. IEEE Transactions on Power Delivery, 2012, 27(3): 1461-1467.

(编辑 魏小丽)

Power quality disturbance analysis based on wavelet transform and improved Prony method

REN Zihui, LIU Haoyue, XU Jinxia
(School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China)

The traditional analysis method for power quality only analyzes one kind of specific problems. In order to effectively distinguish and identify common power disturbance signal, an algorithm combining wavelet analysis with Prony method is proposed. Firstly, the wavelet multi-resolution analysis is introduced, the appropriate wavelet function is proposed to decompose the disturbance signal and whether the decomposed signal modulus maxima exist is judged. Thus the steady state and transient state power quality disturbance problems are distinguished. For the transient disturbance problem, Mallat refactoring layer is optimized, the transient disturbance waveform are extracted and the type of disturbance is distinguished. For the steady disturbance problem, the process of estimating system order by Prony method and the accuracy of parameter identification are improved. Finally, mixed disturbance signals are analyzed and the simulation and experimental verification are performed by Matlab. Results of simulation and experiments show that the proposed method algorithm can accurately identify the various types of power quality disturbance signal.

power quality; wavelet analysis; Mallat reconstruction; Prony method; parameter identification

10.7667/PSPC151107

：2015-08-04

任子晖(1962-)，男，教授，博士生导师，研究方向为电能质量分析与控制；E-mail: thecronus@sina.com

刘昊岳(1991-)，男，通信作者，硕士研究生，研究方向为电能质量分析与控制；E-mail: liuhaoyue@cumt.edu.cn

徐进霞(1990-)，女，硕士研究生，研究方向为电力系统智能控制技术。E-mail: 1159895580@qq.com