电力电子接口新能源并网的暂态电压稳定机理研究
陈 磊,刘永奇,戴远航,闵 勇,张玮灵,侯凯元
(1.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京100084;2.东北电网有限公司,辽宁 沈阳110181)
电力电子接口新能源并网的暂态电压稳定机理研究
陈 磊1,刘永奇2,戴远航1,闵 勇1,张玮灵1,侯凯元2
(1.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系),北京100084;2.东北电网有限公司,辽宁 沈阳110181)
为掌握大规模风电、光伏等新能源并网给电力系统稳定性带来的影响,对采用电力电子接口的新能源发电接入系统的暂态电压稳定机理进行了研究。首先对机电暂态过程中新能源发电进行简化建模。采用电力电子变换器的风电、光伏等电源功率控制快速灵活,在机电暂态过程中可以忽略功率调节的快动态,其特性简化为功率平衡代数方程,系统动态方程为微分代数方程。基于微分代数系统稳定性研究了新能源并网的暂态电压稳定机理,暂态过程中轨迹可能遇到微分代数方程的奇异点,对应系统发生暂态电压失稳,此时新能源发电对应的功率平衡方程无解。通过仿真验证了该机理,并在风火打捆送出系统中揭示了系统失稳模式的变化,风电功率增加时,系统失稳模式由同步机主导的功角失稳变为风电主导的电压失稳。
新能源;电力电子接口;暂态电压稳定;微分代数方程;奇异点
0 引言
风电、光伏等新能源近年来发展迅速,并网后给电力系统的安全稳定性带来很大影响。电力电子变换器在新能源发电中获得广泛应用,双馈风机、直驱风机、光伏发电均采用了电力电子变换器作为和电网的接口,这使得新能源发电的动态特性完全不同于传统的同步发电机,会极大的改变系统的稳定特性。大量文献[1-4]研究了风电对功角稳定的影响,包括小扰动稳定和暂态稳定。除了功角稳定以外,电压稳定是大规模风电接入系统需要重点关注的问题。文献[5-6]研究了风电接入系统的静态电压稳定问题,文献[7-9]则主要研究暂态电压稳定问题。目前对异步风机暂态电压稳定的机理已有较为明确的认识,但对双馈或直驱风机的暂态电压稳定机理并没有成熟公认的结论。光伏对系统稳定性的影响也已有部分研究[10]。已有研究大多以针对具体系统的仿真分析为主,缺乏对机理的研究,不利于对该问题的深入认识以及对应控制措施的研究。
文献[3]从理论上分析含风电场的电力系统暂态稳定性,研究风电场注入功率对同步机加速面积和减速面积的影响,因为风电场的快速调节,机电暂态过程中风电场输出功率波动的幅度和时间比同步发电机都要小得多,因此将风电场的功率等值为同步发电机的机械功率进行研究。必要的归纳简化是机理研究的一般前提。本文也从新能源发电注入功率特性的分析和简化出发,基于微分代数方程(Differential Algebraic Equation,DAE)的稳定性理论,研究电力电子接口新能源并网的暂态电压稳定机理,并进行了详细的仿真分析,说明新能源功率增加导致的稳定性质变化以及功角失稳、电压失稳的区别。需要说明的是,本文在研究风电、光伏和电力系统动力学特性之间的相互作用时,暂不考虑风速、光照不确定的影响,假设风速、光照为一定值。
1 机电暂态过程中新能源发电的简化建模
在研究风电、光伏对电力系统稳定性的影响时,目前大量文献的做法是建立详细的模型,然后通过时域仿真进行分析。这种做法的优点是对于所研究的具体对象,能够获得关于系统稳定性的准确结论,但缺点是模型复杂,而且不同厂家不同型号的风机、光伏差异很大,不便于掌握稳定性的机理,难以获得通用的结论。类似于同步发电机暂态稳定的研究,分析机理时采用简化模型如经典模型,本文研究新能源接入系统的稳定机理时,也采用简化模型。
新能源发电影响电力系统稳定性的关键,是动态过程中注入系统有功、无功的变化[1,3]。简化建模的核心就是保留故障中注入系统有功、无功的动态过程[11]。双馈、直驱风机和光伏发电都通过电力电子变换器和电力系统之间接口,可以快速灵活的进行功率控制。和同步发电机相比,采用电力电子接口的变速风机功率控制的速度快得多。根据实测数据,双馈风机有功和无功进入稳态所需的时间大约在0.15 s左右[11],直驱风机一般只需要0.04~0.05 s,光伏的时间也在0.05 s左右[12]。因此,采用电力电子接口的新能源发电功率调节的时间常数远小于机电暂态的时间常数。根据多时间尺度动力系统建模理论[13-14],两个动态过程时间常数差别很大时,可建立仅保留正常速率变量的降阶模型,忽略快动态,将其用代数方程表示。双馈风电机组通用模型和详细模型相比,就是忽略了变流器、网侧控制器以及发电机的定转子动态,将其用代数方程表示[15]。本文进一步简化,研究机电暂态时,忽略新能源发电功率调节的快动态,认为功率能够快速达到控制策略的目标稳态(即文献[13-14]中的快流形),输出功率用代数方程描述,简化为功率注入。图1(a)是实测的某1.5 MW直驱风机在电压跌落至0.3时的功率输出特性,文献[16]中的风电场实测功率特性、以及文献[12]中采用详细模型仿真得到的光伏发电功率特性都和图1(a)是类似的。从图1(a)可以看到扰动后有功无功均很快达到稳态,没有明显振荡过程,忽略快动态是合理的。
不同风机、光伏的功率控制模式差异很大,表征输出功率特性的代数方程也不同。以风机为例,稳态运行时风机的功率控制模式基本相同,本文采用最典型的方式,有功控制为最大功率点跟踪模式,无功控制为定功率因数模式,固定功率因数为 1。电网扰动过程中,风机注入功率一般为机端电压的函数,而且不同电压范围时控制策略不同,表现为分段函数的形式。因此,风电的输出特性为如下形式的代数方程:故障期间 Pw= fon(U), Qw=gon(U ) ,故障清除后 Pw= fpost(U), Qw= gpost(U),U为机端电压,上述函数的具体形式决定于风机控制策略,而且具有分段等强非线性。
为了继续进行研究,本文选取一种简单典型的控制策略为例进行分析。对于有功功率控制,有的风机故障期间有功电流基本不变(如图 1(a)),有的会降低有功电流。本文假设故障期间新能源发电控制有功电流为0,则故障期间有功功率为0。即使有功电流大于 0,由于严重故障时机端电压一般都跌落得很低,有功功率也很小。故障清除后电压恢复,风机恢复有功功率,有的风机存在功率爬坡过程,本文也暂不考虑,认为故障清除后有功功率迅速恢复为故障前的最大功率点跟踪的设定值。无功功率的控制策略更加多样化,图1(a)中的风机采用了无功优先的控制策略。本文考虑较为不利的情况,故障期间和故障清除后风机都不输出无功功率,即无功功率恒为零。简化的风电输出特性如图1(b)所示。光伏的输出有功、无功控制策略和风机尤其是直驱风机很多情况下类似。采取上述简化后,新能源发电的输出特性简化为如下的代数方程:故障期间,Pw= 0, Qw= 0;故障清除后, Pw= Pw0, Qw= 0。上述简化忽略了变速风机和光伏发电中由电力电子变换器所主导的快动态,而且功率控制策略也只是一种特殊情况,但是上述简化保留了采用电力电子接口的新能源发电最基本的输出外特性,对于机理研究是有效的。对于暂态稳定研究而言,根据具体的控制策略,新能源发电功率的函数形式发生变化,但风电的输出特性仍然是代数方程,后续的机理分析仍然适用。
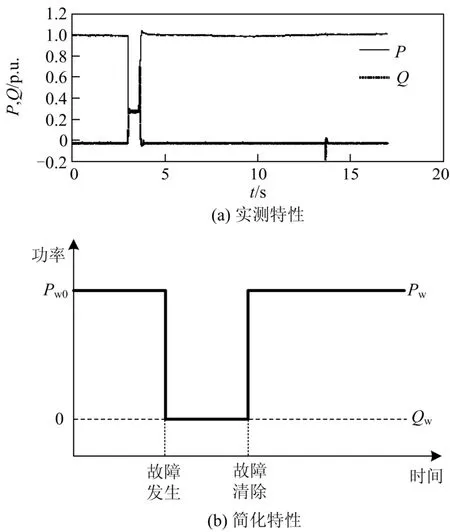
图1 实测的与简化的风电输出特性Fig. 1 Actual and simplified wind power output characteristics
本节的简化建模是通过对大量实测响应的总结分析获得的,和实际情况相比,主要区别是忽略了故障发生和清除时功率的短时快速振荡[11,16],这些振荡对系统机电暂态的影响不大,在进行机理研究时可以忽略,因此,本节的简化建模用于分析新能源并网后系统机电暂态过程及稳定性是合理的,需要注意的是根据新能源发电的实际功率控制策略,调整表示其功率输出特性的代数方程的形式。此外,上述分析假设故障中新能源始终接入系统,即具有低电压穿越能力。
2 DAE系统的奇异性和暂态电压失稳
根据上节的分析,由于电力电子接口的快速调节作用,机电暂态过程中新能源发电的输出特性简化为静态功率注入模型,则在系统的动态方程中新能源特性用功率平衡方程表示,是一个代数方程,整个系统的动态方程为如下的DAE系统

式中:x为系统状态变量,例如发电机功角和转速;y为系统代数变量,一般为节点的电压U和相角q。
新能源特性包含在0 (,)gxy= 中,假设节点i为新能源节点,其对应的功率平衡方程如下

在故障后系统中, Pwi= Pw0i, Qwi= 0, Pw0i为故障前功率设定值。如果新能源发电采用不同的控制策略而出现不同的外特性,其功率的函数形式发生变化会导致式(2)发生变化,但仍为代数方程,这是因为忽略了新能源发电的快动态。
根据DAE的稳定边界理论[17],对于方程(1),记
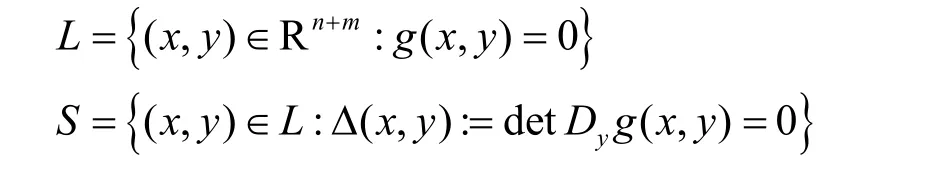
L称为约束面,DAE系统的所有轨迹都必须在L中。S为系统奇异面,S中的点称为奇异点,而 L S中的点称为正则点。对于正则点 ( x0,y0)Î L S,由隐函数定理在 x = x0附近存在唯一的 y = y(x)使(x,y(x) )Î L ,代入式(1)可得

方程(1)在 ( x0,y0)有唯一解。但对于奇异点(xS,yS)Î S ,方程(1)在 ( xS,yS)附近的解不存在。DAE系统的轨迹在某个时刻能够延拓到 ( xS,yS),但不能再向前延伸,因为(1)中的代数方程变得无解了。
在电力系统中,DAE系统轨迹遇到奇异点对应暂态电压失稳[18],此时系统的功率平衡方程(潮流方程)无解,失稳的形式是代数变量失稳,即电压失稳。新能源发电特性简化为式(2)所示的代数方程时,也可能在故障后暂态过程中出现代数方程奇异的情况,此时对应新能源发电节点电压发生崩溃。
3 风电接入系统的暂态电压稳定机理分析
下面以风电为例进行分析,所获得的结论对于光伏也是适用的。在图2所示的简单系统中对上述机理进行分析。同步机和风电场分别经过线路接到一个公共母线,然后接入无穷大系统。系统中同步机采用经典模型,发电机内节点表示为EÐd ,E为发电机内电势,d为发电机功角,暂态电抗并入网络。无穷大母线电压为 UsÐ 0 。系统参数 X1=0.2,X2=0.3,X3=0.4,Us=1.0,E=1.3,TJ=8.0 s,D=5.0。
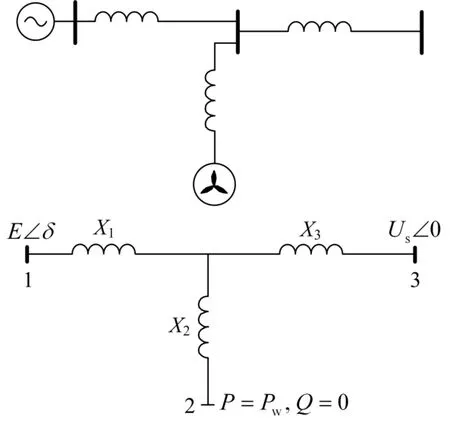
图2 简单系统及其等效电路Fig. 2 A simple system and its equivalent circuit
列写故障后系统 DAE方程。系统的状态变量包括 ,dw,分别为发电机功角和转速,系统的代数变量包括 ,Uq,分别为风电场节点的电压幅值和相角。系统微分方程为发电机转子运动方程:
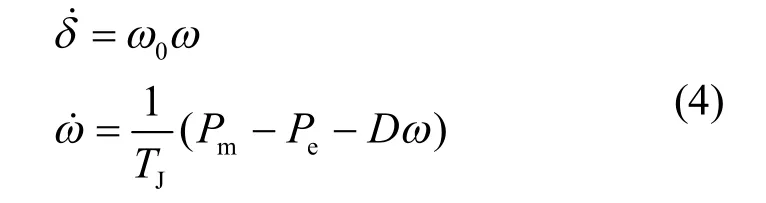
式中,eP为发电机注入网络的电磁功率,对网络进行星形-三角形变换后,可得电磁功率的表达式为
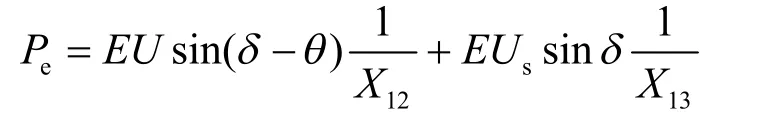
代数方程为风电功率平衡方程。故障后机电暂态过程中风电有功功率为恒定值w0P ,无功为0,代数方程如下:
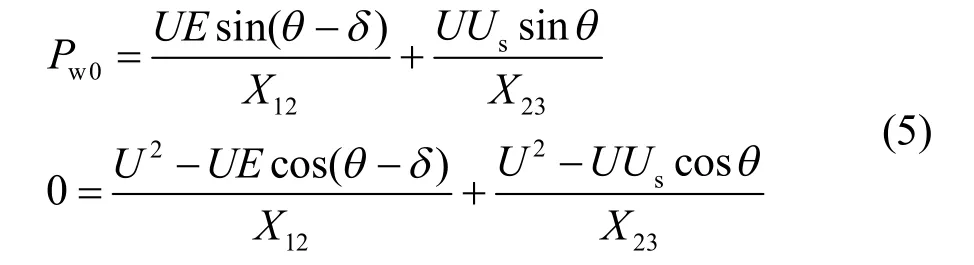
代数方程式(5)中,U ,q为待求量,受到状态变量d的影响,暂态过程中当d变化时,方程的解U,q就会发生变化。有可能出现这样的情况:当d增大到某一个值以后,上述代数方程变为无解,从电力系统稳定性的角度理解,潮流方程无解对应的是系统发生电压失稳。下面分析两种不同的情形。
1) 风电功率小,系统失稳为功角失稳
同步机功率 Pm=1.4,风电功率 Pw0=0.3。对于代数方程式(5),当d变化时,方程的解U的变化如图3所示。在d从0到180º的变化范围内,代数方程始终有解,不会出现电压失稳的问题。图3中同时画出了同步发电机的功角特性曲线,曲线和机械功率有两个交点,分别对应稳定和不稳定平衡点,故障导致轨迹越过不稳定平衡点后则系统功角失稳。图4是公共母线瞬时三相短路故障临界失稳的仿真曲线。失稳时同步机失去同步,功角持续增加,同步机失步导致风电场电压周期性波动。
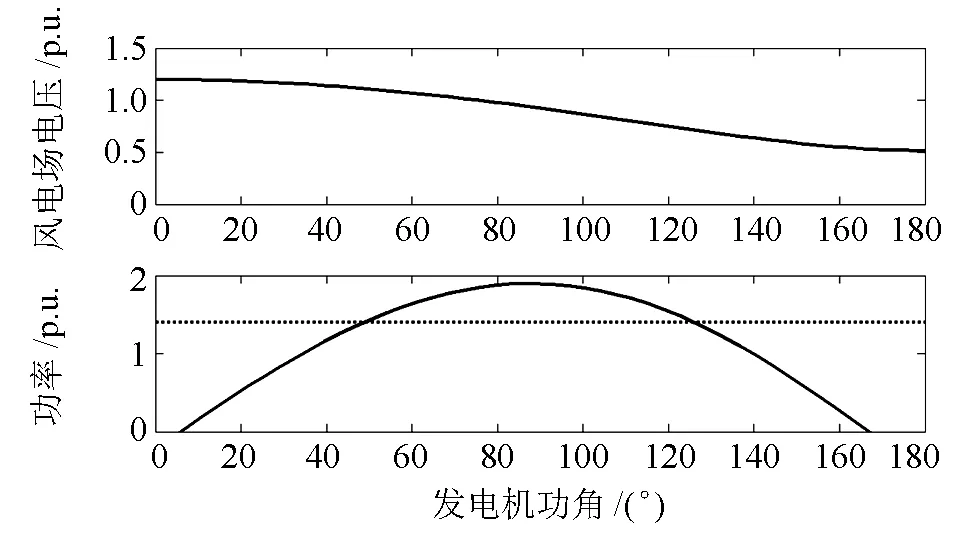
图3 风电功率较小时代数方程的解Fig. 3 Solutions of algebraic equations with small wind power
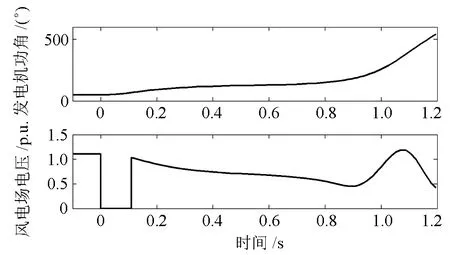
图4 功角失稳时的系统轨迹Fig. 4 Trajectories of rotor angle instability
2) 风电功率大,系统失稳为电压失稳
同步机功率mP=0.8,风机功率w0P =0.9。对于代数方程式(5),当d变化时,方程的解U的变化如图5所示。当功角增加到100º左右时,代数方程变为无解,系统达到电压稳定的临界点,该点是DAE系统的奇异点。如果故障过程中发电机功角增加遇到该奇异点,则系统发生电压崩溃。图5中同时画出了同步发电机的功角特性曲线,曲线和机械功率只有一个交点,功角失稳对应的不稳定平衡点消失。
图6是临界失稳的仿真曲线。故障清除后随着发电机功角增加,系统遇到奇异点,此时 DAE系统的轨迹无法继续延伸,对应系统发生电压崩溃,崩溃点处发电机的功角并不大。为了进一步说明电压崩溃点就是奇异点,对于故障后轨迹上的每个点,求取代数方程(5)对代数变量 U ,q的导数矩阵 Dyg,然后求其行列式的绝对值如图6所示,沿着故障后轨迹迅速下降,下降到 0时Dyg奇异,轨迹遇到奇异点,系统也发生电压崩溃。

图5 风电功率较大时代数方程的解Fig. 5 Solutions of algebraic equations with large wind power
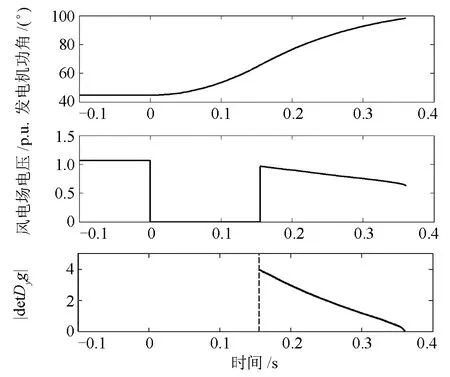
图6 电压失稳时的系统轨迹Fig. 6 Trajectories of voltage instability
4 详细模型仿真分析
上节利用简化模型分析了新能源并网的暂态电压稳定机理。已有文献研究新能源并网的稳定问题时,主要方法是先建立新能源发电的详细模型,然后进行仿真研究。为和已有研究进行比较,本节也采用详细模型进行仿真,对上节的机理进行分析,仿真工具采用DIgSILENT。建立图2所示的系统,网络参数不变,同步发电机采用详细模型,风机采用DIgSILENT中自带的双馈风机模型和典型参数。公共母线处t=0s时发生瞬时三相短路故障。
1) 风电功率小,功角失稳的情形
临界失稳时的同步机转速和功角如图7所示,转速和功角都持续增加,导致风电场电压周期波动,如图8所示。风电场有功无功的变化如图9,和图1中的简化输出特性很接近。风电功率小时,系统失稳为功角失稳,同步机失去同步导致电压周期性波动,风电场功率由于电压波动略有波动,但基本维持故障前设定值,失稳的是同步机。
风电功率恢复后,将其作为静态功率注入,构建式(5)所示的代数方程并沿着轨迹计算结果如图 8 。可以看到在故障清除后一直大于0,轨迹未遇到奇异点,系统未发生电压失稳。
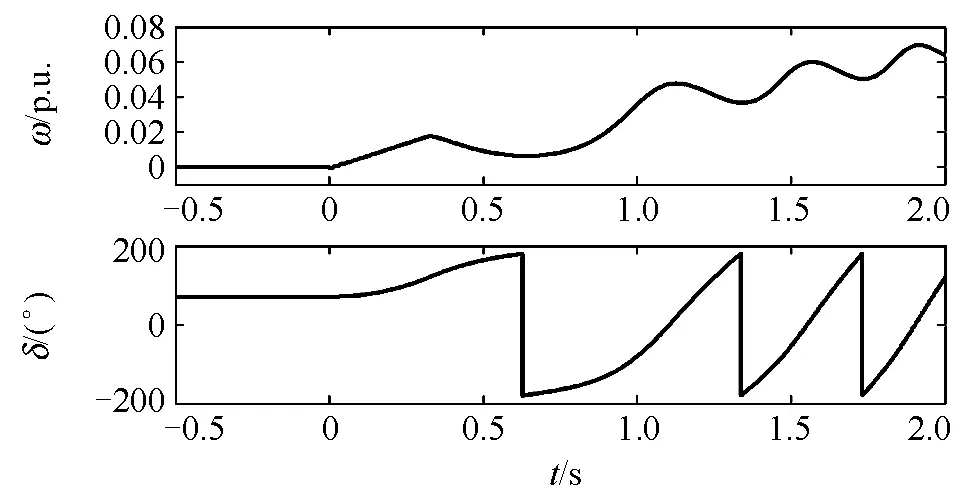
图7 功角失稳时的同步机转速和功角Fig. 7 Synchronous generator speed and rotor angle of rotor angle instability
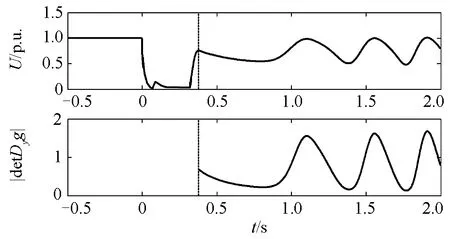
图8 功角失稳时的风电场电压Fig. 8 Wind farm voltage of rotor angle instability
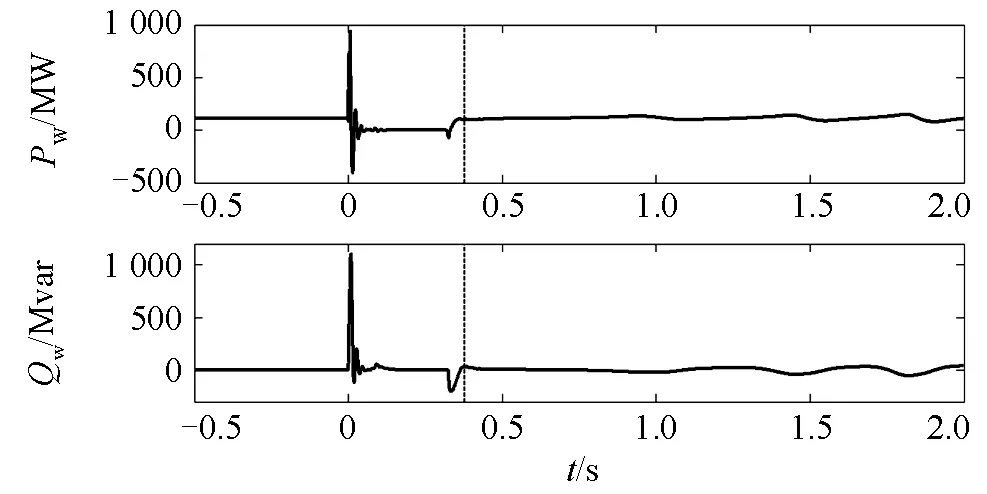
图9 功角失稳时的风电场有功无功Fig. 9 Wind farm active and reactive power of rotor angle instability
2) 风电功率大,电压失稳的情形
增大风电功率并减小同步机功率。临界失稳时的同步机转速和功角如图10所示,系统未发生功角失稳。但风电场电压不能维持稳定,如图11所示,故障清除瞬间电压恢复,但随着发电机功角的摆开,电压不断降低,0.705 s左右发生电压崩溃。图 12显示的风电场有功无功曲线,在故障清除后短时间内功率维持在故障前设定值,但在电压崩溃点处迅速失去稳定。图10中的同步机转速和功角则维持正常,并未表现出失稳,系统中失稳的是风电。
同时,比较图8和图11可以看到,图11中电压波动的频率远高于图 8 。功角稳定是由同步发电机的机电暂态过程主导的,动态过程时间常数较大;而电压失稳是由采用电力电子接口的风电主导的,动态过程时间常数很小。由此导致了失稳时的表现不同。
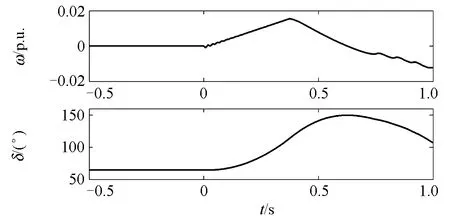
图10 电压失稳时的同步机转速和功角Fig. 10 Synchronous generator speed and rotor angle of voltage instability
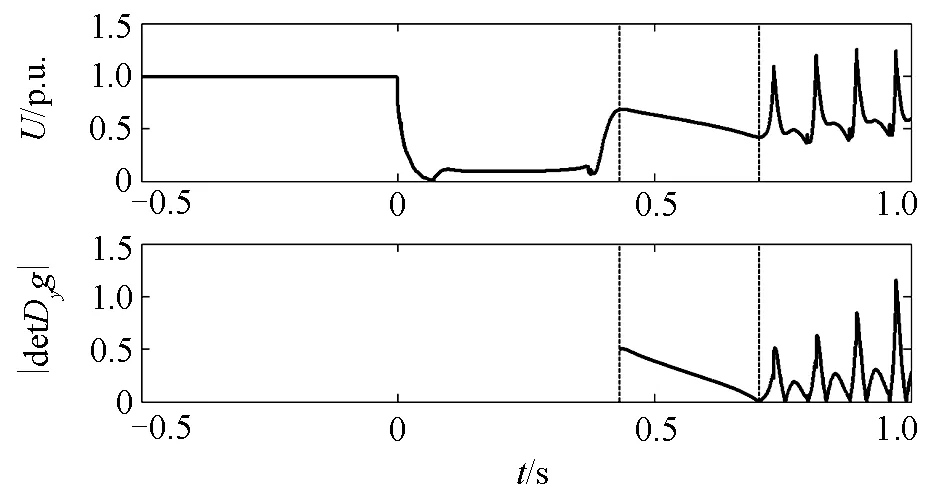
图11 电压失稳时的风电场电压Fig. 11 Wind farm voltage of voltage instability
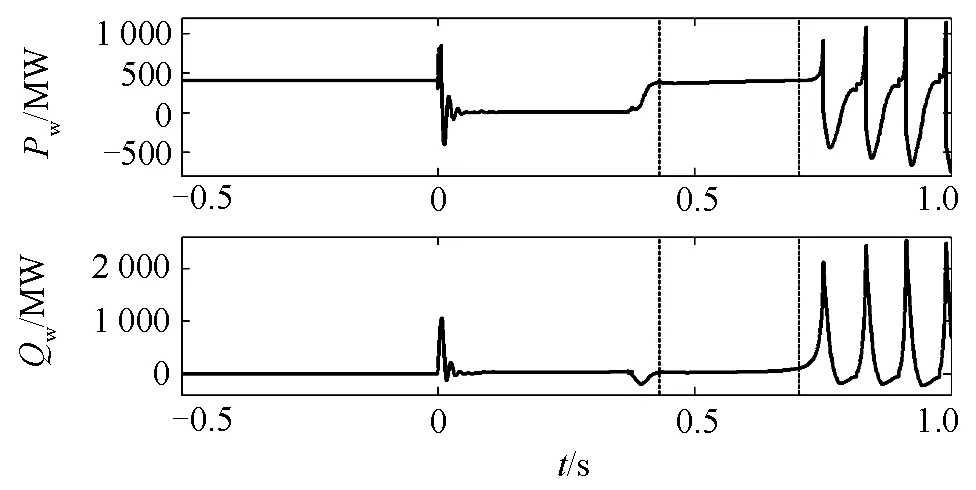
图12 电压失稳时的风电场有功无功Fig. 12 Wind farm active and reactive power of voltage instability
本节仿真采用的 DIgSILENT软件是目前公认的对风电的模拟效果较好的仿真软件。DIgSILENT详细模型的仿真结果和基于简化模型提出的机理是吻合的,功角、电压、输出功率、代数方程奇异性的结果都相互印证,验证了本文结论的有效性。
5 结语
本文基于简化模型研究电力电子接口新能源并网的暂态电压稳定机理。机电暂态过程中,采用电力电子接口的新能源发电可以忽略变换器主导的快动态,简化为静态功率注入模型,则系统动态方程为微分代数方程,轨迹遇到奇异点对应着系统发生暂态电压崩溃,此时新能源发电对应的功率平衡方程无解。在风火打捆送出示例系统中进行了仿真分析,验证了该机理,同时发现随着风电功率的增加,系统失稳模式会由功角失稳变为电压失稳。新能源大规模接入会导致系统稳定特性发生很大的变化,原有的针对功角稳定的分析控制手段可能都需要进行调整。
本文的机理研究忽略了由电力电子变换器主导的功率调节的快动态,用代数方程表示。应用于实际系统时,风电、光伏对应代数方程中有功无功的表达式和具体的控制策略有关,控制策略变化时(如提供动态无功支撑,有功恢复速率受限),代数方程的形式变化,本文所提的机理仍然适用,但具体电网的稳定性结论会发生变化。后续研究将集中于大系统中不同新能源控制策略的分析,以及稳定性质改变后控制方法。
[1] VITTAL E, O'MALLEY M, KEANE A. Rotor angle stability with high penetrations of wind generation[J]. IEEE Transactions on Power Systems, 2012, 27(1): 353-362.
[2] 和萍, 文福拴, 薛禹胜, 等. 风力发电对电力系统小干扰稳定性影响述评[J]. 电力系统保护与控制, 2014, 26(1): 1-7. HE Ping, WEN Fushuan, XUE Yusheng, et al. Survey on impact of wind power on small signal stability in power system[J]. Proceedings of the CSU-EPSA, 2014, 26(1): 1-7.
[3] 林俐, 杨以涵. 基于扩展等面积定则的含大规模风电场电力系统暂态稳定性分析[J]. 电力系统保护与控制, 2012, 40(12): 105-110. LIN Li, YANG Yihan. Analysis of transient stability of power system including large scale wind power based on the extended equal area rule[J]. Power System Protection and Control, 2012, 40(12): 105-110.
[4] 舒进, 都劲松, 王靖程, 等. 基于奇异摄动降阶的风电接入系统阻尼分析[J]. 电力系统保护与控制, 2014,42(19): 18-25. SHU Jin, DU Jinsong, WANG Jingcheng, et al. System damping analysis after wind power integration using singular perturbation system reduction[J]. Power System Protection and Control, 2014, 42(19): 18-25.
[5] VITTAL E, O’MALLEY M, KEANE A. A steady-state voltage stability analysis of power systems with high penetrations of wind[J]. IEEE Transactions on Power Systems, 2010, 25(1): 433-442.
[6] 鲍海波, 韦化. 考虑风电的电压稳定概率评估的随机响应面法[J]. 中国电机工程学报, 2012, 32(13): 77-85. BAO Haibo, WEI Hua. A stochastic response surface method for probabilistic evaluation of the voltage stability considering wind power[J]. Proceedings of the CSEE, 2012, 32(13): 77-85.
[7] 范高锋, 迟永宁, 赵海翔, 等. 用STATCOM提高风电场暂态电压稳定性[J]. 电工技术学报, 2007, 22(11): 158-162. FAN Gaofeng, CHI Yongning, ZHAO Haixiang, et al. Transient voltage stability enhancement of wind farm using STATCOM[J]. Transactions of China Electrotechnical Society, 2007, 22(11): 158-162.
[8] 魏晓光, 迟永宁, 魏晓云, 等. 电压源换相高压直流输电改善异步发电机风电场暂态电压稳定性的研究[J].电工技术学报, 2008, 23(5): 100-107. WEI Xiaoguang, CHI Yongning, WEI Xiaoyun, et al. Transient voltage stability enhancement of induction generator-based wind farm by VSC-HVDC[J]. Transactions of China Electrotechnical Society, 2008, 23(5): 100-107.
[9] 吴丽娜, 邵龙, 刘观起, 等. 含无功补偿装置的风电并网系统暂态电压稳定性研究[J]. 电网与清洁能源, 2014, 30(9): 66-71. WU Lina, SHAO Long, LIU Guanqi, et al. Study on transient voltage stability of wind farm incorporated system with reactive power compensation devices[J]. Power System and Clean Energy, 2014, 30(9): 66-71.
[10] 盛四清, 侯磊, 范辉, 等. 光伏电站接入孤立电网的动态建模与稳定性分析[J]. 电力系统保护与控制, 2012, 40(23): 126-131. SHENG Siqing, HOU Lei, FAN Hui, et al. Analysis on dynamic modeling and stability of isolated grid with photovoltaic station connected[J]. Power System Protection and Control, 2012, 40(23): 126-131.
[11] 张慧玲, 郝思鹏, 袁越, 等. 基于实测数据的双馈风电机组外特性研究及简化建模[J]. 电力系统保护与控制, 2013, 41(17): 82-87. ZHANG Huiling, HAO Sipeng, YUAN Yue, et al. Research on external characteristics of DFIG and simplified modeling based on testing data[J]. Power System Protection and Control, 2013, 41(17): 82-87.
[12] 闫凯, 张保会, 瞿继平, 等. 光伏发电系统暂态建模与等值[J]. 电力系统保护与控制, 2015, 43(1): 1-8. YAN Kai, ZHANG Baohui, QU Jiping, et al. Photovoltaic power system transient modeling and equivalents[J]. Power System Protection and Control, 2015, 43(1): 1-8.
[13] 刘永强, 杨志辉, 唐云, 等. 多时间尺度电力系统的模型降阶及稳定性分析(一)基本理论[J]. 电力系统自动化, 2003, 27(1): 5-10. LIU Yongqiang, YANG Zhihui, TANG Yun, et al. Order reduction and stability analysis for multi-time scale power systems part one fundamental theory[J]. Automation of Electric Power Systems, 2003, 27(1): 5-10.
[14] 刘永强, 雷文, 吴捷, 等. 多时间尺度电力系统的模型降阶及稳定性分析(二)电力系统的降阶与中长期失稳[J]. 电力系统自动化, 2003, 27(2): 45-51. LIU Yongqiang, LEI Wen, WU Jie, et al. Order reduction and stability analysis for multi-time scale power systems part one order reduction and loss of mid-term and longterm stability[J]. Automation of Electric Power Systems, 2003, 27(2): 45-51.
[15] 潘学萍, 鞠平, 吴峰, 等. 双馈风电机组模型结构讨论[J]. 电力系统自动化, 2015, 39(5): 7-14. PAN Xueping, JU Ping, WU Feng, et al. Discussion on model structure of DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2015, 39(5): 7-14.
[16] 张明理, 徐建源, 李佳珏. 含高渗透率风电的送端系统电网暂态稳定研究[J]. 电网技术, 2013, 37(3): 740-745. ZHANG Mingli, XU Jianyuan, LI Jiayu. Research on transient stability of sending power grid containing high proportion of wind power[J]. Power System Technology, 2013, 37(3): 740-745.
[17] VENKATASUBRAMANIAN V, SCHATTLER H, ZABORSZKY J. Dynamics of large constrained nonlinear systems-a taxonomy theory[J]. Proceedings of the IEEE, 1995, 83(11): 1530-1561.
[18] 刘斌, 陈磊, 闵勇. 考虑暂态电压稳定的低压减载地点选择[J]. 电力系统自动化, 2008, 32(5): 11-14. LIU Bin, CHEN Lei, MIN Yong. Determination of the location of under-voltage load shedding considering transient voltage stability[J]. Automation of Electric Power Systems, 2008, 32(5): 11-14.
(编辑 张爱琴)
Study on the mechanism of transient voltage stability of new energy source with power electronic interface
CHEN Lei1, LIU Yongqi2, DAI Yuanhang1, MIN Yong1, ZHANG Weiling1, HOU Kaiyuan2
(1. State Key Lab of Control and Simulation of Power Systems and Generation Equipment (Dept of Electrical Engineering, Tsinghua University), Beijing 100084, China; 2. Northeast China Grid Company Limited, Shenyang 110181, China)
To clarify the influence of large scale new energy source like wind power and photovoltaics on power system stability, the mechanism of transient voltage stability of new energy source with power electronic interface is studied. The simplified model of new energy source in electro-mechanic transient is first studied. Variable speed wind turbines and photovoltaics with power electronic interface can control the power quickly and flexibly. In power system electro-mechanic transients, the fast dynamics of power adjustment can be neglected, and the new energy source characteristic is simplified to power balance algebraic equation. The system dynamic equation is a differential algebraic equation. According to the stability theory of differential algebraic systems, the trajectory meeting a singular point of the differential algebraic equation corresponds to transient voltage instability in the system. The power balance equation of the new energy source becomes unsolvable at the point. Simulation results validate the mechanism, and reveal the variation of instability mode of a wind-thermal-bundled sending system. As the wind power increases, the instability mode of the system changes from rotor angle instability dominated by synchronous generator to voltage instability dominated by wind power.
This work is supported by National Science and Technology Infrastructure Program (No. 2013BAA01B03), National Natural Science Foundation of China (No. 51377002), and Northeast China Grid Company Limited.
new energy source; power electronic interface; transient voltage stability; differential algebraic equation; singular point
10.7667/PSPC150481
:2016-02-01
陈 磊(1982-),男,博士,副教授,研究方向为电力系统动态分析与控制;E-mail: chenlei08@tsinghua.edu.cn
刘永奇(1965-),男,高工,研究方向为电网调度运行;
戴远航(1990-),男,博士研究生,研究方向为电力系统动态分析与控制。E-mail: daiyuanhang09@163.com
国家科技支撑计划项目(2013BAA01B03);国家自然科学基金项目(51377002);东北电网有限公司科技项目

