基于微分对策央行与公众间博弈模型的研究

程潘红

基于微分对策央行与公众间博弈模型的研究

程潘红

摘要:央行与公众之间的博弈属于宏观经济博弈。文章首先主要从经济增长理论的角度建立两者博弈的状态方程与目标泛函。具有微分形式的状态方程与目标泛函组成该博弈的微分对策模型。然后运用双方极值理论中的Hamilton函数、伴随方程与边界条件求解模型，分别得到央行与公众博弈的最优策略。最后对模型结果进行说明，并给出央行与公众的最优控制变量之间满足的关系式，即投资增长率与实际物价水平增长率及期望物价水平增长率之间的关系，从而得到该博弈模型的解。

关键词:微分对策；GDP水平；物价水平；双方极值理论

现代市场经济国家的宏观调控政策目标一般包括稳定物价水平，促进经济增长，充分就业，国际收支平衡。但因为后三个目标是同向变化的，因此现代西方经济学都将货币政策目标归纳为稳定物价水平和促进经济增长。我国是发展中国家，在保证促进经济又好又快的发展这个首要目标时，必须同时考虑物价水平的稳定性。因此我国货币政策是双目标的。

央行与公众之间的博弈属于宏观经济博弈，在基于双目标货币政策的前提下，陈学彬[1]

从货币供给增长率的角度考虑完全信息条件下央行与公众之间的博弈行为，寻求到货币供给增长率与期望经济增长率及潜在经济增长率之间的关系，使得双重目标成本最小，达到博弈均衡。本文从经济增长理论的角度考虑，建立起央行与公众之间的博弈模型，运用双方极值原理求解模型，最终得到最优策略。该策略使得实际GDP水平与期望经济水平尽可能接近的同时，物价水平尽可能低。

1模型建立

微分对策是对策论在动态情况下的发展，欲建立微分对策模型，则需寻找央行与公众间博弈的状态方程与目标泛函[2,3]。

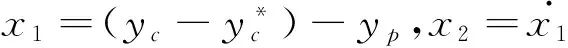
(1)

假设产出水平是由哈罗德-多马模型[4]给出，即生产函数为

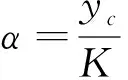
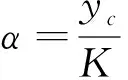
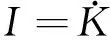
(2)

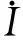
另外由菲利普斯模型[4]，

(3)

其中γ为加权常数，πte为预期期望物价水平增长率。

将式(2)和(3)代入(1)式可得：

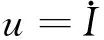
因此该宏观经济博弈微分对策模型的状态方程为

(4)

基于该博弈行为的目标是央行选择u使目标泛函有极小值，公众选择v使目标泛函有极大值，因此可设其目标泛函为

J(u,v)=k[yc(T)-yc*(T)-yp(T)]2+

(5)

式中k为加权常数，T为对策结束的时间。

于是状态方程(4)和目标泛函(5)构成央行与公众宏观金融博弈的微分对策模型。即

(6)

该模型将寻求央行的控制变量u和公众的控制变量v之间满足的关系，使得实际的GDP水平与期望的经济水平在无限接近的同时物价水平也能达到最低。从而关于该模型的求解就变成双方极值问题[2]的求解。

2模型求解

根据式(6)求得央行与公众进行博弈时的控制变量u与v，需运用双方极值原理的Hamilton函数、伴随方程与边界条件[2]。

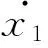
其中t0表示初始时刻，x1(t0)表示初始时刻的实际经济水平和期望水平的差值再与物价水平之差。

记目标泛函J(u,v)的被积函数为

因此该模型的Hamilton函数为

令Ψ=kx12(T)，则伴随方程及边界条件为

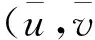
故

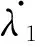
λ1(t)=λ1(T)+2k[x1(t)-x1(T)]

由于λ1(T)=0，故

λ1(t)=2k[x1(t)-x1(T)]

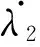
λ2(t)=λ2(T)+2k(t-T)x1(T)

由于λ2(T)=0，故

(7)

其中x1(T)表示博弈结束时刻实际经济水平和期望水平的差值再与物价水平之差。

观察式(7)，欲得到λ2(t)的具体表达式，需要解出x1(T).

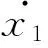
求解得

其中t0表示初始时刻，x2(t0)表示初始时刻的经济增长率与物价增长率之差。

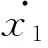
+(T-t0)x2(t0)+x1(t0)，整理得

将其代入λ2(t)=2k(t-T)x1(T)，得

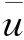
3结论说明

(8)

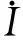
[参考文献]

[1]陈学彬. 金融博弈论[M]. 上海：复旦大学出版社，2007：1-33.

[2]张嗣瀛. 微分对策[M]. 北京：科学出版社，1987：2-20.

[3]张嗣瀛. 关于定量与定性微分对策[J]. 自动化学报，1980,6(2): 121-128.

[4]吴易风，刘凤良，吴汉洪. 西方经济学[M].北京：中国人民大学出版社，1998：526-579.

[5]傅莉，王晓光. 微分对策理论及其研究现状分析[J]. 沈阳航空工业学院学报，2010,27(4)：60-61.

[6]李登峰. 微分对策及其应用[M]. 北京：国防工业出版社，2000：2-52.

[7]Erichson，G.M. Differential game models of advertising competition[J]. European Journal of Operational Research, 1995, 83(3):431-438.

[8]JØrgensen,S. , Sigue, S.P.&Zaccour,G. Stackelberg leadership in a marketing channel[J]. International Game Theory Review, 2001, 3(1):13-26.

责任编辑：王与

中图分类号：K249.3

文献标识码：A

文章编号：1673-1794(2016)02-0016-03

作者简介：程潘红，滁州学院数学与金融学院助教，硕士(安徽 滁州 239000)。

基金项目：滁州学院科研项目(2015Gp6)；安徽省省级教学团队(2014jxtd040,2015JXTD035)；安徽省大学生创新创业训练计划项目(201510377007)

收稿日期：2015-05-23