混合鱼群优化算法的贝叶斯网络结构学习

陈梦洁，万　源，吴克风，童恒庆

(1.武汉理工大学 理学院，湖北 武汉 430070；2.华中科技大学 自动化学院，湖北 武汉 430074)



混合鱼群优化算法的贝叶斯网络结构学习

陈梦洁1，万源1，吴克风2，童恒庆1

(1.武汉理工大学 理学院，湖北 武汉 430070；2.华中科技大学 自动化学院，湖北 武汉 430074)

摘要：针对从数据集学习贝叶斯网络结构准确率不高的问题，提出了一种基于混合鱼群优化算法的结构学习算法。首先，利用互信息和最大似然树生成初始无向图;然后，由无向图的边随机生成初始种群，将粒子群算法的个体记忆和交流意识引入鱼群算法的行为模式，减小算法搜索行为的盲目性;最后，将优势遗传算法的变异和交叉算子应用于算法的寻优过程。仿真实验结果验证了改进后的算法具有更强的寻优能力。

关键词：贝叶斯网络；结构学习；粒子群算法；人工鱼群算法；自适应遗传算法

0引言

贝叶斯网络(Bayesian network，BN)结合了图论和概率论，善于解决不确定性知识的表达和推理问题。BN被广泛应用在人工智能、自动控制和机器学习等领域。BN结构学习的方法[1-4]可分为3类：基于条件独立性测试的方法、基于评分搜索的方法和混合算法。

由于寻找最优贝叶斯网络是一个非确定性多项式(non-deterministic polynomial，NP)难题，网络结构空间大小会随着网络节点个数的增加呈指数增加，因此，BN结构学习的方法主要采用启发式搜索方法。文献[3]将基于免疫策略的二进制粒子群算法应用于BN结构学习，算法收敛较快，但准确度仍待提高。文献[4]提出了基于改进粒子群优化算法的BN结构学习方法，通过节点的互信息限制网络结构的搜索空间，适用于节点较少的网络结构。文献[5]提出了基于进化算法的BN结构学习方法，学习效果较好，但是编码方式较复杂，对计算机性能要求较高，且易陷入局部最优。文献[6]将云自适应遗传算法和鱼群算法混合，用于BN结构学习，可以避免陷入局部最优，但由于寻优过程具有随机性，初始种群的随机性较大，影响了算法的准确度。

基于文献[5-6]的方法，本文根据粒子群算法中粒子对自身经历的最优位置和全局当前最优位置的认知意识，在鱼群算法的“聚群”和“追尾”行为模式中引入“回溯”和“协作”行为，将优势遗传算法的变异和交叉算子应用于鱼个体位置的更新过程，形成改进的混合鱼群优化算法。并将算法应用于BN结构学习中，验证算法的准确性。

1改进的鱼群优化算法

人工鱼群算法[7](artificial fish swarm algorithm，AFSA)通过模拟鱼群的聚群、追尾、觅食以及随机行为构造人工鱼。根据当前所处的环境状态，人工鱼会选择“聚群或觅食”和“追尾或觅食”两种行为模式中更优的一种行为模式来执行，并在公告板上记录最佳位置，当达到最大迭代次数时，人工鱼会聚集在极值周围，从而实现全局最优。

传统鱼群算法的寻优搜索行为具有随机性，“聚群或觅食”和“追尾或觅食”两种行为模式又使得算法搜索行为具有局限性。本文算法根据粒子群算法[8]中粒子对自身经历的最优位置和全局当前最优位置的认知意识，在基本鱼群算法的“聚群”和“追尾”行为模式中加入“回溯”和“协作”行为，扩充鱼群算法的行为模式，使得鱼群行为模式更加全面，增加最优位置产生的概率，减小算法搜索行为的盲目性。觅食行为使得鱼群可以任意游动到新位置，增加了种群的多样性，有利于跳出局部最优。

2基于混合鱼群优化算法的贝叶斯网络结构学习

2.1初始种群的生成

互信息可以反映变量之间的相关关系，互信息越大，表明变量之间的依赖程度越大，变量间存在有向边的可能性就越大[9]。通过变量之间的互信息，可以排除一些不合理的网络结构，从而缩小搜索空间。

其中：I(Xi,Xj)为变量Xi与变量Xj之间的互信息；xm与xn分别为变量Xi与变量Xj的各个取值；P(xm)为变量Xi的概率；P(xn)为变量Xj的概率；P(xm,xn)为变量Xi与变量Xj之间的概率。

采用文献[10]提出的最大生成树法获得无向图，以该无向图为基础生成初始种群。首先，计算出任意两个节点之间的互信息；然后，根据互信息的大小赋予节点之间的边权重；再根据边权重生成最大权重遍历树即最大生成树，使得生成树中所有边的权重之和最大。

由最大生成树即无向图随机生成初始种群个体，故初始种群所对应的网络结构的边只能从这里的无向图中的边随机产生。该无向图的边作为优化最佳贝叶斯网络结构的待选边，减弱了初始种群对算法的影响，算法的收敛速度也有较大的提高。

2.2评分标准

度量网络结构G与样本数据集D匹配程度的函数称作评分函数。贝叶斯信息准则[11](Bayesian information criterion，BIC)是BN结构学习算法常用的评分函数，依照模型的优参对数似然度和模型复杂度的罚项来选择模型，可以避免过度拟合。故采用BIC作为本文算法的适应度函数。

2.3基于自适应遗传算子的鱼群位置更新策略

(1)鱼个体在当前状态X下，当视距范围内伙伴数目n>1且拥挤度m<δ，m是随机产生的随机数，且m∈(0,1)，即保证周围不会过分拥挤的情况下，分别执行聚群、追尾、回溯和协作行为。将遗传算法中常用的单点交叉应用于这4种行为，即选取当前个体与待配对个体进行交叉。若两个个体对应的编码行向量分别为111010101和101010111，随机选取一个交叉位假定为第5位，则交叉后产生的新个体为111010111和101010101。

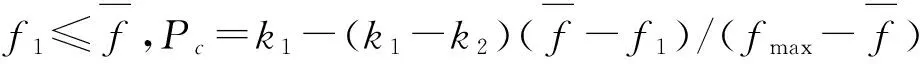
(Ⅱ)否则Pc=k1。

同理，追尾行为是以当前鱼个体X1与视距范围内最优位置的个体Xb交叉；回溯行为是以当前鱼个体X1与自身所经历最优位置的个体Xpb交叉；协作行为则是以当前鱼个体X1与当前迭代过程整个鱼群最优位置的个体Xgb交叉。

交叉率Pc的取值采用优势遗传的思想，使高适应度的个体以较大的交叉率进行有利于优势基因的遗传，与传统的遗传算法相比，优势遗传能够保留精英个体的特性[14]。但为了保护种群多样性，k1值不宜过小，k1值宜设定为0.7～1.0，k2值设定为0.5～0.7。

鱼个体试探进行聚群、追尾、回溯和协作这4种行为后，会分别计算出4种行为所产生个体的新适应度值。采用行为选择策略，根据适应度的优劣，选择最有利的行为并执行。

(2)当n<1或者m≥δ，鱼个体执行觅食行为，将遗传算法的变异算子应用于觅食行为。变异过程是随机选取一个变异位，并对变异位的元素进行由1变0或由0变1的变换。变异过程本质上是对原来的网络结构进行加边、减边和反转边的操作。

(Ⅱ)否则Pm=k4。

变异率Pm的取值表明:在高适应度的个体以较小的变异率进行变异以保留优良个体的同时，低适应度的个体以较高的概率进行变异，增大变异出优势个体的概率，利于优势个体的产生，跳出局部最优。故k3值一般设定为0.4～0.5，k4值一般设定为0.3～0.5。

(3)环路修正

为了保证鱼个体更新位置后对应网络结构的合法性，需要对非法网络结构进行修复。具体步骤如下：

步骤1：根据更新后的网络结构，得到网络结构对应的邻接矩阵。

步骤2：若矩阵对角线上的元素不都为0，说明网络结构存在自循环，将对角线上值为1的元素替换为0，否则，进入步骤3。

步骤3：若矩阵上的元素存在gij=gji=1，则网络结构中存在双向边，任意选择其中一个元素，将其对应的值由1替换为0，否则，进入步骤4。

步骤4：若矩阵上的元素存在类似于gik=gkj=gji=1的结构，说明网络结构存在封闭环路，随机选取闭环内的任意一个节点，求出其在闭环内的所有父节点，并删除父节点指向该节点的边。

2.4算法的具体实现步骤

步骤1：初始化鱼群种群个体数FN、交叉率k1及k2、变异率k3及k4、最大迭代次数limit等参数。

步骤2：利用互信息和最大生成树准则确定初始无向图，在无向图基础上，生成初始种群。

步骤3：计算初始种群的所有个体的BIC得分作为个体极值，并将最大得分值及个体记录在公告板上。

步骤4：While 当前迭代次数≤limit时

fori=1:FN

步骤5：当该编号的鱼个体满足聚群条件时，需执行“聚群”、“追尾”、“回溯”和“协作”这4种行为。

步骤6：判断执行4种行为的新个体是否存在非法结构，若存在，则进行环路修正，否则，保留合法个体。

步骤7：比较4个新个体之间的BIC得分，评定最优行为，执行并记录。

步骤8：当鱼个体不满足聚群条件时，需要执行觅食行为，游到新位置。

end

步骤9：记录当前最优位置，并更新公告板，迭代次数加1。

步骤10：当达到最大迭代次数时，输出最优贝叶斯网络结构及最大得分值。

3仿真实验

选取贝叶斯基准网络Asia和Alarm进行仿真实验，验证本文算法的有效性，实验目的是根据数据集得到最接近标准网络的贝叶斯网络结构。

表1　本文算法与标准网络的BIC评分

分别选取Asia网的1 000组、2 000组、5 000组及10 000组的数据集，并将标准网络和本文算法各运行10次，记录10次实验所得的最小BIC评分值，结果见表1。由表1可知：不管在哪种数据集下，10次实验所得的最小BIC评分值都大于原始结构(标准网络)的BIC评分值，而且随着数据集样本量的增加，得分差距变大，说明本文算法的学习性能较好。

将本文算法与遗传鱼群算法、离散粒子群算法进行比较，验证本文算法在不同数据样本集下的学习效果。分别用3种算法对Alarm网络学习10次，结果见表2。由表2可知：在与标准Alarm网络对比多边、缺失边和反向边的均值时，本文算法学习的网络结构与标准网络结构的差距最小，特别是在10 000组数据集下，差距要明显小于遗传鱼群算法和离散粒子群算法，验证了本文算法的有效性。

表2　3种算法对Alarm网的学习结果(边的数量)

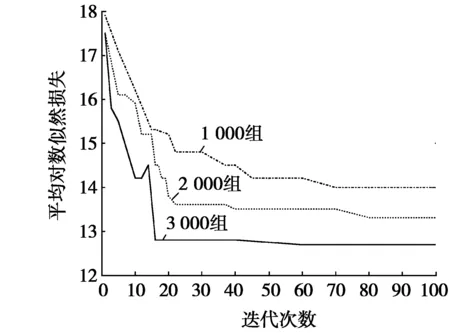
图1　不同样本数据集下的平均对数似然　　　损失比较

4结束语

本文在基本鱼群算法的基础上融入粒子群算法的两个重要特征，增强了算法寻优的目标性，加大了全局搜索的力度，加快了算法收敛。同时采用优势遗传理论，使得优势个体最大限度地被保留，形成改进的混合鱼群优化算法，并应用于贝叶斯网络结构学习。仿真实验结果验证了本文算法具有更强的学习能力和较高的准确性。下一步工作是采取措施降低算法复杂度，在小样本容量的情况下，得到更优的网络结构。

参考文献：

[1]LARRANAGA P,KARSHENAS H,BIELZA C,et al.A review on evolutionary algorithms in Bayesian network learning and inference tasks[J].Information sciences,2013,233(2):109-125.

[2]LI Y Y,YANG Y L,ZHU X F,et al.Towards fast and efficient algorithm for learning Bayesian network[J].Wuhan university journal of natural sciences,2015,20(3):214-220.

[3]LI X L,HE X D.A hybrid particle swarm optimization method for structure learning of probabilistic relational models[J].Information sciences,2014,283:258-266.

[4]高晓光,邸若海,郭志高.基于改进粒子群优化算法的贝叶斯网络结构学习[J].西北工业大学学报,2014(5):749-755.

[5]ZHU Y,LIU D,JIA H.A new evolutionary computation based approach for learning Bayesian network[J].Procedia engineering,2011,15:4026-4030.

[6]郭童,林峰.基于混合遗传鱼群算法的贝叶斯网络结构学习[J].浙江大学学报(工学版),2014,48(1):130-135.

[7]XIAO J,ZHENG X,WANG X,et al.A modified artificial fish-swarm algorithm[C]// Intelligent Control and Automation,2006.WCICA 2006.The Sixth World Congress on IEEE,2006:3456-3460.

[8]段其昌,唐若笠,徐宏英,等.粒子群优化鱼群算法仿真分析[J].控制与决策,2013,28(9):1436-1440.

[9]刘乐乐,田卫东.基于属性互信息熵的量化关联规则挖掘[J].计算机工程,2009,35(14):38-40.

[10]CHOW C,LIU C.Approximation diserete probability distributions with dependence trees[J].IEEE transactions on information theory,1968,14(3):462-467.

[11]DALY R,SHEN Q,AITKEN S.Learning Bayesian networks:approaches and issues[J].Knowledge engineering review,2011,26(2):99-157.

[12]LARRANAGA P,POZA M,YURRAMENDI Y,et al.Structure learning of Bayesian networks by genetic algorithms:a performance analysis of control parameters[J].IEEE transactions on pattern analysis & machine intelligence,1996,18(9):912-926.

[13]赵斌,宿玉佩,蒋念平.一种改进型遗传算法的网格工作流调度研究[J].河南科技大学学报(自然科学版),2012,33(3):32-35.

[14]陈世哲,刘国栋,浦欣,等.基于优势遗传的自适应遗传算法[J].哈尔滨工业大学学报,2007,39(7):1021-1024.

[15]FRIEDMAN N.Learning belief networks in the presence of missing values and hidden variables[C]// Proceedings of the Fourteenth International Conference on Machine Learning.2000:125-133.

基金项目：国家自然科学基金项目(91324201,81271513)

作者简介：陈梦洁(1990-),女,河南信阳人,硕士生;万源(1976-),女,湖北武汉人,副教授,博士,硕士生导师,主要研究方向为机器学习与数据挖掘.

收稿日期：2016-01-05

文章编号：1672-6871(2016)04-0041-05

DOI:10.15926/j.cnki.issn1672-6871.2016.04.009

中图分类号：TP391

文献标志码：A