基于多标签数据的降维与分类算法的研究

汤文伟，于威威（上海海事大学，上海　201306）



基于多标签数据的降维与分类算法的研究

汤文伟，于威威
（上海海事大学，上海201306）

摘要：

关键词：

0　引言

在传统的数据分类中，我们一般把数据标注为单一的类别标签。但是在实际的生活应用中，一个数据通常可以同时被标注为多个标签。例如，我们经常会看到一些非常美丽的照片或者是风景图片，在这些图片上往往会有山有水还有人物；很多影视作品，我们在其描述信息中会看到上映时间、作品类型、出品公司等信息；还有一些新闻性质的报导，我们可以把其标注为国家、实事、政治、经济等。这类数据统称为多标签数据[1]。多标签数据的分类就是针对给出的数据的特点，得到其对应的数据模型，最终要实现的就是依据此数据模型来判断未知类别的过程[2]。与我们熟悉的单标签数据分类最大的不同就是，多标签分类最终会输出多个结果。多标签数据的分类在我们的现实生活中应用已经很广泛了，如定基因功能分类[3]、定向营销[4]、图像语义注释[5]等。

目前，已经有一些多标签分类的学习算法，我们可以把这些算法大致分为两类，即问题转化方法和自适应方法。问题转化方法实质上就是把多标签分类的问题转化为传统单标签分类问题，然后应用已有的单标签分类方法进行数据的分类。该方法的主要转化策略有选择、标签幂集、忽略、二元相关和复制等。另一种就是算法自适应方法，即在传统分类算法的基础上设置不同的约束条件，使其能直接处理多标签数据，将其进行准确的分类。该方法的典型代表有支持向量机[6]、C4.5[6]和BP-MLL[7]等。

多标签数据分类无疑能使我们将数据进行更详细更完整的分类，但随着新的分类技术的出现，多标签数据正在面临着高维度的问题。数据的高维性是一把双刃剑，它一方面可以为分类模型的建立提供充足的分类信息，但另一方面也给分类算法带来了许多弊端，如峰值问题、过拟合和维度灾难等。所谓的峰值问题是指分类的性能刚开始时会随着维数的增加而不断提高，但当到达一定程度后，其性能会随着维数的增加而降低；这里的维度灾难简而言之就是随着数据维度的不断增加，进行分类时所需要的训练样本数量将呈指数的形式增加。正是由于维数的双面性，我们需要对维数进行约减，这里我们使用特征选择的方式，特征选择是一种有效的维数约减的技术，所谓的特征选择就是根据某种评估标准从原始的特征空间中选择一个最优的特征子集来代替原来的特征空间，以此来构建分类模型的过程。由于在进行特征选择时是根据所选定的评估标准进行的，所以评估标准在特征选择过程中起着决定性的作用，其选择的好坏将直接决定特征选择算法性能及最终分类模型的分类效果。到目前为止，已经存在了很多评估标准，如信息准则、一致性准则、距离准则和分类误差准则等。

1　条件互信息

现有的基于互信息的多标签特征选择的方法可以有效地减少多标签数据的维度。例如，Lee和Kim[8]提出一种基于多元互信息的多标签特征选择方法，通过选择一个有效的特征子集来最大化所选特征与标签之间的依赖。同时，Lee和Kim[9]提供了一个利用互信息进行多标签特征选择的算法。这个算法可以测量变量之间的依赖关系。此外，Lee和Kim[10]还提出一种迷因多标签特征选择方法，该方法通过重新定义特征来发现遗传搜索子集。除此以外，Doquire和Verleysen[11]也设计了一种针对多标签问题的基于互信息的特征选择算法，该算法首先利用PPT转换问题，然后使用基于互信息的贪婪搜索策略来选择与分类最相关的特征。

虽然以上方法在多标签的特征选择方面起到了一定的效果，但未涉及到对于减少冗余特征的选择方法。在多标签学习中，冗余不仅仅包括候选特征和使选特征之间的互信息，还包括当所有选特征已给定时候选特征之间的互信息。在本文中提出一种基于最大依赖和最小冗余的多标签特征选择的方法来提高特征在多标签学习性能方面的能力。

1.1熵与互信息

香农熵[12]是一个不确定的随机的变量，并广泛应用于不同的领域。若A=｛a1，a2，a3，…，an｝是一个随机变量，P（ai）是ai出现的概率。

那么A的熵可以被定义成：

如果B=｛b1，b2，b3，…，bm｝是一个随机变量，A和B的联合概率表示为p（ai，bi）。

那么A和B的熵可以被定义成：

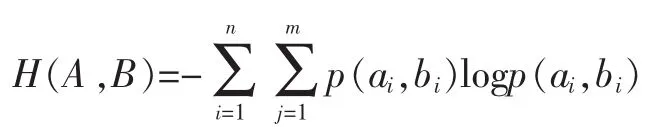
假设A是已知的，那么B的熵的值则被定义为条件熵：

证明：

当A的熵减小后观察B，我们会发现B的熵值也在变化，这就是A与B之间的互信息，被定义为：

互信息可以反映A与B之间统计关系之间的程度，我们有：

证明：

1.2基于最小冗余和最大依赖的特征选择

特征选择的目标就是选择一个能最大化保持原始特征空间的紧凑的特征子集。基于信息理论，Bell和Wang[13]介绍了第一个公理化特征子集的选择方法。

公理1：（学习信息的保存）给定一个数据集，其特征集为F标签集为C，预期的特征子集为S，若S满足MI（S；C）=MI（F；C），则保存此特征子集S。

公理2：（最小的编码长度）[14]给定一个数据集，其特征集为F标签集为C，S是其一个特征子集。若存在S1∈S使得联合熵H（S1，C）最小，则S1可以作为标签判断的依据。

公理1和公理2给出了基于互信息的理论，一个好的特征子集需要具备的一些条件。不同于单标签学习，多标签分类中标签是一个标签的集合。

接下来提出一种新的针对多标签学习的公理化方法。

公理3：（多标签学习信息的保存）[15]给定一个数据集，其特征空间为F，标签的空间为L，预期的特征子集为S，若S满足MI（S；L）=MI（F；L），则S可以作为多标签学习的特征子集。

公理4：（多标签学习的最小编码长度）

通过（1）我们可以得出以下属性：

属性1：如果待选的特征f+和每一类标签li∈L是相互独立的，那么f+和L之间的互信息[15]是最小的。

属性2：如果每一类的标签li∈L完全是由f+决定的，那么f+和L之间的互信息是最大的。

从属性1和属性2，我们可以使用公式（1）来选择与所有类标签有着最大依赖的特征。然而基于最大依赖的特征可能会产生冗余。因此当我们在特征选择[16]时要衡量特征之间的冗余。不同于传统的单标签特征的选择，在多标签特征的选择过程中不仅要考虑每个特征之间的冗余，还要考虑每个类标签与特征之间[17]的最大依赖性。假设S为一个已选定的特征子集。则最小冗余可以用以下公式来衡量：

将式（3）进行转化：

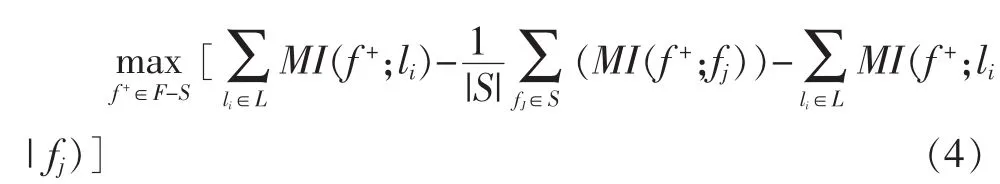
我们可以继续对式（4）进行变换：

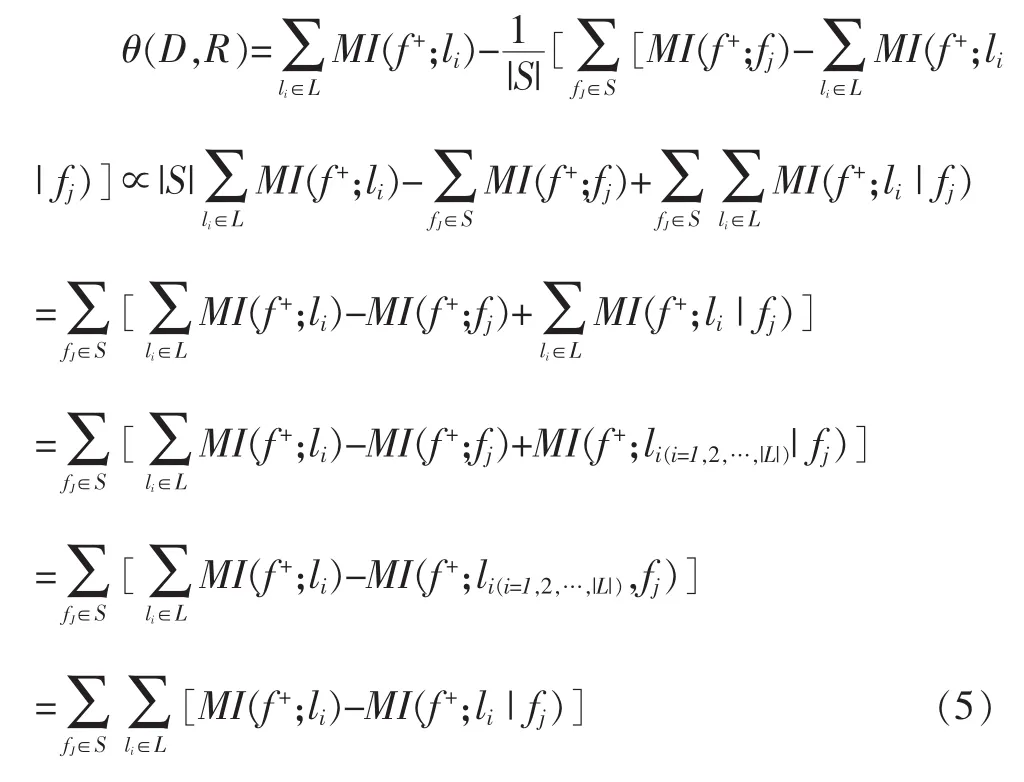
从（5）中我们可以更清晰地看出特征与标签的最小冗余和最大依赖的关系了。

接下来就介绍一下基于最小冗余和最大依赖的多标签特征选择算法的基本步骤：

算法步骤：

输入：N：被选择特征的数目。

输出：S：特征的排名。

①初始化S=Ø，F=｛f1，f2，…，fN｝；

②判断|S|＜N，若不等式成立则执行③，否则退出；

③寻找f∈F，能使得（8）中的值最小；

④S=S∪｛f｝；

⑤F=F-｛f｝；

⑥返回S；

2　基于改进的KNN分类算法

在本文的第二节着重介绍了一下在进行多标签数据分类之前所进行的特征选择，这将大大提高我们多标签分类的效率。当特征选择完成之后，选择什么样的分类算法对分类的结果将有着至关重要的影响，在本节中我们将介绍一种改进的KNN算法。

算法步骤：

输入1：多标签训练样本集｛（Χi，Yi），i＝1，2，…，m｝，其中X=｛Χ1，Χ2，…，Χm｝，Χi∈X，Y=｛λ1，λ2，…，λn｝，Yi⊆Y。

输入2：多标签测试样本集｛Χm+1，Χm+2，…，Χm+n｝。

输出：图片所属类型。

①通过构造超球（以标签（λ1，λ2，λ3）作为球心来构造超球），然后通过K近邻算法来判断每个超球[20]里面所包含的样本，以欧氏距离作为判断样本是否属于此类标签的依据，K值的确定可以通过不断训练以找到最佳的K值；

②根据第一步得到的超球来构建一个二维数组（以Scene数据集为例，横轴代表样本，纵轴代表标签）：

每个元素代表该样本是否具有该标签，若该样本具有该标签则将赋值为1，否则赋值为0；

③根据②中得到的二维矩阵进行纵向迭代，使其转换为一组一维数组Χi[λ1，λ2，λ3]，由于选择的数据库是scene，所以得到的标签值一共有64种情况，用算法在将其转换为一个具体的数值（就是二进制与十进制的转换）；

④前三步为训练的过程，根据训练的结果将训练的样本进行归类。最后选取测试样本进行测试，方法同上，可以得到测试样本的一个具体标签值，然后根据所得到的标签值进行分类。

3　实验结果与分析

为了验证我们所提出方法的有效性，我们选择了scene数据集作为我们的测试数据集，并且与一些现有的多标签分类算法进行比较。本节首先简要描述多标签数据集和实验的设置，以及给出四个评价标准。然后对实验结果进行评价标准的讨论。

3.1实验基本设置

对于本次实验我们选择了Scene数据集作为测试数据集，以下是Scene数据集的基本信息。

表1　

我们分别采用最小冗余和最大依赖（MDMR）、MLNB、PMU、MDDMspc、MDDMproj四种特征选择方法对特征进行选择，然后在利用我们改进的KNN算法（K取值10）对图像进行多标签分类。

3.2评价标准

由于多标签数据分类输出的结果往往是多标签的，那些基于单标签的评价标准[24]（如查全率、查准率等）已无法满足。因此，在本文中利用新的适合于多标签分类[25]的四个评价标准。

（1）汉明损失（Hamming Loss）

汉明损失[26]是用来量化基于单个标签的分类误差，简而言之，就是本该属于该样本的标签没有出现在该类标签的集合，而相反不属于的却出现在集合中了。该值越小，说明分类性能越好。其定义是：

其中，Δ指的是对称差算子[27]，表示两个集合的对称差只属于一个集合而不是属于另一个集合的元素组成的集合。

（2）Coverage

Coverage指的是所选特征子集的覆盖范围[28]。

（3）排序损失（Ranking Loss）

排序损失指的是所有标签的出错程度[25]，该值越小，性能越优。

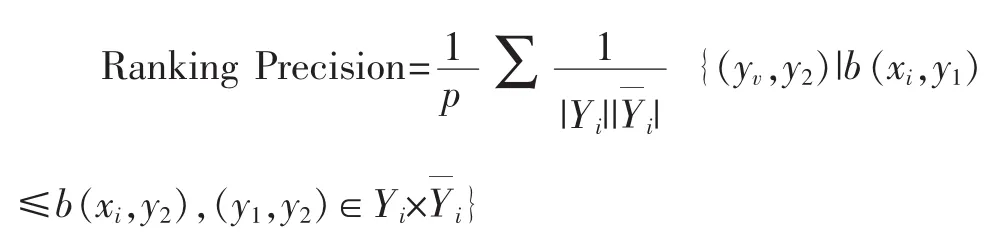
（4）平均精度（Average Precision）

平均精度表示的是分类模型标签预测准确程度[29]。该指标越大则分类模型性能越优。

3.3实验结果

根据3.2中的评价标准，我们可以得出针对Scene数据集在不同多标签分类算法下的分类效率。

各方法性能的比较如下表：

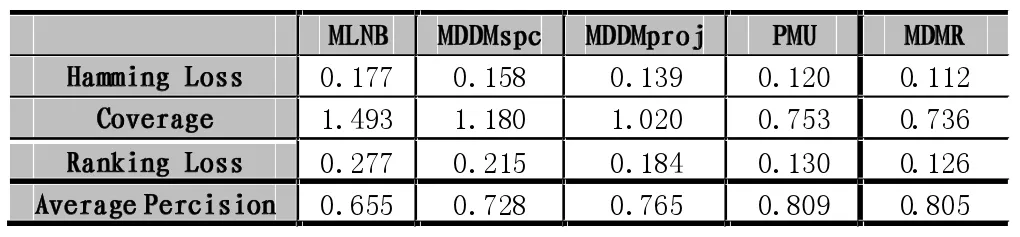
表2　

3.4结果分析

先对Scene数据集利用MDMR算法对特征进行选择，然后使用本文提出的改进的KNN算法对图像进行分类，通过上述实验数据可以看出对比于其他多标签分类算法（MLMB[30]、MDDMspc[31]、MDDMporj[32]、PMU[33]），在Hamming Loss、Coverage、Ranking Loss、Average Percision四个分类评价标准中，MDMR都有着明显的优势。

不同于传统的单标签数据的分类，标签之间的相互依赖[34]是多标签分类中的一个重要的特点。因此解决多标签特征选择的问题对于多标签分类的效率有着至关重要的影响。

从以上实验数据我们可以清晰地看到不同的多标签特征选择方法可以减少多标签数据的维数，从而提高多标签分类的效率。在本文中我们确定两个重要的因素来衡量特征，即依赖和冗余。我们采取最大依赖和最小冗余的特征选择策率对特征集进行选择。最终，实验结果表明我们给出的方法与现有的一些方法更加有效。

图1　

参考文献：

[1]Tsoumakas G，Katakis I.Mutilabel Classification：An Overview[J].Data Warehousing and Mining，2007，3（3）：1-13.

[2]Tsoumakes G，Katakis I，Vlahavas I.Mining Multilabel Data[M].Data Mining and Knowledge Discovery Handbook.New York：Springer，2010.

[3]Boutell M R，Luo Jie-Bo，Shen Xi-Peng，Et Al.Learning Multilabel Scene Classification[J].Pattern Recognition，2004，37（9）：1757-1771.

[4]Zhang Yi，Burer S，Street W N.Ensemble Pruning Via Semidefinite Programming[J].Machine Learning Research，2006，7（12）：1315-1338.

[5]Blockeel H，Schietgat L，Struyf J，et al.Decision Trees for Hierarchical Mulilabel Classification：A Cass Study in Functional Genomics[M].New York：Spring Berlin Heidelberg，2006.

[6]Tsoumakas G，Vlahavas I.Random K-Labelsets：An Ensemble Method for Multilabel Classification：Machine Learning[M].New York：Spring Berlin Heidelberg，2007.

[7]Zhang Min-Ling，Zhou Zhi-Hua.Mutilabel Neural Networks with Application to Functional Genomics and Text Categorization[J].IEEE Transactions On Knowledge And Data Engineering，2006，18（10）：1338-1351.

[8]J.Lee，D.Kim，Feature Selection for Multi-Label Classification Using Multivariate Mutual Information，Pattern Recognit.Lett.34（2013）349-359.

[9]J.Lee，D.Kim，Mutual Information-Based Multi-Label Feature Selection Using Interaction Information，Expert Syst.Appl.42（2015）2013-2025

[10]J.Lee，D.Kim，Memetic Feature Selection Algorithm for Multi-Label Classification，Inf.Sci.293（2015）80-96.

[11]G.Doquire，M.Verleysen，Mutual Information-Based Feature Selection for Multilabel Classification，Neurocompution，122（2013）：148-155.

[12]C.Shannon，A Mathematical Theory Of Communication，Bell Syst.Tech.J.27（1948）：379-423，623-656.

[13]D.Bell，H.Wang，A Formalism For Relevance and Its Application In Feature Subset Selection，Mach.Learn.41（2000）：175-195.

[14]LEWIS D D，YANG Y，ROSE T G，et al.Rcvl：A New Benchmark Collection for Text Categorization Research[J].The Journal of Machine Learning Research，2004（5）：361-397.

[15]ZHANG M L，ZHOU Z H.Multilabel Nerural Networks with Applications to Functional Genomics and Text Categorization[J].IEEE Transzction on Knowledge and Data Engineering，2006，18（10）：1338-1351.

[16]汤进，黄莉莉，赵海峰，等.使用D适应线性回归多标签分类算法[J].华南理工大学学报（自然科学版），2012，40（9）：69-74.

[17]王国强.Rough集理论与知识获取[M].西安：西安交通大学出版社，2001.

[18]张玲.问题求解理论及应用[M].北京：清华大学出版社，1990.

[19]D.Zhou，J.Huang，B.Scholkopf，Learning Form Labeled and Unlabeled Data on Adirected Graph[C].Proc.22 Nd Int'l Conf.Machine Learning，2005，1041-1048.

[20]Szummer，M.Jaakkola，T.Partially Labeled Classification With Markov Random Walks[C].Advances in Neural Information Procession Systems（NIPS），2001，14：1-8.

[21]Leo Grady，Random Walks for Image Segmentation[C].IEEE Transcation on Pattern Analysis and Machine Intelligence.，2006，28（11）：1768-1783.

[22]C.Ding，Spectral Clutering[C].Tutorial Presented at the 16th European Conf.Machine Learning（Ecml），2005.

[23]Tang L，Rajan S，Narayanan V.Large Scale Multi-Label Classification Via Metalabel[C].Proceedings of the 18th International World Wide Web Conference.Madrid：Acm，2009：211-220.

[24]Fan R，Lin C.A Study on Threshold Selection For Multi-Label Classification[R].Taiwan：Department of Computer Science，National Taiwan University.2007：1-23.

[25]郑伟，王朝坤，刘璋，王建民.一种基于随机游走模型的多标签分类算法.计算机学报，2010，33（8）：1418-1426.

[26]张敏灵.一种新型多标签懒惰学习算法[J].计算机研究与发展，2012，49（11）：2271-2282.

[27]张贤达.矩阵分析（M）.1版.北京：清华大学出版社，2008.

[28]王国胤，张清华，胡军.粒计算研究综述[J].智能系统学报，2007，2（6）：8-26.

[29]Jain A.K，Murty M.N，Flynn P.J.Data Clustering；A Review[J].ACM Compution Surveysm，1999，31（3）：264-323.

[30]Weiwei Cheng，Eyke Hullermeier.Combining Instance-Based Learning And Logistic Regession for Multilabel Classification[J].Machine Learning.Volume 76 Number 2-3，211-255.

[31]Huawen Liu，Shichao Zhang.Noisy Data Elimination Using Mutual K-Nearest Neighbor for Classification Mining[J].The Journal of System And Software 2012，85：1067-1074.

[32]J.Read，B.Pfahringer，G Holmes，et al.Classifier Chains for Multi-Label Classification[J].Lecture Notes in Artificial Intelligence 5782，2009：254-269.

[33]Weizorkowska A，Synak P，et al.Multi-Label Classification of Emotion in Music[J].Advances in Soft Computing，2006，Volume 35/ 2006，307-315.

[34]Furnkranz J，Hollermeier E，et al.Multilabel Classification Via Calibrated Label Ranking[J].Machine Learning，2008，72（2）：133-153.

Research on Dimension Reduction and Classification Algorithm Based on Multi Label Data

TANG Wen-wei，YU Wei-wei
（Shanghai Maritime Univeristy，Shanghai 201306）

Abstract：

Now，is well known that the classification of a single label，the traditional method of supervised learning are used in data in a single label，but the increasing rich data，single-label can no longer complete description of a sample of the information，a sample often can corresponds more tags todays，so multi-label classification data gradually become an important research direction of data mining.While many labels to better information to describe a sample，multi-label data is usually characterized by a large number of the kind of data，so it is difficult to process such data directly，and these high-dimensional data while there is often the curse of dimensionality problem，Data before doing so multi-label data classification dimension reduction on the final classification and plays an essential role.Presents for this condition based on the use of mutual information（Minimum Redundancy AND Maximum Dependent）to select the feature set，removing useless features information，and then through an improved KNN algorithm for data classification，experimental results show that this method is that the average recall rate increased by 2.5％.

Keywords：

现在为人们所熟知的是单标签的分类，传统的监督学习的方法主要应用在单标签的数据中，但随着数据的日益丰富，单标签已经不能再完整地描述一个样本的信息，现在往往一条样本会对应多个标签，所以多标签数据的分类逐渐的成为数据挖掘的一个重要研究方向。虽然多标签能够更好地去描述一个样本的信息，但多标签数据通常是那种特征数目很大的数据，对这样的数据直接进行处理很困难，同时这些高维数据往往存在维度灾难的问题，所以对多标签数据进行分类之前做好数据的降维对最终的分类起着不可忽视的作用。提出一种基于采用条件互信息（最小冗余最大依赖准则，MDMR）来进行特征集的选择，去除无用的特征信息，然后通过一种改进的KNN算法对数据进行分类，实验表明这种方法使平均查全率提高2.5％。

单标签；多标签；条件互信息；特征提取；KNN算法

文章编号：1007-1423（2016）14-0003-07

DOI：10.3969/j.issn.1007-1423.2016.14.001

作者简介：

汤文伟（1990-），男，江苏常州人，硕士，研究方向为图像处理、模式识别

收稿日期：2016-03-08修稿日期：2016-05-20

Single-Label；Multi-Label；Conditional Mutual Information；Feature Extraction；KNN Algorithm