主成分分析在计算机模块教学评价中的应用
郝佳睿(广东食品药品职业学院,广州 510520)
主成分分析在计算机模块教学评价中的应用
郝佳睿
(广东食品药品职业学院,广州510520)
摘要:
关键词:
0 引言
考试是教学工作中的一个重要环节,也是衡量学生学习水平和教师教学水平的重要手段和方法。但目前大部分教师对学生考试成绩缺少认真的研究,考试成绩上报教务处系统就等于考试工作的结束,没有进行或只是粗略地进行考试分析,而未真正进行客观的分析和评价。针对这种情况,我们尝试对学院《计算机应用基础》期末考试结果进行定量分析,从分析中获得可靠的反馈信息。
《计算机应用基础》考试内容主要有以下六个模块:计算机基础知识、中文Windows 7操作系统、Word2010文字处理软件、Excel2010电子表格软件、PowerPoint2010演示文稿软件、网络基础与Internet应用等内容。鉴于计算机教学的模块化特点,我们在进行成绩分析的时候不仅要考虑总评成绩,还要考虑到各模块得分的情况。而各个模块之间又有一定量的联系,模块之间有或多或少的相同知识点,如:Word和Excel中文字的编辑、格式设置、文件的保存等都大致相同。所以我们在进行成绩分析时不仅仅要考虑各模块的得分对总评的贡献情况,还要考虑到各模块之间的相关程度。因此本文中利用主成分分析法将六个相互关联的模块转换为2个互不相关的主要成分(主要成分对总评成绩的贡献率达到86%),并得到了各个模块在主成分中所占的比重,进而按照主成分分析方法对成绩进行综合排名。
1 主成分分析法的原理
主成分的基本思想:将原来p个具有一定相关性的指标重新组合成一组新的互相无关的综合指标来代替原来的指标。也即是将原来相关的p个指标的线性组合作为新的综合指标。使新的指标尽可能多地包含原来指标的信息。具体做法如下:
首先,选取原指标的一个线性组合记为F1,即第一个综合指标,使Var(F1)达到最大(Var(F1)越大,说明F1包含的综合信息越多),则F1称为第一主成分。如果第一主成分包含的原信息量没有达到一定的要求(一般要求累计贡献率达到80%以上),再选取原指标的第二个线性组合来有效地反映原信息,记为F2,要求:F1中已有的信息将不出现在F2中,也即要求Var(F1,F2)=0,将F2称为第二主成分。以此类推,可以构造出第三主成分,…,第p个主成分。主成分的线性变换为:其中A=(aij)pp=(a1,a2,…,ap),Rai=λiai,为相关系数
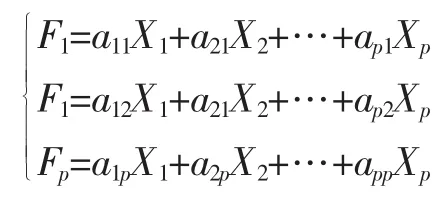
矩阵,a1i,a2i,…,api(i=1,2,…,p)为X的协方差阵的特征根λi(i=1,2,…,p)所对应的特征向量,λ1≥λ2≥…λp≥0。
2 主成分分析的实例
以广东食品药品职业学院2014级《计算机应用基础》期末考试成绩为例,运用主成分分析法对24位任课教师教学能力进行评价。现将任课教师所教56个教学班级的学生成绩总分和各个模块的得分进行平均计算,得到24名任课教师所教班级的平均分,如表1所示:

表1 各教师教学成绩
记:x1:计算机基础成绩,x2:Windows成绩,x3:Word成绩,x4:Excel成绩,x5:网络成绩,x6:PowerPoint成绩。
由于各个模块的分值在总分中所占的比例不同,我们首先对数据进行标准化,使数据量纲相同,以便于较准确地进行分析。标准化后的数据如表2所示。

表2 标准化成绩
通过主成分分析得到标准化后数据各变量之间的相关系数矩阵,如表3所示。可以看出Word和Excel之间的相关性最高,为0.985,这与实际情况也是相符合的,因为Word和Excel中有很多相似的知识,如新建文件、文件复制保存、文档的编辑等。同时,Word和网络、Excel和网络、Windows操作系统和Word、Excel之间也有较高的相关性,说明它们之间有较多类似的知识点。而基础知识和各模块之间的相关程度差距不大,这与基础知识综合考查各模块理论知识是相符的。
表4中为主成分分析得到的数据的特征根和主成分Fi(i=1,2…,6)的方差,以及Fi(i=1,2…,6)的累积贡献率。在主成分的提取原则上,通常提取特征值大于1的前m个主成分且使选取的主成分的累积贡献率达到80%以上,如果特征值小于1则说明该主成分对信息的解释力度较小,还不如直接引入一个原变量的解释力度大。如果累积贡献率小于80%则提取的主成分又不足以包含原变量的信息。在计算机成绩分析中前两个特征根均大于1,λ1=4.163,λ2=1.002,且累积贡献率为86.076%,故选取前两个主成分F1,F2。
表5为初始因子载荷矩阵,每一个载荷量表示主成分与对应变量的相关系数。从中可知:Windows操作系统、Word、Excel、PowerPoint、网络在第一主成分上有较高的载荷,说明第一主成分基本反映了这些模块的信息;基础知识在第二主成分上有较高的成分,说明第二主成分基本包含了基础知识的信息。所提取的两个主成分可以基本反映全部指标的信息。所以我们用两个新的变量来代替原来的变量。并且第一主成分是操作部分的反映,第二主成分是基础知识的反映,符合实际情况。
以表5中第一主成分与原各变量的相关系数(表5中第一列数据)除以第一特征根的平方根(即)(λ1=4.163)),可以得到第一特征根所对应的特征向量(即第一主成分与原变量间的线性系数)。以第二主成分与原标准化变量的相关系数(表5种第二列数据)除以第二特征根的平方根(即:)=1.002)),可得到第二特征根所对应的特征向量(即第二主成分与原标准化变量的线性系数)。由此可以得到:
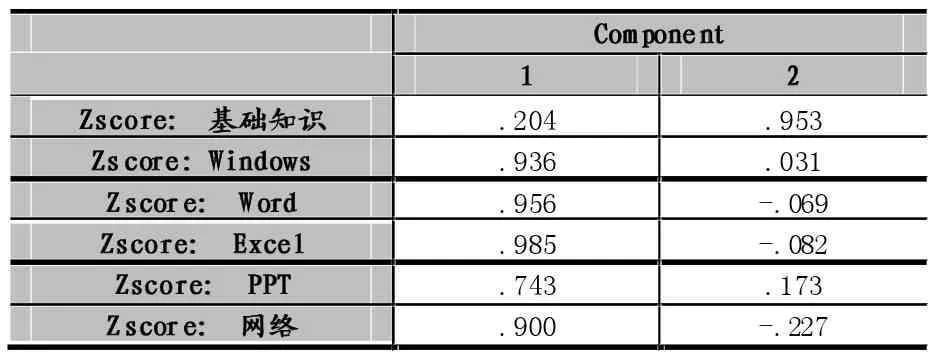
表5 初始因子载荷矩阵

表3 各模块之间的相关系数矩阵
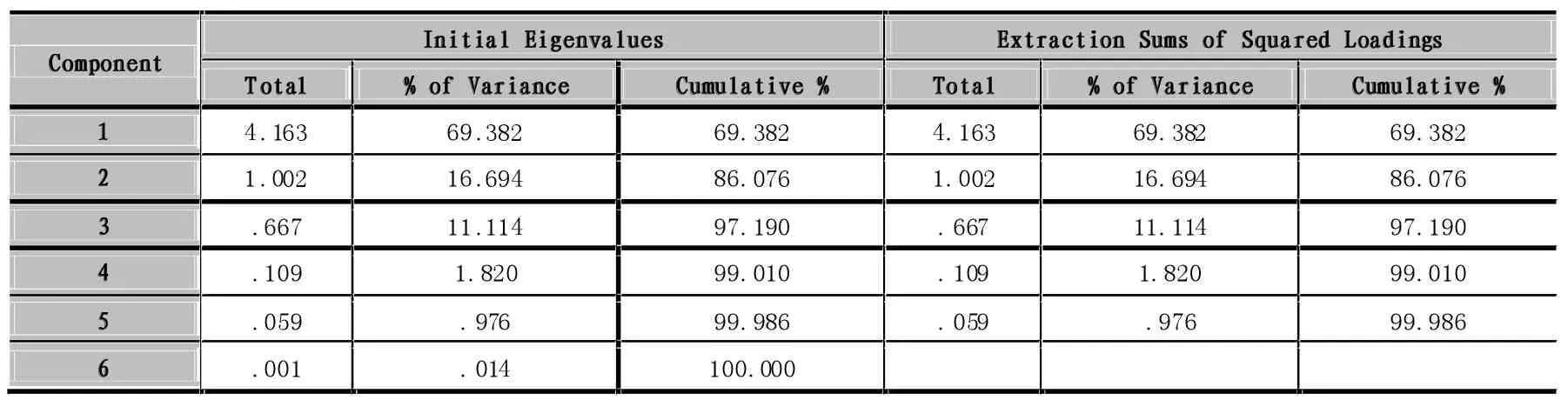
表4 方差分解主成分提取分析表
F1=0.1000ZX1+0.4587ZX2+0.4685ZX3+0.4828ZX4+ 0.3642ZX5+0.4411ZX6
F2=0.9520ZX1+0.0310ZX2-0.0689ZX3-0.0819ZX4+ 0.1728ZX5-0.2268ZX6
分别计算第一、二特征根在所提取的所有特征根和中所占的比例:r1=λ1/(λ1+λ2)=0.806,r1=λ1/(λ1+λ2)= 0.194,进而可得到主成分对原标准化变量的综合线性模型:
F =0.2653ZX1+0.3758ZX2+0.3643ZX3+0.3732X4+ 0.3270ZX5+0.3115ZX6
从模型中可以看出基础知识模块在总评成绩中所占的比重较小,这与基础知识模块得分率比其他模块得分率较低相符。
根据主成分线性模型计算各教师所教班级的教学成绩的主成分值,并对其进行排名比较,即可得到各教师的综合评价比较,见表6。从中可以看到:利用主成分进行综合比较与按照平均分进行比较得到的结果基本一致,最多相差两个名次,这可以从实际数据中得到原因,如教师18,如果按照平均分进行排名是第一位,而按照主成分分析则为第三位,这是由于教师18的总成绩与教师6的总成绩本来就相差较小。教师18的基础知识成绩与教师6的基础知识成绩的差距大于其他模块的平均差距,而基础知识主要体现在第二主成分中,其他模块主要体现在第一主成分中,但第二主成分在总评中所占的比重较小,第一主成分所占的比重较大,所以按主成分分析教师18位次低于教师6。其他的差异也可以从原数据中找到原因。
3 结语
教学评价是研究教师的教和学生的学的价值的过程,目的是为了检查教师教学效果,了解学生学习成绩,为教学改革提供依据,以进一步提高教学质量,促进教学目标的实现。本文应用多元统计中的主成分分析法对学生期末考试成绩的原始数据进行分析处理,得到教师教学成绩综合排名,为教学研究和综合量化管理提供科学的依据。
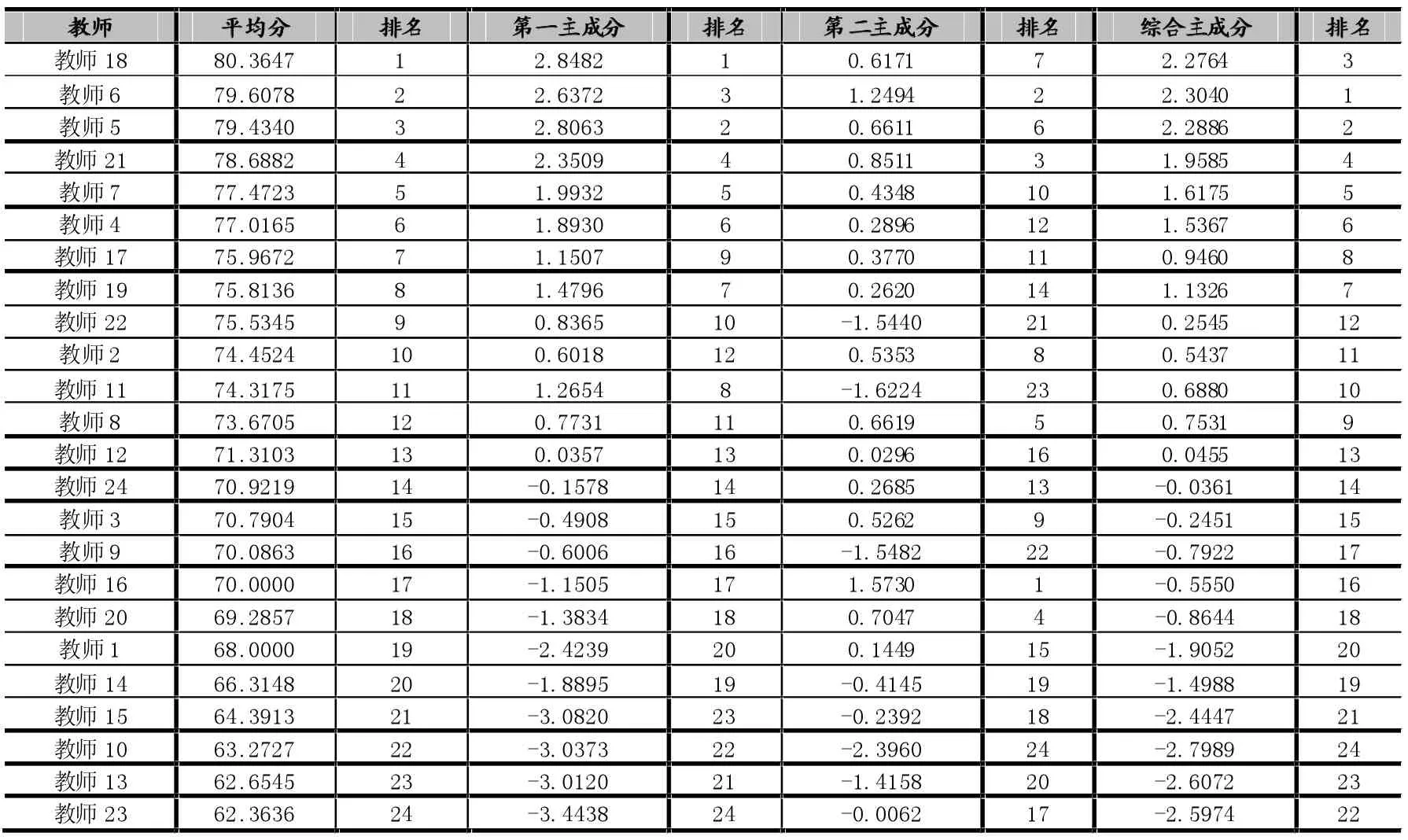
表6 各教师教学成绩的综合比较
参考文献:
[1]张文霖.主成分分析在SPSS中的操作应用[J].理论与方法,2005(12):31-34.
[2]扬宇音,赵雅明,曲立敏.因子分析法在大学生综合排名中的应用[J].贵州工业大学学报,2005,34(1):9~12.
[3]高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005.
[4]何晓群.多元统计分析[M].北京:中国人民大学出版社,2004:143-146.
[5王学民.应用多元分析[M].上海:上海财经大学出版社,2004:236-237.
[6]宇传华.SPSS与统计分析[M].北京:电子工业出版社,2007.
[7]范贺方,樊顺厚等.主成分分析法在学生成绩分析中的应用[J].理论前沿,2009(34):79-80
[8]张绍璞.基于主成分分析中的几类问题的计算公式及结论.天津科技大学学报,2010(4),25(2):76-78.
[9]周春生.主成分分析在大学生成绩影响因素研究中的应用[J].现代计算机,2013(6):12-14.
郝佳睿(1988-),男,软件设计师,硕士,从事领域为计算机教学及计算机应用
The Usage of Principal Component Analysis in Computer Module Teaching Evaluation
HAO Jia-rui
(Guangdong Food and Drug Vocational College,Guangzhou 510520)
Abstract:
The Computer Application Foundation as a compulsory course for students majoring in non- computer,its teaching content mainly has six modules.The characteristics of the modular teaching for computer,tries to use the method of principal component analysis to comparative analyze the final exam,puts forward the main factors that influence the general performance,and the evaluation method of how various impact factors contribute to the general performance.Ranking the teaching effect and comparing the average score are almost the same effect.
Keywords:
《计算机应用基础》作为一门非计算机专业学生的必修课,其教学内容主要有六个模块。针对计算机模块化教学的特点,尝试采用主成分分析的方法对期末考试成绩进行对比分析,提出对总评成绩的主要影响因子,以各影响因子对总成绩贡献的大小为评判方法,对教师的教学效果进行排名,并与按平均分进行排名对比,效果基本一致。
主成分分析;计算机模块;影响因子;累计贡献率
基金项目:
广东食品药品职业学院基金项目(No.2012YR001)
文章编号:1007-1423(2016)14-0064-05
DOI:10.3969/j.issn.1007-1423.2016.14.014
作者简介:book=68,ebook=69
收稿日期:2016-03-10修稿日期:2016-04-15
Principal Component Analysis;Computer Module;Impact Factor;Cumulative Contribution Rate

