一种改进的粒子群优化无线传感器网络定位算法*

张先超　刘兴长

(后勤工程学院后勤信息与军事物流工程系　重庆　401311)



一种改进的粒子群优化无线传感器网络定位算法*

张先超刘兴长

(后勤工程学院后勤信息与军事物流工程系重庆401311)

摘要实现节点的精确定位是无线传感器网络研究领域中一个重要方向。基于粒子群优化的无线传感器网络定位算法与极大似然估计算法、最小二乘法等传统算法相比,定位精度更高,但易陷入局部最优。针对上述缺点,将一种带有动态扰动项的改进算法引入无线传感器网络定位,并在目标函数中引入加权因子,以削弱测距误差的影响。仿真结果表明,该算法可以加快收敛速度,提高定位精度。

关键词无线传感器网络; 粒子群优化算法; 动态扰动项; 定位精度

Class NumberTP393

1引言

无线传感器网络是由随机部署在目标区域内的数量巨大的离散传感器节点组成,节点将采集到的信息以自组多跳的方式传送到基站,从而实现了物理世界和人类社会之间的信息交换[1～2]。在实际应用中,大多数情况下无线传感器网络获取到的监测信息必须附带相应的位置信息,否则,这些监测信息将失去意义。无线传感器网络研究的一个重要内容就是节点定位技术,它是无线传感器网络的支撑技术,并具有广泛的应用范围[3～4]。研究提高定位精度的技术手段是当前无线传感器网络的热点[5～8]。

按是否需要节点间的距离信息分类,无线传感器网络的定位技术可分为两类:一种是基于测距(rang-based)的技术,另一种是无需测距(rang-free)的技术。在基于测距的定位技术中,角度定位(AOA)和三边定位(Trilateration)是比较常规的定位方法[9]。在三边定位中,极大似然估计、最小二乘法很容易受到测距误差的影响,定位精度较低。随着无线传感器网络定位技术研究的不断深入,许多新的定位算法被不断提出。目前,由于节点硬件资源的不断丰富,处理器性能的不断提高,将粒子群优化算法、遗传算法等智能算法应用于节点定位已经成为一个新的研究方向[10]。粒子群定位算法操作简单、计算量较小,非常适合应用于硬件资源有限的无线传感器网络。文献[11～12]将粒子群优化算法应用于节点定位,通过迭代寻优得到了优于通过极大似然估计、最小二乘法计算得到的节点位置,提高了定位精度。但是,由于粒子群算法的全局寻优能力不足,易陷入局部最优,会造成较大的定位误差。因此,必须对粒子群算法进行改进以提高无线传感器网络定位精度。为了提高粒子群定位算法的定位精度,本文对粒子群算法的速度更新公式以及寻优的目标函数进行改进,以提高粒子群算法的全局寻优能力,且减小测距误差对定位精度的影响。

2粒子群优化算法

粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于集群智能(Swarm-Intelligence,SI)方法的计算技术[12]。该算法由美国学者Eberhart博士和Kennedy博士于1995年提出[13]。

假设在D维的搜索空间内,存在一个种群大小为M的粒子群。每个粒子在空间中的位置坐标xi=(xi1,xi2,…,xid),搜索速度vi=(vi1,vi2,…,vid),搜索到的个体最优位置为pi=(pi1,pi2,…,pid),搜索到的全局最优位置为gb=(gb1,gb2,…,gbd),其中,i=1,2,…,M,d=1,2,…,D。粒子寻优过程中的速度更新公式、位置更新公式及惯性权重计算公式如下

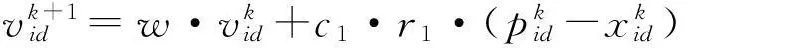
vk+1id= w·vkid+c1·r1·(pkid-xkid)

(1)

(2)

(3)

其中,c1、c2是学习因子,均为非负的常数,常设c1=c2=2;r1和r2是介于[0,1]的随机数;w是惯性权重,用来平衡粒子的全局搜索能力和局部搜索能力,若w较小则有利于提高算法的局部搜索能力,若w较大则有利于提高算法的全局搜索能力;粒子的搜索速度vid∈[-vmax,vmax],vmax太大容易使粒子飞离最优解,vmax太小容易使粒子陷入局部最优,粒子的搜索速度通常设为每维变换范围的10%～20%;k为当前迭代次数;T为终止迭代次数。

3改进的粒子群优化算法

3.1迭代公式的改进

针对粒子群算法后期易陷入局部最优的缺陷,结合无线传感器网络硬件资源受限的实际情况,本文采用一种带有动态扰动项的粒子群优化算法(Particle Swarm Optimization Dynamic Disturbance Term,PSO-DDT)。该算法的速度更新公式变为如下:

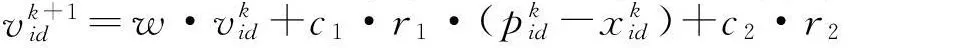
vk+1id= w·vkid+c1·r1·(pkid-xkid)+c2·r2

(4)

rand()是[0,1]之间的随机数;t和h均是[0,1]之间的常数,根据实验情况设定。该算法在粒子速度更新公式中加入动态扰动项,在迭代前期粒子速度较大,动态扰动项对速度的影响可以忽略;随着迭代次数k的增加,粒子速度减慢,扰动项的值增大,保证了粒子在迭代后期速度不为零,且随机数rand()增强了扰动项的扰动性能,可以有效地使粒子跳出局部最优。该算法仅在速度更新式(1)中添加一个动态扰动项,并未增加算法的复杂度,适合无线传感器网络的实际应用。

3.2适应度函数设定

适应度函数即目标函数,用来判断粒子的优劣。粒子在寻优过程中,通过比较适应度函数值的大小来更新个体最优位置和全局最优位置。设100×100m的区域内部署了M个位置已知的节点(锚节点),N个位置未知的节点(盲节点)。锚节点的坐标为Ai(xi,yi)i=1,2,…,M,未知节点的坐标为Nj(xj,yj),j=1,2,…,N,已知锚节点和未知节点的距离测量值di。因为通常情况下,测距误差随着测量距离的增加而增大[14],所以为了减少测距误差对定位精度的影响,本文在适应度函数中引入加权因子。设适应度函数如下:

(5)

(6)

其中,λi为加权因子,0<λi<1;f为一常数,0

3.3算法描述

无线传感器网络的锚节点相当于该算法中的粒子,盲节点的坐标即是粒子要搜索的位置,算法的具体实现流程如下。

1) 初始化粒子种群,种群大小为锚节点数目M。粒子的初始位置为各锚节点的位置,随机设置粒子初速度。计算出各粒子的适应度值,将适应度值最小的粒子的位置设为全局最优位置,将每个粒子的位置设为个体最优位置。

2) 根据式(2)、式(4)更新每个粒子位置和速度。

3) 对于每个粒子,根据式(5)计算更新后的适应度值,若更新后的适应度值小于个体历史最优位置对应的适应度值,则将当前的粒子位置设为个体最优位置;将个体最优位置的适应度值与历史全局最优位置对应的适应度值比较,若个体最优位置的适应度值小于历史全局最优位置的适应度值,则将该粒子位置设为全局最优位置。

4) 检查终止,若达到最大迭代次数kmax,或fitness<ε(ε为距离控制值),则停止迭代;否则转到第2)步。

5) 输出全局最优位置和终止迭代次数。

4实验仿真与分析

4.1仿真参数设定

在Matlab软件上对算法进行仿真实验,独立进行20次实验。各参数设置如下:c1=c2=2;最大迭代次数kmax=500;vmax=5m;惯性权重最大值wmax=0.9,最小值wmin=0.1;t=0.5,h=0.5;f=0.98。距离控制值ε根据平均测距误差设定。设100m×100m的区域内布置四个锚节点和一个盲节点,节点的通信半径为30m。锚节点分别为A1(10,30),A2(20,35),A3(35,15),A4(25,30),盲节点N(x,y)的真实坐标为(5,15),锚节点到盲节点的距离分别为d1,d2,d3,d4。

4.2结果分析

图1分别绘出平均测距误差0%时,初始状态、迭代30次和60次以及迭代终止时粒子位置,粒子最后的位置即是无线传感器网络中盲节点的位置。

图1　节点定位仿真图

设距离控制值ε=2m,在平均测距误差为0%时,PSO算法的终止迭代次数的均值为162次,PSO-DDT算法的终止迭代次数的均值为87次;在平均测距误差为20%时,PSO算法的终止迭代次数的均值为321次,PSO-DDT算法的终止迭代次数的均值为216次。图2绘出不同平均测距误差情况下,最大迭代次数为500次,距离控制值ε=0m,两种算法的适应度函数衰减曲线。由图可知,在平均测距误差为0%和20%两种情况下,当k>50次时适应度函数曲线衰减缓慢,PSO-DDT算法与PSO算法相比,其适应度函数曲线的衰减更快。从仿真的结果可以得出,带有动态扰动项的改进粒子群算法可以克服粒子陷入局部最优,加快收敛速度。

图2　算法的收敛曲线

在平均测距误差不大的情况下,PSO-DDT算法与PSO算法都可以较为准确地计算出未知节点的位置。平均测距误差0%时,PSO算法和PSO-DDT算法计算出的盲节点N的坐标均值分别是(5.0348,15.0120),(5.0234,15.0101)。但随着误差的增大,平均定位误差也逐渐增大,当平均测距误差在25%时,PSO算法的平均定位误差高达27%。由图3可知,PSO-DDT算法与PSO算法相比,其定位精度有所提高,但平均测距误差对两种算法的定位精度影响均较大;在适应度函数中引入加权因子λi后,在一定程度上抑制了坏测距的影响,可以降低平均定位误差。

图3　平均定位误差与平均测距误差的关系

5结语

为了克服粒子群优化定位算法后期易陷入局部最优的缺陷,本文采用一种带有动态扰动项的改进算法进行节点定位。在设计适应度函数时,考虑到测距误差对定位精度的影响,在适应度函数中引入加权因子以削弱测距误差的影响。仿真表明,改进算法能克服粒子早熟,易陷入局部最优的缺点,加快了算法的收敛速度,同时提高了定位精度。但通过仿真实验发现,该算法只能在一定程度上削弱测距误差对定位精度的影响。在实际情况中,各种测距手段均存在不同程度的误差,下一步工作应重点研究减少测距误差的方法。

参 考 文 献

[1] 崔莉,鞠海玲,苗勇.无线传感器网络研究进展[J].计算机研究与发展,2005,42(1):163-174.

CUI Li, JU Hailing, MIAO Yong. Overview of Wireless Sensor Networks[J]. Journal of Computer Research and Development,2005,42(1):163-174.

[2] 刘雨.无线传感器网络中的信息处理[D].北京:北京邮电大学,2006:1-2.

LIU Yu. The information processing in wireless sensor networks[D]. Beijing: Beijing University of Posts and Telecommunications,2006:1-2.

[3] 赵仕俊,唐懿芳.无线传感器网络[M].北京:科学出版社,2013:89-108.

ZHAO Shijun, TANG Yifang. Wireless sensor networks[M]. Beijng: Science Press,2013:89-108.

[4] 李晓维,徐勇军,任丰源.无线传感器网络技术[M].北京:北京理工大学出版社,2007:191-199.

LI Xiaowei, XU Yongjun, REN Fengyuan. Techniques for wireless sensor networks[M]. Beijing: Beijing Institute of Technology Press,2007:191-199.

[5] Li F F, Luo F, Wang J X, et al. An effective self-adapting localization algorithm in wireless sensor networks[J]. Journal of Applied Mechanics and Materials,2011,58-60:1013-1017.

[6] Jian L R, Zheng Y, Liu Y H. Beyond triangle inequality: Sifting noisy and outlier distance measurements forlocalization[C]//Proc of IEEE INFOCOM 2010. San Diego: IEEE Press,2010:1-9.

[7] Kung H T, Lin C K, Lin T H, et al. Localization with snap-inducing shaped residuals: Coping with errors in measurement[C]//Proc of MobiCom 2009. Beijing: ACM Press,2009:333-344.

[8] Li Z, Trappe W, Zhang Y, et al. Robust statistical methods for securing wireless localization in sensor networks[C]//Proc of IPSN 2005. Los Angeles: IEEE Press,2005:91-98.

[9] NICULESC D, NATH B. Ad Hoc Positioning Systems(APS) Using AOA[J]. In: Proc. of the IEEE INFOCOM 2003,2003(3):1734-1743.

[10] 彭宇,王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报,2011,25(5):389-399.

PENG Yu, WANG Dan. A review: wirless sensor networks localization[J]. Journal of Electronic Measurement and Instrument,2011,25(5):389-399.

[11] 王晓乐,徐家品.基于粒子群优化算法的WSNs节点定位研究[J].计算机应用,2009,29(2):494-499.

WANG Xiaole, XU Jiapin. Research on node localization based on particle swarm optimization for WSNs[J]. Journal of Computer Applications,2009,29(2):494-499.

[12] 陈志奎,司威.传感器网络的粒子群优化定位算法[J].通信技术,2011,44(1):102-104.

CHEN Zhikui, SI Wei. Particle Swarm Optimization Localization Algorithm for Wireless Sensor Networks[J]. Communications Technology,2011,44(1):102-144.

[13] 高玮,尹志喜.现代智能仿生算法及其应用[M].北京:科学出版社,2011:178-190.

GAO Wei, YIN Zhixi. Modern bionic algorithm and its application[M]. Beijing: Science Press,2011:178-190.

[14] Wang Xi-huai, Li Jun-jun. Hybrid particle swarm optimization with simulated annealing[C]//Proc of Int Conf on Machine Learning and Cybernetics. Shanghai: IEEE,2004:2402-2405.

[15] Chen W, Mei T, Sun L, et al. Error analyzing for RSSI-based localization in wireless sensor networks[C]//Intelligent Control and Automation, 2008. WCICA 2008. 7th World Congress on. IEEE,2008:2701-2706.

An Improved Localization Method Based on Modified Particle Swarm Optimization for Wireless Sensor Networks

ZHANG XianchaoLIU Xingchang

(Department of Logistics Information & Logistics Engineering, Logistics Engineering University, Chongqing401311)

AbstractLocating nodes accurately is an important branch of wireless sensor networks researching. Algorithm of locating wireless sensor networks based on particle swarm optimization is more accurate comparing with those based on maximum likelihood estimation or/and least squares estimation, but locally optimal. Aiming to correct the defects mentioned above, a modified algorithm with a dynamic disturbance term is introduced to locate wireless sensor networks, also, weighting factors are led into the objective function to weaken the effect from range error. In light of the evidence, this algorithm could quicken convergence rate and improve position precision.

Key Wordswireless sensor networks, particle swarm optimization, dynamic disturbance term, position precision

* 收稿日期:2015年11月3日,修回日期:2015年12月26日

作者简介:张先超,男,硕士研究生,研究方向:无线传感器网络节点定位技术。刘兴长,男,博士,教授,硕士生导师,研究方向:无线传感器网络。

中图分类号TP393

DOI:10.3969/j.issn.1672-9722.2016.05.016