基于能量谱和双谱的跳频信号融合检测方法*

王建雄　张立民　钟兆根

(1.海军航空工程学院电子信息工程系　烟台　264001)(2.海军航空工程学院融合所　烟台　264001)



基于能量谱和双谱的跳频信号融合检测方法*

王建雄1张立民2钟兆根1

(1.海军航空工程学院电子信息工程系烟台264001)(2.海军航空工程学院融合所烟台264001)

摘要针对跳频信号能量检测法中遇到的问题,论文设计推导了一种基于能量谱和双谱的融合检测算法。该方法通过融合能量谱法得到观测信号的二阶统计信息和双谱法得到的三阶统计信息,分析可利用的检测信息,从而完成对跳频信号的盲检测。仿真结果表明,不管是在高斯信道还是瑞利衰落信道等环境下,该文算法相比能量检测法和双谱法都具有更好的性能。并且数据越长的信号,其检测性能越好。

关键词跳频信号; 能量检测; 双谱检测; 通信侦察

Class NumberTN911

1引言

在现代电子对抗中,信号环境十分恶劣,不但信号分布密集,而且种类繁多,各种信号混杂在一起,电磁环境十分复杂,这样针对跳频信号的检测就变得更加困难。跳频侦察设备要想侦察到敌方的跳频信号,只有等敌方电台进行通信时才需要开始工作,在无敌方电台信号时,侦察设备也无需进行跳频信号的分析处理,但是敌方电台何时开始工作是事先未知的,这就涉及到跳频信号的盲检测问题,只有先检测到有跳频信号的存在,才能开始做信号的分选和估计工作。

目前对跳频信号的检测提出了一些方法,主要有小波变换检测法[1～2]、循环谱检测法[3～5]、自相关检测法[6～7]、自适应多信道检测技术[8]、压缩接收机检测技术[9]、数字信道化技术[10]、压缩信道化检测技术[11]、最大相关处理法和复杂电磁环境下的检测技术[34]等。然而这些检测方法大都是在白噪声的条件下进行的,而且需要信号的部分先验知识,然而实际短波超短波频段密集分布着各种干扰信号,而且信号能量也不稳定,这使得已有的检测方法得不到较好的效果,有的方法还需已知信号的一些先验知识。因此,对于无任何先验知识的超短波跳频信号检测问题有必要进一步展开深入的研究。

本文介绍了一种基于能量谱和双谱的融合跳频信号盲检测方法,在建立信号模型的基础上,分析了能量检测法中存在的问题,并充分利用跳频信号及噪声的非高斯特性,设计推导了一种基于能量谱和双谱的融合检测算法。

2信号模型

根据信号环境的实际特性,可将链路侦察模型建为

x(t)=s(t)*h(t)+n(t)

(1)

式中I(I≥0)为信号个数,si(t)为第i个网台跳频信号,h(t)是未知的信道冲激响应,n1(t)为加性高斯噪声,n2(t)为加性非高斯噪声。

为简化下面的推导,令式(1)的h(t)=1,即瞬态混合模型。若H0表示“仅有噪声”,H1表示“存在信号”,则能量谱检测可表述为

(2)

式中T1为根据n(k)设置的检测门限。从式(2)和文献[16]的分析可知能量谱检测与SNR是密切相关的:当SNR较大时,检测性能具有很强的鲁棒性,且与噪声的具体形式无关;当SNR较小时,噪声能量Pn和信号能量Ps将相差不大,导致检测性能随着SNR的降低而急剧下降。

若采用双谱检测,则可表述为

(3)

式中T2为根据n2(k)设置的检测门限。从式(3)可知:双谱检测的性能仅与n2(k)和s(k)的双谱信息有关,即使在SNR很小的情况下,只要信号的双谱值Bs足够大,就有望获得较高的检测概率。由此可见,基于能量谱和双谱的融合检测同时利用了观测信号的二阶和三阶统计信息,增加了可利用的检测信息,有利于检测性能的提高。

3算法原理推导

针对跳频信号的检测,下面分别讨论能量谱检测和双谱检测的实现步骤,并针对两者的优缺点,设计一种用于跳频信号的融合检测方法。

1) 能量谱检测

本文采用平均周期图法计算接收信号的能量谱,其表达式为

(4)

(5)

式中a(i)为数据窗,本文选用矩形窗,xk为第k-段接收信号。

若观测噪声n(k)服从高斯分布,则用平均周期图法得到的噪声能量谱也满足高斯分布。设定Pfa查正态分布表得gT,进而求出绝对门限T1=μ+gT·σ(均值μ和标准差σ可用直方图等方法估计)。若Px(ω)>T1,就认为在Pfa下检测到信号,即否定H0,检测结果为H1。

2) 双谱检测

双谱是信号三阶相关的Fourier变换,对高斯信号不敏感,具有很好的抗高斯噪声的能力。很多数字调制的通信信号都是非高斯信号(准确说是亚高斯信号),目前仅有频分复用(OFDM)信号满足高斯特性。所以双谱可用来定量地描述这些信号的非高斯特性[13]。

假设接收信号的双谱为B(ωi,ωk),在数据长度较短时,估计方差会很大。用直接法估计N点接收信号的双谱为Bx(ωi,ωk),为减少双谱估计误差,采用时域和频域双重平滑:频域平滑窗宽为L,时域采用K段平均。并根据文献[14]推导出的双谱最优窗,用直接法来估计双谱,通过参数“wind”来指定最优窗的窗口长度,在一般情况下,窗口长度越大,平滑效果越好,本文采用默认值5。另外一种方法是通过适当增加数据分段数目,使数据点部分重叠,从而降低估计方差。

为解决双谱检测的巨大运算量,结合对角切片能反映双谱主要特征信息的特点,取双谱对角切片上的K个点,则Bx(ωi,ωk)可表述为

(6)

(7)

式中2L1+1=L,N0·L=W,Δ0=fs/N0。当L=1时,式(6)可化简为

(8)

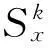
下面讨论检测统计量的确定,对于较大的N(N>256),文中选取文献[15]提出的检测量确定方法:

(9)

式中Px(w)可通过式(5)求得。

可以证明,β近似服从复高斯分布Nc(0,1)。当H0成立时,可进一步证明:

(10)

服从复高斯分布Nn(Bn2(ωi,ωk),1),于是修改该检测量为

(11)

式中m为主值域中选取的离散双谱点数。

从式(11)可知TCH需预先知道纯噪声背景的双谱估计和功率谱估计,在通常情况下这一点是难以满足的,则进一步修改检测量为

(12)

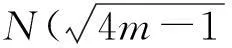
能量谱检测在SNR较大时有较强的鲁棒性,而与噪声的具体形式无关;但是当SNR较小时,噪声能量谱和信号能量谱相差不大,导致正确检测概率随SNR的降低急剧下降。双谱检测的检测性能仅与非高斯噪声和信号的双谱信息有关,即使在SNR很小的情况下,只要作为揭示信号非高斯性的双谱值足够大,也有望获得较高的检测概率。鉴于上述方法的互补性,本文设计了图1所示的融合检测算法。

图1　融合检测算法的原理结构图

图1中“检测结果融合”的逻辑为

1) 当SNR较大时,若无非高斯噪声或非高斯噪声的双谱值相对信号的双谱值很小,两种方法均能检测到信号,则判决为有信号;

2) 当SNR较大时,能量谱法能检测到信号,若非高斯噪声的双谱值相对信号的双谱值较大而使双谱检测法不能检测到信号,则判决为有信号;

3) 当SNR较小时,若能量谱法未能检测到信号,同时无非高斯噪声或非高斯噪声的双谱值相对信号的双谱值很小使双谱检测法能检测到信号,则判决为有信号;

4) 当SNR较小时,若能量谱法未能检测到信号,同时非高斯噪声的双谱值相对信号的双谱值较大而使双谱检测法未能检测到信号,则判决为无信号。

根据上述逻辑,则在Pfa下本文算法的盲检测概率为

(13)

4仿真分析

在进行对融合检测仿真时,选取3000个样本点作为实验样本,采样频率为30kHz,跳频信号的跳频速率为100hop/s。采用均方根升余弦成形滤波,α=0.5,高斯白噪声信道和Rayleigh衰落信道,数据长度2048,分段计算FFT的长度2048,SNR从-15dB变化到-3dB,Pfa=10-2,图2是运用能量谱法、双谱法及本文算法的检测性能对比曲线。当选择的数据长度分别为2048、10240、20480时,数据长度对算法检测性能的影响曲线如图3所示。

由图2可知:不管是在AWGN信道还是Rayleigh衰落信道等环境下,本文算法性能均优于能量谱法和双谱法,具有更好的环境适应能力。由图3可知:数据越长,检测性能越好,这是因为它是基于能量谱和双谱的融合检测,而数据长度对这两种方法本来就存在这样的影响。

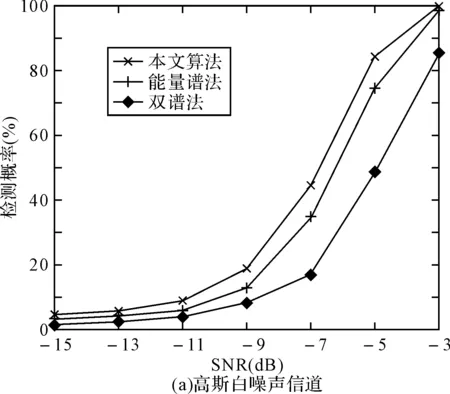
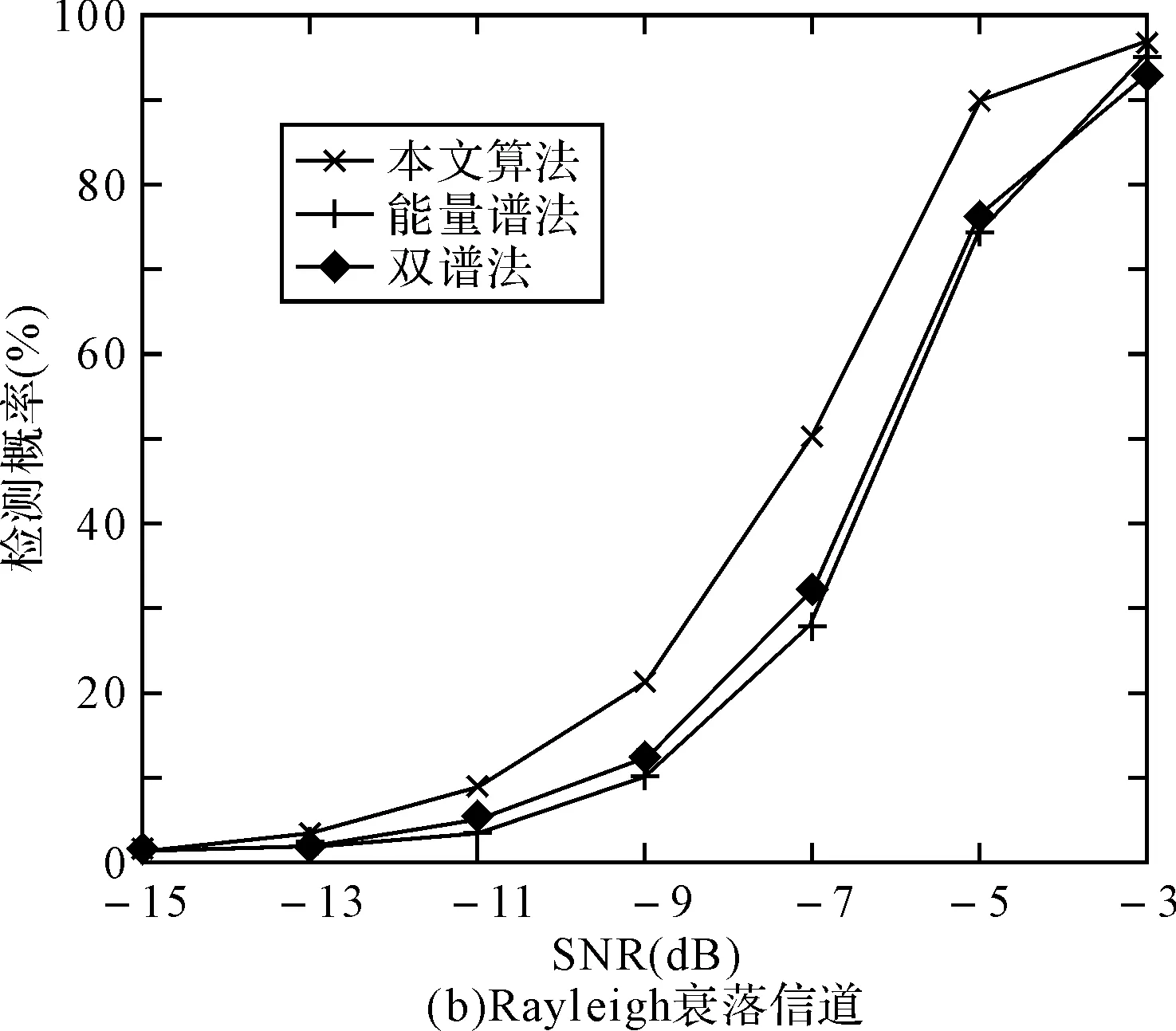
图2　不同信道环境下各种算法的检测性能对比

图3　数据长度对检测性能的影响

5结语

针对能量检测法对信噪比敏感,并且检测性能不好的问题,充分利用跳频信号及噪声的非高斯特性,设计推导了一种基于能量谱和双谱的融合检测算法。本文分别采用能量检测法、双谱法和融合检测法三种方法在不同信噪比条件下对跳频信号跳频信号进行了检测仿真实验,检测结果表明,较于能量谱和双谱的融合检测方法,不管是在AWGN信道还是Rayleigh衰落信道等环境下,本文算法性能均具有更好的环境适应能力。并且数据越长的信号,其检测性能越好。

参 考 文 献

[1] Xiaojing Wu, Weiming Guo, Wensheng Cai, et al. A method based on stochastic resonance for the detection of weak analytical signal[J]. Talanta,2003,61(6):863-869.

[2] Monique P. Fargues, Howard F. Overdyk, Ralph Hippenstiel. Wavelet-based Detection of Frequency Hopping Signals[C]//STL. Proceeding of SSCC’97. New York: Institute of Electrical and Electronics Engineers,1997:515-519.

[3] Reed D E, Wickert M A. Minimization of detection of symbol-rate spectral lines by delay and multiply receivers[J]. IEEE Transactions on Communications,1988,36(1):118-120.

[4] Reed D E, Wickert M A. A performance comparison of optimum and sub-optimum receiver structures for rate-line detection of digitally modulated carriers[C]//Proceeding of IEEE Region 5 Conference on Spanning the Peaks of Electrotechnology, Colorado Springs, CO, USA, March,1988:177-181.

[5] Kuehls J F, Geraniotis E. Presence detection of binary-phase-shift-keyed and direct-sequence spread-spectrum signals using a prefilter-delay-and-multiply device[J]. IEEE Journal on SAIC,1990,8(5):915-933.

[6] A. Polydoros, K. f. Woo. LPI Detection of Frequency Hopping Signal Using Autocorrelation Techniques[J]. IEEE Selected Areas in Communications,1985,SAC(3):714-726.

[7] S. Hinedi, A. Polydoros. DS/LPI Autocorrelation Detection in Niose Plus Random-Tone Interference[J]. IEEE Transaction on Communications,1990,38(6):805-817.

[8] 罗来源.扩频低截获率信号的检测技术[J].电信技术研究,1997,10:10-15.

LUO Laiyuan. Detection Technology of Spread Spectrum Low Intercept Rate Signal[J]. Research on Telecommunication Technology,1997,10:10-15.

[9] 王军.数字信道化技术在跳频信号侦察中的应用[J].电信技术研究,2000,1:32-34.

WANG Jun. Digital Channelized Technology in The Application of The Frequency Hopping Signal Reconnaissance[J]. Research on Telecommunication Technology,2000,1:32-34.

[10] 冯富强,刘德树.一种对跳频信号的截获和分类识别的新方法[J].中国人民解放军电子工程学院学报,1995,4:65-68.

FENG Fuqiang, LIU Deshu. A New Method on Interception, Classification and recognition of Hopping Signal[J]. Journal of Electronic Engineering institute of PLA,1995,4:65-68.

[11] 徐启华.最大相关处理在超短波跳频信号侦察中的应用[J].电信技术研究,2000,1:25-27.

XU Qihua. Most Correlation Process in The Application of Ultrashort Wave Frequency Hopping Signal Reconnaissance[J]. Research on Telecommunication Technology,2000,1:25-27.

[12] 杨宏娃.复杂电磁环境下跳频信号的检测技术[C]//中国电子学会电子对抗分会第十二届学术年会论文集,2005:475-479.

YANG Hongwa. Detection Technology of Hopping Signal in Complex Electromagnetic Environment[C]//The Twelfth Academic annual Conference Proceeding about Electronic Countermeasures branch of CIE,2005:475-479.

[13] 张贤达.现代信号处理[M].第二版.北京:清华大学出版社,2002:97-100.

ZHANG Xianda. Modern Signal Processing[M]. Tsinghua University Press,2002:97-100.

[14] Olcay Akay, Erten Erözden. Employing fractional autocorrelation for fast detection and sweep rate estimation of pulse compression radar waveforms[J]. Signal Processing,2009,89(12):2479-2489.

[15] Kai M H. Narrowband weak signal detection by higher order spectrum[J]. IEEE Transactions on Signal Processing,1996,44(4):874-879.

[16] Lehtomäki J, Juntti M, Saarnisaari H. CFAR strategies for channelized radiometer[J]. IEEE Signal Processing Letters,2005,12(1):13-16.

Fusion Detection Algorithm of FH Signal Based on Energy Spectrum and Bispectrum

WANG Jianxiong1ZHANG Limin2ZHONG Zhaogen1

(1. Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai264001)(2. Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai264001)

AbstractTo deal with the problem in energy detection algorithm of FH signal, a fusion detection algorithm is introduced based on energy spectrum and bispectrum. Based on analyzing the second-order statics through energy spectrum and third-order statics through bispectrum, the algorithm realizes the detection of FH signal. Simulation results indicate that the algorithm has a better performance than energy detection algorithm and bispectrum detection algorithm in Gauss channel or Rayleigh channel and that the detection performance is better, when the data is longer.

Key Wordsfrequency hopping, energy detection, bispectrum detection, communication reconnaissance

* 收稿日期:2015年11月13日,修回日期:2015年12月23日

基金项目:国家自然科学基金(编号:60972159,61102167);航空科学基金(编号:20085184003);泰山学者工程专项经费(编号:ts201511020)资助。

作者简介:王建雄,男,博士研究生,研究方向:盲信号处理。张立民,男,博士,教授,研究方向:通信信号处理。钟兆根,男,博士,讲师,研究方向:盲信号处理。

中图分类号TN911

DOI:10.3969/j.issn.1672-9722.2016.05.019