基于虚拟导纳的大型光伏电站谐波抑制策略研究

杨立滨，张海宁，李春来，杨 军，郑 晨，王 平

(1.国网青海省电力公司电力科学研究院，青海 西宁 810008；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044)

基于虚拟导纳的大型光伏电站谐波抑制策略研究

杨立滨1，张海宁1，李春来1，杨 军1，郑 晨2，王 平2

(1.国网青海省电力公司电力科学研究院，青海 西宁 810008；2.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044)

在建立大型光伏电站诺顿等效模型基础上通过阻抗分析法分析了大型光伏电站与电网之间以及光伏电站内逆变器之间的耦合作用，揭示了大型光伏电站谐波产生机理，即电网阻抗与逆变器等效输出导纳相互作用对某一频率处的谐波产生了放大作用。提出在逆变器输出端增加一条虚拟的导纳通路来消除系统对谐波的放大作用。将并网点电压通过由一阶惯性环节和二阶陷波器复合而成的系统反馈至控制器输出端，实现对逆变器等效输出导纳的改善。经该方法改善后的系统输出导纳对谐波具有滤除作用，且对基波无衰减。仿真及实验验证了理论分析的正确性。

大型光伏电站；电网阻抗；虚拟导纳；谐波治理

0 引言

随着能源危机的加剧和环境问题的突出，近年来以大型光伏电站为代表的光伏产业得到迅猛发展[1-5]。大电网的非理想特性使得电网阻抗与光伏电站等效输出阻抗之间产生交互影响，导致并网点电压和电流的谐波含量增大，当谐波超过一定量时，光伏电站就会与系统解列[4-5]。因此有必要对大型光伏电站并网谐波抑制策略进行研究。

目前已有相关文献提出了针对大型光伏电站谐波治理的方法，文献[6]提出一种电能质量复合控制策略，该策略能够使光伏电站同时具有无功补偿和谐波抑制的功能，但该方法无法解决由于电网阻抗变化导致的谐波问题；文献[7]在系统并网公共连接点处添加一台阻性有源阻尼器，对解决系统的谐波有一定的效果，但该方法需要另外添加硬件装置，提高了系统成本，降低了可靠性。也有部分文献提出了针对单台逆变器并网谐波问题的解决方案，文献[8-9]通过检测谐波频率、电网阻抗等，在线调整控制器参数，但该类方法需要复杂的检测与控制算法；文献[10]采用无差拍控制对系统谐波进行抑制，但该方法需要采用状态观察及对收敛性进行设计，控制器设计复杂，且通用性较差。因此，难以将上述针对单台逆变器谐波问题的解决方法借鉴到大型光伏电站中。

基于上述分析，本文首先建立大型光伏电站诺顿等效模型，对大型光伏电站与电网之间的交互作用进行分析，揭示出大型光伏电站谐波产生机理，然后根据该机理提出在逆变器输出端添加一个能够通过谐波阻基波的导纳来实现对谐波的抑制，并给出了一种实现方案。最后通过仿真和实验验证了本文所提谐波抑制策略的有效性。

1 大型光伏电站谐波产生机理

1.1 大型光伏电站建模

大型光伏电站通常由多台带 LCL 滤波器的并网逆变器组成，其等效电路结构如图1 所示。其中分别为逆变器 j的逆变器侧电感、滤波电容及网侧电感，为第 j 台逆变器的三相并网电流，分别为逆变器 j的逆变桥输出三相电压、电流，为并网点三相电压，为等效电网阻抗，主要包含中低压输电线路和升压变压器的感性分量和阻性分量，系统的谐波主要由感性分量引起，因此本文只考虑感性分量，记对应的导纳

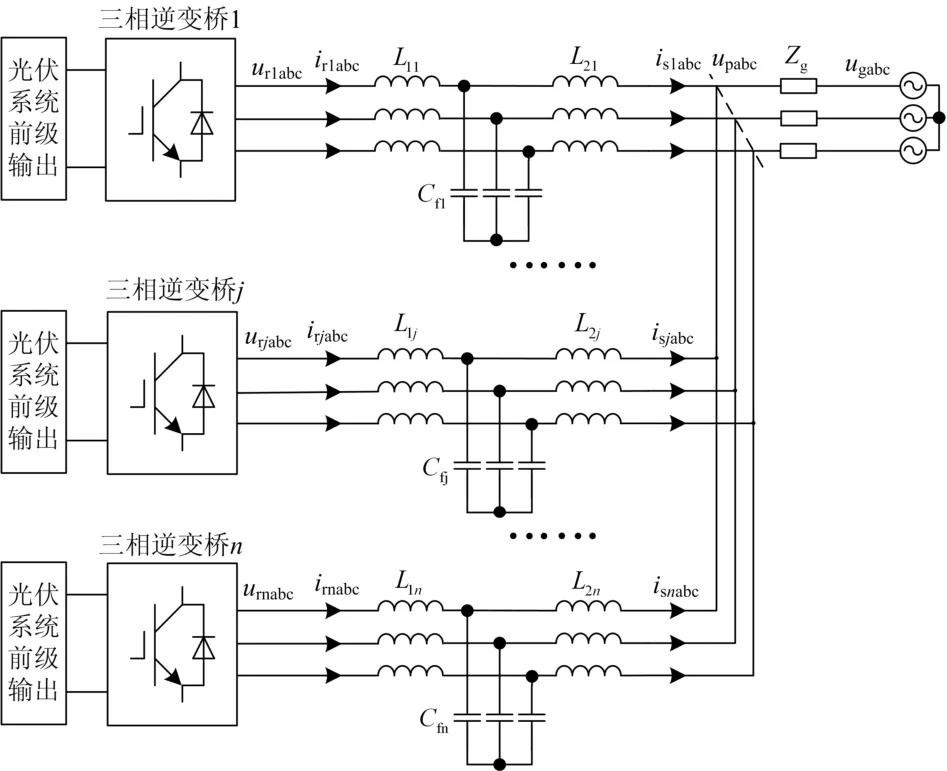
图1 大型光伏电站拓扑结构Fig. 1 Topology of LSPV plants

对于大型光伏系统，为了提高效率，尽量降低在电能变换过程中的能量损耗，其控制结构多选为单级式结构。逆变器 j 在两相静止坐标系下的控制结构如图2 所示，为电容电流有源阻尼系数。并网参考电流由MPPT产生的功率参考值和并网点电压经瞬时功率理论合成，以实现功率控制。

图2 两相静止坐标系下并网逆变器控制策略Fig. 2 Control strategy of the grid-connected inverter in two-phase stationary coordinate system

准 PR 控制器在基波频率处具有很高的增益，对正弦交流量能够实现无静差控制，采用准 PR控制器对并网电流进行控制，其数学模型如式(1)所示。由于在两相静止坐标系下 α、β轴是对称的，因此仅以α轴为例进行分析，系统在s域下的控制结构如图3所示。

图3 系统复频域数学模型Fig. 3 System model in complex frequency domain

根据叠加原理，在图3中分别让参考电流和并网点电压单独作用可以得到大型光伏电站α轴下的诺顿等效模型，如图4所示。图中：

在经济上，要想实现可持续发展，要尊重自然、爱护自然，确保经济活动的合理性。通过加强环保工程运行的管理和控制，必须要积极推进工程项目，严格监管整个环保工程的实施过程，确保良好的工程成效。

图4 a轴下大型光伏电站诺顿等效模型Fig. 4 LSPV equivalent Norton model in α axis

1.2 大型光伏电站谐波产生机理

根据图4中的大型光伏电站诺顿等效模型可以得到电站中逆变器 j的并网电流如式(2)所示。

工程实际中大型光伏电站的所有逆变器通常采用相同的电路结构和参数可以认为每台逆变器的闭环传递函数、等效输出导纳相同，记为：，因此根据大型光伏电站的诺顿等效模型，可以将每台逆变器的并网电流转化为

通常情况下逆变器自身对谐波电流具有衰减作用，且电网阻抗对谐波也具有衰减作用，因此逆变器并网电流中所含谐波量主要取决于：

当电网阻抗不存在时，每台逆变器的输出电流与自身参数以及电网电压有关，各逆变器之间不存在相互作用。以 3 MW 大型光伏电站为例，系统参数如表1 所示，系统时域仿真波形如图5(a)所示，可以看出并网电流及并网点电压良好，满足并网要求。但实际电网中均存在一定的阻抗，且该阻抗随电网运行方式的变化而变化，使得电站中各逆变器之间会存在相互耦合，且电网对每台逆变器并网电流的影响更加复杂。当|Gx(jω)|在某一频率处大于 1时，该频率处的电流将被放大，系统中将会出现大量该频率处的谐波。

表1 系统参数Table 1 System parameters

图5 原始系统时域仿真波形Fig. 5 Simulated waveforms of original system in time domain

图6 原始系统的伯德图Fig. 6 Bode diagram offor original system

2 基于虚拟导纳的谐波抑制策略

由前面的分析可知，大型光伏电站的谐波是由于逆变器输出阻抗与等效电网阻抗相互作用的结果，可以采用改变电网阻抗参数或者逆变器输出阻抗的方法来避免系统对谐波的放大作用，进而达到抑制系统谐波的目的。

改变电网阻抗参数可以通过安装可控串联补偿器(TCSC)或者其他无源元件来实现，但这种方法增加了成本、降低了可靠性，不利于系统的经济运行。另外由于电网阻抗是实时变化的，改变电网阻抗的方法并不能从根本上消除系统谐波。

抑制系统谐波更有效的方法是通过一定的控制算法，实现对逆变器输出阻抗的改善，使得式(4)对谐波具有衰减作用，进而达到抑制谐波电流的目的。本文提出在逆变器输出端增加一条谐波通路的方法来对谐波进行抑制。在每台逆变器输出端增加一条谐波通路后大型光伏电站诺顿等效模型如图7所示。为了抑制谐波，所添加的谐波通路导纳应满足以下特性：

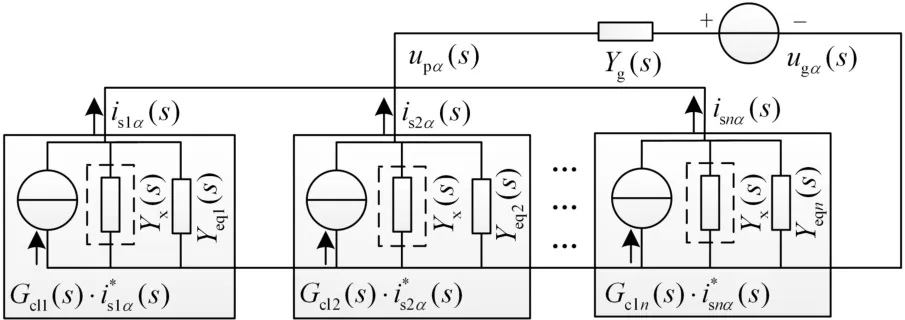
图7 增加虚拟导纳后的诺顿等效模型Fig. 7 LSPV equivalent Norton model in α axis with virtual admittance

根据以上特性本文选择式(5)作为在逆变器输出端所添加的虚拟导纳，该式等号右边前两项主要用来调节幅值，使得在基波频率处的幅值很小，而在其他频率处的幅值很大，达到滤除谐波的目的；等号右边第三项主要用来调节相位，以使相位裕度满足要求。

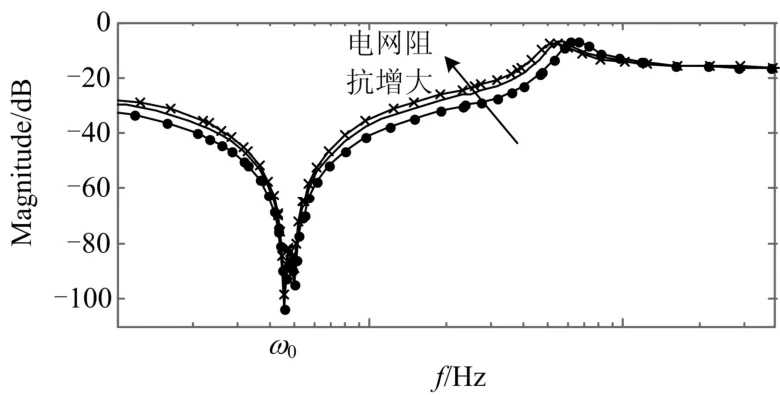
图8 增加虚拟导纳后系统的伯德图Fig. 8 Bode diagram offor original system after adding virtual admittance

采用并网点电压反馈的方式来实现在逆变器输出端增加一个虚拟导纳，其控制结构如图9所示。

图9 虚拟导纳实现的控制结构框图Fig. 9 Structure diagram of realizing virtual admittance

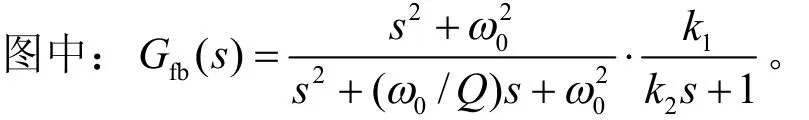
可以看出，本文所提出的谐波抑制策略只需要在逆变器中增加一个并网点电压前馈环节即可，工程中易于实现。

3 仿真分析

为了验证本文理论分析的正确性，根据图1、图2 所示的原理图在 Matlab 中搭建额定功率为 3 MW的大型光伏电站仿真模型，逆变器参数如表1所示。电网采用三相交流理想电压源模拟，电网阻抗采用集中参数电感模拟，光伏电池采用文献[12]中的数学模型搭建。

可以看出两种电网阻抗情况下，在逆变器输出端添加一个虚拟导纳后，系统中的谐波均得到了很好的抑制，并网电流和并网点电压波形恢复良好，谐波含量降低，满足并网要求。

图10 时的仿真结果Fig. 10 Simulation results with

图11 时的仿真结果Fig. 11 Simulation results with

4 实验分析

为进一步验证本文所提谐波抑制策略的有效性，并考虑到实验条件的限制，仅以两台完全相同的逆变器为例进行实验分析。每台逆变器输入功率为 5 kW，控制策略采用 TMS320F28335 控制器实现，实验主要参数如表2所示。由于两台逆变器完全相同，因此仅以其中一台逆变器的实验结果为例进行分析。

表2 实验系统电路参数Table 2 Circuit parameters of experiment system

(1) 两台逆变器均不采用谐波抑制策略，当电网阻抗分别取 1 mH、2 mH 时分别运行两台逆变器，1#逆变器的并网电流波形如图12 所示。

由图12 可以看出，在不添加任何谐波抑制策略的情况下，随着电网阻抗的增加，系统谐波含量增加，并网电流及并网点电压波形均变差，不满足并网要求。

(2) 两台逆变器均加入本文所提谐波抑制策略，当电网阻抗分别取 1 mH、2 mH 时分别运行两台逆变器，1#逆变器的并网电流波形如图13 所示。

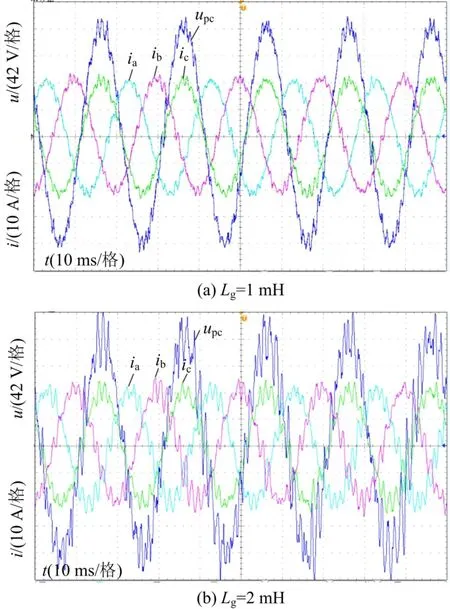
图12 无抑制策略时实验结果Fig. 12 Experimental results without harmonic suppression strategy

图13 添加虚拟导纳后实验结果Fig. 13 Experimental results with virtual admittance

对比图12 和图13 可以看出，在采用本文所提谐波抑制策略后，随着电网阻抗的增加，系统并网电流波形始终良好，谐波含量较小，满足并网要求。

5 结论

本文针对大型光伏电站与电网之间的交互作用，首先根据工程实际中常用的大型光伏电站拓扑结构建立了诺顿等效模型；然后对光伏电站与电网之间的相互影响进行分析，并揭示出光伏电站产生谐波的机理；最后根据该机理提出在逆变器输出端添加一个虚拟导纳的方法来抑制谐波，通过一定的设计方法使得该虚拟导纳在谐波频率处的值很大，在基波频率处的值很小，因此具有通谐波阻基波的特性，实现了对光伏电站中谐波的抑制。该方法只需要在逆变器中增加一个并网点，电压前馈环节即可，工程中易于实现。

[1]孔令国, 蔡国伟. 大规模并网光伏电站的逆变器控制方 法 研 究 [J]. 电 力 系 统 保 护 与 控 制 , 2013, 41(22): 57-63. KONG Lingguo, CAI Guowei. Research on control method of inverters for large-scale grid-connected photovoltaic power system[J]. Power System Protection and Control, 2013, 41 (22): 57-63.

[2]周林, 曾意, 郭珂, 等. 具有电能质量调节功能的光伏并网系统研究进展 [J]. 电力系统保护 与控制, 2012, 40(9): 137-145. ZHOU Lin, ZENG Yi, GUO Ke, et al. Development of photovoltaic grid-connected system with power quality regulatory function[J]. Power System Protection and Control, 2012, 40(9): 137-145.

[3]RUBÉN I, TAKESHI S, YOSUKE F, et al. Parallel connection of grid-connected LCL inverters for MW-scaled photovoltaic systems[C]// International Power Electronics Conference. Sapporo, Japan, 2010: 1988-1993.

[4]杨明, 周林, 张东霞, 等. 考虑电网阻抗影响的大型光伏电站并网稳定性分析[J]. 电工技术学报, 2013, 28(9): 214-223. YANG Ming, ZHOU Lin, ZHANG Dongxia, et al. Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 214-223.

[5]周林, 张密, 居秀丽, 等. 电网阻抗对大型并网光伏系统 稳 定 性 影 响 分 析 [J]. 中 国 电 机 工 程 学 报 , 2013, 33(34): 34-41. ZHOU Lin, ZHANG Mi, JU Xiuli, et al. Stability analysis of large-scale photovoltaic plants due to grid impedances[J]. Proceedings of the CSEE, 2013, 33(34): 34-41.

[6]黄冬冬, 吴在军, 窦晓波, 等. 光伏规模化并网的电能质量复合控制策略研究[J]. 电力系统保护与控制, 2015, 43(3): 107-112. HUANG Dongdong, WU Zaijun, DOU Xiaobo, et al. A power quality composite control strategy based on largescale grid-connected photovoltaic power generation[J]. Power System Protection and Control, 2015, 43(3): 107-112.

[7]WANG X, BLAABJERG F, LISERRE M, et al. An active damper for stabilizing power electronics based AC systems[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3318-3329.

[8]PÊNA-ALZOLA R, LISERRE M, BLAABJERG F, et al. A self-commissioning notch filter for active damping in a three-phase LCL-filter-based grid-tie converter[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6754-6761.

[9]CESPEDES M, SUN J. Adaptive control of gridconnected inverters based on online grid impedance measurements[J]. IEEE Transactions on SustainableEnergy, 2014, 5(2): 516-523.

[10]MOHAMED Y. Suppression of low- and high-frequency instabilities and grid-induced disturbances in distributed generation inverters[J]. IEEE Transactions on Power Electronics, 2011, 16(12): 3790-3803.

[12]胡文翠, 王明渝, 钱坤. LCL 型并网逆变器电流控制器设计[J]. 电力系统保护与控制, 2013, 41(8): 124-128. HU Wencui, WANG Mingyu, QIAN Kun. Design of current controller for grid-connected inverter with LCL filter[J]. Power System Protection and Control, 2013, 41(8): 124-128.

[13]王以笑, 张新昌, 路进升, 等. 基于 DIgSILENT 的并网光伏发电系统的建模与仿真[J]. 电力系统保护与控制, 2014, 42(3): 49-55. WANG Yixiao, ZHANG Xinchang, LU Jinsheng, et al. Modeling and simulation of grid-connected PV system based on DIgSILEN software[J]. Power System Protection and Control, 2014, 42(3): 49-55.

Harmonic suppression strategy of large-scale photovoltaic plants based on virtual admittance

YANG Libin1, ZHANG Haining1, LI Chunlai1, YANG Jun1, ZHENG Chen2, WANG Ping2
(1. Electric Power Research Institute of State Grid Qinghai Electric Power Company, Xining 810008, China; 2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, China)

Based on the equivalent Norton model of large-scale photovoltaic (LSPV) plants, the coupling among inverters in LSPV plant and between LSPV plant and the grid are studied through impedance analysis. The study reveals the harmonic mechanism that coupling between grid impedance and equivalent admittance of inverter will amplify harmonics in the system. To remove the amplification to harmonics, the strategy of adding a virtual admittance to filter harmonics is proposed. The strategy is realized to improve inverter admittance by the voltage at the point of common coupling (PCC) feedback through the combination of a first-order process and a second-order notch filter. The system with the proposed strategy owns characteristics of making harmonic current through the virtual admittance and fundamental frequency current blocked. In the end, the result of simulation and experiment validates theoretical analysis.

LSPV plants; grid impedance; virtual admittance; harmonic suppression

10.7667/PSPC151696

：2015-11-24

杨立滨(1985-)，男，硕士，高级工程师，从事风电、太阳能等新能源发电及并网技术领域的研究工作；

(编辑 姜新丽)

青海省光伏发电并网技术重点实验室(2014-Z-Y34A)

郑 晨(1990-)，男，通信作者，博士研究生，主要从事电网阻抗对光伏系统稳定性影响方面的研究 。E-mail: zhengchen725@163.com