基于协同演化博弈算法的微网和配电网动态优化

徐意婷，艾 芊，胡剑生

(1.上海交通大学电子信息与电气工程学院，上海 200240；2.许继集团有限公司，河南 许昌 461000)

基于协同演化博弈算法的微网和配电网动态优化

徐意婷1，艾 芊1，胡剑生2

(1.上海交通大学电子信息与电气工程学院，上海 200240；2.许继集团有限公司，河南 许昌 461000)

微网和配电网在互动运行时是相互影响、相互制约的。为了使整个系统获得最好的效益，需要整合考虑微网和配电网的效益。微网和配电网作为两个需要同时优化的主体，具有一定的效益冲突。研究微网和配电网互动运行时相互影响情况，分别分析其运行效益，将效益目标作为虚拟博弈参与者建立了模型，并采用模糊数学方法将其隶属化。结合演化博弈理论和协同进化算法，提出了一种协同演化博弈算法(Co-evolutionary Game Algorithm，CGA)对模型进行求解。在此基础上，考虑分布式能源随机性影响建立了基于不满意度的动态优化子模型，对协同演化博弈算法进行动态调整。对某一欧洲典型微网接入 IEEE 33 配电网结构的系统进行仿真，并且与传统的多目标优化方法进行对比。结果表明，最终优化稳定策略可以使微网和配电网整体达到最佳运行状态，证明了所提模型和算法的有效性和优越性。

微网；配电网；协同演化博弈算法；动态优化

0 引言

随着全球能源环境问题日益凸显，清洁能源和可再生能源利用的呼声日渐高涨[1-2]。与此同时，微网包含风电、光伏电池等分布式电源(Distributed Generation，DG)，为解决可再生能源的综合利用提供了有效手段[3]。微网接入配电网运行可以增加供电灵活性，丰富了传统电网运行方式并且可以实现节能减排[4-6]，已经成为电网的一个重要组成部分。未来在微网逐渐普及的情况下，微网自身的能量优化和配电网与微网的合理互动调度将成为必须研究的理论和实际问题。

在微网能量优化方面，文献[7]针对微网运行中风力机、光伏的不确定性及负荷的波动性，提出了基于机会约束规划的经济运行模型，以一定置信水平下满足备用作为可靠性概率约束。文献[8]研究含电动汽车和光伏储能的微网能量管理问题，提出了兼顾光伏出力、电动汽车功率、储能状态和电价划分的能量管理策略。文献[9]通过电动汽车、储能单元以及可中断负荷的能量优化管理，平抑微网与配电网公共联络线上的功率波动，实现经济和稳定运行。

上述工作从不同角度解决了微网能量优化问题，但没有考虑微网和配网的互动运行。在此基础上，文献[10]研究微网与电网协调运行模式，提出了一种基于互动电网的含多微网电力系统的调度模式，建立了微网与电网联合调度模型。文献[11]考虑配电网经济性，建立了基于价格差异与时间贯序权重的智能配电网两阶段快速调度决策模型。文献[12]考虑多微网协同运行情况，分析配电网和微网的经济利益，建立了微网和配电网随机双层随机调度模型，并提出协调控制策略。文献[13]建立了微网和配电网的互动调度模型，并且考虑负荷需求侧管理，对电网运行成本进行优化。

上述文献对微网和配电网的互动调度只从双方经济性出发，没有考虑微网出力对配电网运行的影响。事实上，微网的出力会影响配电网运行的稳定性和安全性，配电网对微网的调度需求也会影响微网的经济性，两者的优化运行是相互约束、相互影响的。所以，在制定调度计划时，需要整合考虑微网和配电网的运行效益。

本文研究微网和配电网互动运行时相互影响的情况，通过分析配电网和微网的运行效益，将其作为虚拟博弈参与者建立了模型。配电网模型以网损和电压稳定水平为优化效益目标，决策微网出力；微网模型以运行成本为优化效益目标，决策微网中各分布式能源的出力；其中公共联络点(Point of Common Coupling，PCC)功率由微网和配电网共同决策。采用模糊数学的方法，对效益函数进行隶属化处理。结合演化博弈理论和协同进化算法，提出了一种协同演化博弈算法，对模型进行求解。在此基础上，考虑分布式能源随机性影响建立了基于不满意度的动态优化子模型，对协同演化博弈算法进行动态调整。仿真结果证明了所提算法的有效性和优越性。

1 模型设计

在微网和配电网互动运行时，两者之间存在能量交互，有密不可分的关系。一方面，配电网对微网进行能量调度，对微网经济性产生影响；另一方面，微网出力也对配电网运行的安全性和稳定性存在影响，双方的利益存在一定冲突。应用博弈理论，可以使具有一定的利益冲突的微网和配电网作为博弈参与者，并且使它们依照一定数学规则进行博弈优化[14]，其优化结果取决于它们各自的效益目标。在此基础上，采用合适的算法可以寻找到所有博弈参与者达到整体最优的稳定策略。因此，配电网与微网可以通过博弈共同制定调度策略，具体的虚拟博弈参与者如图1。

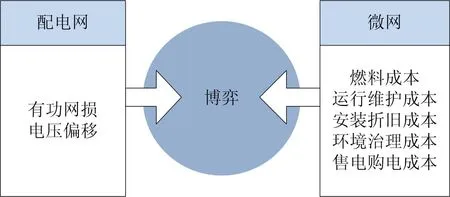
图1 配电网和微网博弈结构Fig. 1 Game structure of distribution network and microgrid

1.1 配电网优化模型

1.1.1 效益函数

配电网的决策变量为微网与配电网公共连接点的传输功率，以有功网损为目标，节点电压质量为罚函数，具体效益函数如式(1)。

式中：lossP 为配电网有功网损为节点电压质量；为各节点电压质量的罚因子。

电压质量 VD 采用整个配电网节点电压偏移量表示，定义如式(2)。式中：n是配电网节点个数；Vi为节点i的电压，电压基准值为 1，则为该节点电压偏移量，[ ]表示向左取整。设即电压偏移范围为(为额定电压)，于是当电压偏移超过 0.05 时，效益函数值会突然增大，进一步增加了非可行解的淘汰率。

1.1.2 约束条件

配电网优化模型的约束主要包括潮流方程约束、联络线容量限制和微网输送功率能力约束。

1) 潮流约束

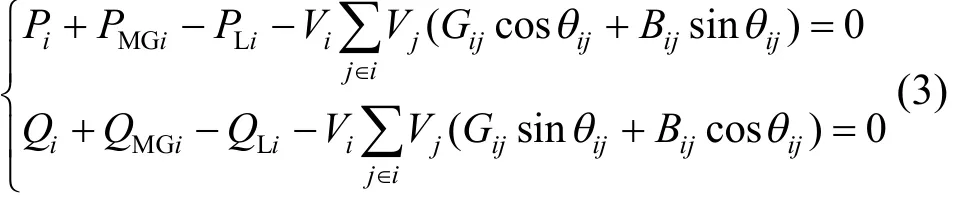
式中：iP、iQ 分别为节点i发电机发出的有功功率和无功功率；分别为节点i微网输送的有功功率和无功功率；分别为节点i负荷的有 功功率和无功 功率和分别 为节点i和 节点 j的电压幅值；Gij和 Bij分别为线路 ij的电导和电纳；qij为节点i和节点 j电压的相角差，

2) 联络线容量限制

3) 微网输送功率能力约束

微网输送功率能力由 DGs发电预测曲线和负荷预测曲线估算得出。

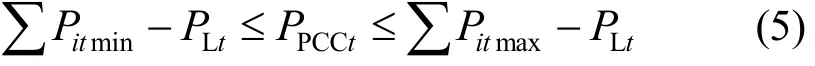
1.2 微网优化模型

1.2.1 效益函数

微网的决策变量是微网中分布式能源的出力，以及微网与配电网 PCC 传输功率，以整个微网的运行成本为目标，具体效益函数为式(6)。

1.2.2 约束条件

微网运行的约束条件包括系统功率平衡约束、分布式电源出力约束和微型燃气轮机爬坡约束等限制。

1) 功率平衡约束

式中：LtP 为 t 时刻微网的负荷需求；itPå 为 t 时刻微网中所有分布式电源出力之和。

2) 分布式电源出力约束

3) 微型燃气轮机爬坡率约束

增负荷时，有

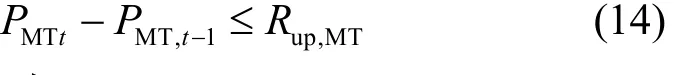
减负荷时，有

4) 联络线容量限制同配电网。

1.3 模型模糊处理

由于微网和配电网的效益目标性质不同，无法直接使两者进行博弈，故本文采用模糊数学来处理效益函数，使其成为统一数值以便于比较博弈后的优化程度。首先求出微网和配电网效益目标在各自约束条件下的最优解，再利用这些最优解将各自的效益函数模糊化。

模糊数学是用精确的数学方法表现和处理实际客观存在的模糊现象，要达到此目的，首先要确定隶属度函数 u。u 的大小反映了优化程度，u=1 代表优化程度最好，而 u=0 代表优化程度最差。通过比较分析，本文选用降半 Γ 形分布[8]。对于上述效益函数，采用降半Γ形分布的隶属度函数为

2 基于协同演化博弈算法(CGA)的模型求解

2.1 协同演化博弈算法

演化博弈理论是博弈论的一个分支，它在假定演化的变化是由群体内的自然选择引起的基础上，通过具有频率依赖效应的选择行为进行演化以搜索演化稳定策略，并研究演化的过程[15]。协同进化算法在传统进化算法的基础上引入生态系统的概念，将待求解的问题映射为相互作用、相互影响的各物种组成的生态系统，以生态系统的进化来达到问题求解的目的[16]。本文结合演化博弈理论和协同进化算法，提出了一种协同演化博弈算法来求解模型，实验结果说明其具有良好的性能。

在协同演化博弈算法中，微网和配电网作为博弈参与者，分别生成两个种群记为 P1 和 P2，p1和p2为初始群体中的种群分布概率。每个种群中有一定个数的个体，个体记录决策向量的同时还记录了所属的种群。P1、P2 分别以 u1、u2为效益目标。种群博弈结构如图2所示。

图2 种群博弈结构Fig. 2 Game structure of populations

在演化博弈中，每个个体都是随机地从群体中抽取并进行重复博弈，假设每个博弈的参与个体只具有有限的理性。算法借鉴了演化博弈的思想和选择机制，当群体中两个个体相遇时，它们为了同一份资源进行博弈。设效益最大化博弈问题中两个个体和相遇并进行博弈，x 所得支付函数如式(17)。

在演化算法的每一代，随机挑选成对的个体进行若干次重复博弈。当所有博弈完成之后，由个体x参与的 Ng次博弈所得到的平均支付作为个体x的适应度 F(x)：

值得注意的是，在演化博弈开始前各个种群在群体中的分布概率 pi是可以调整的，而最终达到的演化稳定策略在很大程度上与初始种群分布是相关的，这就可以通过外部决策者的不同需求使微网和配电网间的博弈地位达到灵活的变化，最终得到最佳调度决策。

2.2 基于最大不满意度的动态优化子模型

由于微网中的风力机和光伏电池受环境气候影响极大，为了防止其随机性和波动性对配电网运行产生过大影响[17]，有必要考虑由于随机性导致的稳定决策满意度，从而在演化博弈时对算法参数作出动态调整。

式中，ws为场景对应的概率权重；为微网实际出力与调度决策出力的差距；l为单位惩罚成本；设该次调度决策下的微网运行总成本为最大不满意度比例为则根据下面两种关系，对种群分布概率作适当调整：

在演化的每一代，在考虑分布式能源随机性影响的基础上，通过动态优化子模型计算不满意度，从而调整两个种群的分布概率使微网和配电网的博弈地位进行变化，再进行下一次演化，最终可以得到最佳稳定调度决策。

2.3 优化流程

动态协同演化博弈算法具体流程图如图3所示，求解步骤如下。

步骤 1：输入原始数据和参数，设置种群分布概率，随机生成初始群体，生成初始可行策略组合。

步骤 2：随机挑选群体中两个个体进行博弈，按照式(17)分别计算个体所得支付。

步骤 3：重复步骤 2直至博弈次数达到重复博弈最大次数。

步骤 4：根据式(18)计算个体适应度。

步骤5：生成随机场景，计算本代演化调度决策的不满意度。如果不满意度超过最大承受值，则动态调整种群分布概率。

步骤6：两个种群分别进行选择、交叉和变异，生成下一代。

步骤 7：重复 2~6 直到整个群体达到演化稳定或达到最大演化代数。

图3 算法流程图Fig. 3 Flowchart of algorithm

3 算例分析

3.1 仿真系统概述

本文将某一欧洲典型微网结构[18]接入 IEEE 33配电网结构的30节点进行仿真，系统图如图4所示。微网系统中，风力机(Wind Turbine，WT)和光伏电池(Photovoltaic，PV)的安装台数分别为 5 台和 2 台，总装机容量分别为 500 kW 和 300 kW，微型燃气轮机(Micro-turbine，MT)的容量为 500 kW，燃料电池(Fuel Cell，FC)容量为 150 kW，各分布式能源的装机容量和安装成本[19]如表1 所示；各分布式能源的运行维护、燃料成本参数和污染物排放系数见文献[20]；配电网与微网实时交易电价[21]如表2 所示；风力机和光伏电池的功率预测曲线如图5所示；微网负荷的预测曲线如图6所示。

需要说明的是，选取配电网中其他的节点连接微网并不影响本文所得结论。

图4 配电网-微网结构图Fig. 4 Structure of the distribution-microgrid network

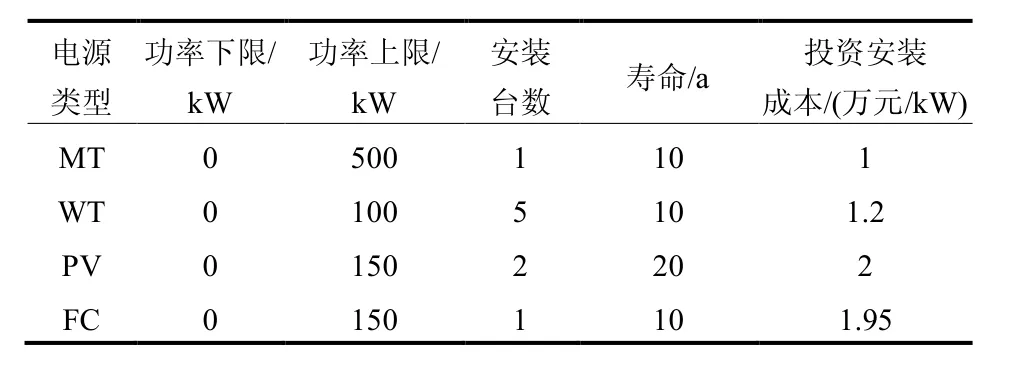
表1 分布式电源运行参数Table 1 Operating parameters of distributed generations

表2 实时电价Table 2 Spot price

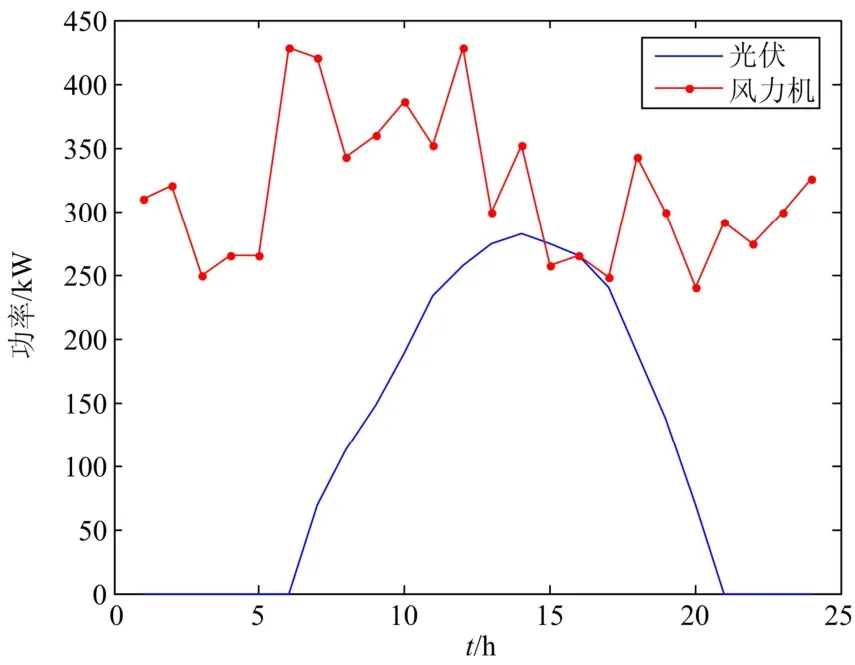
图5 光伏与风力机输出功率预测曲线Fig. 5 Output power prediction of PV and WT

图6 微网负荷功率预测曲线Fig. 6 Power prediction of load

3.2 优化结果

3.2.1 不同种群分布概率对演化博弈结果的影响

暂不考虑最大不满意度对种群分布概率的动态影响，通过人为选择不同的初始种群分布概率，分别进行演化博弈，得到上述系统优化结果变化如图7所示。

图中横坐标表示配电网所属种群1的分布概率p1，即以 u1为效益目标的种群在整个群体中所占的比例，取值为从 0 到 1，间隔为 0.05。实验均重复10 次，图中标出的点为 10 次重复实验的平均结果。从图中可以看出，随着 p1的增大，最终演化稳定决策下的配电网效益隶属度 u1的数值呈上升趋势，而微网效益隶属度 u2的数值呈下降趋势。这是由于在CGA 算法中，当群体中以 u1为效益目标的个体数量增多时，这些个体在随机的博弈过程中容易和同一种群的其他个体进行博弈，间接增大了它们的适应度，使 u1比 u2更具优势，从而导致最终演化博弈结果偏向于 u1。

图7 种群分布概率对优化策略结果影响Fig. 7 Impact of the population probability on optimal result

上述结果表明，最终达到的演化稳定策略在很大程度上与初始种群分布是相关的。种群所占比例越大，其对应效益函数的优化程度越好。于是，通过外部决策者的不同需求可以使微网和配电网的博弈地位达到灵活变化，最终得到最佳调度决策。

3.2.2 微网和配电网博弈优化结果

考虑分布式能源随机性的影响，通过基于最大不满意度的动态优化子模型对每一代演化种群的分布概率进行动态调整，由此调整微网和配电网的博弈地位，能够在进一步保证系统稳定性的情况下得到微网和配电网的更加准确的最佳运行决策。图8~图9和表3为微网和配电网进行动态博弈优化后达到整体最佳运行状态和它们分别达到最优运行状态的效益情况对比。

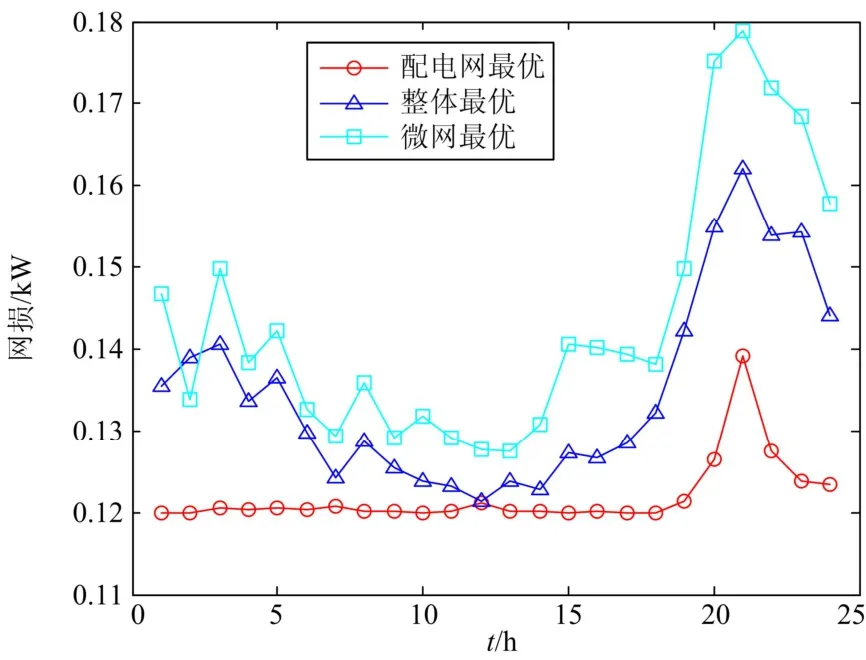
图8 不同情况网损对比Fig. 8 Network loss under different situations

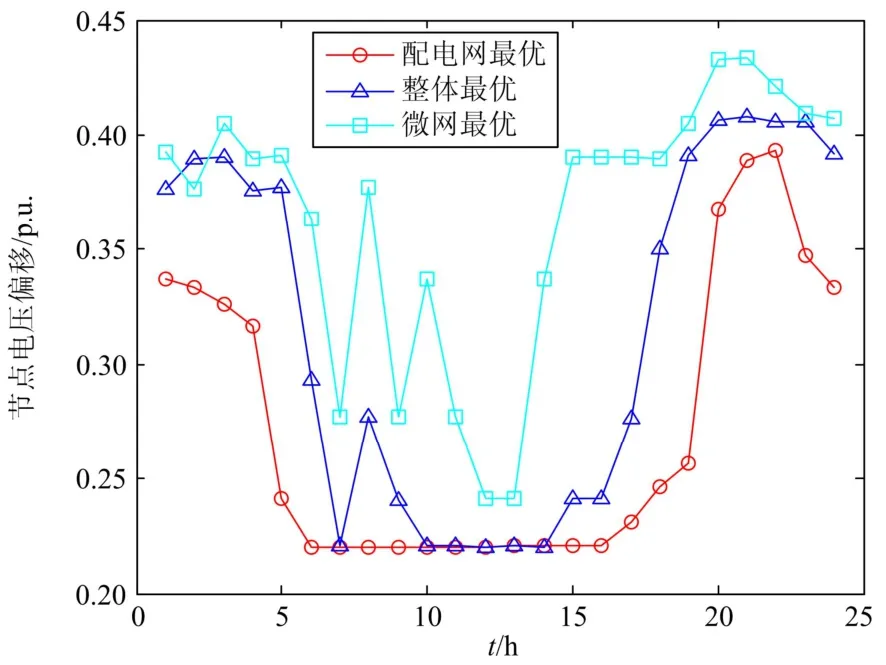
图9 不同情况电压偏移对比Fig. 9 Network voltage offset under different situations

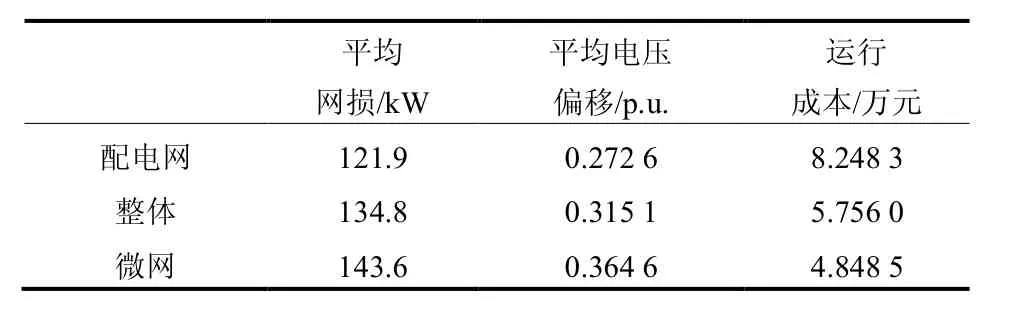
表3 不同情况效益对比Table 3 Benefit under different situations

图8~图9为上述不同情况下配电网的网损和电压偏移情况，表3给出了配电网网损、电压偏移平均值和微网的经济效益情况。通过比较可以明显看出，在配电网达到最优运行状态时，一天的平均网损为 121.9 kW，平均电压偏移为 0.272 6 p.u.，两者都很小，配电网能够安全稳定地运行；而微网的经济效益并不理想。在微网达到最优运行状态时，由于仅考虑了自身成本而未考虑配电网运行的稳定性，运行成本为 4.848 5 万元，达到很好的经济效益；但配电网的平均网损和电压偏移较前一种情况都有较大的提高。而在考虑微网和配电网整体最佳运行状态的情况下，配电网一天的平均网损、平均电压偏 移 和 微 网 的 运 行 成 本 分 别 为 134.8 kW 、0.315 1 p.u.和 5.756 0 万元，均居于前两种状态之间，是考虑了双方利益的折中值，使得微网和配电网都达到相对较好的运行状态。

考虑最大不满意度动态博弈优化的系统最佳运行状态下微网各分布式电源出力情况如图10 所示。为对比分析不同情况的影响，图中也标出了微网和配电网分别达到最优运行状态时 PCC 的功率输出。

由图中可以看出，系统整体最优时，微网进行优化时在一定程度上考虑了配电网的效益，在满足自身经济效益的同时，PCC 输出功率会尽量满足配电网所需最优功率。但此时 MT和 FC 输出功率需要不断调整，尤其是MT的输出总体上不断增加，因此微网的运行成本也会相应增加，该成本的增加主要是MT的燃料成本和排放成本增加导致。

图10 整体最优时调度情况Fig. 10 Scheduling of overall optimization

CGA 算法中配电网和微网各自效益目标变化趋势如图11 所示。图中可以看出微网和配电网经过动态演化博弈过程，最终可以达到双方都比较满意的运行状态，并且达到稳定。

图11 效益隶属度变化趋势Fig. 11 Variation trend of benefit membership

如果把微网和配电网整体效益优化看作一般多目标优化问题，可以求得其 Pareto 最优解集。为了对比本文方法算得的优化决策与一般多目标优化的 Pareto 最优解集，同样考虑配电网的网损、电压偏移和微网的运行成本，采用多目标遗传算法求得其 Pareto 最优解集和本文算得的 CGA 优化解如图12所示。

图12 Pareto 最优解和 CGA 解Fig. 12 Pareto optimal solutions and CGA solution

从图中可以看出，Pareto 最优解集中，一般有很多个解，要从这些解里面选择一个合适的解使微网和配电网都达到相对最好的利益还需要进一步处理；而采用 CGA 可以通过微网和配电网演化博弈进行动态优化，最终得到两者整体最优的唯一稳定策略。通过 CGA 算法得到的最优决策贴近 Pareto前沿，可以表明其准确性；但是所得最优决策并没有完全与 Pareto 前沿重合，是因为考虑了分布式能源随机性动态影响的结果。CGA算法跟传统多目标优化算法相比，所得的最优决策只有一个，具有明显优越性；此外，由于考虑了分布式能源随机性影响，所得策略在实际运行情况下也能够获得较好的效益，具有一定的鲁棒性。

以上结果表明，通过将微网和配电网作为博弈参与者进行多轮演化博弈，并且考虑分布式电源随机性的影响动态调整概率分布参数，最终可以得到一个合理的最优策略，使得微网和配电网达到整体最优运行状态。

4 结论

本文整合考虑微网和配电网互动运行时的效益，研究其相互影响情况，建立了效益模型，并对效益函数进行隶属化处理。结合演化博弈理论和协同进化算法，提出了一种协同演化博弈算法，对隶属化后的模型进行求解。在此基础上，考虑分布式能源随机性影响建立了基于不满意度动态优化子模型，对协同演化博弈算法进行动态调整。结果表明，本文所提方法可以使微网和配电网通过双方各自效益最大化进行博弈，并基于不满意度进行动态优化调整，最终稳定策略可以使微网和配电网整体达到最佳运行状态，保证配电网稳定运行的同时保持微网的经济性。

考虑多个微网接入配电网后，多微网间以及微网与配电网间的协调互动优化是进一步研究的方向。

[1]杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70. YANG Xinfa, SU Jian, LÜ Zhipeng, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70.

[2]黎静华, 文劲宇, 潘毅, 等. 面向新能源并网的电力系统 鲁 棒 调 度 模 式 [J]. 电 力 系 统 保 护 与 控 制 , 2015, 43(22): 47-54. LI Jinghua, WEN Jinyu, PAN Yi, et al. Robust dispatching mode of electrical power system to cope with renewable energy power[J]. Power System Protection and Control, 2015, 43(22): 47-54.

[3]周龙, 齐智平. 微电网保护研究综述[J]. 电力系统保护与控制, 2015, 43(13): 147-154. ZHOU Long, QI Zhiping. A review of the research on microgrid protection development[J]. Power System Protection and Control, 2015, 43(13): 147-154.

[4]FANG X, MISRA S, XUE G, et al. Smart grid - the new and improved power grid: a survey[J]. IEEE Communications Surveys & Tutorials, 2012, 14(4): 944-980.

[5]马艺玮, 杨苹, 王月武, 等. 微电网典型特征及关键技术[J]. 电力系统自动化, 2015, 39(8): 168-175. MA Yiwei, YANG Ping, WANG Yuewu, et al. Typical characteristics and key technologies of microgrid[J]. Automation of Electric Power Systems, 2015, 39(8): 168-175.

[6]沈沉, 吴翔宇, 王志文, 等. 微电网实践与发展思考[J].电力系统保护与控制, 2014, 42(5): 1-11. SHEN Chen, WU Xiangyu, WANG Zhiwen, et al. Practice and rethinking of microgrids[J]. Power System Protection and Control, 2014, 42(5): 1-11.

[7]刘方, 杨秀, 时珊珊, 等. 基于序列运算的微网经济优化调度[J]. 电工技术学报, 2015, 30(20): 227-237. LIU Fang, YANG Xiu, SHI Shanshan, et al. Economic operation of microgrid based on sequence operation[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 227-237.

[8]苏粟, 蒋小超, 王玮, 等. 计及电动汽车和光伏-储能的微网能量优化管理[J]. 电力系统自动化, 2015, 39(9): 164-171.SU Su, JIANG Xiaochao, WANG Wei, et al. Optimal energy management for microgrids considering electric vehicles and photovoltaic-energy storage[J]. Automation of Electric Power Systems, 2015, 39(9): 164-171.

[9]张明锐, 陈洁, 杜志超, 等. 考虑交互功率控制的微网经 济 运 行 [J]. 中 国 电 机 工 程 学 报 , 2014, 34(7): 1013-1023. ZHANG Mingrui, CHEN Jie, DU Zhichao, et al. Economic operation of micro-grid considering regulation of interactive power[J]. Proceedings of the CSEE, 2014, 34(7): 1013-1023.

[10]艾欣, 许佳佳. 基于互动调度的微网与配电网协调运行 模式 研究 [J]. 电 力系 统保 护与 控制, 2013, 41(1): 143-149. AI Xin, XU Jiajia. Study on the microgrid and distribution network co-operation model based on interactive scheduling[J]. Power System Protection and Control, 2013, 41(1): 143-149.

[11]江润洲, 邱晓燕, 李丹. 基于多代理的多微网智能配电 网 动 态 博 弈 模 型 [J]. 电 网 技 术 , 2014, 38(12): 3321-3327. JIANG Runzhou, QIU Xiaoyan, LI Dan. Multi-agent system based dynamic game model of smart distribution network containing multi-microgrid[J]. Power System Technology, 2014, 38(12): 3321-3327.

[12]WANG Z, CHEN B, WANG J, et al. Coordinated energy management of networked microgrids in distribution systems[J]. IEEE Transactions on Smart Grid, 2015, 6(1): 45-53.

[13]FATHI M, BEVRANI H. Statistical cooperative power dispatching in interconnected microgrids[J]. IEEE Transactions on Sustainable Energy, 2013, 4(3): 586-593.

[14]WANG Y, SAAD W, HAN Z, et al. A game-theoretic approach to energy trading in the smart grid[J]. IEEE Transactions on Smart Grid, 2014, 5(3): 1439-1450.

[15]武英利, 张彬, 闫龙, 等. 基于演化博弈的海上风电投资策略选择及模型研究[J]. 电网技术, 2014, 38(11): 2978-2985. WU Yingli, ZHANG Bin, YAN Long, et al. Research and modeling of evolutionary game based selection of investment strategies for offshore wind farm[J]. Power System Technology, 2014, 38(11): 2978-2985.

[16]陈皓勇, 王锡凡, 别朝红, 等. 协同进化算法及其在电力 系 统 中 的 应 用 前 景 [J]. 电 力 系 统 自 动 化 , 2004, 27(23): 94-100. CHEN Haoyong, WANG Xifan, BIE Zhaohong, et al. Cooperative coevolutionary approaches and their potential applications in power systems[J]. Automation of Electric Power Systems, 2004, 27(23): 94-100.

[17]沈鑫, 曹敏. 分布式电源并网对于配电网的影响研究[J]. 电工技术学报, 2015, 30(1): 346-351. SHEN Xin, CAO Min. Research on the influence of distributed power grid for distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 346-351.

[18]PAPATHANASSIOU S, HATZIARGYRIOU N, STRUNZ K. A benchmark LV Microgrid for steady state and transient analysis[C]// Proceedings of the Cigre Symposium on Power Systems with Dispersed Generation, Athens, April, 2005.

[19]钱科军, 袁越, 石晓丹, 等. 分布式发电的环境效益分析[J]. 中国电机工程学报, 2008, 28(29): 11-15. QIAN Kejun, YUAN Yue, SHI Xiaodan, et al. Environmental benefits analysis of distributed generation[J]. Proceedings of the CSEE, 2008, 28(29): 11-15.

[20]丁明, 张颖媛, 茆美琴, 等. 包含钠硫电池储能的微网系统经济运行优化[J]. 中国电机工程学报, 2011, 31(4): 7-14. DING Ming, ZHANG Yingyuan, MAO Meiqin, et al. Economic operation optimization for microgrids including Na/S battery storage[J]. Proceedings of the CSEE, 2011, 31(4): 7-14.

[21]CHEN J, YANG X, ZHU L, et al. Microgrid economicoperation and research on dispatch strategy[C]// Power Engineering and Automation Conference (PEAM), 2012, 1(1): 1-6.

(编辑 魏小丽)

Dynamic optimization of microgrid and distribution network based on co-evolutionary game algorithm

XU Yiting1, AI Qian1, HU Jiansheng2
(1. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. XJ Group Corporation, Xuchang 461000, China)

Microgrid and distribution network have mutual influences and constraints when interactive operation. Thus, it is necessary to integrate interests of microgrid and distribution network together in order to benefit the entire system. Microgrid and distribution network, as two objectives that need to be optimized at the same time, have some conflicts of interests. The interaction of microgrid and distribution network is studied when interactive operation to analyze their operation benefits respectively. The benefit objectives are modeled as virtual game participants to establish models and fuzzy mathematics method is applied to generalize the benefit functions to membership. In combination with evolutionary game theory and cooperative co-evolutionary algorithm, a co-evolutionary game algorithm is proposed to solve the problem. Then, a maximum dissatisfaction based dynamic optimal sub-model considering the randomness of distributed energy is established to make dynamic adjustments in co-evolutionary game algorithm. A typical Europe microgrid connected with IEEE 33 distribution network is simulated and a simulation with multi-objective optimization method is also carried out for comparison. The results show that the final optimal stable strategy allows the entire microgrid and distribution network to achieve the best operation, thus the effectiveness and superiority of the proposed model and algorithm are proved.

This work is supported by National Natural Science Foundation of China (No. 51577115).

microgrid; distribution network; co-evolutionary game algorithm; dynamic optimization

10.7667/PSPC151702

：2015-11-04

徐意婷(1991-)，女，硕士研究生，研究方向为分布式发电，微网能量优化 ，微网和配电网协调运行 ；E-mail: millyx@sjtu.edu.cn

艾 芊(1969-)，男，博士，教授，主要研究领域为电能质量、人工智能以及在电力系统中的应用、电力系统元件建模、分布式发电与微电网等。

胡剑生(1979-)，男，工程师，主要研究方向为新能源发电系统控制及嵌入式技术。

国家自然科学基金项目(51577115)