基于双目标时变交集的电池储能改善风电场出力控制

王境彪，李 江，胡立强，晁 勤，饶成诚，李泽燃，殷志敏，杨 扬，任 娟

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.国网湖南省电力公司衡阳供电分公司，湖南 衡阳 421001；3.国网新疆电力公司昌吉供电公司，新疆 昌吉 831100；4.新疆军区工程环境质量监督站，新疆 乌鲁木齐 830002；5.国网湖南省电力公司检修公司，湖南 长沙 410004；6.国网辽宁省电力有限公司盘锦供电公司，辽宁 盘锦 124010；7.国网浙江省电力公司湖州供电公司，浙江 湖州 313000；8.国网新疆电力公司经济技术研究院，新疆 乌鲁木齐 830000)

基于双目标时变交集的电池储能改善风电场出力控制

王境彪1,2，李 江3，胡立强4，晁 勤1，饶成诚5，李泽燃6，殷志敏7，杨 扬7，任 娟8

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.国网湖南省电力公司衡阳供电分公司，湖南 衡阳 421001；3.国网新疆电力公司昌吉供电公司，新疆 昌吉 831100；4.新疆军区工程环境质量监督站，新疆 乌鲁木齐 830002；5.国网湖南省电力公司检修公司，湖南 长沙 410004；6.国网辽宁省电力有限公司盘锦供电公司，辽宁 盘锦 124010；7.国网浙江省电力公司湖州供电公司，浙江 湖州 313000；8.国网新疆电力公司经济技术研究院，新疆 乌鲁木齐 830000)

为了抑制风电随机波动和提高风电超短期预测精度，提出了一种基于此双目标时变交集的电池储能控制方法。首先，分别制定了抑制风电波动、提高风电预测精度的单一控制域及此双目标的交集联合控制域，并在考虑两种单一控制目标的时间尺度不同后，制定了随时间变化的双目标交集联合控制域。在此基础之上，结合储能运行约束条件确定了最终的电池储能改善风电场出力控制策略。其次，首次建立了基于越限比和越限相对均值的波动与预测精度评估指标并形成了双目标综合评估体系。最后，应用某风电场实际出力数据，分别在采用神经网络时间序列和差分自回归滑动平均(ARIMA)两种预测模型的前提下，考虑电网对风电波动忍受度和超短期预测误差忍受度的三种大小关系，通过计算波动量总和与均方根误差验证了所建立评估指标的有效性，同时证实了应用该控制策略的电池储能系统能够同时达到抑制风电随机波动和提高风电超短期预测精度两个目标。

双目标时变交集；抑制波动；超短期预测；电池储能；越限比和越限相对均值

0 引言

风力发电作为最成熟的可再生能源发电技术之一，具有无污染、投资周期短等优点，近年来发展迅猛[1-3]。然而，高渗透率的风电接入电网时，风电的随机波动性与预测的不确定性将恶化电网调频环境，加剧系统峰谷差，迫使系统增加备用容量和调频调峰容量，给电网电压频率带来巨大冲击。受制于目前电网的强壮能力，为保证系统的稳定与安全，调度部门不得不常常决策风电场弃风运行，极端情况下甚至切除风电场[4-9]。

储能技术的发展给风能利用的这些问题提供了一种革命性的解决方案。电池储能系统具有容量大、响应速度快、安装灵活等优点，在电力系统中具有广阔的应用前景[9-10]。对此，很多专家学者提出，利用储能的充放电特征，对风电进行“削峰填谷”以抑制其随机波动，或减小风电的预测误差以提高预测精度。文献[11-13]采用了各种方法、策略、模型对储能进行控制以达到平抑风电等可再生能源波动的目标，如利用双层控制模型检索专家信息库、有源并联式混合储能系统(APHESS)、小波分解等；文献[14]论证了利用储能装置提高风电出力预测精度的可行性。文献[15]通过高通滤波器结合模糊控制规则优化混合储能SOC达到提高风出力预测精度的目的，文献[16]研究当利用储能提高风出力预测精度时，通过SOC控制优化其充放电行为，达到合理配置储能容量的目的。但是以上研究都仅限于对储能系统用于抑制波动和提高精度的单目标控制，且缺乏有效直观的评估指标。然而，现阶段风电并网所面临的问题却表现出多样性与复杂性。

为了抑制风电随机波动和提高风电超短期预测精度，提出了一种基于此双目标时变交集的电池储能控制方法。通过制定双目标时变交集联合控制域并结合储能运行约束条件确定了电池储能改善风电场出力的控制策略，建立了基于越限比和越限相对均值的波动与预测精度评估指标并形成了双目标综合评估体系。应用某风电场实际出力数据，分别在采用神经网络时间序列和差分自回归滑动平均(ARIMA)两种预测模型的前提下，考虑电网对风电波动忍受度和超短期预测误差忍受度的三种大小关系，验证了所建立评估体系的有效性，同时证实：采用了该控制策略的电池储能系统确实能够同时达到抑制风电随机波动和提高风电超短期预测精度两个控制目标。

1 改善风电场出力的双目标单一及其交集联合控制域制定

当前风电并网所面临的问题表现出多样性与复杂性，其中如何抑制风电波动与提高风电预测精度引起了极大的研究热度。本文所提出的双目标即是抑制风电波动与提高风电超短期预测误差。

1.1 抑制风电随机波动和提高风电超短期预测精度的单一控制域制定

1.1.1 抑制风电随机波动的单一控制域制定

受制于电网的稳定裕度，并网运行风电场输出功率波动(Fluctuation)需满足式(1)。

由波动允许上下限构成了一条波动允许功率带(波动带)，其带宽恒为

当风电场出力不满足式(1)时，若风电实际出力在波动带以内往上越过波动上限，储能充电，多余的电能存入储能设备；若其实际出力在波动带以内往下越过波动下限，储能放电，等效增大风电出力，保证风储合成出力位于波动允许上下限内，达到利用储能的充放电特征对风功率进行“削峰填谷”，抑制风电波动的目的，如图1所示。

图1 风电随机波动示意图Fig. 1 Schematic diagram of wind power fluctuation

因此，本文认为储能用于抑制风电波动时，用波动带作为储能的控制目标域，即

1.1.2 提高风电短期预测精度单一控制域制定

与抑制风功率波动类似，风电场出力应位于短期预测误差(Prediction)允许的范围内，如式(2)。

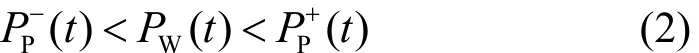
当风电场出力不满足式(2)时，若风电实际出力从误差带内往上越过风误差上限，储能充电，反之，若风电实际出力从误差带内往下越过风误差下限，储能放电。两种情况下，储能都是通过自身的功率吞吐，调整风储合成出力曲线逼近风电超短期预测曲线，达到减小预测误差，提高预测精度的作用，如图2所示。

图2 风电预测误差波动示意图Fig. 2 Schematic diagram of prediction error of wind power

因此，本文认为储能用于提高风电超短期预测精度时，由预测带作为储能的控制目标域，即

1.2 抑制风电随机波动与提高风电超短期预测精度的交集联合控制域制定

当储能工作以同时达到抑制风电随机波动与提高风电超短期预测精度两个控制目标时，需考虑1.1.1 节中的波动带和 1.1.2 节中的预测带之间的关系。本文将这种关系归纳总结为两者是否存在交集，通过对两者交集的分析获得双目标交集联合上下限(Dual Targets Intersection Combined Upper-lower limit，DTICULL)，最终制定了储能的双目标交集联合控制域

1.2.1 波动带和预测带存在交集

波动带和预测带存在交集时，可分为两种情况：波动带和预测带有无包含关系。

(1) 有包含关系

(2) 无包含关系

图3 波动带与预测带存在交集示意图Fig. 3 Schematic diagram of intersection between fluctuation band and prediction band

1.2.2 波动带和预测带不存在交集

由 1.1.1 节分析可知，风电场出力在某一个时刻的允许波动范围是与前一时刻有关的，而风电预测值由于预测手段不同，可能造成在在某一个时刻，风电的预测误差很大，造成风电波动带和预测带没有实际交集，如图4所示。当风电实际出力位于：1) ①/⑤/⑥/⑩区域时，式(1)、式(2)均无法满足，储能应该充/放/充/放电；2) ③或⑧区域时，储能若动作，将处于“顾头不顾尾”的状态；3) ②/④/⑦/⑨区域时，即只满足式(2)/(1)/(1)/(2)，储能若尝试动作去满足另一控制目标，则可能造成风电已满足目标濒临破产。本文认为，为在较大程度上利用储能，应当在保证已满足控制目标不破产的前提下尽可能去迎合另一个控制目标。统计大量风电场出力数据表明，风电出力只满足式(2)/(1)/(1)/(2)情况不多见，从简单起见，本文引入一个权重系数 σ(0<σ<1)，用于调和两种控制目标不同时满足的矛盾。此时：当时 ，

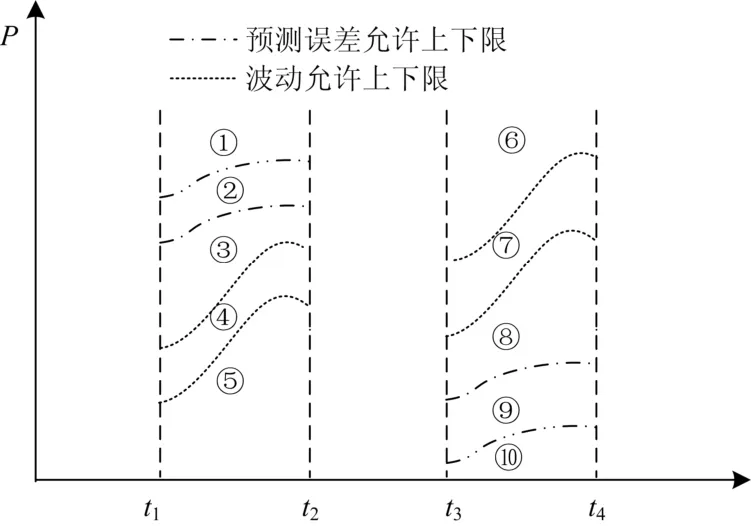
图4 波动带与预测带存在交集示意图Fig. 4 Schematic diagram of no intersection between fluctuation band and prediction band

1.3 抑制风电随机波动与提高风电超短期预测精度的双目标时变交集联合控制域制定

当储能在独立执行抑制风电随机波动与提高风电超短期预测精度两个单一控制任务时，其工作的时间分辨率可能不一样。国网公司已经规定了风电场在任意 10 min 内的波动量和风电场应每 15 min自动向电网调度机构滚动申报超短期功率预测曲线，这就要求风电场上报的后的风电功率预测值与后的实际值之间的误差不能过大。为同时达到两个控制目标，本文取两个单一目标时间分辨率的最大公约数作为储能的工作时间间隔，以起始时刻，在滚动预测时刻的风电出力并根据式(2)计算预测精度的单一控制域，在时刻(j=0, 1, 2,L )滚动计算时刻风电波动的单一控制域。于是获得了双目标时变交集联合控制域，其中：

2 电池储能改善风电场出力控制策略提出

2.1 风-储联合运行系统

在风电场升压站低压汇流母线并联接入电池储能设备，构成风-储联合运行系统，如图5。

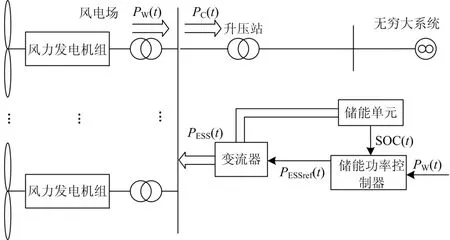
图5 风-储联合系统运行示意图Fig. 5 Schematic diagram of power system containing wind power and BESS

2.2 电池储能控制策略提出

电池储能的充放电深度与功率是影响其寿命的重要因素。为保证风电场运行的经济性，BESS的运行应该受到其额定容量和功率的运行约束。

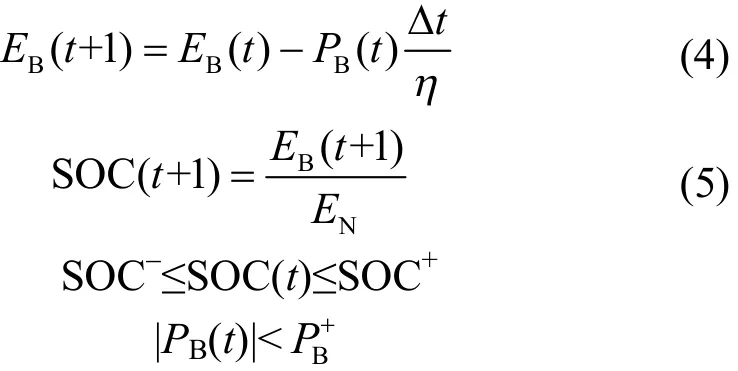
为利用储能达到抑制风电波动与提高风电超短期预测精度的目标，本文提出了以储能自身运行条件为约束，以风电出力是否越出双目标时变交集联合控制域为储能工作判据制定了充放电控制策略如下：

在风—储系统联合运行时，采用滚动规划法，向前滚动执行该控制策略。取双目标时间分辨率的最大公约数(Δt=5 min)作为储能工作的滚动周期。如图6。

3 双目标综合评估体系建立

对于风电场来说，短期内要想将风功率的随机波动完全消除，精确预测风电功率是不可能的。所以将风电波动与预测的误差限制在一定范围内，使电网有足够的能力抵抗风电场出力给自身带来的不确定风险具有重大现实意义

为了评估风功率随机波动与预测误差越出某一范围的状况，本文针对不同容量风电场的出力数据在样本长度不同时的情况，基于越限比与越限相对均值分别建立了随机波动与预测精度评估指标，同时引入了波动量总和(Sum of Fluctuation, SF)均方根误差(RMSE)作为预测精度评估指标的校验指标，形成了双目标综合评估体系。

图6 电池储能控制策略流程图Fig. 6 Flow chart of BESS control strategy

3.1 随机波动评估指标

整个运行期内，采样点时刻风电功率越过波动允许上下限的频次占所有采样时刻的比例。定义为

式中：

整个运行周期T内，采样点时刻风电功率越过波动允许上下限幅值总和的相对平均。定义为

3.2 预测误差评估指标

整个运行期内 T，采样点时刻风电功率越过预测误差允许上下限的频次占所有采样时刻的比例。定义为

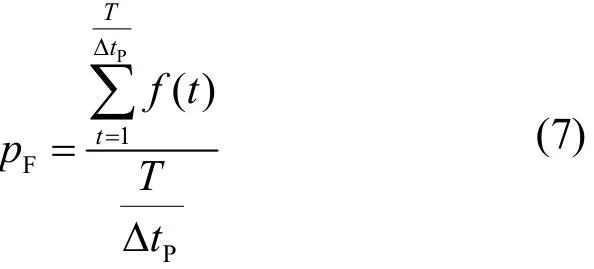
整个运行周期T内，采样点时刻风电功率越过预测误差允许上下限幅值总和的相对平均。定义为

4 仿真验证

本文以图5所示的风储联合系统为模型，验证应用了上述控制策略的电池储能平抑风电随机波动和提高风电超短期预测精度的效果。以某容量为148.5 MW 的风电场在 2012 年 10 月 15 日 00:00 至10 月 24 日 23:55 之间 10 天的实际出力数据(采样间隔为 Δt=5 min，一共 2 880 个采样点)为分析样本，为获得实时预测数值，从第一个点开始，对样本数据等间距(3Δt)采样获得间隔为 15 min 的风电实际出力数据，共 960 个采样点，进而对该时间段内风电出力进行预测，预测周期也为 15 min，获得 960个超短期风电功率预测值。以第一个采样点作为预测和波动计算的的公共起始点，则由 1.3 节可知，对于分析样本的第 y 个采样点，若，则需要按照 1.1.2 节中与计算双目标交集联合控制域，否则以 1.1.1 节波动单一控制域作为双目标交集联合控制域。

在风电的超短期预测中，常用的预测模型总体分为两类，学习模型和统计模型。本文采用学习模型中的神经网络时间序列模型(Neural Net Time Series，NNTS)和统计模型中的差分自回归滑动平均(ARIMA)模型进行风功率超短期预测。神经网络时间序列模型两种预测模型已较为成熟，在此不再赘述。其中神经网络时间序列预测是基于 Matlab2012b中 ntstool工具箱的非线性自回归(NAR)模型完成。图7示出了风电实际与预测出力值。表示出了两种预测模型的预测效果。从表1可以看出，NNTS预测效果要优于 ARIMA。

图7 NNTS 与 ARIMA 预测值Fig. 7 Prediction value by applying NNTS or ARIMA

表1 NNTS 与 ARIMA 预测效果Table 1 Prediction effect by applying NNTS or ARIMA

4.1 风电波动忍受度大于预测误差忍受度

从图8(a)中放大图可以看出，当风电波动忍受度大于预测误差忍受度且采用NNTS进行预测时，i=1364, 1365, 1367, 1368, 1370, 1371, 1373, 1374, 1376, 1377 个采样点， 由于(i-1)|3≠0，第 i 点对应时刻的前 15 min 时刻，不需要向调度部门上报此时刻预测值，故 DTICULL 就是波动上下限；在 j=1366, 1369, 1372, 1375, 1378 个采样点，由于(j-1)|3= 0，故需要根据波动带和预测带是否存在交集确定DTICULL：当 j=1366, 1372 时，波动上下限与预测上 下 限 存 在 交 集 但 不 存 在 包 含 关 系 ，时,且， 所 以时，且所 以。当 j=1369 时，波动上下限与预测上下限存在交集，且存在包含关系，预测上下限包含于波动控制域内，且，所以，当时，出现了波动带与预测带不存在交集的极端情况 ，。此时，采用权重系数σ调和两控制目标的矛盾，双目标交集联合上限向预测带突入半个预测带宽，双目标交集联合下限向波动带突入半个波动带宽。

图8 波动忍受度较大时双目标时变交集联合上下限Fig. 8 DTICULL when endurance of wind power fluctuation is bigger

采用与图8(a)相同的方法分析图8(b)可知，当风电波动忍受度大于预测误差忍受度且采用进行预测时，在个采样点，DTICULL 就是波动上下限，而在 j=1918, 1921, 1924, 1927, 1930 个采样点，则需要根据波动带和预测带是否存在交集确定 DTICULL：当 j=1918, 1927 时，波动上下限与预测上下限存在交集但不存在包含关系，；当和 1930 时，波动上下限与预测上下限存在交集且存在包含关系，预测上下限包含于波动上下限，故统计全部数据表明，采用 ARIMA 模型进行预测时，没有出现波动带与预测带不存在交集的极端情况，采用NNTS 模型预测时，出现共 15 次，占比 1.563%，印证了 1.2.2 节中这种极端情况出现概率很小的论断。

当双目标时变交集联合控制域制定以后，应用上述控制策略的改善风电场出力效果如表2所示，储能 SOC 变化情况如图9。

表2 波动忍受度更大时电池储能工作效果Table 2 BESS work effect when endurance of wind power fluctuation is bigger

图9 波动忍受度更大时电池储能 SOCFig. 9 SOC of BESS when endurance of wind power fluctuation is bigger

从表2中可以看出，投入储能前后：波动越限比 pF和波动越限均值别减小了 2.436%和2.419 kW，波动量总和 SF 减小了 684 MW；采用NNTS/ARIMA 模型进行预测时，误差越限比 pP和误差越限相对均值 VP分别减小了和，均方根误差减小了。以是否投入储能进行纵向比较可以发现，波动越限比和波动越限相对均值的变化趋势与波动量总和变化趋势是一致的，误差越限比和误差越限相对均值两个指标的变化趋势和均方根误差的变化是一致的，投入储能有助于减小风功率超短期预测误差。横向比较采用 NNTS 和 ARIMA 模型两种情况可以看出，未投储能时，NNTS 模型预测效果更好，投入储能时，虽然采用NNTS模型预测的误差经储能修正后的效果仍然更好，但是观察三个指标在两种情况下的差别，可以发现这种差别在减小，储能对于 ARIMA 模型预测后的误差修正程度要更大，这也可以从图9中采用ARIMA预测时储能SOC变化更剧烈得到验证。

从图9 中可以看出，储能 SOC 绝大部分位于[0.1, 0.9]范围内，有助于延长 SOC 的工作。采用NNTS 预测时，储能的充放电功率较采用 ARIMA时起伏小，从另一角度也证明了未投储能时风电实际出力越出预测精度上下限的幅度小，预测精度更高。

4.2 风电波动忍受度小于预测误差忍受度

图10 波动忍受度较小时双目标时变交集联合上下限Fig. 10 DTICULL when endurance of wind power fluctuation is smaller

采用 4.1 节中的方法分析图10 可知，当电网的风电波动忍受度小于预测误差忍受度时，由于波动带宽减小，除了之外的采样点之外，采用NNTS 预测时的第 1366 和个采样点和采用时 的个 采 样 点 ， 其DTICULL 都等于波动上下限。采用 NNTS 时在 j = 1372，1375 和 1378 时的 DTICULL 上下限与 4.1 节中对应点的情况相同。采用 ARIMA 时在 j=1918 和1927 时与 4.1 节中的情况也相同。采用两种预测模型时，双目标带不存在交集的极端情况分别出现 11次和 2 次，占比 1.146%和 0.208%。

应用上述控制策略的电池储能改善风电场出力效果如表3 所示，储能 SOC 变化情况如图11。

表3 波动忍受度更小时电池储能工作效果Table 3 BESS work effect when endurance of wind power fluctuation is smaller

图11 波动忍受度更小时电池储能 SOCFig. 11 SOC of BESS when endurance of wind power fluctuation is smaller

从图11 可以看出，SOC 大部分都位于[0.1, 0.9]以内。

4.3 风电波动忍受度等于预测误差忍受度

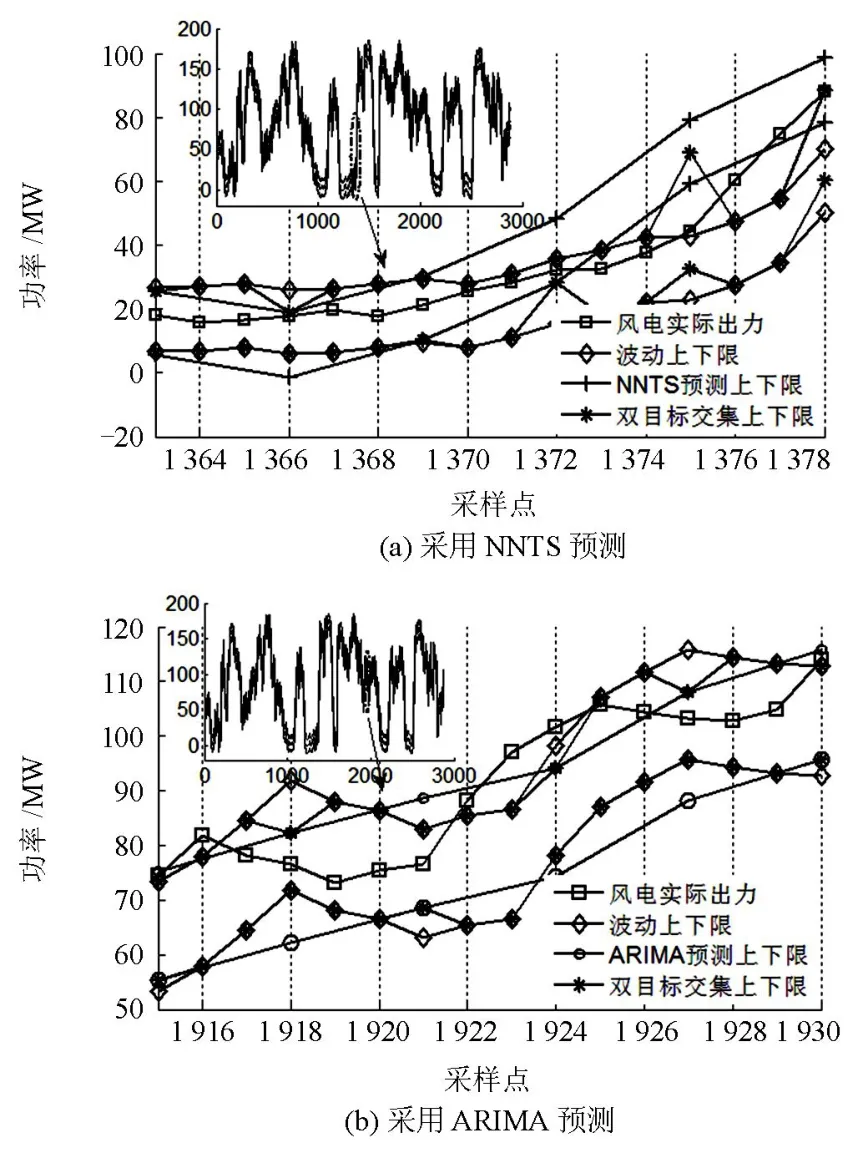
图12 双目标忍受度相同时其时变交集联合上下限Fig. 12 DTICULL when endurance of dual targets is equal

采用 4.1 节的方法并与 4.1 节和 4.2 节对比分析图12 可知，采用 NNTS 模型预测时，确定 DTICULL时与 4.1 节确定时情况完全一样。采用 ARIMA 模型预测的 1918 和 1927 个采样点和 4.1 节、4.2 节对应采样点的 DTICULL 确定情况是相同的，而 j= 1921, 1924 和 1930 时，与 4.1 节和 4.2 节中双目标带存在包含关系而用单一目标上下限就可以确定DTICULL 不同，双目标带之间的关系是存在交集而不存在包含关系：在和 1930 采样点,； 在采 样 点 ，。在两种预测模型下，双目标带不存在交集的极端情况分别为30次和17次，占比为 3.125%和 1.771%。

从图13 可以看出储能 SOC 变化程度比图9 和图11都剧烈。不难推断，这是因为电网对双目标的忍受程度总体降低了。

表4 双目标忍受度相同时电池储能工作效果Table 4 BESS work effect when endurance of dual targets is equal

图13 双目标忍受度相等时电池储能 SOCFig. 13 SOC of BESS when endurance of dual targets is equal

5 结论

本文提出了一种基于抑制风电波动与提高超短期预测精度双目标时变交集的电池储能改善风电场出力控制方法，研究总结如下所述。

1) 建立了抑制风电波动与提高超短期预测精度的各自单一控制域及其交集联合控制域，并在考虑波动时间尺度与预测时间尺度特性不同的情况下制定了双目标时变交集联合控制域。

2) 依据1)中建立的双目标时变交集联合控制域并结合电池储能的运行约束条件制定了电池储能的充放电控制策略。

3) 首次建立了基于越限比和越限相对均值的风电波动与预测精度的评估指标，并以波动量总和与均方根误差作为所建立波动指标和预测指标的校验指标，形成了双目标综合评估体系。

4) 分别在采用神经网络时间序列和差分自回归滑动平均(ARIMA)两种预测模型的前提下，考虑电网对风电波动忍受度和超短期预测误差忍受度的三种大小关系，验证了所建立的评估指标的有效性，纵向比较可以发现，投入储能有助于减小风功率超短期预测误差。横向比较采用 NNTS 和 ARIMA 模型两种情况可以看出，未投储能时，NNTS 模型预测效果更好，投入储能时，虽然采用NNTS模型预测的误差经储能修正后的效果仍然更好，储能对于ARIMA 模型预测后的误差修正程度要更大。

[1]刘世林, 文劲宇, 孙海顺, 等. 风电并网中的储能技术研 究 进 展 [J]. 电 力 系 统 保 护 与 控 制 , 2013, 41(23): 145-153. LIU Shilin, WEN Jinyu, SUN Haishun, et al. Progress on applications of energy storage technology in wind power integrated to the grid[J]. Power System Protection and Control, 2013, 41(23): 145-153.

[2]HAO Zhenghang, LI Shaohua, ZHANG Ailing. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Tehnicki Vjesnik, 2015, 22(1): 43-49.

[3]刘畅, 吴浩, 高长征, 等. 风电消纳能力分析方法的研究[J]. 电力系统保护与控制, 2014, 42(4): 61-66. LIU Chang, WU Hao, GAO Changzheng, et al. Study on analysis method of accommodated capacity for wind power[J]. Power System Protection and Control, 2014, 42(4): 61-66.

[4]程世军, 孟杰, 王晓晖, 等. 风电-储能联合日运行优化调度模型[J]. 电网与清洁能源, 2014, 30(4): 68-72, 80. CHENG Shijun, MENG Jie, WANG Xiaohui, et al. A joint daily operational optimization model for wind power and energy storage devices[J]. Power System and Clean Energy, 2014, 30(4): 68-72, 80.

[5]王小红, 周步祥, 张乐, 等. 基于时变 Copula 函数的风电 出 力 相 关 性 分 析 [J]. 电 力 系 统 及 其 自 动 化 学 报 , 2015, 27(1): 43-48. WANG Xiaohong, ZHOU Buxiang, ZHANG Le, et al. Wind power correlation analysis based on time-variant Copula function[J]. Proceedings of the CSU-EPSA, 2015, 27(1): 43-48.

[6]高玉洁, 张永凯, 李蓉蓉, 等. 计及风电的电力系统检修 备用 容量 评估 及应 用 [J]. 高压电 器, 2015, 51(6): 31-38. GAO Yujie, ZHANG Yongkai, LI Rongrong, et al.Maintenance reserve capacity evaluation and its application considering wind power and maintenance demand uncertainty[J]. High Voltage Apparatus, 2015, 51(6): 31-38.

[7]张宁, 周天睿, 段长刚, 等. 大规模风电场接入对电力系统调峰的影响[J]. 电网技术, 2010, 34(1): 152-157. ZHANG Ning, ZHOU Tianrui, DUAN Changgang, et al. Impact of large-scale wind farm connecting with power grid on peak load regulation demand[J]. Power System Technology, 2010, 34(1): 152-157.

[8]孔飞飞, 晁勤, 袁铁江, 等. 用于短期电网调度的风电场储能容量估算法[J]. 电力自动化设备, 2012, 32(7): 21-24. KONG Feifei, CHAO Qin, YUAN Tiejiang, et al. Estimation of wind farm energy storage capacity for short-term power dispatch[J]. Electric Power Automation Equipment, 2012, 32(7): 21-24.

[9]丁明, 徐宁舟, 毕锐. 用于平抑可再生能源功率波动的储能电站 建模及评价 [J]. 电力系统 自动化, 2011, 35(2): 66-71. DING Ming, XU Ningzhou, BI Rui. Modelling of BESS for smoothing renewable energy output fluctuations[J]. Automation of Electric Power Systems, 2011, 35(2): 66-71.

[10]张文亮, 丘明, 来小康. 储能技术在电力系统中的应用[J]. 电网技术, 2008, 32(7): 1-9. ZHANG Wenliang, QIU Ming, LAI Xiaokang. Application of energy storage technologies in power grids[J]. Power System Technology, 2008, 32(7): 1-9.

[11]于芃, 赵瑜, 周玮, 等. 基于混合储能系统的平抑风电波动功率方法的研究[J]. 电力系统保护与控制, 2011, 39(24): 35-40. YU Peng, ZHAO Yu, ZHOU Wei, et al. Research on the method based on hybrid energy storage system for balancing fluctuant wind power[J]. Power System Protection and Control, 2011, 39(24): 35-40.

[12]于芃, 周玮, 孙辉, 等. 用于风电功率平抑的混合储能系统及其控制系统设计[J]. 中国电机工程学报, 2011, 31(17): 127-133. YU Peng, ZHOU Wei, SUN Hui, et al. Hybrid energy storage system and control system design for wind power balancing[J]. Proceedings of the CSEE, 2011, 31(17): 127-133.

[13]韩晓娟, 陈跃燕, 张浩, 等. 基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J]. 中国电机工程学报, 2013, 33(19): 8-13, 24. HAN Xiaojuan, CHEN Yueyan, ZHANG Hao, et al. Application of hybrid energy storage technology based on wavelet packet decomposition in smoothing the fluctuation of wind power[J]. Proceedings of the CSEE, 2013, 33(19): 8-13, 24.

[14]张广韬. 利用储能装置平抑风电预测误差的可行性研究[D]. 北京: 北京交通大学, 2013. ZHANG Guangtao. The feasibility study of depressing wind power prediction error by energy storage device[D]. Beijing: Beijing Jiaotong University, 2013.

[15]阿丽努尔·阿木提, 晁勤, 罗建春. 提高风出力预测精度的储能系统模糊控制策略 [J]. 可再生能源 , 2014, 32(5): 624-629. ALINUER AMUTI, CHAO Qin, LUO Jianchun. Fuzzy control strategy for energy storage system to improve prediction accuracy of wind power output[J]. Renewable Energy Resources, 2014, 32(5): 624-629.

[16]胡续坤, 王筱, 晁勤. 提高风电功率短期预报精度的储能控制策略优化及效益评估[J]. 可再生能源, 2014, 32(12): 1821-1827. HU Xukun, WANG Xiao, CHAO Qin. Strategy optimization of energy storage control to increase short-term forecast accuracy of wind power and its performance evaluation[J]. Renewable Energy Resources, 2014, 32(12): 1821-1827.

[17]GBT_19963-2011 风电场接入电力系统技术规定[S].

[18]QBGDW432-2010 风电调度运行管理规范[S].

[19]娄素华, 吴耀武, 崔艳昭, 等. 电池储能平抑短期风电功率波动运行策略[J]. 电力系统自动化, 2014, 38(2): 17- 22, 58. LOU Suhua, WU Yaowu, CUI Yanzhao, et al. Operation strategy of battery energy storage system for smoothing short-term wind power fluctuation[J]. Automation of Electric Power Systems, 2014, 38(2): 17- 22, 58.

A control of BESS to improve the wind farm output based on time-varying intersection of dual targets

WANG Jingbiao1,2, LI Jiang3, HU Liqiang4, CHAO Qin1, RAO Chengcheng5, LI Zeran6, YIN Zhimin7, YANG Yang7, REN Juan8
(1. School of Electrical Engineering, Xinjiang University, Urumqi 830047, China; 2. State Grid Hengyang Power Supply Company, Hengyang 421001, China; 3. State Grid Changji Power Supply Company, Changji 831100, China; 4. Project Environmental Quality Supervision Station of Xinjiang Military Area, Urumqi 830002, China; 5. Maintenance Company of State Grid Hunan Electric Power Corporation, Changsha 410004, China; 6. State Grid Panjin Power Supply Company, Panjin 124010, China; 7. State Grid Huzhou Power Supply Company, Huzhou 313000, China; 8. State Grid Xinjiang Institute of Economic Technology, Urumqi 830000, China)

A battery energy storage system (BESS) control method based on time-varying intersection of the dual targets is proposed to suppress the random fluctuation of wind power and improve the accuracy of ultra short-term prediction of wind power. Firstly, a respective single control limit, intersection combined control limit and further time-varying intersection combined control limit once different time-scale of the dual control targets is considered are established. On this basis, combined with the operating constraints of the energy storage, the final control strategy of battery energy storage to improve the wind farm output is arrived at. Secondly, valuation and forecast accuracy assessment metrics based on off-limit probability and off-limit relative mean value is set up and comprehensive evaluation system of the dual targets is developed. Finally, by applying the real output data of a wind farm, on the premise of using neural network time series model or ARIMA model, three size relations of tolerance of wind fluctuation and tolerance of ultra short-term prediction error is considered to verify the effectiveness of the control strategy by calculating the total variation and RMSE and meanwhile both suppress random fluctuation and improve the ultra short-term prediction accuracy of wind power.

This work is supported by National Natural Science Foundation of China (No. 51267020).

time-varying intersection of dual targets; suppress fluctuation; ultra short-term prediction; BESS; off-limit probability and off-limit relative mean value

10.7667/PSPC151561

：2015-11-13

王境彪(1992-)，男，硕士研究生，研究方向为高校可靠风力发电技术。E-mail: yemai984872758@163.com

(编辑 周金梅)

国家自然科学基金资助(51267020)