菲涅耳公式的研究及数值模拟

李军依，王淑颖，李　进，丁永文

(辽宁师范大学,辽宁 大连　116029)

*通讯联系人

菲涅耳公式的研究及数值模拟

李军依，王淑颖，李进，丁永文*

(辽宁师范大学,辽宁 大连116029)

摘 要：菲涅耳公式阐述了光在两种不同透明介质的分界面上，发生反射和折射现象时，反射光、折射光的振幅变化规律。本文通过对菲涅尔公式的变形处理，得到了新的表达形式,并且应用Matlab软件进行了数值模拟，使菲涅耳公式的物理意义更清晰明了。

关键词：菲涅耳公式；公式变形；数值模拟

1菲涅耳公式的意义

(1)

(2)

(3)

(4)

其中公式(1)、(2)是指反射光垂直和水平振幅分量与入射光垂直和水平振幅分量的比值；(3)、(4)是折射光垂直和水平振幅分量与入射光垂直和水平振幅分量的比值。

图1　在两种不同透明介质分界面上发生的反射和折射现象

2公式的变形

(5)

(6)

同理可推导出(7)、(8)：

(7)

(8)

菲涅尔公式是相对于振幅而言的，实际上，光强才是可测物理量，而光强与振幅的平方成正比。令Rs、Rp分别表示s光和p光的光强反射率 ，Ts、Tp分别表示s光和p光的光强折射率， 则得到如下公式：

(9)

(10)

(11)

(12)

这就是光在介质交界面上反射和折射过程中， s光和p光的光强反射率及光强折射率，与入射角i1和两介质相对折射率n的关系，从而可以方便地进行数值模拟及实验验证。

3数值模拟

利用MATLAB软件对公式(9)(10)(11)(12)进行数值模拟。分为以下两种情况：

第一种情况是相对折射率 n为定值时 ，假设取n =1.5，研究光强反射率和光强折射率随入射角i1的变化情况，得到图象如图2、3。

图2　Ts随入射角的变化关系

图3　Rp与入射角的变化关系

Rs-i1

(13)

Rp-i1

(14)

Ts-i1

(15)

Tp-i1

(16)

由图(2-3)可以看出：

在入射角为57°左右时，水平方向的光强反射率Rp为0，Rs不为0，此时反射光为线偏振光，偏振方向与s方向平行，该入射角即为布鲁斯特角，图象较直观地验证了布鲁斯特定律。

当相对折射率n一定时，水平方向的光强反射率Rp以布鲁斯特角为转折点，先随入射角i1的增大缓慢减小直至为零，后Rp迅速增大。垂直方向的光强反射率Rs随入射角i1的增大而逐渐增大。

图4　Ts随入射角的变化关系

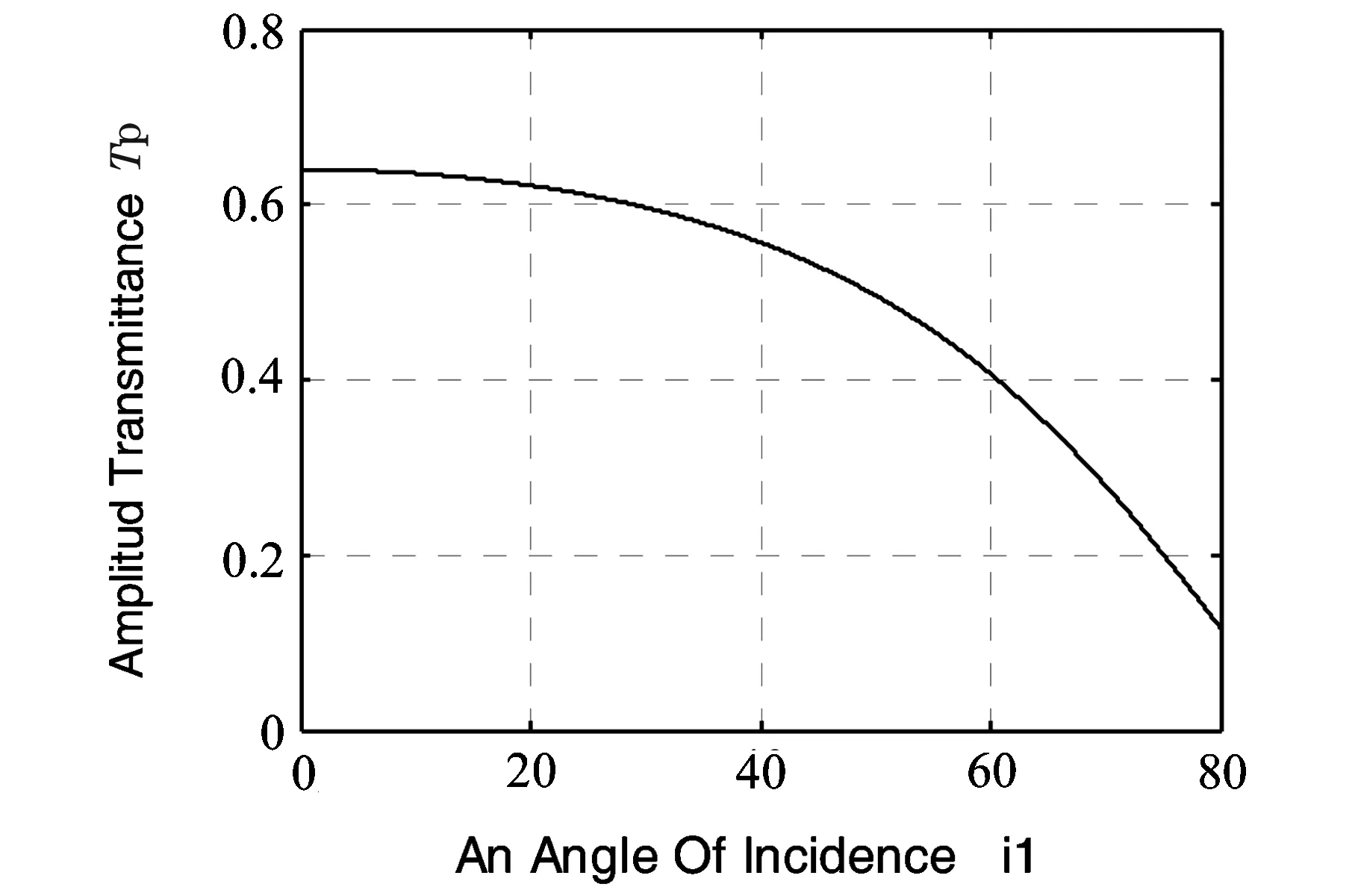
图5　Tp随入射角的变化关系

由图(4)、(5)可以看出：

当相对折射率n一定时，水平方向的光强折射率Ts 、垂直方向的光强折射率Tp都随入射角i1的增大而逐渐减小的。

图6　Rs随n变化关系

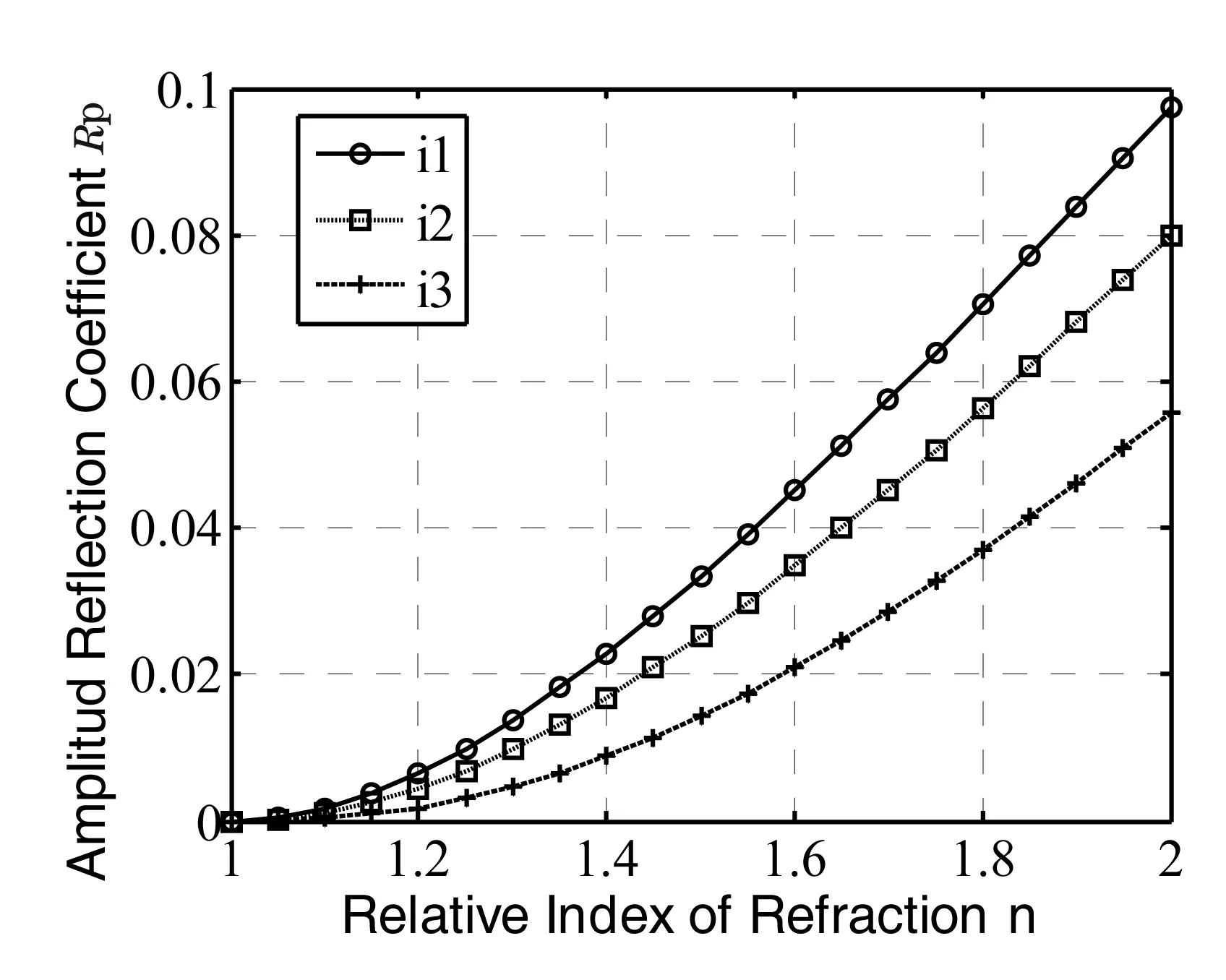
图7　Rp随n的变化情况

第二种情况是入射角i1为定值时，研究光强反射率和光强折射率随介质相对折射率n的变化而变化的情况。分别以入射角为i1=20°、i2=30°、i3=40°为例进行模拟，得到图象如图6-9。

图8　Ts随n变化情况

图9　Tp随n变化情况

Rs-n(i1、i2、i3)

(17)

Rp-n(i1、i2、i3)

(18)

Ts-n(i1、i2、i3)

(19)

Tp-n(i1、i2、i3)

(20)

图像表明：光强反射率Rs、Rp随相对折射率n的增大而增大,光强折射率Ts、Tp随相对折射率n的增大而减小。

参考文献：

[1]姚启钧.光学教程(第三版) [M].北京:高等教育出版社,2002.

[2]陈思音,田丹,何芳君,等.光的界面反射特性研究[J].大学物理实验,2015,28(3):2-4.

[2]尹中文， 轩爱华.光学薄膜反射率的计算[J].南阳师范学院学报,2007,6(3)：1.

[3]曹鸿,宋连科,偏振光入射方位角与介质反射率关系研究[J].曲阜师范大学学报,2004,30(2)：1-2.

[4]崔明,江成,崔元顺.材料磁性对电磁理论中菲涅尔公式的影响[J].电气电子教学学报,2014,36(4)：1-3.

[5]田秀芳.光波在左手材料中的菲涅尔公式和布儒斯特定律[J].光子学报,2006,35(7)：2-3.

[6]刘璐，谷开慧，孙晓冰，等.耦合映像格子模型时空混沌的控制[J].大学物理实验，2015(6)：11-13.

Experimental Study and Numerical Simulation of Fresnel Formula

LI Jun-yi,WANG Shu-ying,LI Jin,DING Yong-wen

(Liaoning Normal University,Liaoning Dalian 116029)

Abstract：Fresnel formula presents the law for the change of amplitude when reflection or refraction of light happens on two different kinds of transparent media.By deformation treatment of Fresnel formula,the paper gained a new expression and generated numerical modelling through applying Matlab,which makes it clearer and simpler of Fresnel formula’s physical significance.

Key words：Fresnel formula；the formula of deformation；numerical simulation

收稿日期：2015-11-22

基金项目：辽宁省大学生创新创业系列计划项目(201310165014)

文章编号：1007-2934(2016)02-0034-04

中图分类号：O 4-39

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.002.009