用波尔共振仪研究混沌现象

李百宏，强　蕊

(西安科技大学,陕西 西安　710054)

用波尔共振仪研究混沌现象

李百宏，强蕊

(西安科技大学,陕西 西安710054)

摘 要：用半导体激光器作为光源，用鼠标作为位移传感器，将波尔共振仪摆轮的振动转化为鼠标的运动轨迹，并通过Ghost Mouse-Setup软件记录鼠标轨迹，最后通过Labview软件对记录的轨迹进行信号处理，通过观察分析吸引子来研究波尔共振仪中的混沌现象。实验结果表明：波尔共振仪中摆轮做阻尼振动时，其振动振幅出现随时间逐渐减小，最终停止摆动的确定性规律，但每一次摆轮的运动过程都是随机的，各不相同。只要时间足够长，摆轮最终都会收缩成一点，形成稳定的焦点，即混沌吸引子。这就是波尔共振仪中摆轮做阻尼振动出现的混沌现象。

关键词：波尔共振仪；混沌现象；鼠标；Labview

波尔共振仪是目前大学物理实验教学中最常使用的对简谐振动、阻尼振动和受迫振动等多种物理实验现象进行观察和测量的实验装置[1,2]。同时，用它还可以进一步观察和研究混沌现象[3-7]。本实验利用本校物理实验室现有的实验仪器，采用半导体激光器作为光源，用鼠标作为位移传感器，将波尔共振仪摆轮的振动转化为鼠标的运动轨迹，并通过Ghost Mouse-Setup软件记录鼠标轨迹，最后通过Labview软件对记录的轨迹进行信号处理，通过观察分析吸引子来研究波尔共振仪中的混沌现象。

1实验原理

动力系统长时间演化的极限状态，即在t→∞时系统状态的归宿，称为吸引子。只有耗散系统才有吸引子。而波尔共振仪由于存在较小的阻力，同时可以人为地加上一定的阻力，使耗散放大化，便于观察。在二维系统中，吸引子主要是稳定的结点，焦点和极限环3种。波尔共振仪的结构如图1所示：

众所周知，光电鼠标是电脑的一个部件，其内部有一个光学感应器，是鼠标的核心，其实质相当于一个位移传感器，在日常生活中，当移动鼠标时，屏幕上的光标便随之移动，同样，如果保持鼠标不动，移动鼠标垫，光标依然跟着移动。在本实验中，通过铁架台将鼠标固定在摆轮的一侧，而摆轮则充当“鼠标垫”。实验时，当摆轮振动时，光标便移动，从而实现了对摆轮振动信号的非接触性连续测量[5]，由于光电鼠标内部的发光二级管光太弱，以至于必须使鼠标与摆轮足够近才可以，为此，采用半导体激光器来增强鼠标对光的敏感性。

波尔共振仪可以用来做近似自由振动、阻尼振动等试验，而波尔共振仪存在内在的阻力(非线性)，使得振动具有不确定性，通过实验研究不确定性中的现象，进而作分析讨论。

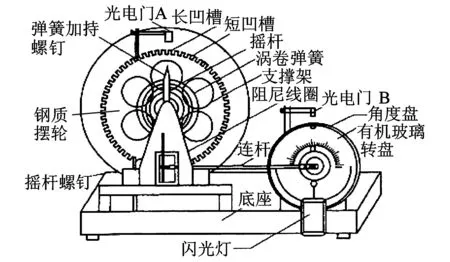
图1　波尔共振仪结构图

1.1摆轮的自由振动

摆轮的自由振动理论相图是一个闭合的圆，由于弹簧片存在较小的阻尼，所以摆轮的自由振动并非真正意义上的自由振动，它相当于外加一个较小的阻尼力矩做功，转化为热能耗散掉，它的轨迹会缓慢的趋向于圆心。

1.2摆轮的阻尼振动

在有阻力矩的情况下，使摆轮由某一摆角开始做自由振动，此时，摆轮受到两个力矩的作用：一是弹性恢复力矩，它与摆轮的扭转角成正比；二是阻力矩，可近似认为它与摆轮的角速度成正比。若摆轮的转动惯量为J，根据转动定律得摆轮的转动方程：

(1)

解得：

θ=A0e-βtcoswt

(2)摆轮的振幅θ随时间的指数规律衰减，通过数据采集不同时期下的θ值，可得由于内在阻力做功，转化为热能散失，故其运动轨迹将趋于一点，此点好像是吸引着其它点向它靠近，故称为奇异吸引子，通过测不同阻尼系数下的θ，作图对比得到一定的结论。

2实验流程

首先，按照实验原理连接实验装置，见图2。在连接实验仪器时，尤其是要注意鼠标与半导体激光器和波尔共振仪的相对位置，实验时，由于摆轮自身因素的影响，同时为避免鼠标自身反射光的接收，可以保持波尔共振仪和半导体激光器的位置不变，反复调节鼠标的位置，使得屏幕上的光标能够很好地刻画摆轮的振动状态。

手动调节有机玻璃盘上的零度标志线，使其指向0，此时的摆轮应静止于平衡位置，观察光电门A、B的位置，确保其通光且不与其他物接触。

2.1摆轮的自由振动

摆轮在适当角度(角度过大时，光标移出屏幕)做“自由振动”，将阻尼选择“0”档， 手动调节摆轮，使摆轮做自由振动，同时启动GhostMouse-Setup记录鼠标的运动轨迹，重复记录3次，选择最佳的一次。

2.2摆轮的阻尼振动

(1)将阻尼开关拨至“1”档，手动调节摆轮，使摆轮振动并记录其运动轨迹；

(2)将阻尼开关拨至“3”档，手动调节摆轮，使摆轮振动并记录其运动轨迹；

重复(1)(2)各3次。

图2　实验装置实物图

3实验结果与讨论

理论上，摆轮的自由振动应该是来回往复运动，由自由振动的波形图3可看到，由于存在较小的阻尼，系统将振动的能量转化为热能耗散掉，反映到图像上就是经过很长一段时间，摆轮趋于稳定的一点，此点就是系统的焦点，也称吸引子。

图3　(a)自由振动原始轨迹 (b)自由振动波形图表

由图4与图5对比可得，阻尼3档下，波形图表来回的次数少于阻尼1档下的波形图，说明了随着阻尼的增大，幅值衰减的越来越快，系统越容易趋向于稳定的焦点。综上，由于存在较小的内在阻尼，波尔共振仪的自由振动并不是真正意义上的自由振动，而阻尼振动由于人为地加了一定的阻力，使得系统的幅值衰减放大化，同时也时系统更容易向焦点靠近。

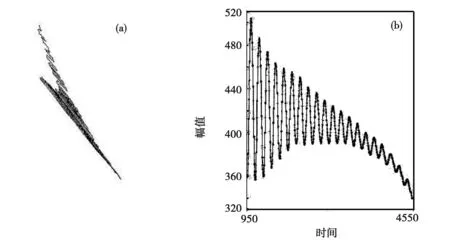
图4　(a)阻尼1下的原始轨迹 (b)阻尼1下的波形图表

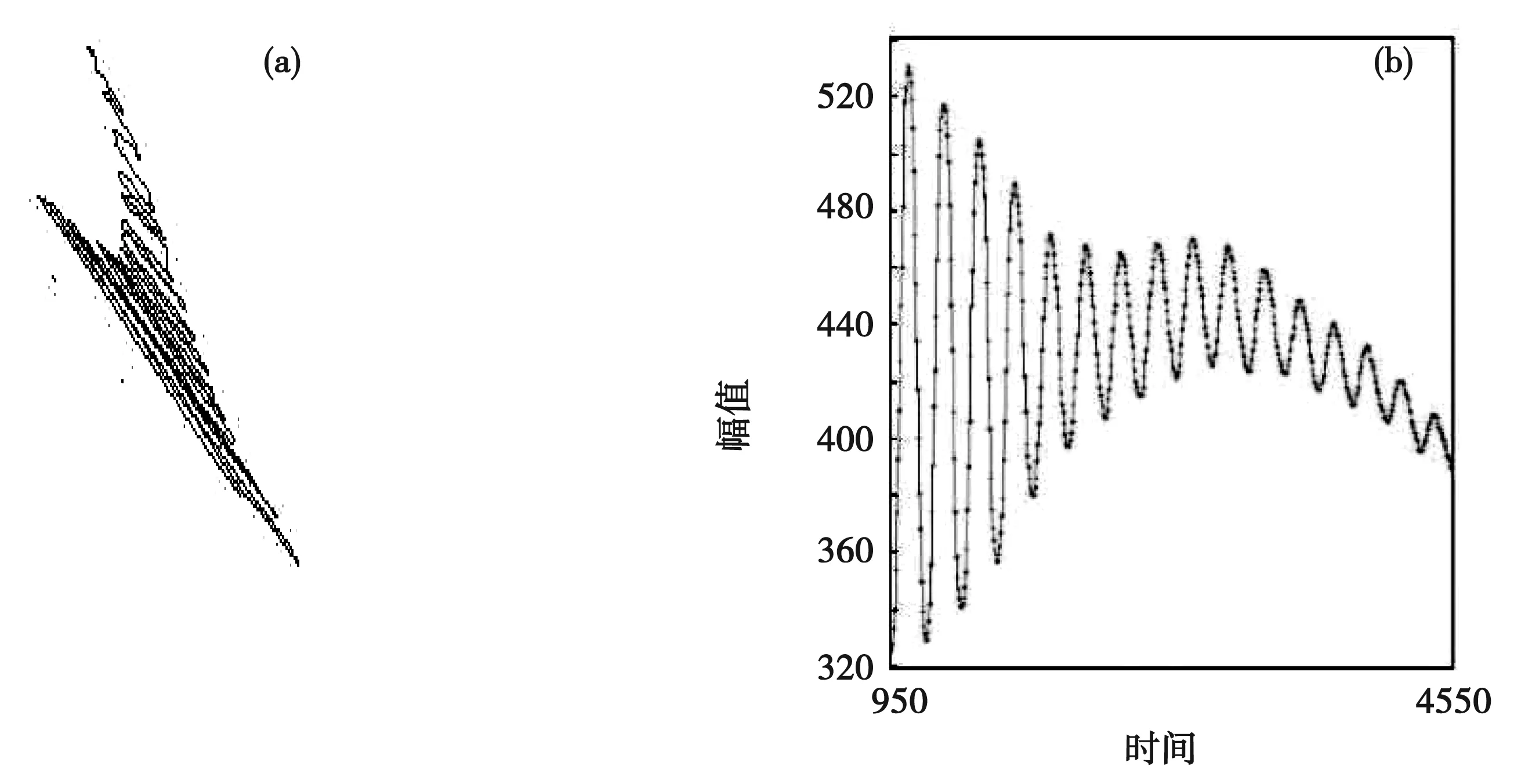
图5　(a)阻尼3下的原始轨迹 (b)阻尼3下的波形图表

由以上波形图可看出，幅值随时间的变化出现了向下的偏移，其原因可能是以下几点：

1)鼠标与摆轮的相对位置所影响。实验时，通过反复调节鼠标的位置，可能是鼠标的位置不是最佳位置，使得振动轨迹出现偏移量，在实验时，稍微改变鼠标的位置，轨迹都会有很大的变化；

2)实验时，由于鼠标自身的反射光被接受，改变了振动轨迹；

3)系统误差：摆轮本身并不是一个标准的质量分布均匀的物体，实际上是一个偏心轮；这将导致奇异吸引子的位置发生移动。

4结论

本文利用本校现有实验条件，对波尔共振仪中摆轮做阻尼振动出现的混沌现象进行了实验研究。结果表明，波尔共振仪中摆轮做阻尼振动时，其振动振幅随时间逐渐减小，最终停止摆动。这种振动的规律是确定的，只要有阻尼，波尔共振仪中摆轮的运动就属于耗散系统，系统最终必然趋向于稳定状态，只不过阻尼系数不同，达到稳定所需时间不同而已(阻尼系数越大，达到稳定所需时间越小)。在同一阻尼系数下，多次重复实验时，每一次摆轮的运动过程都是随机的，各不相同，但只要时间足够长，摆轮最终都会收缩成一点，形成稳定的焦点，即混沌吸引子。这就是波尔共振仪中摆轮做阻尼振动出现的混沌现象。我们通过实验室现有条件，认识和研究了波尔共振仪中出现的这种混沌现象，丰富了实验内容，扩展了我们的视野，对混沌现象及其规律有了一定的认识。

参考文献：

[1]解忧.新编大学物理实验[M].中国矿业大学出版社,2015.

[2]尤秉信,孙萍,翁俊荣.非线性实验的哲学意义[J].大学物理实验,2010(6)：38-43.

[3]郝柏林.分叉、混沌、奇怪吸引子、湍流及其他——关于确定论系统中的内在随机性[J].物理学进展,1983(3)：392-396.

[4]储琪,田玉龙,蒋达娅.利用光电鼠标实现玻尔共振仪混沌现象的数据采集[J].物理实验,2006(10):46-48.

[5]张海天,尹明,钟旋,等.改装鼠标器作为数据采集装置的方法及其应用[J].物理实验,2005(11)：42-44.

[6]赵斌，张宇亭，王茂香.弛豫对光磁共振实验的影响[J].大学物理实验，2015(2)：18-23.

[7]李雪梅，王玉华.Matlab软件和逐差法在共振法和相位法测量超声声速的应用[J].大学物理实验，2015(3)：91-93.

Research on Chaos Phenomenon Using Bohr Resonance Instrument

LI Bai-hong,QIANG Rui

(Xi'an University of Science and Technology,Shanxi Xi'an 710054)

Abstract：Using a semiconductor laser as a light source,a mouse as a displacement sensor,the vibration of balance wheel in Bohr resonance instrument is converted to the trajectory of the mouse which is recorded by the software of Ghost Mouse-Setup and processed by the software of Labview.The experimental results show that the vibration amplitude of balance wheel decreases gradually with time and stop finally in all damping vibrations,but the single vibration process of balance wheel is different and random.The vibration of balance wheel will eventually shrink to a point after enough time,to form a stable focus,namely chaotic attractor.This is chaos phenomenon of balance wheel damping vibration occurs in Bohr resonance instrument.

Key words：Bohr resonance instrument；chaos phenomenon；mouse；Labview

收稿日期：2015-10-29

基金项目：国家自然科学基金(No.11504292)

文章编号：1007-2934(2016)02-0017-04

中图分类号：O 322

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.002.005