非水平直圆管中黏性流体层流流量公式的推导及实验验证

路　阳

(北京农学院,北京 昌平　102206)

非水平直圆管中黏性流体层流流量公式的推导及实验验证

路阳

(北京农学院,北京 昌平102206)

摘 要：通过牛顿粘滞定律和修正后的伯努利方程对非水平直圆管中黏性流体作层流运动时的流量公式进行了推导。指出将泊肃叶公式中的压强视作广义压强，则文中的推导公式与泊肃叶公式完全一致。说明泊肃叶公式可以用来求解非水平直圆管中黏性流体作层流运动时的流量。本文通过实验验证了推导公式。

关键词：粘性流体；层流；流量公式推导；实验验证

在大学物理学中，流体力学部分的重点内容之一是关于不可压缩的粘性流体作层流运动时的流量的讨论，一些教材[1-6]以水平直圆管中粘性流体作层流运动时为例推导了流量公式，即泊肃叶公式。但并未说明非水平直圆管中的流量如何计算。

查阅文献发现有些文献[7-10]强调泊肃叶公式只适用于水平直圆管的粘性流体的流量计算；但有的文献[11]认为泊肃叶公式既适用于水平直圆管也适用于非水平直圆管。

本文通过牛顿粘滞定律和修正后的伯努利方程对非水平直圆管中黏性流体作层流运动时的流量公式进行了推导，并用实验验证了推导公式。

1非水平直圆管中黏性流体层流流量公式的推导

图1是半径为R的直圆管，其轴线与水平面成任意角。管中有不可压缩的粘性流体作层流运动。在管中选取与管同轴的半径为r，厚度为dr的单位长度的圆管状流体元，对该流体元流动中的能量进行分析。根据修正的伯努力方程[12]，流体元中单位体积的流体在始末位置处的总能量有如下关系

(1)

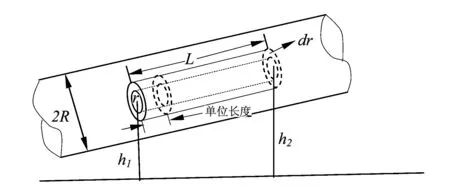
图1　直圆管流体层流分析图

(1)式中角标1，2分别表示流体元的初始位置和末位置，P代表流体压强，ρ表示流体密度，v是流动速度，h是流体元相对重力势能零势能面的高度，w是单位体积的流体流动中损耗的能量，g为重力加速度。当管中流体作定常流动，且流管各处粗细均匀，根据流体连续性原理，有v1=v2。(1)式可整理为

w=(P1-P2)+ρg(h1-h2)=(P1+ρgh1)-(P2+ρgh2)

(2)

由(2)式可知，图1中的研究对象“单位长度的流体元”在始末位置间损耗的总能量为

E=w2rdr

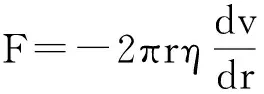
(3)

上式中η表示流体粘度。根据功能原理，流体元在流动中损耗的总能量等于其流动中受到的摩擦力做的总功。于是有

E=W

(4)

考虑到r=0时上式也成立，故c=0。得到

(5)

(5)式是直圆管中半径为r的流层的流动速度，由此式可以得出半径为R，长度为L的直圆管中粘性流体作层流运动时的流量Q为

(6)

将(2)式代入(6)式，得到

(7)

将(7)式中(P+ρgh)视为广义压强[10]，即流体压强与单位体积流体的重力势能之和，用符号P′表示广义压强，(7)式可改写为

(8)

(8)式给出了与水平方向成任何角度的直圆管中不可压缩粘性流体作层流时的流量计算公式，式中的压强为广义压强。(8)式与教材中的泊肃叶公式形式是一致的，只是公式中的压强含义有所不同。教材中泊肃叶公式中的压强为单纯的流动中的压强，而推导出的公式(8)中的压强为广义压强。当直圆管水平放置时，流体运动过程中重力势能不变，(8)式中的广义压强P’就等于流动中的压强P，此时(8)式与教材中的泊肃叶公式完全一致。

由上述推导可知，只要将泊肃叶定律中的压强视为广义压强，则泊肃叶公式既可用于水平状态直圆管的流量计算也可用于非水平状态的直圆管的流量计算。

2非水平直圆管中粘性流体层流流量公式的实验验证

本实验中以室温下的自来水作为粘性流体。图2是实验的装置简图。装置主要由两部分组成，①是恒水位槽，它由透明容器、进水管和溢水管组成；②是内半径R为1 mm，长度L为50 cm的细管。管的一端与恒水位槽连接，另一端对准一容器，管中水流质量可通过称量容器中承接的水的质量来确定。恒水位槽下方共安装了长度相同、内径相同的6根细管(图中未将其全部画出)，它们分别被固定在一竖直平面的不同位置上，与水平面方向分别成90°、75°、60°、45°、30°和15°。

保持恒水位槽中的水位高度H不变，分别采集1 min内与水平面成不同倾角的细管中的水流，称其质量，得到表1中的数据。

2.1细管中流体运动状态的确定

利用表1中与水平方向成90°角的实验数据，计算该细管中水流状态的雷诺数。该细管中1 min内水流平均质量为118.94 g，则1 s内水的体积流量为

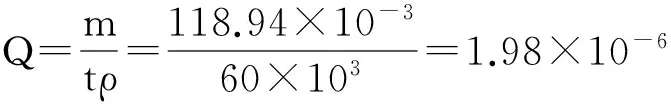
由上述讨论可知，与水平方向成小于90°的其它细管中的水的流动状态也一定为层流。说明我们的实验是在粘性流体作层流运动下进行的。

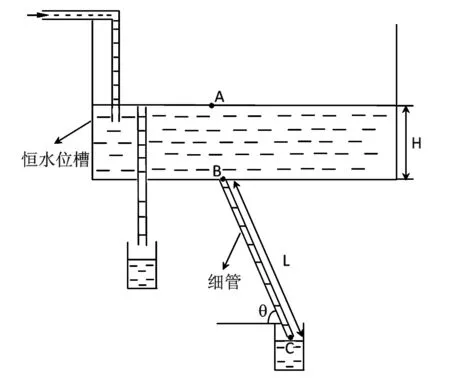
图2　实验装置简图

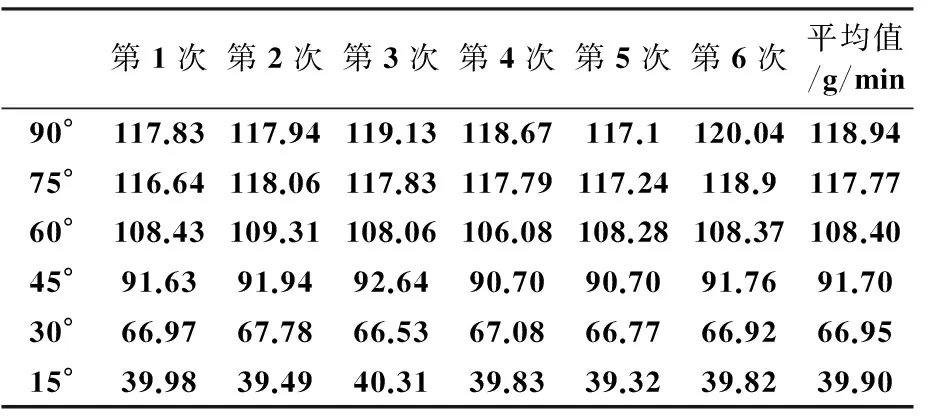
表1　与水平方向成不同角度θ的细管中

2.2流量与细管倾角关系的实验验证

本实验装置中，恒水位槽的横截面积远大于细管的横截面积，所以图2中细管两端的广义压强之差可表示为

ΔP′=ρgH+ρgLsinθ

(9)

上式中L为细管长度，θ为细管与水平面夹角。又因为细管长度远大于细管内径，细管中水流状态为层流，所以细管中的流量可以用推导出的公式(8)求解。根据(8)式，1 min内细管中的水流质量可表达为

(10)

(10)式中t为时间。

根据(10)式，若保持ρ、t、R、η、L、H不变，则水流质量m与sinθ应成线性关系。

根据表1中的实验数据，做出水流质量m与细管倾角正弦sinθ的关系图，如图3所示。

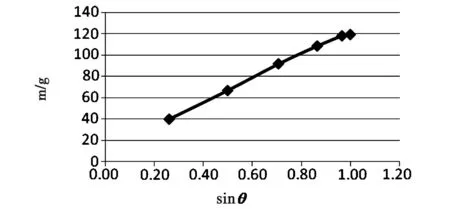
图3　细管倾角与水流质量关系图

从图3中可以看到，当sinθ较小时，m与sinθ能保持较好的线性关系，这与推导公式(10)相符。但是，当θ大于60°以后，m与sinθ偏离了线性关系。这是因为将图2中细管两端的广义压强之差表达为(9)式时，忽略了恒水位槽中水流运动时的损耗功及运动中的动能。

设图2中C点为重力势能零点，对图2中A、B两点列修正的伯努力方程

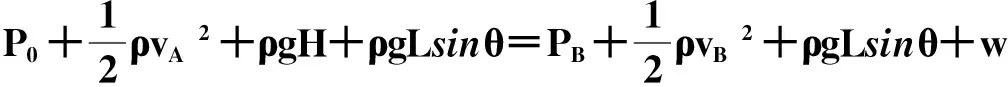
(11)

则B、C两点的广义压强之差为

(12)

(12)式中动能项和损耗功w是随流动速度的增大而增大的，因此它们是H和θ的正相关函数。当H保持不变时，若θ较小，此两项的和也较小，可以将其忽略不计，(12)式化为(9)式，水流质量m与细管倾角正弦sinθ成线性关系，如(10)式所示；当θ增大时，此两项的和增大到不能被忽略，将(12)式代入公式(8)，有

(13)

(13)式可以解释在图3中θ增大后m与sinθ失去线性关系的原因。

上述讨论说明，如果精确测量了流管两端的广义压强差，我们推导出的公式(8)与实验结果是相符的。

2.3流量与水位高度H关系的实验验证

以倾角为15°的细管为实验对象，在保持管内流动为层流的前提下，改变恒水位槽中的水位高度值，选取7个不同的H，采集1 min内细管的水流质量，实验数据见表2。根据表2的实验数据得到水流质量m和水位高度H的关系图，见图4。

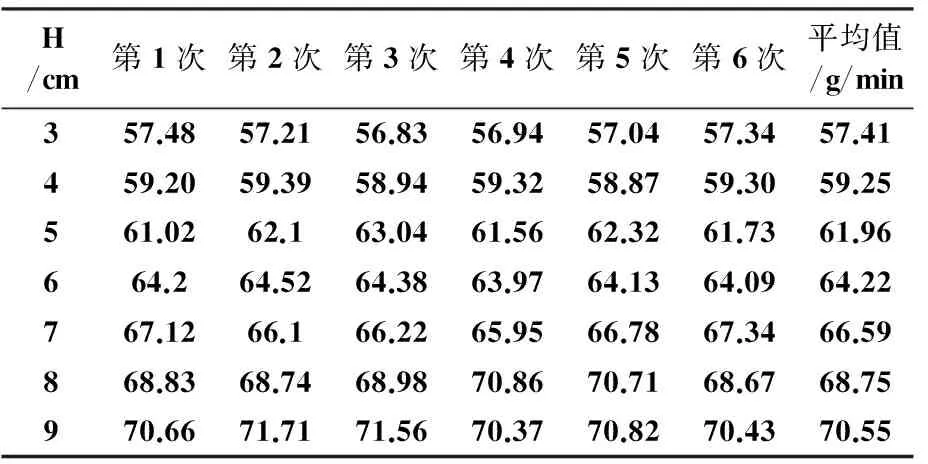
表2　不同水位高度时15°倾角细管中

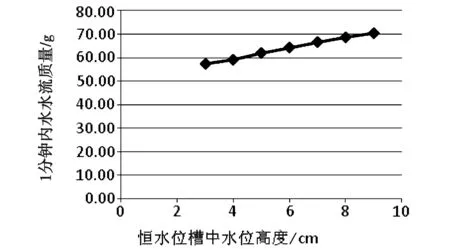
图4　水位高度与水流质量关系图

由图4可以看到，水流质量m和水位高度H成很好的线性关系。这是因为在15°倾角的细管中,对于不同数值的水位高度H，管中的流动速度都比较小，所以恒水位槽中水流运动时的损耗功及动能项对流量的影响可以忽略不计。

由实验求得的水流质量m和水位高度H的关系再次证明我们的推导公式是正确的。

3结论

本文通过牛顿粘滞定律和修正后的伯努利方程对非水平直圆管中黏性流体作层流运动时的流量公式进行了推导。将导出公式中的流体压强和单位体积流体的重力势能两项合在一起称为广义压强，则本文的导出公式与泊肃叶公式形式完全一致。说明将泊肃叶公式中的压强视作广义压强，该公式也适用于非水平状态的直圆管中黏性流体的流量问题。

本文对非水平直圆管中黏性流体作层流运动进行了实验研究，实验结果与推导公式相符。

参考文献：

[1]梁路光，赵大源.医用物理学 [M].北京：高等教育出版社，2004：47-48.

[2]喀蔚波.医用物理学(第二版)[M].北京：高等教育出版社，2008：51-52.

[3]胡玉才，李玉侠.大学物理学基本原理及生物效应 [M].北京：中国农业出版社，2004：29-30.

[4]周静娴.物理学 [M].北京：中国农业出版社，2002：10.

[5]金仲辉，申兵辉.大学物理简明教程 [M].北京：中国农业大学出版社，2007：15-16.

[6]金仲辉，柴丽娜.大学基础物理学 [M].北京：科学出版社，2010：57-58.

[7]黄慰怀.泊肃叶公式的适用条件 [J].中国大学教育，1992(1).

[8]阮萍.对泊肃叶定律应用的讨论 [J].华夏医学，1999(3)：268-269.

[9]黄秋萍.落球法液体粘滞系数实验的改进[J].大学物理实验，2015(3)：38-41.

[10] 吴晓，许建梅.液体粘滞系数实验实际问题的探讨[J].大学物理实验，2014(2)：75-77.

[11] 潘百年.物理学(供药学专业用)[M].北京：中国医药科技出版社，2000：13-14.

[12] 周光炯，严宗毅，许世雄，章克本.流体力学(第二版)下册 [M].北京：高等教育出版社，2000：54-55.

The Derivation of Viscous Fluid Flow Formula and Experimental Verification in Non-Horizontal Straight Round Tube

LU Yang

(Beijing University of Agriculture,Beijing 102206)

Abstract：According to the Newton’s law of viscosity and modified Bernouli equation,a flow formula of laminar flow of viscous fluid in non-horizontal straight round tube is derivate.When the pressure in Poiseuille formula is regarded as generalized pressure,the derivation formula is just Poiseuille formula.The derivation formula is proved by experiments.

Key words：viscous fluid；flow formula；derivation；experimental verification

收稿日期：2015-11-07

文章编号：1007-2934(2016)02-0030-04

中图分类号：O 4-34

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.002.008