如何提高学生解答复合应用题能力的培养

广西靖西市武平镇武平中心小学 赵桂芳

复合应用题是由两个或两个以上有联系的简单应用题组合而成的，需要通过两步或两步以上的运算才能解答。同时，复合应用题的已知条件多，结构比较复杂，多种的数量关系交织在一起，每次选用那两个已知数量进行哪一种运算，往往需要经过比较复杂的分析推理。因此，解答复合应用题是课堂教学中使学生应用所学的数学知识解决实际问题的必要的训练手段，又是发展学生思维能力的一种有效途径。

一、解答复合应用题中，使学生正确地找到中间问题

如从改变简单应用题的条件过度到两步应用题，突出中间问题。

题①：学校买彩色粉笔15盒，买白粉笔90盒，一共买多少盒粉笔？

题②：学校买彩色粉笔15盒，买白粉笔的合数是彩色粉笔的6倍。一共买粉笔多少盒？

题①和题②的问题和第一个条件完全一样，只是第二个条件不同。通过比较，学生可以发现：题①的两个已知数是所求问题的直接条件，通过一步计算就可以求出，“一共有多少盒粉笔”这个问题中。题②种“买白粉笔多少盒？”题中没有直接给出，所以要先把这个隐蔽的中间 问题求出来再求出题中最后的问题呢。

通过这种形式的过度训练，学生在比较中弄清两步应用题与简单应用题的联系和区别，学生学会了找出两步应用题中间问题，就可以用类推的方法来学习三、四步同类应用题。这样由易到难，由简到繁的训练，能收到较好的学习效果。

二、解答复合应用题中，让学生掌握解题思路

在解答复合应用题中，让学生掌握解题思路，在教学中，着重帮助学生掌握分析法和综合法的解题思路。如三年级有4个班，四年级有3个班，三年级每班40人；四年级每班有385人，三四年级一共有多少人？教学生时，先用分析法分析题里的数量关系。教师边提问，边把分析过程逐步板书出来，帮助学生理解题中的数量关系：

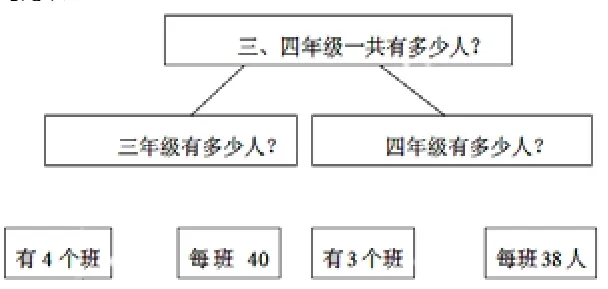
再用综合法分析，引导学生想，教师边提问边板书：

两种方法互相配合，协调运用，用分析法来分析题里的数量关系，寻求解题的途径，用综合法来列出算式。平时还通过问答，让学生复述分析的过程，逐步培养学生能够有根据地思考，比较完整地叙述思路，说明理由，还教学生利用图解进行分析，使解题思路有条有理地表述出来。

三、在解题中，让学生会列综合算式解答

在这方面，就要结合分布列式，逐层分析、对照，用代入法列出综合算式。

如例题：服装厂计划做660套衣服，已经做了5天，平均每天做75套，剩下的要三天做完，平均每天要做几套？可以引导学生把已知条件和问题用线段图表示出来，再表述分析思路，这样引导学生一步一步地列综合算式出分布算式。

另外，可以综合应用题里的数量关系的分析，教学生用填补法直接列出综合算式。如：

① 剩下的套数÷3

②（660－已做的套数）÷3

③（660－75×5）÷3

四、加强基本功训练，不断提高解答应用题能力

教学中，将几道容易混淆的应用题揭示出来，要求学生认真读题，独立分析数量关系，列出算式。还要求学生说出自己的思考过程，说明理由。进一步使学生熟悉数量关系，培养学生思维的灵活性和深刻性。

此外，用不同的方法解题，在比较中找出合理、简便的方法训练都不失题意，也是培养学生创造性思维的好方法。