复杂到简单 多样到统一——分数的起源、形成与发展

◇郁亚新

复杂到简单 多样到统一
——分数的起源、形成与发展

◇郁亚新

我们每天都在使用数，没有数也就没有今天的数学和其他科学。在所有的数中，对于分数大家都不陌生，分数是把单位“1”平均分成若干份，表示这样一份或几份的数。分数是怎样形成和发展的？分数又是谁发明的？

一 分数的起源

分数几乎和历史上最早产生的自然数一样古老。早在人类文化发展初期，由于在测量和均分时往往不能正好得到整数的结果，于是分数应运而生。

分数的产生经历了一个漫长的过程。在发明分数之前，人们使用画图的方法表示分数，比如：3个果子用 3个圆圈表示，那么1个果子平均分3份就先画1个圆圈，再平均分成3份。这样太麻烦了，于是古代人想出了新的方法来表示分数。

二 分数的形成

（一）各文明古国不同的分数表示形式。

1.分子总是1的分数——古埃及。

在埃及最重要的传世数学文献“莱茵德纸草书”中就记载了世界上最早的分数。很久以前，在埃及的尼罗河畔和沼泽地带，生长着一种像芦苇那样的水生植物。由于把这种水生植物的茎逐层剖开后可以用来写字，因此埃及人把它叫作“纸草”。莱茵德纸草书由英国研究埃及文化的学者亨利·莱茵德传播而得名，如图1。

图1

在纸草书上，古埃及人用一种特殊的记号来表示单位分数即分子为1的分数：在整数上方简单地画一个椭圆，就表示该整数的倒数，这样，可以用表示这种分数表示方式比画图简单多了。

有趣的是，埃及人对单位分数（即分子是1的分数）情有独钟。当遇到分子不为1的分数（例外，因为在埃及算数运算中扮演着特殊角色并用一个专门的记号来表示）时，埃及人的表示方式相当独特，他们想方设法把这样的分数转化为一些单位分数之和，如表示。这样，像这个分数，就必须用表示，以至这种分数表示方式使分数的计算非常烦琐。

从现代人的角度看，埃及分数的表示方式不是很理想甚至有点古怪。这种分数不但表示方式复杂，而且计算更为烦琐，这大概跟埃及人分东西的习惯有关。但它毕竟是目前已知人类发现最早的分数，让我们不得不佩服埃及人的智慧。

2.分母总是60的分数——古巴比伦。

古代巴比伦人（现处伊拉克一带）使用的是六十进制。因此，他们的分数也就使用60作为分母。公元前2100多年的巴比伦泥版文书记载了六十进制的分数，如用楔形文字表示这种六十进制的现象一直延续到现在，如1小时=60分，23分就可以用分数小时来表示。

3.算筹表示的分数——中国。

无论是分数的确切定义和科学表示，还是分数的一整套算法，最早把它们建立起来的是中国。我国古代有许多关于分数的记载。例如，春秋时期的《左传》中有“大都不过三国之一，中五之一，小九之一”的记载，意思是说各诸侯国的都城最大者不得超过周文王都城的中等的不能超过小的不能超过

在战国时齐国人所写的《考工记》中有“十分寸之一谓之枚”的记载（寸=1枚。“枚”字相当于后来的“分”字）。

在中国古代，分数是在用算筹做除法运算的基础上产生的。

图2 ：出土的汉代算筹

当除不尽时，把余数作为分子,除数作为分母，就产生了一个分子在上、分母在下的分数筹算形式。我国古算中用算筹表示分数有十分明确的规则，如今天的表示为：

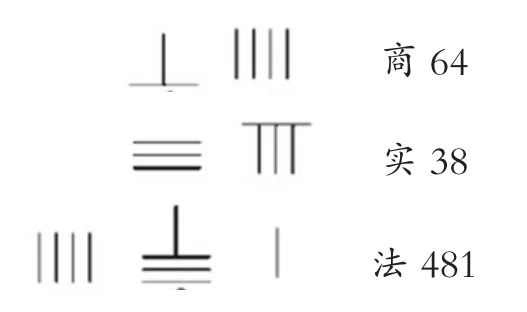
图3

又如：南宋数学家秦九韶的《数书九章》第九章卷一七“推求物价”一题独创了分数的另一种表示方法，即分子在上，分母在下。如图4表示

图4

这种表示方法跟现在分数中分子、分母的位置相同。

中国古人也把两个整数相除的商看作分数,在这种认识下，一个除法算式就表示一个分数，这种认识正是现在分数概念的基础。

（二）分数表示形式趋于统一。

1.分数的雏形。

印度人用六十进制记法表示天文上的分数，其他方面的分数他们用整数之比来表示。印度人记录的分数与中国古代的筹算分数是一样的，都把分子记在上面，分母记在下面，只不过他们使用的是阿拉伯数字，但中间没用横线隔开，例如分数的这种记法对世界的影响很大，多样的分数表示方式趋于统一并且越来越简单。

2.现在分数的形成。

（1）分数线的由来。

阿拉伯人采用并改进了印度的数字记号和进位记法。1175年，阿拉伯数学家阿尔·哈萨首先使用了“分数线”符号，用一条短线将分子、分母上下隔开，分数就成了今天这个样子。（“斜分数线”如7/3，是英国数学家德·摩根于1845年首先使用的）

13世纪初，意大利数学家斐波那契把阿拉伯人的这种分数记法介绍到了欧洲。

（2）“分数”名称的由来。

200多年前，瑞士数学家欧拉在《通用算术》一书中说：要想把7米长的一根绳子分成3等份是不可能的，因为找不到一个合适的数来表示它，如果把它分成 3等份，每份是米，是一种新的数，我们把它叫作“分数”。分数这个名称直观而生动地表示了这种数的特征。

三 分数的发展

分数刚刚形成时，人们心生畏惧，在拉丁文里“分数”一词的意思和打破、破裂相同，因此分数也曾被称为“破碎数”。在欧洲，这些“破碎数”曾令人谈虎色变，德国人形容某人陷入困境时，常引用一句古老的谚语，说“他掉到分数里去了”，他们视分数为畏途。

这是因为欧洲人采用罗马数字和单位分数，这种笨拙的分数表示形式及计算的烦琐，造成了人们对分数认识和应用的巨大障碍，所以西方分数理论发展得出奇缓慢，直到中世纪，随着印度—阿拉伯数字及其运算传入欧洲，西方惧怕分数的状况才有所改变。

而在中国，分数的发展却领先于世界其他各国。《九章算术》是我国的一本数学专著，其中第一章《方田》里就讲了分数四则运算，即约分、合分（分数加法）、减分（分数减法）、乘分（分数乘法）、除分（分数除法）的法则，与我们现在的分数运算法则完全相同。另外，其中还记载了课分（比较分数大小）、平分（求分数的平均值）等关于分数的知识，是世界上最早的系统阐述分数的著作。

从古到今，分数总以自己独特的形式展示自己的风姿，世界各地到处都有分数的身影。古希腊数学家丢番图的墓碑上就刻着一道分数题：

丢番图一生的六分之一是幸福的童年，十二分之一是无忧无虑的少年。

再过去七分之一的年程，他建立了幸福的家庭。

五年后儿子出生，不料儿子竟先其父四年而终，只活到父亲岁数的一半。

晚年丧子的老人真可怜，悲痛之中度过了风烛残年。

请你算一算，丢番图活到多大，才和死神见面？

这道别开生面的分数题不仅透露了丢番图的寿命，而且提供了他的一些生平资料。

分数经历了从复杂到简单、从多样到统一的过程，我们现代人看来很简单的分数，却是几千年来古今中外的学者历经艰辛创造的科学成果，闪烁着人类智慧的光芒。

[1]徐品方.数学趣史[M].北京:科学出版社，2013.

[2]朴海燕译.神奇的数字[M].石家庄:河北科学技术出版社，1995.

[3]徐炎章，王剑峰.敲开数学之门[M].北京：中国青年出版社，2013.

[4]李文林.数学史概论[M].北京：高等教育出版社，2011.

[5]郜舒竹.数学的观念、思想和方法[M].北京：首都师范大学出版社，2004.

（作者单位：江苏南通市虹桥小学）