基于思维导图的线性代数复习策略

陈晓艳

摘 要： 线性代数是硕士研究生入学考试《高等数学》科目的必考内容之一，概念抽象，性质，结论众多，考生在复习过程中不易把握，本文以思维导图为工具，从线性代数的核心概念——矩阵的可交换性入手，分析相关的考研试题，绘制出导图，得到本类问题的本质特征，进而指出思维导图对于学生形成自己的学习模块有辅助作用。

关键词： 思维导图 线性代数 可交换矩阵一、引言

思维导图（Mind Mapping）是英国Tony Buzan在20世记70年代初期所创的一种使人类更有效地利用大脑的笔记方法，是一种将放射性思考具体化的方法，它能帮助我们进行思考、理清思路。在我们不清楚问题、概念之间的关系时，从其中的一个问题或概念入手，利用思维导图可以把头脑中的信息联系起来，形成可视化的图表，从而使问题空间呈现可视化效果，以便深入了解这个问题，同时也加深对问题空间的认识[1][2]。

线性代数是硕士研究生入学考试高等数学科目的必考内容之一，在复习过程中，学生时常感到概念多、性质多，同时在做题的时候感到似曾相识却无从下笔。其实线性代数是一个整体的体系，如果我们在复习的时候有意识引入思维导图，就可以帮助我们把其中相关的模块联系起来，进而找到它们的关系，从整体上把握它们。

二、实例构建导图

下面我们就以矩阵中的一个小结论入手，看看思维导图能帮助我们获得什么。

我们从矩阵中的可交换矩阵入手，之所以选择它，是因为首先矩阵是线性代数里的一个核心概念，它和线性变换是不同形式下的同一事物，其次矩阵的乘积一般不满足交换律，但是当它满足交换律后，便带来了很多好的结论，因此是考研题型的热点之一。

我们收集了涉及可交换矩阵的考研试题，部分有代表性的如下：

（1）证明：设若n阶方阵A、B满足A+B=AB，则A、B可交换；（2）证明：若A，B为n阶方阵，满足AB=BA，则A，B有公共的特征向量；（3）证明：若A，B为n阶方阵，满足AB=BA，则存在n阶可逆阵T使得：

（4）若A，B为n阶可对角化方阵（也可说它们的初等因子皆为一次的），满足AB=BA，则存在n阶可逆阵T使得A，B可同时对角化。（5）若A，B为n阶实对称阵，则AB=BA的充要条件是存在n阶正交阵T使得A，B可同时对角化。

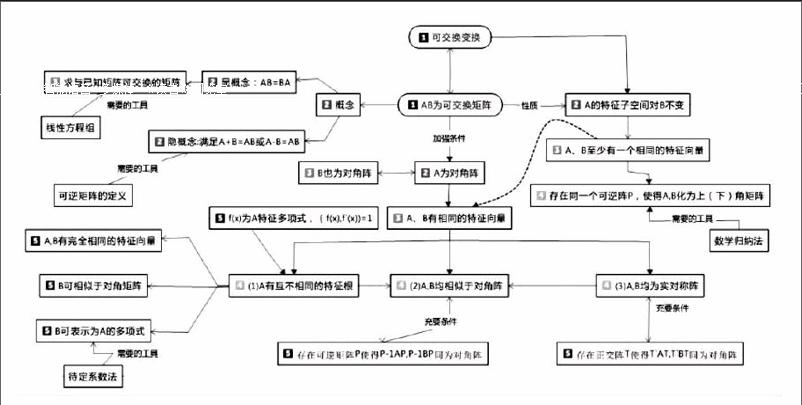
我们在分析以上各题的解题思路基础上，以mind manager为工具，最终绘制导图如下：

从下图可以看出：

1.作为第一优先级级的是可交换矩阵和可交换线性变换，也即我们这里列出的所有有关可交换矩阵的概念和结论，在可交换线性变换中同样适用。

2.作为第二级的有概念、性质

（1）概念

A，B可交换的概念有两个，第一个是显概念，也即一般的教科书上给的定义，我们遇到的题目（我们把它归到第三级）一般是已知一个低阶矩阵，要求可与它相交换的矩阵的集合，其中需要用到矩阵乘积、相等，解线性方程组等知识点。

第二个概念是一类考研题，我们把它称为可交换矩阵的隐概念，也即当满足A±B=AB时，有AB=BA。要证明这个结论，需要用到可逆矩阵的定义（即AB=BA=I）。一般来说，考研试题中会把它作为一个条件，加入到一个大题中，其本质是A，B满足可交换性。

（2）性质：当A，B满足可交换时，A，B中至少有一个相同的特征向量。

这是一个关键性质，需要用到特征子空间和不变子空间的概念，也即A的属于某个特征根的特征子空间V是B的不变子空间；

这个性质可得到好的结论：存在可逆矩阵P，使得均为上（下）三角阵。其证明思路是从的这个特征子空间的基入手，构建的基，利用数学归纳法可以证明。

3.考研热点

考研试题中经常出现的有关可交换矩阵的一类较难的试题是在第4级和第5级，但通过思维导图会发现，它们的条件、形式虽然不同，但均需要利用A，B有相同的特征向量这一条件，但性质中给出的是当A，B满足可交换时，A，B中至少有一个相同的特征向量，为了得到有完全相同的特征向量，需要加强条件：“A可对角化”。也即：

当AB=BA，并满足A可对角化时，B也可对角化，且A，B有相同的特征向量。这里需要用到的结论有：（1）当A为对角阵，且AB=BA时，B也为对角阵；（2） 存在可逆阵P，使P为对角阵。

（1）当有个互异的特征根时（有的考研题在这里也会设个套，即给出关于的特征多项式的根的特征： （f（λ），f′（λ）=1），显然A可对角化，其结论有三个：

①A，B有相同的特征向量（其作成的列向量组即为矩阵P）；

②B也可对角化；

③B可表示为的多项式形式。

结论1、2 是A可对角化的两个结论，第三个需要用到待定系数法，设出形式多项式，通过矩阵的相等，方程组的解结构，行列式的性质等证明。