高职数学教学多维化模式探索
李慧敏
(无锡卫生高等职业技术学校,江苏 无锡 214028)
高职数学教学多维化模式探索
李慧敏
(无锡卫生高等职业技术学校,江苏 无锡 214028)
摘要:高职教育发展相对滞后,长期得不到应有的重视,形成了割裂性、弱化性、静态性的特点,无法适应现代职业化发展的要求。根据职业能力属性和现代性要求,多维化高职数学教育是实现职业化取向的有效尝试,具体包括数学教学内容、方法、考核等多维度模式。
关键词:高职数学教学;多维模式;职业化取向
0引言
长期以来,我国高等教育重心过于偏重传统高等教育,适龄优秀毕业生多以考取高等学校为奋斗目标,尤其近些年来,高等教育的扩大化、本科化、同质化等特点更使得高校毕业生难以适应现代职业化取向,人才供给与人才需求错位,现代职业化教育需求迫切。与此同时,职业教育却长期得不到应有的重视,更使得职业教育难以集中更好的师资和生源,加上传统职业教育的单一化、任务化、操作化等简单教学,常常忽视数学等基础教育,使得高职毕业生无法在毕业时利用数学等基础能力,适应现代职业信息化、网络化、动态化等发展特点,无法带来职业能力的提升。本文根据职业能力属性和现代性要求,多维度探讨了高职数学教学的职业化取向。
1我国高职数学教学特点
1.1割裂性
近年来,随着我国对职业教育的逐步重视,高职教育基本引入了数学等基础学科的教学。但由于传统高职教育更注重对于专业操作能力的培养,数学等基础学科教育长期以来得不到应有重视,数学教学内容也仅是同级高中教育、大学教育等传统讲授式教学,内容无法与高职学生未来职业能力相衔接,这就造成了目前我国高职数学教育的割裂性。
1.2弱化性
我国职业院校学生的基础普遍较差,在学习能力、学习动力尤其学习数学能力上都有或大或小的差距,同时,由于一些高职学校刻意追求就业率,造成教育教学的短视化,只注重现有操作化、简单化的职业能力教学,忽视数学等基础教育,更加重了我国高职学生数学教育的弱化性。
1.3静态性
由于我国高职数学教育缺乏职业能力取向,缺乏对数学基本思想的教学,教学内容仅停留在高中和本科教学内容上,教育方法更是以传统讲授式为主,这就造成了我国高职数学教育的静态性,无法适应现代职业发展的网络化、信息化、快速化的普遍动态性要求。
2高职教育的现代职业能力需求
2.1职业能力定义
目前,职业能力还未有一个明确的定义,下表是世界各国对职业能力的主要论述。

国家关键能力内容英国交流能力,解决问题能力,计算能力,信息技术能力,语言运用能力。美国分配时间:制定目标和突出重点目标的能力,分配经费和预算能力,确定所需要的数据并处理和保存数据的能力,作为小组成员参与活动以及与操作能力,了解社会、组织和技术系统是如何运行以及操作的能力,选择技术的能力,在工作中应用技术的能力。德国与个人相关的能力:求知欲,自我革新,学习能力,耐挫能力,责任感,冒险精神,独立性等。社会和组织能力:沟通能力,使用能力,分析能力,计划能力,组织能力。澳大利亚收集、分析、处理意见和信息的能力,表达意见和交流信息的能力,规划和组织活动的能力,在团体中与他人合作共事的能力,运用数学思维和技巧的能力,解决问题的能力,利用新技术的能力。
2.2职业能力属性
职业能力的属性概括为:自然属性,社会属性,技能属性,心理属性。
自然属性,是职业能力客观存在的,即为什么需要特定的职业,特定职业可以实现哪些自然功能,可以解决和满足哪些客观需求。
社会属性,是指职业能力具有社会性,职业是在特定的组织中实现的社会功能,如果是个体职业者,也需要在特定的社会环境中,实现职业的功能。
技能属性,是指职业需要一定的技能才可以实现职业的基本功能,技能是职业者与自然、社会的相调适的结果。
心理属性,是指职业者是有生命、有活力的个体,因此需要发挥职业者的主观能动性,促成职业能力的不断发展。
2.3职业能力的现代性
通过对职业能力属性的研究可知,职业能力的基本属性都是在动态变化的,即自然是动态运动的,社会是不断发展的,技术是不断革新的,心理因素也是不断变化的,这就促成了职业能力不是静态的,而是动态的、相对的。
目前,世界范围内信息化、数字化、网络化已成为现代诸多职业的共同特征,
而信息化、数字化、网络化的实现方式是通过数学中自然逻辑的表达,因此数学促成了职业现代化特征,适应职业现代化要求离不开数学。
2.4高职数学教育是职业现代能力基础需求
高职教育的最终目标是培养职业化人才,而当今职业特征的信息化、数字化、网络化是对目前和未来的职业化人才的基本需求,缺少了数学的知识和能力,就很难适应未来职业化发展的要求,就会失去职业化不断发展进步的基础。
3高职数学教学方法职业化取向多维模式
高职数学教学方法职业化取向的核心,是改变高职数学现有教学模式的割裂性、弱化性、静态性特征,丰富教学内容,拓展教学方法,创新教学考核,根据职业能力属性,结合职业能力的现代性,形成高职数学教学的多维模式。
3.1多维度教学内容
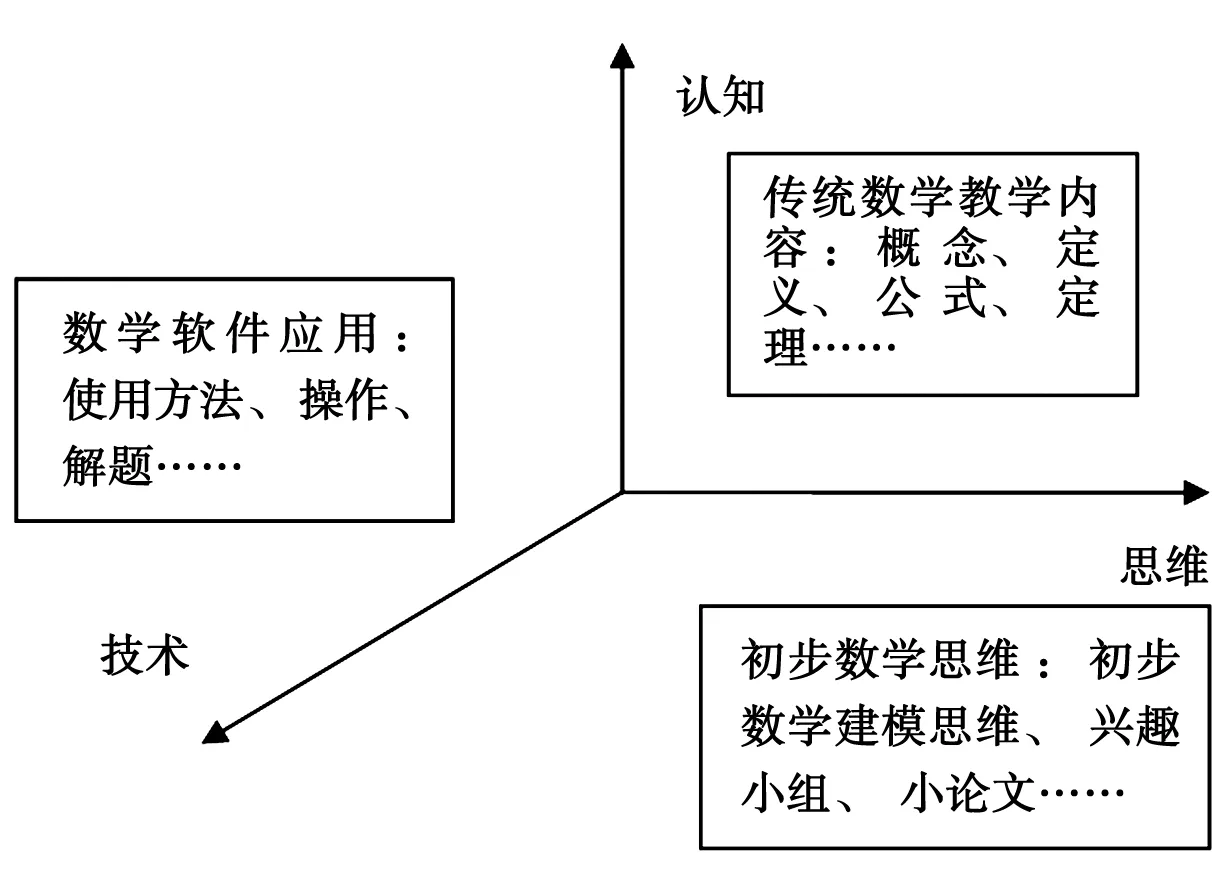
高职数学教学的职业化取向的基础是丰富教学内容,从而适应现代职业化的取向要求,但丰富教学内容不仅是对传统原有教学内容的简单挖掘,而是要结合现代职业化要求,形成多维度的教学内容。这里将教学内容维度概括为认识、技术、思维三个维度。
认知维度:主要教学内容是传统数学的概念、定义、公式、定理等。
技术维度:主要根据目前信息技术的发展,结合互联网和计算机技术等对数学软件进行应用。
思维维度:掌握最基础的数学建模思维,组成兴趣小组,结合职业方向,定期进行小论文研究。
3.2多维度教学方法
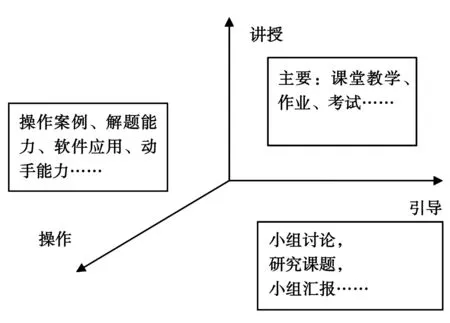
在丰富的多维教学内容的基础上,必须要有多维度数学方法才可以实现,才能将高职数学教学的职业化取向付诸实施。根据上述教学内容的基础维度,将数学教学方法也概括为三个基本维度:讲授、操作、引导。
讲授维度:主要采用传统的课堂教学、作业、考试等方法,但在实际操作过程中要不断丰富讲授艺术,激发学生的主动性,保证教学效率。
操作维度:结合不同专业的职业化要求,以计算机、互联网和数学软件等为对操作对象,强调操作案例、解题能力、软件应用、动手能力的教学。
引导维度:通过特定具体问题,引导学生进行小组讨论,深入引导进行课题研究,形成小论文和汇报材料,进行小组汇报等。
3.3多维度教学考核
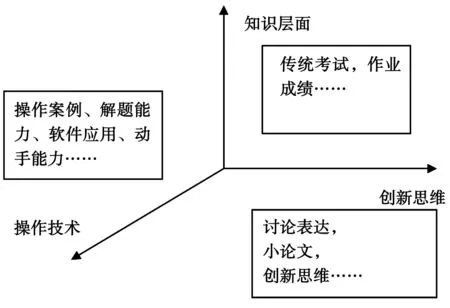
根据多维度的教学内容,实施多维度的教学方法,更要加强多维度的教学考核,因此必须实现多维度教学考核。考核维度可以概括为知识层面、操作技术、创新思维三个维度。
知识层面:传统的考试成绩和作业成绩;
操作技术:操作案例、解题能力、软件应用、动手能力等;
创新思维:讨论表达、小论文、创新思维等。
在实际考核过程中,可以根据学生特点、职业化的要求等将各层面的教学考核赋予科学的权重。
4结语
我国职业化数学教育常常受到忽视,职业化数学教育形成割裂性、弱化性、静态性特点。必须根据现代职业化要求,实现职业化数学教学取向多维模式,即多维度教学内容、多维度教学方法、多维度教学考核,进而满足高职数学教学的职业化取向。
参考文献:
[1]陈珠社.浅议高职数学教育中存在的问题与对策[J].中外企业家,2011(8).
[2]张雄. 数学教育学概论[M]. 西安:陕西科学技术出版社,2001.
[3]史炳星. 美国数学教育中的问题解决[J].北京教育学院学报,1998.
[4]Bransford, John D, Rodney R Cocking. How People Learn: Brain, Mind, Experience, and School.[M]Washington, DC: National Academy Press,1999.
[5]郑毓信. 数学教育的现代发展[M].南京: 江苏教育出版社,1999.
[6]郭炯. 职业能力研究的文献综述[J].高等职业教育(天津职业大学学报),2009(4).
(编辑马海超)
Exploration of Multidimensional Mode of Mathematics Teaching in Higher Vocational Colleges
LI Huimin
(Wuxi Higher Health Vocational Technology School, Wuxi 214028, China)
Abstract:Higher education’s development lags behind, not given due attention for a long time, which forms the fragmented, weakened resistance, and static characteristics, unable to adapt to the requirements of modern professional development. According to the professional competence property and modern requirements, multidimensional higher vocational mathematics education is an effective attempt to achieve professional orientation, including mathematics teaching contents, methods, assessment and other multidimensional models.
Keywords:higher vocational mathematics teaching; multidimensional mode; professional orientation
收稿日期:2016-02-13
作者简介:李慧敏 (1984—),女。安徽宣城人。助教,硕士研究生。研究方向:数学教育研究。
中图分类号:G712
文献标识码:A文章编码:1672-0601(2016)05-0060-03

