Poisson回归模型及Lasso变量选择在研究生成绩影响因素分析中的应用

艾冬梅，　黄若诚，　梁晓一，　宁晓钧

(1. 北京科技大学数理学院，北京100083；　2. 北京科技大学研究生院，北京100083)



Poisson回归模型及Lasso变量选择在研究生成绩影响因素分析中的应用

艾冬梅1，黄若诚1，梁晓一1，宁晓钧2

(1. 北京科技大学数理学院，北京100083；2. 北京科技大学研究生院，北京100083)

[摘要]探究学生成绩的主要影响因素是研究学生成绩评价体系中一个重要方向.依据某大学三年研究生入学信息数据，利用方差分析研究其入学成绩的影响因素；利用Poisson回归模型结合Lasso变量选择方法，探究入学专业课成绩、培养类别等对研究生学业课程成绩是否有显著影响，其结果为研究生院的招生工作提供了数据支持，对大学教学方法改进、教学质量提高和新生录取工作具有十分重要的现实指导意义.

[关键词]研究生成绩； Poisson回归模型； Lasso； 方差分析

1引言

国内各大高校都在推进校园建设的数字化和信息化.在各高校的研究生培养过程中，均已使用较为完善的学生信息管理系统.大量的研究生数据经过日积月累，形成了宝贵的信息资源.然而，在日常行政管理中，这些数据仅用于简单的查询和统计，其所蕴含的内在信息没有得到妥善的发掘和利用.其中影响研究生入学成绩、课程成绩的相关因素尤为值得关注，确定这些影响因素，制定适当的激励政策、教学模式，可以有效提升教学管理质量.

目前国内外对学生成绩数据有广泛的研究.吴兆奇等人利用Logistic回归模型分析学生成绩，并探索其中的关键影响因素[1]；闫在在等人利用Probit模型分析学生补考率影响因素[2]；俞福能通过多元线性回归分析法，根据学生专业课成绩与基础课成绩的相关性，建立了回归方程，进行定量分析[3]；杨淑菊利用主成分分析法分析每个学生成绩的影响主成分和综合得分[4]；Angeline利用Apriori算法分析学生学业表现与出勤率、作业完成情况等因素之间的关联规则[5]；Pandey等人利用决策树算法分析并预测学生学业表现[6].

本文首先通过方差分析对某大学研究生院三年的研究生报名、录取数据进行研究，探究影响研究生入学成绩的因素.然后利用Poisson回归模型分析各个属性变量及入学成绩对研究生课程成绩的影响，并结合Lasso方法对自变量加以选择和系数估计，根据回归系数分析研究生课程成绩的影响因素，从而为研究生院的招生工作提供了数据支持.

2Poisson回归模型及Lasso变量选择

2.1Poisson回归模型

高校信息管理系统中包含大量离散变量，比如研究生所属院系、本科毕业院校类别、录取类别等.在分析这类属性与其他变量之间的关联时，往往会产生计数数据(count data)，即取值为自然数的随机变量，用来表示某种属性类型出现的次数.在高校数据中，同一属性下不同类型的计数值相差不会很大，即其计数数据不会“过度分散”(overdispersed)，因此本文采用Poisson分布作为研究生信息数据属性计数变量的标准模型，并在此基础上建立Poisson回归模型[7].

一般地，假设随机变量Y表示某一事件发生的次数，且服从期望为μ的Poisson分布，则

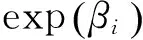
本文将研究生所修的优秀课程数(课程成绩高于90分)记为因变量Y，将研究生入学考试成绩、本科毕业院校类别、培养方式等可能影响研究生学业成绩的因素作为自变量，经过数据整合，可分别拟合出Poisson回归模型，并通过分析自变量系数，探究各因素对学业成绩的影响程度.

在选取作为自变量的因素中，除入学考试成绩是连续变量以外，其余自变量多为离散变量，比如本科毕业院校类别、培养方式等.此类因素一般可取多个离散值，不易直接加以回归分析，故引进虚拟变量.设一个离散自变量可取k个不同的值，则可以引入k-1个虚拟变量，每个虚拟变量分别用0或1表示此样本是否属于某一类别，若全部k-1个虚拟变量均为0，则表示该样本属于第k个类别[9].

由于大量虚拟变量的引入，同时根据本文方差分析的结果，诸如本科毕业院校类别、培养方式等自变量与同为自变量的入学成绩有显著关联，这将导致普通的最小二乘法或极大化似然函数法估计参数不稳定，因此本文引入Lasso进行Poisson回归模型的变量选择，并估计自变量系数[10].

2.2Poisson回归模型Lasso变量选择在Poisson模型中的应用

基于Lasso变量选择的Poisson回归模型方法，在极大化似然函数的过程中，引入惩罚项，要求系数向量β的l1范数不超过某一个参数λ.这个最优化过程的等价形式是

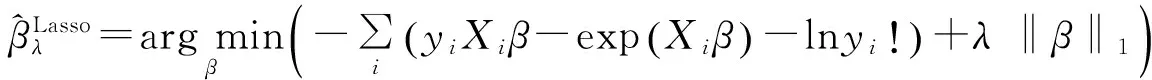
上述公式中参数λ的最优值可以通过交叉检验的方式确定.本文将选择交叉检验中使得回归预测值的标准误差最小的λ作为最终参数，并根据该参数下自变量系数的估计值，分析各自变量因素对研究生学业成绩的促进或削弱作用.利用R语言glmnet包实现Poisson回归、Lasso变量选择以及交叉检验的过程[11].

3数据分析

3.1数据预处理与研究生入学分数影响因素分析

数据来自某大学2011-2013年研究生院三年研究生报名、录取和课程信息数据库，共5384条学生数据，通过对原始数据进行集成、规范、清理、补遗和转化，建立了录取学院、入学考试成绩、培养方式、优秀课程数等30个字段.首先利用方差分析来探究研究生入学分数的影响因素：若在某因素的不同水平下，研究生入学分数呈现显著差异，则说明该因素是影响研究生入学分数的重要因素.由于各年度、各学院乃至各个专业的录取分数标准有所不同，本文通过Z-变换对研究生入学分数加以标准化，使各年度、各专业研究生标准化录取分数均服从标准正态分布，从而消除了录取标准不同的影响.通过对录取研究生信息原始数据中的字段进行初步筛选，最终对性别(包括男、女等2个属性值)、录取类别(包括定向、非定向、自筹、委培等4个属性值)、报考年龄段(包括22岁以下、22到25岁之间、25岁以上等3个属性值)、毕业院校类别(包括985院校、211研究生院校、211非研究生院校、一本院校、二本院校、三本院校以及本校7个属性值)、是否应届(包括应届、非应届等2个属性值)等5项因素加以方差分析.

利用R语言中的Bartlett检验函数对性别因素进行方差齐性检验，结果如表1所示：p值为0.2393，大于0.05，故接受方差齐性假设.在此基础上，利用R语言中的方差分析函数(aov)对研究生录取分数进行关于性别的单因素方差分析，结果如表2所示.

表1　性别因素方差齐性检验表

表2　性别因素方差分析表

由表2可知，关于性别的方差分析p值为0.6443，大于0.05，故应接受原假设，即不同性别之间研究生录取分数无显著差异.因此性别不是影响研究生录取的主要因素.而对研究生录取分数进行关于录取类别的单因素方差分析的结果如表3所示.

表3　录取类别因素方差分析表

由表3可知录取类别因素对应的p值为7.0266e-95，故应拒绝原假设，即不同录取类别之间研究生录取分数具有显著差异.因此录取类别是影响研究生录取的主要因素.同样，研究生的本科毕业院校类别和报考年龄段属性对研究生入学成绩有显著影响，其p值分别为8.9623e-05和3.6811e-05.而是否应届对研究生入学成绩无显著影响， p值为0.2875.综合上述分析结果，研究生入学成绩的影响因素为录取类别、本科毕业院校类别、报考年龄.

3.2研究生学业成绩的Poisson回归分析

由于各学院课程设置各有不同，本文以数理学院的数据为例.数理学院研究生三年入学、课程数据，共202条记录.将研究生完成学业任务后的优秀课程数(课程成绩高于90分) 作为因变量Y，将研究生入学考试成绩、本科毕业院校类别、培养方式等可能影响研究生学业成绩的因素作为自变量，引入包含虚拟变量与Lasso变量选择的Poisson回归模型，并估计各入选自变量的系数，从而分析其对研究生学业成绩造成的影响.借助R语言glmnet包中的函数cv.glmnet(X,y,family=”poisson”)，通过交叉检验得到最优化结果，最终Poisson回归模型的入选自变量如表4所示.

表4　Poisson回归模型入选自变量表

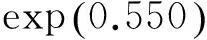
4结论

本文通过方差分析与结合Lasso变量选择的Poisson回归分析方法对积累的各类研究生数据进行处理，将隐藏在丰富数据中的宝贵信息揭示出来，对研究生培养水平有启迪意义的.通过分析对研究生入学成绩以及研究生课程成绩的影响因素，可以为学校研究生院工作的开展提供更为科学的依据，达到促进研究生培养的目标明确化、工作科学化，为院系领导的决策提供理论支持，加强学校研究生院建设，促进研究生培养管理.

但是原始数据仍然存在一定的人为因素偏差，比如入学数据中，不同院校入学成绩的评分标准存在较大差异，面试过程中考官的严格程度各有不同；课程数据中，任课教师的授课态度、课程是否必修均会影响最终成绩对研究生水平的反映等，同时高校原始数据的丰富性、多样性和准确性仍有待加强.应根据院系间、师生间的沟通与反馈，建立科学合理的质量评价体系，广泛收集优质、准确、关联性强的研究生入学及培养数据，为更扎实合理的数据分析和挖掘打下基础.

[参考文献]

[1]吴兆奇, 关蓬莱, 吴晓明. 考试成绩的LOGISTIC回归模型研究[J]. 统计与决策, 2007(5): 21-23.

[2]闫在在, 郑丽霞, 赖俊峰，等. 基于Probit模型的学生补考率影响因素分析[J]. 大学数学, 2013, 29(5): 134-137.

[3]俞能福. 多元线性回归在分析学生成绩相关性中的应用[J]. 大学数学, 2007, 23(2): 42-46.

[4]杨淑菊. 主成分分析法在学生成绩评价中的应用[J]. 数学的实践与认识, 2012, 42(16): 131-133.

[5]Angeline D M D. Association Rule Generation for Student Performance Analysis using Apriori Algorithm[J]. The SIJ Transactions on Computer Science Engineering & its Applications, 2013, 1(1):12-16.

[6]Pandey M, Sharma V K. A Decision Tree Algorithm Pertaining to the Student Performance Analysis and Prediction[J]. International Journal of Computer Applications, 2013, 61(13):1-5.

[7]张尧庭. 线性模型与广义线性模型[J]. 统计教育, 1995 (4): 18-23.

[8]郭志刚, 巫锡炜. 泊松回归在生育率研究中的应用[J]. 中国人口科学, 2006 (4): 2-15.

[9]陈希孺. 广义线性模型(一)[J]. 数理统计与管理, 2002, 21(5): 54-61.

[10]Hossain, S., Ahmed, E. Shrinkage and penalty estimators of a Poisson regression model [J]. Australian and New Zealand Journal of Statistics, 2012, 54(3): 359-373.

[11]Friedman, J., Hastie, T., Tibshirani, R. Regularization paths for generalized linear models via coordinate descent [J]. Journal of statistical software, 2010, 33(1): 1-22.

Application of Poisson Regression Model Variable Selection with Lasso in the Graduates’ Score Analyses

AIDong-mei1，HUANGRuo-cheng1，LIANGXiao-yi1，NINGXiao-jun2

(1. School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China;2. Graduate School, University of Science and Technology Beijing, Beijing 100083, China)

Abstract:Research of the main factors affecting the students’ score is a very important part of the students achievement evaluation system. If the several factors which include enrollment category, university category, gender have a significant influence on graduates’ entrance exam score were studied by ANOVA in this paper. Quantitative analysis of the correlation between the discrete variables, admission scores and course scores were analyzed by Poisson regression with Lasso approach, which provides data support for graduate school enrollment work.

Key words:graduates’ score; Poisson regression model; Lasso; analysis of variance

[收稿日期]2015-11-27

[基金项目]北京科技大学研究生教育发展基金项目 艾冬梅(1968-)，女，博士，高工，从事数学建模、数学教学改革等研究.Email:aidongmei@sina.com

[中图分类号]O211.3

[文献标识码]B

[文章编号]1672-1454(2016)02-0030-05