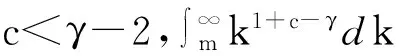具有非线性感染力的一类SIR传染病模型的阈值分析

尹礼寿

(太原工业学院理学系, 太原030008)



具有非线性感染力的一类SIR传染病模型的阈值分析

尹礼寿

(太原工业学院理学系, 太原030008)

[摘要]文章针对一类SIR传染病模型进行了改进，考虑了非线性感染力对阈值的影响.主要分四种情形对非线性感染力下的传染病阈值进行了计算与分析.对结果分析可知，传染病的传播阈值与非线性感染力有着密切关系，同时，免疫率μ对传染病阈值λc也起着非常关键的决定性作用.

[关键词]非线性感染力； 传播阈值； 稳定性

1引言

随着对传染病动力学行为研究的发展，发生在复杂网络中的动力学传播行为也成为一个热点问题.目前广泛研究的模型有SIS，SIR，SEIR等，已经取得了许多实用价值很高的研究成果.在对传染病阈值的分析计算中，大多数传染病模型都假设节点的感染力等于节点的度，节点的度越大，感染其它节点的概率就越大，但在文献[1-5]中指出，有些疾病的传播机制是与这种假设是不符合的(比如性疾病)，一个染病的个体节点可能拥有较多的邻居节点，但在单位时间内其不可能与其所有的邻居节点进行接触.因此，文献[1-5]中提出了非线性感染力.

2模型介绍

对于复杂网络，平均度〈k〉不再是网络的特征表示，为了刻画网络的拓扑结构对传播的影响，在复杂网络中，将节点按度分为不同的组Sk(t),Ik(t),Rk(t)，各组中节点具有相同的度，Sk(t),Ik(t),Rk(t)分别代表在时刻t度为k的易感节点、感染节点、免疫节点的密度.本文主要在文献[1]得到的结论启示下，考虑了免疫率μ对模型的影响，进行改进后得到的模型如下

(1)

模型中，ω>0代表免疫失效率，感染率为λ，以及个体的免疫率μ.θ(t)代表的是网络中任意一个连接指向一个感染者个体的概率.对于无尺度网络，其具体表达式为

(2)

(2)式中p(k)代表网络中任意一个节点度为k的概率，φ(k)代表度为k的染病节点的感染力，文献[2-3] 中都假设φ(k)=k，也就是一个染病节点能感染它所有的易感邻居节点.显然，这对有些传染病的传播机制是不相符的，因此，文献[4]采用φ(k)=A，φ(k)=kα(0<α<1)，文献 [5] 中提出了更一般的非线性感染力

φ(k)=akc/(1+bkc)，

其中a>0,b≥0，本文基于文献[7]中提出非线性感染力，分析讨论模型(1)在不同情形下的传染病阈值.

3稳定状态及阈值计算

假设模型(1)中方程式等于零,得模型(1)的线性近似系统为

两式相加求解得

(3)

(4)

为得到关于θ的自适应方程，把(4)式代入(2)式中，求解得

(5)

显然，θ=0是(5)式的一个零解，为得到θ(0≤θ≤1)的非零解，有

(6)

从(6)式求解得阈值

(7)

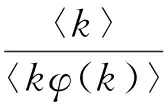
4a,b,c不同取值情形下的阈值计算分析

本节中，假设染病节点具有非线性感染力

其中0≤c≤1，a>0，b≥0.下面对φ(k)式中a,b,c的不同取值情形对传染病阈值造成的影响进行讨论：

(i) 当c=1,b=0时，φ(k)=ak.在此情形下

(iii) 当0

(iv) 当a,b,c≠0时，

在此种情形下

5结论分析

[参考文献]

[1]Liu Jingzhou, Tang yifa, Yang Z R..The spread of disease-with birth and death on networks[J]. Elsevier Science,2008(9):38-49.

[2]Liu J, Zhang T. Epidemic spreading of an SEIRS model in scale-ree networks[J]. Commun. Nonlinear Sci.Numer. Simulat,2011 (16):3375-3384.

[3]Zhang J, Jin Z, The analysis of epidemics network model with infectious force in latent and infected period[J]. Discrete Dynam.Nat.Soc.2010:1-12.

[4]Yang R, et al. Epidemic spreading on heterogeneous networks with identical infectivity[J]. Phys.Lett. A 2007 (364):189-193.

[5]Fu X, et al, Epidemicdynamics on scale-ree networks with piecewise linear infectivity and immunization[J]. Phys.LRev. E ,2008 (77)： 86-113.

[6]Zhang Haifeng, Fu Xinchu，Spreading of epidemics on scale_free networks with nonlinear infectivity[J]. Nonlinear Analysis，2008(02):353-367.

Threshold Analysis of an SIR Epidemic Model with Nonlinear Infectious

YINGLi-Shou

(Taiyuan Institute of Technology, Department of Physiology,Taiyuan 030008, China)

Abstract:Taking into account the effect of nonlinear infectivity on threshold value，this paper has improved a kind of SIR epidemic model. And the threshold for epidemic under the nonlinear infectivity is analyzed respectively according to four cases. From the result, we know that the thre-shold for epidemic is intimately linked with nonlinear infectivity. At the same time, the immunization rate μ has important effects on the threshold for epidemicλc.

Key words:nonlinear infectivity; threshold value; stability

[收稿日期]2015-09-15；[修改日期] 2016-02-16

[基金项目]山西省自然科学基金项目(2012011002-2)；2015年山西省高等学校教学改革项目(118)；山西省教育厅科技研发基金项目(20091041)；太原工业学院理科重点基金项目(2009LZ02)

[作者简介]尹礼寿(1982—)，男，讲师，硕士，从事传染病的数学建模与动力学分析理论研究. Email: 1071864370@qq.com

[中图分类号]O19

[文献标识码]B

[文章编号]1672-1454(2016)02-0022-04