初中数学解题教学策略探究

张谷银

摘要：从近年的教学趋势来看，针对学生数学解题思维的培养已经成为初中数学教学中十分重要的一个环节.数学解题需要以解题教学为平台，通过各种方式引发学生主动对数学解题方式的思考，帮助学生养成创造性的思维模式，从而提高初中数学教学质量.

关键词：初中数学 解题策略

一、研究背景及意义

1.研究背景

目前，有些教师在初中数学教学中对教材理解程度不高，很多时候在课堂上提出的问题和讲解的内容都有所欠缺，使学生对于数学的理解存在误区.有些学生在数学学习过程中完全依靠模仿和死记硬背，对数学概念、性质和思路造成混乱，没有教师的讲解就无法完成学习任务，没有养成主动思考的习惯，遇到任何困难都等待教师来进行讲解，考试中遇到困难就无从下手.因此，让学生通过自己的思考来解决数学问题成为近年来初中数学解题教学中的难点和热点.

2.研究意义及方法

目前，有些教师将大量的精力放在数学教学上，但是很多学生对于数学解题思路的理解还很浅显.针对学生数学解题思维的培养已经成为初中数学教学中十分重要的一个环节.数学解题需要以解题教学为平台，通过各种方式引发学生主动对数学解题方式的思考，帮助学生养成创造性的思维模式，从而提高初中数学教学质量.从现阶段来看，数学解题策略研究已经成为新课标的主要教学目标，培养学生独立解决数学问题具有重要意义，而且数学解题策略相互之间存在一定的联系，能够让学生养成独立自主的学习习惯.笔者主要通过大量的文献阅读及实际教学经验，对初中数学解题研究进行分析总结，为初中数学解题研究作出贡献.

二、国内外数学解题策略研究概述

1.国外数学解题策略研究情况

国外数学解题主要注重于问题的解决，从20世纪80年代开始，欧美国家对于学生数学教学的问题解决能力十分重视，从美国数学教师协会发布的《行动议程》上可以看出，他们将问题解决必须成为数学教学的核心作为第一要务，并且在相应的标准中提出了学生解决问题策略的应用和掌握解题教学的方式.例如，日本提出了将数学教学的所有活动都归纳入问题解决中，德国提出数学教学中需要提高的是学生解决问题的能力和创造力.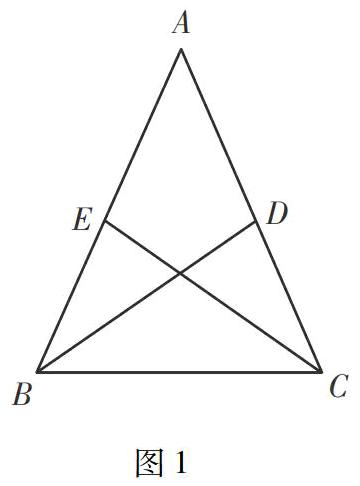

2.国内数学解题策略研究情况

近年来，随着我国教学改革的不断深入，借鉴了一些相应的国外教学经验，对数学课堂教学进行改革，包括了简化课堂教学内容，课时重新安排和训练学生解题能力等.由于受到传统教学思维的限制，目前的整体情况并没有太大的改变，特别是数学教学中，解题能力还没有成为教学的核心思想，仍然将知识点作为主要内容进行教学，这就使我国初中数学解题研究还有很多的不足.

三、数学解题策略案例分析

1.数学解题策略案例分析

从目前的初中数学解题教学来看，一般的解题步骤分为四个步骤：首先是对题意的理解，其次是构建解题计划，再者是根据计划解题，最后是检验.下面通过一个例题进行数学解题策略的分析.

例如，如图1，在△ABC中，AB=AC，BD，DE分别是△ABC的角平分线，求证：BD=CE.

（1）题意理解.本题是证明等腰三角形两底脚的平分线相等，题意的理解要分清楚条件和结论.本题的条件是等腰三角形中两底脚的平分线，结论是两条平分线相等，分析以后，就可以清晰地理解题意.

（2）构建解题计划.对于解题来说，一个合理的解题计划有利于问题的解决.对于学生来说，构建出一个详细的解题计划，能够帮助学生理解知识和培养解题能力.首先要做的就是在图1中标出必要的信息，根据图形和题意确定已知和求证，随后通过分析已知探索证明思路.对于证明题来说，主要有三种思考方式.第一种是正向思考.通过已知条件，分步骤向问题靠近，对于一般题目较为适用.第二种是逆向思考.对于一些条件较为分散的题目，需要从问题入手分析，进行反向思考，如本题，学生可以通过思考，如果两条角平分线相等，学过的相关知识点和证明方法有哪些.例如，全等三角形角平分线相等知识，已知条件是否能够证明该三角形是全等三角形，如果不能证明，还缺少哪些必要条件，这样一步一步找到解题思路，最后把证明过程正着写出来即可.即证明BD=CE，就要引导学生观察图形，弄清题意，发现BD，DE分别存在于两对三角形中，△ABD与△ACE，△BEC与△CDB，那么只要能证明其中任何一对三角形全等，即可利用全等三角形性质得到对应边相等.第三种是正逆结合思考.目前，这种思维在初中数学中应用较少，往往需要学生对题目给出的所有已知条件进行认真分析，看每一个条件都能得出什么.例如，一看到三角形某边中点，马上想到中位线，对于直角三角形，不仅要想到中位线，还要想到斜边中线.

（3）根据计划解题.构建解题思路后，就需要使用数学语言和符号书写出相应的解题过程，证明题在证明过程中需要学生严格按照相关数学语言和符号进行书写，书写的规范十分重要.证明略.

（4）检验.检验是学生常常忽略的一个步骤.对于证明题来说，需要学生对其过程和结论的正确性进行检验，查看整个证明过程是否合理，对于每一个步骤的理论和性质进行检查，如果出现了遗漏和错误，要进行及时纠正.

2.数学思想方法解题案例分析

数学思想方法对学生在数学解题上的作用是举足轻重的，而且应用解题的范围越来越广泛，从而受到教育工作者的关注.

（1）分类思维.初中学生刚接触分类思想，对其含义、作用和影响都一知半解，要求教师在教学中对分类思想的应用进行整理，先在一些概念性的内容中稍稍渗透，让学生对分类思想有一个初步的认识，然后慢慢渗透到证明题、计算题等.这样，不仅在学生思维上起到对分类思想的影响作用，更能够加深学生对数学思想方法渗透的理解和应用.

（2）数形结合.对于一些描述题目来说，将现有的数与形两部分结合在一起，能够形助数和以数解形，能使较复杂的问题简化的一目了然，抽象的问题建立起直观的形象，是解决数学问题的一种重要的思想方法.

总之，在新改革的大环境下，在数学教学中，培养学生的解题思维和对解题教学的重新布局是教学重点.数学解题策略是初中数学教学的核心，让学生熟练地掌握解题技巧和培养学生的解题思维是初中数学教师的主要工作.教师需要将解题技巧和解题思维同目前的教育方式结合起来，让学生在获得知识的同时能够学会如何解题，让学生学会独立思考问题，而不是依靠教师的讲解.教师要根据初中生的学习特点制定相应的教学计划，将数学解题策略融入到自己的教学计划中，同时培养学生的自信心、阅读理解能力和数学语言能力.

参考文献

宋蓓.初中数学解题策略的研究及应用[D].天津师范大学，2013.